1 Introduction

In recent years, the number of wind turbines for energy generation has steadily increased. In order to maintain grid stability, wind turbines must contribute to grid support. Grid operators have defined certain rules and requirements in form of grid codes, to which a wind turbine must comply with to be eligible for grid connection [1]. Nearly all grid codes and standards like [2, 3] require that wind turbines do not disconnect from the grid for a defined period in the event of a fault. This so-called under-voltage ride through (UVRT) requirement means that in the event of a voltage dip, the wind turbine (like any decentralized generation unit) must support the grid by feeding in a reactive current and thus contribute to grid stability [4]. The UVRT tests require different voltage profiles at the point of common coupling (PCC) of the wind turbine, which are produced by voltage sag generators (VSG).

A suitable control algorithm enables the virtual adjustment of the artificial grid impedance at the point of common coupling (PCC) of the device under test (DUT) with the grid simulator of the 4 MW test bench at the Center for Wind Power Drives (CWD) at RWTH Aachen University. A commercial system from the manufacturer Enercon is used to analyze how far the fundamental frequency mapping is sufficient to carry out UVRT tests at different grid parameters. The comparison of the expected and measured resulting voltages shows a high degree of agreement, so that it is assumed that the control of the 50 Hz component of the virtual grid impedance is sufficient for these tests. UVRT tests with deliberately varying grid parameters which are carried out both on the voltage divider-based FRT container and on the grid simulator, lead to different responses of the FVA nacelle research plant. It is recommended to perform UVRT tests on the test bench with predefined grid parameters.

2 UVRT tests

This chapter first describes the two different voltage sag generators (VSG) that are used to perform UVRT tests. Then it presents an overview of relevant standards and technical guidelines. The last part of the chapter describes the test setup at the 4 MW system level test bench of CWD at RWTH Aachen University and the measurement system together with its uncertainties.

2.1 Voltage sag generator

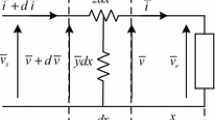
The state of the art test facility for UVRT tests is the shunt impedance based VSG (often called FRT container), based on the principle of a passive voltage divider. It is connected between the PCC of the wind turbine and the public grid. Fig. 1 shows a simplified representation of the shunt impedance based testing equipment. Various literature such as [5,6,7] explain the principle and operation of this equipment.

Fig. 1
figure 1

Shunt impedance based VSG. (According to [3])

Full size image

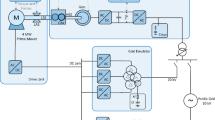
A converter system representing an actively controlled voltage source is an alternative VSG for UVRT tests. This technology is usually used on test benches to generate voltage sags. Fig. 2 shows the simplified diagram of the grid simulator installed at the center for wind power drives (CWD) at RWTH Aachen University [8, 9].

Fig. 2
figure 2

Simplified representation of the grid simulator installed at CWD at RWTH Aachen University [8]

Full size image

2.2 Certification with focus on UVRT tests

The international standard IEC 61400-21‑1 describes a uniform methodology for determining the electrical properties of grid-connected wind turbines. It gives recommendations on the procedure to take measurements and evaluate the electrical properties of grid-connected wind turbines. The technical guidelines of the German ‘Fördergesellschaft Windenergieanlagen und andere dezentrale Energien’ (FGW) are based upon the IEC 61400-21 series and national grid codes. They are the relevant guidelines for the certification of wind turbines in Germany. The FGW TR3 is the part which refers to the electrical properties of grid-connected wind turbines.

According to IEC 61400-21‑1 UVRT tests can be carried out either using a voltage divider or a suitable grid simulator. During UVRT events, the VSG must comply with the voltage curve in Fig. 3 as long as the wind turbine is disconnected or in no-load condition [2]. The grid short circuit power needs to be at least three times the nominal apparent power of the DUT and an X/R ratio of at least three is required at the PCC of the DUT [3]. Generation plants are obliged to feed a reactive current into the grid in order to support the system voltage in case of faults. The additional reactive current \(\Updelta i_{B}\) of the generation unit during faults is proportional to the voltage deviation \(\Updelta u\). The gain factor \(k\), adjustable between 2 and 6, specifies this relationship [10].

$$\Updelta i_{B}=k\cdot \Updelta u$$
(1)
Fig. 3
figure 3

Positive sequence voltage and tolerances of an UVRT test [2]

Full size image

2.3 Test setup

Fig. 4 shows the structure of the experimental setup. A detailed description of the test bench setup is given in [9, 11]. The transformer provides two taps on the high voltage side, which enable to connect the DUT either to the converter based grid simulator of the test bench with 20 kV nominal voltage or to the public grid with 10 kV nominal voltage. In order to carry out UVRT tests on the public grid, a shunt impedance based VSG (also called FRT container) is connected between the transformer of the DUT and the public grid. The DUT is in the first case the research FVA nacelle [8]. It is used to perform comparative measurements between the shunt impedance based VSG and the grid simulator at the test bench. For this purpose the FVA nacelle is connected to the drive unit of the test bed, consisting of the 4 MW direct drive and a mechanical load application unit (LAS). Initially, UVRT tests are carried out on the grid simulator, followed by similar tests on the public grid, where a voltage divider-based VSG is used to perform the tests. This approach enables the investigation of the grid parameters influence and the artificial grid mapping, since all deviations in the results can be caused solely by the electrical system. Table 1 shows the values for the series impedance Z1 and the short-circuit impedance Z2 of the shunt impedance based VSG for different voltage depths.

Fig. 4
figure 4

Test setup with shunt impedance based UVRT testing equipment and grid simulator [11]

Full size image
Table 1 Impedances for the voltage divider based UVRT container
Full size table

The second DUT is the commercial wind turbine E‑115 E2 from Enercon. It is also connected to the drive unit of the test bench. All UVRT tests with the E‑115 E2 are performed on the grid simulator. It demonstrates the properties of the grid simulator for virtual impedance matching. As this is a commercial wind turbine, the reactive current setting and the behavior during grid faults are already certified. This ensures that any deviating behavior is caused by the grid impedance emulation of the grid simulator, not by the DUT. Table 2 shows the key parameters of both nacelles.

Table 2 Key parameters of the two DUTs
Full size table

2.4 Influence of wind turbine reactive current on PCC voltage

There is a strong correlation between grid parameters and the influence of the reactive current injection by the wind turbine on the system voltage at the PCC. The stronger a grid, i.e. the higher the difference between the rated power of the plant and the PCC short-circuit power, the greater the voltage support provided by the injected reactive current. The voltage-supporting effect also depends on the \(X/R\) ratio of the grid impedance. The more inductive a grid, the stronger the voltage increase due to the capacitive reactive current injected [12]. In contrast to the shunt impedance based FRT containers used for field tests, grid simulators offer the possibility to vary the short-circuit power as well as the \(X/R\) ratio at the PCC. Since the steady-state PCC short-circuit power \(S_{Sc}\) is calculated from the grid voltage \(V_{G}\) and the grid impedance \(Z_{G}\) at fundamental frequency according to Eq. 2, it can be affected by adding a virtual impedance [13].

$$S_{Sc}=\frac{U_{G}^{2}}{Z_{G}}$$
(2)

3 Grid simulator—impedance control

The grid impedance determines how much the terminal voltage deviates when the wind turbine injects reactive currents into the PCC. A small impedance characterizes a strong grid with low deviations and a big impedance characterizes a weak grid with high deviations. Yet, there is no precise definition of weak and strong. The short-circuit ratio which relates the available grid short-circuit power to the rated turbine power is usually used to express this.

$$SCR=\frac{S_{Sc}}{S_{N}}\;2.5\ldots 6\,\text{ is considered as weak}$$
(3)

Short-circuit power \(S_{sc}\), short-circuit ratio SCR and grid impedance \(Z\) are coherent quantities. They are all expressions for the same inherent grid property which relates current injection to terminal voltage variation and thereby affects the turbine reactive power management.

The grid simulator controls the PCC impedance in order to simulate the voltage response on turbine current injection. Fig. 5a presents the scheme of the test bench with the dedicated controller and its required measurements. Fig. 5b shows the equivalent circuit to which the control references obey.

Fig. 5
figure 5

Grid simulator PCC impedance control. Hardware scheme (a). Equivalent circuit (b)

Full size image

The PCC is supplied by a configurable voltage source in series to a configurable impedance. The virtual voltage drop across the reference impedance \(Z\) is added to the internal voltage reference \(U_{0}\) to generate the appropriate reference for the emulators’ PCC voltage controller.

$$U_{\mathrm{PCC},\mathrm{ref}}=U_{0}+Z\cdot I_{\mathrm{PCC}}$$
(4)

In voltage controller closed loop operation, the fundamental frequency voltage response on injected turbine currents corresponds to the referenced impedance. With this method, basically any fundamental PCC impedance can be simulated — from very strong grids with low impedances \(Z\rightarrow 0\) to very weak grids with high impedances. There are no constraints on \(X/R\) ratio, either inductive or capacitive. Furthermore — although not reasonable — also negative impedances would be possible.

3.1 Verification of the grid impedance setting

The control functionality was validated by measurements where the E‑115 E2 was used to inject defined active and reactive powers into the PCC. As long as the turbine is at no-load the PCC voltage equals the no-load voltage \(U_{0}=20\,\mathrm{kV}\). Given an impedance \(Z\) and an injected PCC power \(S_{\mathrm{PCC}}\) the circuit equation derived from Fig. 5b can be solved for the expected voltage \(U_{\mathrm{PCC}}\) and current \(I_{\mathrm{PCC}}\). That means if the turbine injects the requested power and the measured voltages and currents match the expected values, then the impedance controller operates correctly.

The functionality was tested for three different grid impedance settings 40, 65 and 100 MVA at a constant ratio of \(X/R=50\). For each impedance setting an active power of 1 MW and reactive powers of ±2 Mvar (capacitive and inductive) were given as a reference to the turbine power controller. The power was injected into the low voltage windings of the turbine transformer which has an impedance voltage of 7.5% at 3.5 MVA rated power as presented in [8]. The actual injected PCC power is determined with consideration of the transformer voltage drop and its power consumption. Six PCC operating points have been tested which are presented in Table 3.

  • Table 3 cases 1, 3, 5 — the turbine generates 2.0 Mvar and feeds them into its transformer:

    • The turbine generates reactive power — being capacitive — and the PCC voltage rises.

    • The PCC reactive power is lower than 2.0 Mvar because the transformer consumption partially compensates the turbine generated power.

  • Table 3 cases 2, 4, 6: — the turbine consumes 2.0 Mvar and draws them from its transformer:

    • The turbine consumes reactive power — being inductive — and the PCC voltage falls.

    • The PCC reactive power is higher than 2.0 Mvar because the transformer consumption adds to the turbine consumed power.

Table 3 Impedance verification at PCC for operating points at 50 Hz
Full size table

The low errors in voltages and currents show a good match between measured and expected values. This proves the correct operation of the fundamental frequency impedance control.

Transients are not considered. They contain high frequency components and they depend amongst others upon the impedance controller frequency response which is not in the scope of this paper [13].

3.2 Verification of the grid impedance setting during UVRT tests

Three-phase UVRT tests are performed with the E115-E2 at different impedances of the artificial grid. The short circuit power is changed between 14 MVA and 1000 MVA at a constant X/R ratio of 12.5. Since the voltage dip is balanced, only the positive sequence system needs to be considered. Fig. 6 shows the calculated and measured resulting positive sequence voltage at the PCC. The conversion of the measured phase voltages into the fundamental positive sequence voltage is performed according to [2]. The measured values deviate from the theoretical values by a maximum of 0.6%. It is noticeable that the deviation increases with increasing short-circuit power. This is caused by the unconsidered impedance of the wind turbine connection to the PCC. The proportion of the wind turbine’s connection cable in the total impedance increases with increasing short-circuit power, so that the deviation between specified grid impedance and existing grid impedance increases. The comparison shows that it is sufficient for UVRT tests to specify the 50 Hz component of the artificial grid impedance.

Fig. 6
figure 6

Comparison of the calculated and measured fundamental positive sequence voltage at the PCC

Full size image

4 Influence of the grid parameter

Comparison with field measurements shows that it is possible to reproduce UVRT tests on a system test bench. For this purpose, virtual impedance control is used to simulate the PCC parameters resulting from the combination of the grid impedance and the impedances of the shunt impedance based FRT container to the wind turbine at the test bench [14]. A detailed investigation on comparability of test bench and field measurements at differently adjusted short circuit powers at the PCC is still pending. At CWD there was temporarily the possibility to perform UVRT tests either at the grid simulator or at the FRT container. This setup offers the chance to test the effect of the grid influence at the same mechanical input parameters. It ensures that all deviations are exclusively caused by the electrical system.

Therefore different grid impedances are deliberately set between the two test methods. The grid parameters on the public grid result from the grid impedance at the connection point of the UVRT container and the serial and shunt impedances of the UVRT container. The base impedance Zbase is set on the grid simulator. Table 4 describes the grid parameters of both test facilities. For tests with the UVRT container, the short circuit power at the PCC is calculated with the highest impedance parameter from Table 1. This leads to the lowest short circuit ratio at the PCC which is still higher than the required value of three. The artificial grid has a short circuit ratio of 24, which is significantly larger than required. An X/R ratio of at least three is achieved by both test facilities. Although the UVRT tests are carried out with completely different grid parameters, both are permissible according to the standards [2] and technical guidelines [3].

Table 4 Grid Parameters for both test facilities
Full size table

Especially in the case of two-phase voltage dips, there is a significant discrepancy between the two test methods. This paper compares the two-phase voltage dips to 0.74 pu as an example. Fig. 7 shows the measurement results with the shunt impedance-based VSG above and the behavior on the grid simulator below. Shown is the rms value curve of the fundamental frequency positive sequence voltage (left) and negative sequence voltage (right) at full load operation of the wind turbine. The voltage measurement shows the desired behavior for tests on the grid simulator. The voltage level during the dip is at the expected high level since the voltage dip level equals positive sequence minus negative sequence. Even before the fault, an increase in the PCC positive sequence voltage to 1.03 pu can be noticed. During the fault, the PCC voltage is increased by 0.04 pu compared to the no-load test. The DUT supports the voltage as required by injecting a reactive current. It is noticeable that the negative sequence voltage is identical in the no-load and load cases. From this, it can be concluded that the voltage support takes place exclusively in the positive sequence. An unexpected behavior of the PCC voltage occurs during the two-phase tests with the voltage divider-based test equipment. The voltage increases in a pulse-like manner every 500 ms. The pulse-like change is due to the reactive power support of the DUT. Since the DUT only controls the positive sequence system, the reactive current injection occurs symmetrically in all three phases. The series impedance of the shunt-based VSG results in a high grid impedance and thus a weak grid. In combination with the injected symmetrical reactive current, the voltage in the non-disturbed phases increases to such an extent that the detection threshold for OVRT tests is exceeded. The controller stops the reactive current injection. After a delay time of 500 ms, the DUT again detects a voltage dip and starts symmetrical reactive current injection to support the voltage. It is obvious that the response of the DUT to under voltage events does not correspond to the required behavior. The measurement on the grid simulator, on the other hand, shows that the DUT is capable to handle under voltage events. The requested voltage support is also provided in this case. It is concluded that the different grid parameters not only lead to the expected deviation in the resulting voltage level [12]. Rather, the overall behavior of the DUT differs. For this reason, it is necessary to simulate the public grid characteristics on the grid simulator for comparative measurements.

Fig. 7
figure 7

RMS voltage of the positive (left) and negative (right) sequence voltage for two-phase votlage dips to 0.74 pu for shunt impedance based (above) and converter based (below) VSG

Full size image

5 Conclusion

The grid parameters at the grid connection point of the wind turbine influence the impact of the obligatory reactive current injection on the system voltage in the event of a grid fault. Converter-based grid simulators can specify various artificial short-circuit powers at the PCC. They offer the possibility of carrying out voltage dip tests under various conditions. It is possible to control the fundamental frequency component of the grid impedance on the 4 MW system test bench at the CWD. Tests with a commercial DUT show that the simulation of the 50 Hz component of the grid impedance is important to investigate the influence of different grid parameters during a voltage dip. However, the effects on the transient region of a fault are not considered. Comparative measurements between the grid simulator and an FRT container based on the voltage divider principle with intentionally different grid properties indicate that the grid impedance can influence the overall behaviour of the DUT. For this reason, it is recommended to perform the certification measurements for UVRT tests on test benches with predefined grid parameters.