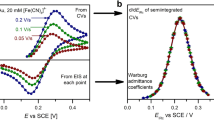
Abstract
With the purpose of fast characterization of electrode reactions, a dynamic electrochemical impedance spectrum (dEIS) measurement system has been assembled which permits the continuous collection of audio-frequency impedance spectra while performing cyclic voltammetry measurements with the usual scan rates of up to 200 mV/s. The performance of this system was tested by analyzing the CV curves and impedance spectra taken simultaneously in ferro-/ferricyanide containing aqueous solutions yielding an experimental demonstration of the connection of the semi-integrated reversible voltammograms and the Warburg coefficients.

Graphical abstract
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
Electrochemical impedance spectroscopy (EIS) is a widely used method of electrochemists; its main role is the determination of rates of interfacial processes. Impedance measurements are usually performed by applying a sinusoidal perturbation of ω frequency upon the potential or current and correlating the ac terms of these two quantities to each other. The Z(ω) impedance spectra are compiled from frequency-by-frequency measurements. Devices needed for this method are commercially available and precise, though the measurement itself can be somewhat time-consuming, especially at low frequencies.
There are a couple of conditions which must prevail for the EIS measurement. The system should be in steady state for the time of the measurement even at the lowermost frequency. This is generally achieved at the “static” EIS measurements, i.e., when the ac perturbation of potential (or current) is applied upon a constant dc potential (or current). Nevertheless, if some properties of the system are slowly changing, then the lowermost frequency should be chosen accordingly. In the same vein, the time of taking the complete spectrum should be minimized. A possible way of making the measurement faster is to use periodic perturbation with a periodic function comprising many harmonics. The signals of the perturbed potential and that of the corresponding current response are Fourier-transformed, and impedance values are calculated for each harmonic component. Since the overall potential perturbation must not exceed a few millivolts to keep the current-voltage relation in a linear range, the phases of the harmonics must be carefully chosen. A random selection of those phase angles is usually acceptable. Such a periodic perturbation function made of dozens (maybe hundreds) of harmonics—preferably odd harmonics of approximately logarithmically equidistant frequencies—with random phases is called a “multisine.” It is worth to be noted that this method has been elaborated almost a half a century ago in various laboratories [1,2,3,4].
The big advantage of a multisine EIS over the traditional sine-after-sine EIS is in its speed. During the time needed for the base harmonic, the complete spectrum is measured— at the expense, obviously, of the accuracy of the spectrum points (for the analysis of the trade-off see [5]). Such an instrument has been assembled recently in our laboratory for testing two-electrode symmetrical cells: for electrochemical double-layer capacitors [6, 7]. This system could measure audio-frequency impedance spectra in a couple of seconds; it yielded the values of a simple, three- to five-element equivalent circuit parameters within this time.
It is worth to combine such a fast EIS measurement with the traditional cyclic voltammetry (CV); such a combination is called dynamic EIS. This method, dEIS, has already a long history, a number of devices have been constructed for the purpose of dEIS, and various electrochemical phenomena were studied either by dEIS or by equivalent methods of different names [8,9,10,11,12,13,14,15] (for a recent review, see, e.g., [16]). Evidently, the scan rate of the CV affects the low frequency limit of the EIS. As a rule of thumb, during one spectrum measurement, the electrode potential should not be changed more than a couple of millivolts. For example, for 100-mV/s scan rates with a 20-Hz low frequency limit, we have one spectrum for every 5 mV; with 50-mV/s scan rate, we can measure down to 10 Hz. In order to filter out the effect of the CV ramp signal, appropriate windowing functions (e.g., of Hanning) should be applied.
The subject of this paper is a dEIS setup, described in Section 3. This was tested with various dummy cells; however, its properties should be demonstrated with real electrochemical cells. To this aim, we chose a well-known, well-defined electrochemical system whose properties are easy to be reproduced: this is the ferro-/ferricyanide redox couple in an aqueous supporting electrolyte. The simultaneous CV and EIS measurements are described in Section 4; by their analysis, we experimentally demonstrate the statement of Refs. [17, 18] that for systems with reversible CVs the potential derivative of the semi-integrated CV equals the Warburg admittance coefficient obtained from dEIS.
Background: CV and EIS of reversible redox systems
The electrochemical system was chosen to comply with the behavior of the theoretical so-called reversible redox systems at planar electrodes as treated in textbooks, like in Ch.6.2. of [19]. Accordingly, the theory of the ideal case considers the following:
-
(a)
An inert metal electrode of an ideally planar surface is immersed in a quiescent electrolyte solution of large volume.
-
(b)
The electrolyte contains a redox system in small concentration in a so-called base (or supporting) electrolyte, that is, which consists of inert ions of high concentration and hence exhibits a high conductivity.
-
(c)
Current is carried by the migration of the supporting electrolyte’s ions in the bulk, whereas it flows across the metal/electrolyte interface via electron transfer associated with the redox system.
-
(d)
The electron transfer across the interface is assumed to be infinitely fast; as a consequence, the concentrations of the redox components are always set by the actual electrode potential.
-
(e)
The concentration of the redox species is uniform throughout the solution at the experiment’s start time.
Due to condition (d), the current is determined by the transport of the redox species to the interface rather than by the charge transfer across the interface. The transport to the interface is governed solely by the laws of diffusion; other forms of transport (convection and migration) can be safely disregarded (cf. conditions (a) and (c)). Due to condition (b), the potential scale is not distorted by an IR drop; and as condition (c) claims, there is no charging current involved, so double-layer charging is out of the scope.
The above textual assumptions are projected onto a mathematical form when we use the Fick equations with one Cartesian coordinate for calculating the concentration map and the Nernst equation as a boundary condition for connecting surface concentration with electrode potential. These equations always apply irrespectively of the actual E(t) potential dependence.
CV and EIS are two archetypes of the measurements characterizing the transient current—electrode potential—the j(t) vs E(t)—relation: these are the large and small-signal responses, respectively. The mathematical forms of these two archetypes—of the diffusional (Warburg) impedance and of the reversible cyclic voltammogram—are well-known (see, e.g., Chs. 9.3. and 6.2 of [19]).
Apart from the difference in the range of the potential excursions, there is another important difference between the Z(ω) impedance function and the j(E) voltammograms. The Z(ω) impedance function is potential program invariant, i.e., it “does not remember” the actual form of the potential perturbation by which it has been measured. In contrast, the j(E) voltammograms depend on the actual E(t) function, e.g., on scan rates and the vertex potentials. However, there exists a procedure by which all reversible voltammograms can be transformed to the one and the same Mrev(E) function—that is, to a state function which depends on the actual E only rather than on the previous E(t) function. This procedure yields the so-called semi-integrated voltammogram, M(t) plotted against E(t), where the M(t) semi-integral is calculated from j(t) by the
convolution [20, 21]. For reversible redox couples, the Mrev(E) is potential program invariant: it exhibits neither scan rate dependence nor hysteresis for CVs of multiple scans. Potential program invariance implies that IR drop–distorted reversible CVs can be transformed into potential program invariant form by correcting the potential scale by the IR drop, i.e., M vs EIRc is plotted where EIRc ≡ E − IR.
As it has been shown in [17], dMrev/dE equals the coefficient of the Warburg admittance, σ, obtained from EIS (the Warburg admittance is defined as YW = σ (iω)1/2 with i and ω being the imaginary unit and the angular frequency, respectively). This is how the large-signal and small-signal response functions (CV and EIS, respectively) are related to each other through their potential program invariant forms. In the present article, we demonstrate experimentally just the same relation of CV and EIS: we measure CVs of a reversible redox system, calculate its dMrev/dE function. Simultaneously, we measure EIS and calculate the Warburg admittance’s coefficient. The two quantities should be equal.
The features of the reversible voltammograms are well-known (see Ch. 6.2 of [19]). Even if the charge transfer is very fast, there are various reasons why we do not get ideal, “textbook-conform” reversible CVs. These main reasons are as follows:
-
(a)
Non-zero solution resistance. It causes a significant IR drop yielding distortion of the CV with the most salient feature that peak separation increases with the scan rate. Fortunately, this is a deviation which can be corrected electronically during the measurement or numerically afterwards—just like in our present case.
-
(b)
Capacitive current charging the double layer. This effect is pronounced at high scan rates because capacitive currents are proportional to the scan rate, whereas the diffusion-controlled currents increase with the square root of the scan rate. Since the double-layer charging depends on many and diverse parameters (among them uncontrollable ones), separation of the diffusional and charging currents is difficult. Perhaps the best way is to measure the reversible CVs with as-high-as-possible redox species concentrations at low scan rates.
-
(c)
Too long measurement time. The diffusion-limited current decays to a level where the transport, due to “spontaneous convections,” gets comparable to it. In other words, the diffusion layer gets scrambled; therefore, transport is somewhat enhanced. This effect appears as increased currents at the tails of the CVs. As a rule of thumb, the diffusion-related experiments should not be longer than 10 s (or so); the scan rate (or the potential range) should be chosen accordingly.
-
(d)
Non-planar electrode geometry. The theory and the demonstration experiment involve planar electrodes. The diffusion layer width during the above-mentioned 10 s is in the order of magnitude of 100 microns. Hence, no curvature smaller than this distance is compatible with the theory. For example, a bended, convex surface would yield enhanced transport—appearing as increased current at the tails of the CV. In contrast, the surface of a 1 mm in diameter cylindrical electrode can be safely regarded to be planar.
The above four conditions often contradict each other. However, it is possible to find appropriate conditions for reversible CVs. In our opinion, the best way to demonstrate the reversible nature of CVs is to present them in M vs E representation (with applying IR correction of the potential, see later). The CVs are reversible ones, if all M vs E plots are hysteresis-free and are the same for all scan rates.
EIS on this system is traditionally measured by setting a dc potential and waiting some time (say, 10 s) for establishing the equilibrium concentrations of the reduced and oxidized species in the electrode’s neighborhood, as determined by the potential according to the Nernst equation. Impedance spectrum is measured with such concentration conditions. Dynamic EIS is measured with continuously scanned potential. Provided that the spectra can be measured in a sufficiently short time during which potential change is little, the spectra do not depend on the scan rate. This is so because the concentration ratio of the reduced and oxidized species is adjusted instantaneously following potential change.
In general, analysis of EIS is usually done by fitting the parameters by the nonlinear least-squares procedure [22] of an appropriate equivalent circuit to the spectrum, using modulus weighting [23]. For charge transfer reactions, the equivalent circuit is the so-called Randles circuit, Rs − (Cdl || (Rct – W)) where Rs, Rct, Cdl, and W are the solution resistance, the charge transfer resistance, the double-layer capacitance, and the diffusional (Warburg) element, respectively. For a sequence of EIS, Rs must be the same; for reversible systems, Rct = 0. Unfortunately, for real systems, the double layer’s impedance is often ill-defined: modelling it by Cdl is an approximation only. It frequently has a more complicated frequency dependence like that of an adsorption impedance or one which can be approximated by a constant phase element. The ill-defined nature of Cdl can make the determination of the parallelly connected σ parameter of W distorted—with no apparent indication in the output of the fit procedure (χ2 value, parameter errors or covariance matrix). We use the heuristic criterion to accept the fit results only if the impedance of the Warburg term is tenfold smaller than that of the Cdl at low frequencies—in other words, the dominant term of the equivalent circuit is W.
Experimental
The electronics and software needed for dEIS
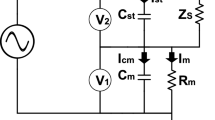
For performing dEIS, a potentiostat is needed with two inputs for two program voltages, one for scanning the dc term of the potential and another for the multisine signal. In the similar vein, also the outputs are doubled: two outputs are needed for the voltages representing dc potential, Edc, and current, Idc, and another two outputs for those of ac potential, Eac, and current, Iac. The block diagram of such a potentiostat is shown in Fig. 1.
Simplified scheme of the potentiostat with the cell containing working, counter, and reference electrodes (WE, CE, RE, respectively). The role of the operational amplifiers OA0 to OA2 are the same as those in a usual adder potentiostat (cf Fig.13.4.5 of [19]). The instrumentation amplifiers IA1 and IA2 are of the same high-pass transfer functions (ac amplification of 100 and cutoff frequency of 5 Hz); they deliver the ac voltages whose ratio is Z(ω)/Rm,ac (the value of Rm,ac is approximately the same as that of the electrolyte resistance between WE and RE). For other abbreviations and details see the text
The perturbation signal contains only certain harmonics of a base frequency; all these harmonics are of equal amplitudes and of random phases. The base frequency has been chosen to adhere to sampling rate, fs = 50 kHz (or sampling time, ∆t ≡ 1/fs), of the four-input AD converter, ADC. As we use Fourier-transform to process the harmonic signals, it is practical to collect 2N data-point arrays permitting the implementation of the fast Fourier transform (FFT) algorithm [24]. In our measurements, N can be chosen 12 to 14, i.e., arrays of 4096 ≤ 2N ≤ 16,384 data-points are taken. To get sharp spectrum lines, the period length of the base harmonic of frequency f0 must match the time of the 2N data-points; hence, the low frequency limit is f0 = fs/2N. The high frequency limit, according to the Nyquist criterion, is fs/2. Finally, we chose only the odd, prime number harmonics (3, 5, 7 etc.) to be included in the multisine signal; the highest frequency was somewhat less than the Nyquist frequency, ≈ 0.7 × fs/2. Actually, for the CV of 100-mV/s scan rate in Fig. 3a, the characteristic data were N = 13, fmin = 3 × f0 = 18.3 Hz, fmax = 0.67 × fs/2 = 17.8 kHz, with 39 frequencies in a spectrum (from the 3rd to the 2927th harmonics) chosen in a way that they are approximately logarithmically equidistant. Since the period time of the base harmonic is 1/(2N fs) = 163.8 ms, the potential difference of two neighboring spectra is 16.38 mV. This is somewhat more than the value set by our thumb’s rule (vide supra), but our preliminary measurements with decreased Ns hence with larger potential resolution but narrower frequency range gave essentially the same results for this system.
The multisine voltage signal has been generated with a somewhat larger temporal resolution than the digitization: it was calculated with as an array of 5 × 2N length which was converted to voltage with 250-kHz frequency with a 16-bit DA converter. This yielded an ac signal of 0.3-V rms amplitude which has been smoothed with a third-order RLC low-pass filter having a cutoff frequency of 10 kHz. This voltage signal is added to the program voltage with an attenuation of factor 100. The other source of the program voltage is the unattenuated voltage of a PAR-175 analog scan generator.
The four output voltages (denoted as Iac, Eac, Idc, Edc) were digitized by a 16-bit analog-to-digital converter (ADC), the sampling rate of which on its four inputs was fs = 50 kHz. During the 5–100-s-long measurement, these voltages are saved in binary arrays; just afterwards, these arrays are split to shorter ones of 2N length—these are processed further as follows: CVs are generated from the arrays of Idc and Edc; impedance spectra are calculated from the short arrays of Iac and Eac ac voltages. First, the 2N length arrays are Fourier-transformed using the Hanning window. Then, the Z(ω) impedances are calculated from the Fourier coefficients—based on that, the ratio of the complex amplitudes of sinusoidal voltages of frequency ω is Eac(ω)/Iac(ω) = Z(ω)/Rm,ac. Note that there exists an exactly 4-μs time delay between the sampling of Eac and Iac. This delay was taken into consideration and corrected during the calculations.
The data acquisition units (containing both the DAC and the ADC) have been assembled in our laboratory; its full control and data readout are carried out by a PC via its USB interface by a program written in C++. Some parts of the data processing (conversion of the binary readout of the digitizer and the FFT) are done by C++ subprograms called from a VBA program (“Excel macro”). This macro performs the subsequent calculations including the curve fitting (nonlinear least means squares minimization using modulus weighting [23]), plotting, and documenting. A separate subprogram manages the data acquisition for the CV. The complete calculation—including FFTs, impedance calculations, and curve fitting to extract the Randles circuit parameters—requires a couple of seconds following a measurement. The whole measurement and the subsequent analysis are carried out upon a single mouseclick.
The experimental conditions
The electrochemical system was chosen with a view to simplicity: we used a standard, non-thermostated, three-electrode glass cell with gold working, platinum counter, and saturated calomel reference electrodes (WE, CE, and RE in Fig. 1). To minimize charging currents, following La Mantia et al.’s advice [13], 0.5-M KF aqueous solution served as a base electrolyte, which contained 21.3 mM K4Fe(CN)6; it was deoxygenated by high purity (5 N) argon bubbling. The gold working electrode of area 0.316 cm2 was a wire of 1 mm diameter whose end of 1 cm was immersed in the electrolyte. Prior to immersion, the gold wire was cleaned by concentrated nitric acid and also by annealing in a propane gas flame; the exact length of the immersed wire was set by a piece of a thin Teflon tube pulled onto the wire after annealing.
The experiment
Three sets of impedance spectra were recorded in conjunction with CVs of 200, 100, and 50 mV/s between the limits 0 and 500 mV vs SCE, as shown in Fig. 2. The impedance spectra were recorded at instances marked by the dots along the CVs. Two features of the CVs are remarkable: (i) Peak separation is much larger than 59 mV and is increasing with scan rate; (ii) The current does not exhibit any jump at the positive turning point; i.e., the capacitive current is negligibly small even with the largest scan rate.
The semi-integrated CVs are shown in Fig. 3a. Note that the plateau heights are just the same for the three CVs. This is an indication that the current is purely diffusion-controlled at the positive end of the curve. In contrast, the plateaus of the semi-integrated CVs taken with lower scan rates (not shown) are tilted and exhibit hysteresis (most probably because at these low scan rates the diffusion-limited current is so little as to make spontaneous convections also a significant transport mechanism).
a The semi-integrated CVs of Fig. 2. b The same as a, but the potential scale has been corrected for the IR error. The derivative with respect to the IR-corrected potential is also plotted
The semi-integrated CV of Fig. 3a exhibits hysteresis around the redox peaks—this hysteresis is just of the same origin as the increased peak separation on the CVs. Both are due to the IR drop, as it can be demonstrated as follows: From the simultaneous EIS measurements, Rs = 20.3 ohm (or, normalized by the area, 6.32 ohm cm2). Re-plotting the semi-integrated CV with IR drop–corrected potential scale (i.e., M vs EIRc), the hysteresis in the redox peak region disappears; the dM/dEIRc vs EIRc curves for the forward and backward scans coincide (Fig. 3b).
The impedance spectra were analyzed as follows:
Because of the reversibility, we expect identical spectra at the same EIRc potentials. We show spectra in Fig. 4a which were taken approximately at the same potentials (around 0.2 and 0.3 V, in the redox peak region) during scans of three different scan rates, both at positive and negative scan directions. These twice six spectra appear to be quite similar, demonstrating that the scan rate and direction of the scan do not affect the dEIS results.
a Impedance spectra taken during scans of both positive and negative directions, with all three scan rates (200,100, and 50 mV/s). Circles and diamonds are spectra taken at EIRc = 200 ± 8 mV and EIRc = 300 ± 8 mV, respectively. Full and open symbols are for magnitudes and phase angles, respectively. b Warburg admittance coefficient, σ, vs IR-corrected potential, EIRc, as evaluated from dEIS. The solid lines are the dM/dEIRc curves (same as those in Fig. 3b)
All spectra have been analyzed by fitting the parameters of a Randles circuit to the measured spectra; good fits, however, were obtained at the redox peak region (crosses on Fig. 2 mark the IR-corrected potentials at which the spectra could be well fitted to the complete Randles circuit). At these potentials, the σ coefficient of the Warburg admittance could be determined with little error; σ vs EIRc plot is shown in Fig. 4b. In the same plot, with the same scale, dM/dEIRc—the same function as in Fig. 3b—is also shown as solid lines. As this solid lines and the σ(EIRc) points run together fairly well, we conclude that this measurement serves as a good illustration for the following statement: For reversible redox systems, dEIS give two potential functions: one is the dMrev/dE (calculated from the CV) and the other is the σ coefficient of the Warburg admittance (as calculated from the impedance spectra). These are equal to each other.
Conclusions
-
1.
Based on simple potentiostat design principles and electronic circuits, employing data acquisition boards of 16-bit resolution and a few microsecond time resolution, it is possible to build dEIS setups by which series of audio-frequency impedance spectra can be measured, one in every 300 ms. This way, impedance and CV measurements can be simultaneously performed.
-
2.
Such a setup must be validated, not only by dummy cells, but also with well-known electrochemical systems. Perhaps the best for this purpose is a noble metal electrode immersed in some highly conducting aqueous solution containing ferro-/ferricyanide as a minor component.
-
3.
The CV and the impedance behavior of this electrochemical system, in the potential region of the redox peaks, are to be measured and analyzed in that way as described. A dEIS system is of acceptable quality if the plots of dM/dEIRc vs EIRc and σ vs EIRc coincide just as in Fig. 4b.
-
4.
In accord with the theory of [17], the experiment of the present paper demonstrates the connection of CVs and impedances of systems with diffusion-controlled charge transfer through their semi-integrated form of the former and the Warburg coefficient involved in the latter.
References
Creason SC, Smith DE (1972) Fourier transform Faradaic admittance measurements: I. Demonstration of the applicability of random and pseudo-random noise as applied potential signals. J Electroanal Chem Interf Electrochem 36:A1
Blanc G, Epelboin I, Gabrielli C, Keddam M (1975) Measurement of the electrode impedance in a wide frequency range using a pseudo-random noise. Electrochim Acta 20(8):599–601
Pospíšil L, Štefl M (1983) The application of microprocessors in electrochemistry. Collect. Czech. Chem. Commun. 48(5):1241–1256
Nyikos L, Pajkossy T (1986) Electrochemical impedance measurements using Fourier transform (Elektrokémiai impedanciamérés Fourier transzformációval). Magyar Kémikusok Lapja XL:550 (in Hungarian)
Gabrielli C, Huet F, Keddam M, Lizee JF (1982) Measurement time versus accuracy trade-off analyzed for electrochemical impedance measurements by means of sine, white noise and step signals. J Electroanal Chem 138(1):201–208
Pajkossy T, Mészáros G, Felhősi I, Marek T, Nyikos L (2017) A multisine perturbation EIS system for characterization of carbon nanotube layers. Bulgarian Chem Comm 49C:114–118
Felhősi I, Keresztes Z, Marek T, Pajkossy T (2020) Properties of electrochemical double-layer capacitors with carbon-nanotubes-on-carbon-fiber-felt electrodes. Electrochim Acta 334:135548
Házi J, Elton DM, Czerwinski WA, Schiewe J, Vincente-Beckett VA, Bond AM (1997) J Electroanal Chem 499:48
Sacci L, Harrington DA (2009) Dynamic electrochemical impedance spectroscopy. ECS Transactions 19:31–42
Ragoisha GA, Bondarenko AS (2005) Potentiodynamic electrochemical impedance spectroscopy. Electrochim Acta 50(7-8):1553–1563
Darowicki K, Slepski P (2003) Dynamic electrochemical impedance spectroscopy of the first order electrode reaction. J Electroanal Chem 547(1):1–8
Emery SB, Hubbley JL, Roy D (2005) Time resolved impedance spectroscopy as a probe of electrochemical kinetics: the ferro/ferricyanide redox reaction in the presence of anion adsorption on thin film gold. Electrochim Acta 50(28):5659–5672
Koster D, Du G, Battistel A, La Mantia F (2017) Dynamic impedance spectroscopy using dynamic multifrequency analysis: a theoretical and experimental investigation. Electrochim Acta 246:553–563
Tymoczko J, Colic V, Bandarenka AS, Schuhmann W (2015) Detection of 2D phase transitions at the electrode/electrolyte interface using electrochemical impedance spectroscopy. Surf Sci 631:81–87
Macía LF, Petrova M, Hubin A (2015) ORP-EIS to study the time evolution of the [Fe(CN)6]3-/[Fe(CN)6]4- reaction due to adsorption at the electrochemical interface. J Electroanal Chem 737:46–53
Bandarenka AS (2013) Exploring the interfaces between metal electrodes and aqueous electrolytes with electrochemical impedance spectroscopy. Analyst 138(19):5540–5554
Pajkossy T (1997) Potential program invariant representation of voltammetric measurement results of reversible redox couples. J Electroanal Chem 422(1-2):13–19
Pajkossy T, Vesztergom S (2019) Analysis of voltammograms of quasi-reversible redox systems: transformation to potential program invariant form. Electrochim Acta 297:1121–1129
Bard AJ, Faulkner LR (1980) Electrochemical methods. Wiley, New York
Oldham KB (1972) A signal-independent electroanalytical method. Anal Chem 44(1):196–198
Oldham KB, Myland JC, Bond AM (2012) Electrochemical science and technology: fundamentals and applications. Wiley ISBN 978-0-470-71085-2, Ch.12
Bevington PR, Robinson DK (2003) Data reduction and error analysis for the physical sciences, 3d edn. McGrawHill ISBN-10: 0072472278, Ch.6
Boukamp BA (1986) A nonlinear least squares fit procedure for analysis of immittance data of electrochemical systems. Solid State Ionics 20(1):31–44
Cooley JW, Tukey JW (1965) An algorithm for the machine calculation of complex Fourier series. Math Comp 19(90):297
Funding
Open access funding provided by Research Centre for Natural Sciences. The research within project No. VEKOP-2.3.2-16-2017-00013 was supported by the European Union and the State of Hungary, co-financed by the European Regional Development Fund. Financial assistance of the National Research, Development and Innovation Office through the project OTKA-NN-112034 is acknowledged.
Author information
Authors and Affiliations
Corresponding author
Additional information
This paper is dedicated to Fritz Scholz on the occasion of his 65th birthday, to express our high respect towards his contribution to electrochemistry and dissemination of its concepts.
Publisher’s note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Pajkossy, T., Mészáros, G. Connection of CVs and impedance spectra of reversible redox systems, as used for the validation of a dynamic electrochemical impedance spectrum measurement system. J Solid State Electrochem 24, 2883–2889 (2020). https://doi.org/10.1007/s10008-020-04661-8
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10008-020-04661-8