Fifty years of studies of double layer effects in electrode kinetics—a personal view

Abstract

Developments in the treatment of double layer effects in electrode kinetics are outlined. These include discreteness-of-charge effects in the presence of specific adsorption, solvent effects in electron transfer reactions, and effects related to the distribution of charge in polyatomic reactants. The importance of studies at single crystal electrodes is emphasized, and the development of a single crystal ultramicroelectrode described. Finally, a method of improving the estimate of the diffuse layer potential drop on the basis of Monte Carlo simulations is presented.

Introduction

This paper describes the developments in the study of double layer effects in electrode kinetics during the last 50 years as I see them personally. The first mention of this subject appears in a paper by Frumkin in 1933 [1, 2]. Frumkin was very interested in the kinetics of electroreduction of the H⁺ ion. He observed that the current due to the reduction of hydrogen ions from solutions of a dilute acid at a mercury electrode is independent of the acid’s concentration at constant overpotential. This observation was attributed to a change in the concentration of the H⁺ ion at the reaction site in the double layer, together with a shift in the equilibrium potential for the reaction with change in acid concentration in the bulk. Another topic of interest for double layer effects in electrode kinetics was the electroreduction of anions. In 1949, Tatiana Kryukova [3] described the deep minimum that she observed in current–voltage curves for the reduction of peroxydisulfate anion (S₂O ²⁻₈ ) at a dropping mercury electrode in solutions of low ionic strength. In further work on this system and on the reduction of [Fe(CN)₆]^3-, Frumkin and Florianovich [4] attributed the minimum to a strong repulsion of the reactant from the reaction site in the double layer at potentials negative of the point of zero charge (pzc). Although the variation in current with electrolyte concentration could be explained, the dependence of the current on the nature of the cation of the electrolyte was not well understood [5].

Frumkin’s theory of double layer effects was based on the assumption that the reaction site in the double layer was at the outer Helmholtz plane (oHp) where the average potential is ϕ ^d. The expression for the potential dependence of the rate constant for a simple electron transfer reaction

$$ A + {e^{ - }} \to B $$

(1)

was written as

$$ \ln {k_{\rm{f}}} = \ln {k_{\rm{f0}}} - {z_{\rm{A}}}f{\phi^{\rm{d}}} + \alpha f\left( {{\phi^{\rm{d}}} - {\phi^{\rm{m}}}} \right) $$

(2)

Here, k _f is the forward rate constant; k_f0, the value when ϕ^m =0; ϕ^m, the electrode potential on the rational scale; α, the transfer coefficient; and $f = F/RT$. The term z _A fϕ ^d accounts for the fact that the local concentration of the reactant A with charge z _A on the oHp is different than in the bulk. The term in αf(ϕ ^d − ϕ ^m) accounts for the fact that the electron is transferred through the potential difference ϕ ^m − ϕ ^d, not through the potential difference ϕ ^m − ϕ ^s where ϕ ^s is the potential in the bulk of the solution (ϕ ^s = 0). Assuming that the charge on the reactant is known, the left hand side of Eq. 2 is corrected for the change in concentration of reactant A on the oHp, and one writes

$$ \ln {k_{\rm{f}}} + {z_{\rm{A}}}f{\phi^{\rm{d}}} = \alpha f\left( {{\phi^{\rm{d}}} - {\phi^{\rm{m}}}} \right) $$

(3)

This is known as a corrected Tafel plot (cTp) and can be constructed if the appropriate double layer data are available.

In 1965, Delahay’s monograph, “Double Layer and Electrode Kinetics” appeared [6]. This reviewed activity in the field up to the early 1960s. Other than the work of Frumkin, significant studies were carried out by Gierst [7] and by Delahay himself [6].

In the present paper, a review of activity in the field of double layer effects in electrode kinetics is presented. The developments in the field are discussed chronologically for each of the five decades beginning in 1960.

The 1960s

I first heard of the double layer in a series of lectures given by Professor Remy Barradas in 1962 to graduate students in the Chemistry Department at the University of Toronto. He introduced the main concepts and told us about the work of Alexander Frumkin in Moscow and in the laboratories of John Bockris in the US, Roger Parsons in Great Britain, and Brian Conway in Canada. I was enticed by the subject matter and decided to do my post-doctoral studies on double layer problems with Roger Parsons at the University of Bristol.

When I arrived in Bristol in January 1964, Parsons suggested that I try to study the electroreduction of anions in a non-aqueous solvent. At that time, we did not realize that polyvalent anions are impossible to dissolve in most non-aqueous solvents, especially aprotic solvents. In the end, I studied the electroreduction of periodate anion in aqueous solutions of high pH. This turned out to be a complex reaction, not really suitable to elucidating the details of the double layer role [8].

In 1966, I moved to the University of Guelph in Canada as an assistant professor. Guelph had formerly been the agricultural faculty of the University of Toronto, and the Chemistry Department did not have much of a research program. Nevertheless, I managed to attract a few students and begin a modest research program in non-aqueous electrochemistry. We decided to try to dissolve peroxydisulfate in formamide, a solvent with a very high relative permittivity (108) which I had not tried in Bristol. Of course, there was no problem dissolving polyvalent anions in this solvent, and we were able to study the electroreduction of anions in formamide. We observed that the current in the minimum at negative charge densities for the reduction of S₂O ²⁻₈ depended on the nature of the alkali metal cation in the order Li⁺ < Na⁺ < K⁺ < Cs⁺ [9]. A similar observation was made earlier for this system when it was studied in water [5]. The argument that the cation effect is due to ion pairing of the reactant with the alkali metal cation was more difficult to accept in formamide because of its high relative permittivity. Later, the work in formamide was extended to the ferricyanide system [10]. Considerable thought was given to developing a method of analyzing the experimental data to obtain an estimate of the charge on the reacting species moving through the double layer [11]. The results of our work on the electroreduction of anions were submitted to the international meeting on electrochemistry (CITCE, now ISE) which was held in Prague in October 1970 [12] (Fig. 1).

Fig. 1

Plots of the current i divided by the diffusion limited current i_d on the rational potential scale ϕ ^m for the electroreduction of peroxydisulfate anion at a Hg electrode in various 0.01 M base electrolyte solutions: 1 LiClO4, 2 NaClO4, 3 KClO4, 4 CsClO4 in formamide; 5 NaF, 6 KF, 7 CsF in water

Roger Parsons published an important paper on double layer effects in electrode kinetics in 1969 [13]. He analyzed the effect of specifically adsorbed halide ions on the kinetics of electroreduction of H⁺ ion at an Hg electrode and showed that the acceleration due to the adsorbed anions was greater than predicted by the simple Frumkin theory. He proposed that the potential dependence of the rate constant for a simple electron transfer process be written as

$$ \ln {k_{\rm{f}}} = \ln {k_{{{\rm{f}}0}}} - {z_{\rm{A}}}f{\phi^{\rm{d}}} + \alpha f\left( {{\phi^{\rm{d}}} - {\phi^{\rm{m}}}} \right) - \ln {\gamma_{ \ne }} $$

(4)

The additional term γ _≠ is the activity coefficient of the activated complex, which comes from transition state theory. Parsons argued that, in the absence of specific adsorption, γ _≠ does not change with electrode potential so that Eq. 2 gives an adequate description of the potential dependence of the rate constant. However, when specifically adsorbed ions which can interact attractively with the reactant are present, γ _≠ does vary significantly with potential. Parsons showed that the additional accelerating effect could be estimated from the parameters of the adsorption isotherm for the anions.

The 1970s

In September 1970, I traveled to the conference in Prague where I presented our work done in formamide. There I met Professor Frumkin who was very interested in this study. Frumkin presented a study of the electroreduction of S₂O ²⁻₈ at different metals, namely lead, cadmium, tin, and bismuth [14]. The current minimum appeared at different potentials due to a change in the pzc with metal nature. This work gave unambiguous proof that the origin of the effect is in the double layer. Frumkin told me that they had also attempted to study anion electroreduction in non-aqueous solvents but that solvents such as formamide were very difficult to obtain in Russia. I was very impressed with Frumkin’s deep understanding of double layer problems and decided to try and arrange a visit to his laboratory in Moscow.

In the summer of 1971, Sam Levine from the Mathematics Department of the University of Manchester visited my group in Guelph. This was the start of a long collaboration on double layer problems. Sam was a Canadian who settled in England after his university studies. He was active in theoretical work on double layer problems and visited Canada every summer. He taught me the importance of understanding ion adsorption at polarizable interfaces from an electrostatic point of view. This involved developing a detailed model for the potential at an adsorbed ion considering its images formed in the conducting electrode. As a result of our work that summer, we were able to recast the work of Parsons in a very general way which we described as the discreteness-of-charge effect in electrode kinetics [15].

In January 1972, I was invited to the Gordon Research Conference on Electrochemistry in Santa Barbara. These meetings attracted all the major names in American electrochemistry. I discovered that the double layer was not a popular topic for American electrochemists, but I did meet Robert de Levie from Georgetown University and David Mohilner from Colorado State University. Both of these men had groups involved with double layer research.

In September 1972, I traveled to Moscow for a 6-month exchange visit in Frumkin’s laboratory. On the way to Moscow, I stopped off in Warsaw to visit Zbigniew Galus. Galus was eager to send young scientists to my laboratory in Guelph. This visit led to an excellent collaboration. For the next 12 years, I always had someone from Poland in my laboratory. In Moscow, I started with a visit to Frumkin’s Electrochemistry Department at Moscow State University. After familiarizing myself with the experiments going on at the University, I joined the theoretical group at the Institute of Electrochemistry on Leninsky Prospect. There I worked with Valentin Krylov and Yury Kharkhats on problems related to the role of the double layer in electrode kinetics. On December 14, I gave a lecture in the institute entitled “Discreteness of Charge Effects in Electrode Kinetics” in Russian (Fig. 2). It was a difficult job but I managed, and Frumkin was quite pleased. I stayed in Moscow until the end of March 1973 and was able to write three papers with my Russian colleagues [16–18].

Fig. 2

Seminar announcement at the Institute of Electrochemistry, Moscow, USSR for 14 December 1972. The title is “Effects related to the discreteness of charge in electrochemical kinetics,” and the speaker is W. Fawcett (У Фoceтт)

I attended the Gordon Conference in Santa Barbara in January 1974 where I met Michael Weaver, a post-doctoral student in the laboratory of Fred Anson at Caltech. Weaver and Anson were interested in double layer effects on transition metal complexes. They established criteria for distinguishing between inner sphere and outer sphere electron transfer reactions [19]. They synthesized a series of complex cations of the general formula [Cr(H₂O)₅X]²⁺ or [Co(NH₃)₅X]²⁺ where X⁻ is a monovalent anion, and studied the effect of adsorbed I⁻ anion on the kinetics of the reduction reaction at an Hg electrode. When X⁻ was an adsorbing anion such as Br⁻ or CN⁻, the reactant was attached to the electrode through the anion, and the electron transfer was termed inner sphere. On the other hand, when X⁻ was a non-adsorbing anion such as F⁻, the reactant was not adsorbed and the electron transfer was termed outer sphere.

Fred Anson invited me to spend a sabbatical year in his laboratory at Caltech, and I arrived in Pasadena in the summer of 1976. Anson was especially interested in double layer effects in solutions of low ionic strength in which the electrode field reached large values. Sears and Anson [20] showed using chronocoulometry that the charge due to adsorbed anions at positive charge densities σ _a was approximately equal to the electrode charge density σ _m at positive charge densities. Perfect cancelation of σ _m by σ _a would result in the disappearance of the diffuse layer. However, perfect cancelation of the electrode charge over a wide potential range is impossible according to the second law of thermodynamics. Furthermore, it may be shown on the basis of an adsorption isotherm based on the electrochemical potential of the adsorbed anion in the double layer that σ _a is slightly less than σ _m so that large values of the potential drop across the diffuse layer are found [21]. This was confirmed experimentally by Anson and Parkinson [22] using Eu²⁺ and V²⁺ as kinetic probes in the same dilute solutions.

The first of a series of very talented Polish post-doctoral students, Andrzej Lasia joined my group in 1976. He set up experiments to study electrode kinetics using impedance methods and carried out a study of the effects of ion pairing on the electroreduction of nitromesitylene [23].

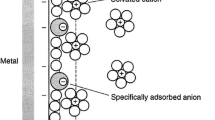
When I returned to Canada from Caltech in 1977, Andrzej Baranski from Warsaw joined my group. His first project was to study the kinetics of reduction of the alkali metal cations at Hg from non-aqueous media. He very quickly showed that the Gibbs activation energy for the process increased with the Gibbs energy of solvation of the cation in a given solvent [24]. He developed a mechanism for the amalgam formation process in which the rate determining step was ion transfer through the inner part of the double layer [25, 26]. This work was later extended to the alkaline earth metal ions [27]. In the ion transfer mechanism three locations for the cation are identified in the double layer (see Fig. 3). In position “c” the fully solvated cation is at its distance of closest approach; in position “b,” the cation has moved closer to the electrode replacing some of the solvent molecules solvating the electrode in an ion transfer step; in position “a,” the cation is adsorbed on the electrode surface in an adsorption step; finally, the metal ion is fully incorporated in the mercury phase in the incorporation step. The potential dependence of each of these steps was examined in detail somewhat later [28], and the large variation in the observed transfer coefficient explained. The ion transfer mechanism of Baranski and Fawcett differs significantly from the electron transfer mechanism proposed earlier by Losev [29] which involves formation of atoms and intermediate ions such as Mg⁺ in the double layer.

Fig. 3

Model for the passage of a Na⁺ ion through the compact region of the double layer. The solvent (dimethylformamide), predominant counter ion (tetraethylammonium cation), and reactant are represented by hard spheres with the following radii: DMF = 340 pm, TEA⁺ = 400 pm, and Na⁺ = 95 pm. Locations a, b, and c correspond to the passage of Na⁺ from a fully solvated ion at its distance of closest approach at c to an adsorbed species at a

The 1980s

In 1981, Sam Levine celebrated his 70th birthday, and a special issue of the Canadian Journal of Chemistry with contributions from scientists working on double layer problems was prepared in his honor. My paper dealt with the details of discreteness-of-charge effects in electron transfer kinetics as a function of position in the double layer [30]. Three types of double layer effects were described.

A type I effect occurs when an ion reacts in a double layer environment which contains mainly ions of the same sign. In this case, the activity coefficient of the activated complex is given by

$$ \ln {\gamma_{ \ne }} = \left( {{z_{\rm{A}}} - \alpha } \right)f\lambda \left( {{\phi^{\rm{m}}} - {\phi^{\rm{d}}}} \right) $$

(5)

where

$$ \lambda = {K_{\rm{md}}}/{K_{\rm{rd}}} $$

(6)

Here, K _md is the integral capacity of the region between the metal electrode and the reaction plane, and K _rd, that between the reaction plane and the oHp. Frumkin [2] had derived this relationship earlier in connection with his analysis of double layer effects on the electroreduction of H⁺ at Hg electrodes.

A type II effect occurs when an ion reacts in a double layer environment which contains mainly ions of the opposite sign. An example is the electroreduction of peroxydisulfate anion at negative charge densities on Hg with non-adsorbed cations on the oHp. The expression for the activity coefficient of the activated complex is then

$$ \ln {\gamma_{ \ne }} = \left( {{z_{\rm{A}}} - \alpha } \right)f\lambda \left( {{\phi^{\rm{m}}} - {\phi^{\rm{d}}}} \right) + \frac{{{a_{\pm }}{\sigma_{\rm{d}}}}}{{RT}} $$

(7)

The additional term in Eq. 7 describes the attractive interaction between the anionic reactant and the cations on the oHp whose local charge density is σ _d. The interaction coefficient is a _≠ which depends on the nature of the attracting ion.

The most complex double layer effect, type III, occurs when both cations and anions are present in the vicinity of the oHp in significant concentrations. One example of this situation occurs when anions are contact adsorbed on a polarizable electrode. The expression for ln γ _≠ is then quite complicated containing both electrostatic interaction terms and an entropic coverage term. If the logarithm of the forward rate constant in the presence of contact adsorption, ln k _fa, is compared to that in its absence, lnk_f, for constant (ϕ ^m − ϕ ^d), the following expression is obtained for the difference between these quantities

$$ \Delta = - \frac{{\left( {{z_{\rm{A}}} - \alpha } \right)f\left( {1 - \lambda } \right)\left( {1 - g} \right)}}{{{K_{\rm{rd}}}}}{\sigma_{\rm{a}}} - \frac{{{a_{ \ne }}{\sigma_{\rm{a}}}}}{{RT}} + {p_{ \ne }}\ln \left( {1 - {\sigma_{\rm{a}}}/{\sigma_{\rm{am}}}} \right) $$

(8)

Clearly, the change in ln k _f is a function of the charge density due to the contact adsorbed ions, σ _a. The dimensionless factor g is close to unity and is given by

$$ g = \frac{{{C_{\rm{d}}} + {K_{\rm{rd}}}}}{{{C_{\rm{d}}} + {K_{\rm{md}}}}} $$

(9)

where C _d is the differential capacity of the diffuse layer. Finally, p _≠ is the number of solvent molecules displaced by the activated complex on entering the inner layer.

Several studies of discreteness-of-charge-effects involving contact adsorbed anions were carried out including the effect of adsorbed iodide anions on the electroreduction of tetrathionate anion [31], the effect of adsorbed nitrate anions on the electroreduction of hexamminocobalt(III) cation [32], and the effect of adsorbed iodide anions on the electroreduction of monofluoropentaquochromium(III) cation [33]. The final study involved the elecroreduction of monofluoropentamminocobalt(III) cation in the presence of adsorbed nitrate anions [34]. The effects of adsorbed anions on the kinetics of this reactant were studied in detail in Weaver’s laboratory [35, 36]. They concluded that the reactant was an ideal choice for probing the double layer to obtain estimates of the potential drop across the diffuse layer, ϕ ^d. The analysis presented in [34] showed that such a conclusion cannot be supported when the detailed analysis of discreteness-of-charge effects is carried out.

In January 1984, I moved to the University of California in Davis. My main task was to establish a program in analytical chemistry at both the undergraduate and graduate levels. I soon found out that research funding was much more difficult to obtain in the US compared to Canada, but slowly I set up a research lab and attracted a few graduate students. One of these students, Colby Foss was very interested in solvent effects in electron and ion transfer reactions [37]. The seminal contribution to this subject was made by Kapturkiewicz and Behr [38] in Warsaw who studied the effect of solvent on the kinetics of electron transfer to three different salene complexes. They found a linear correlation between the logarithm of the rate constant for electron transfer, ln k _et, and the logarithm of the solvent viscosity, ln η, for eight aprotic organic solvents. The solvents ranged from acetonitrile (AcN) with a low viscosity to hexamethylphosphoramide (HMPA) with a very large viscosity. Noting that solvent viscosity can be related to the solvent relaxation time for rotational diffusion, they argued that the observed solvent effect is related to the effect of solvent relaxation on the formation of the activated complex for electron transfer. In fact, Calef and Wolynes [39, 40] showed this to be the case on the basis of theoretical arguments. In the fall of 1983, Barbara Behr visited Michael Weaver, now a professor at Purdue University, and presented a lecture describing their results for solvent effects on heterogeneous electron transfer. The Weaver group quickly became involved in this field and produced two papers in 1985 describing solvent effects on electron transfer reactions involving the metallocenes [41, 42]. In these papers, the authors correctly point out that the relevant quantity in the pre-exponential factor of the rate constant is the solvent’s longitudinal relaxation time τ _L. They collected the dielectric relaxation data from the literature and showed that τ _L varied from 0.2 ps in AcN to 8.9 ps in HMPA. However, for reactions such as the oxidation of ferrocene, electron transfer is too fast to be studied by the experimental methods available at that time.

The expression developed by the theoreticians for the standard rate constant corrected for double layer effects k _sc is

$$ {k_{\rm{sc}}} = \frac{{\kappa {K_{\rm{p}}}}}{{{\tau_{\rm{L}}}}}{\left( {\frac{{\Delta G_{\rm{os}}^{{*}}}}{{4\pi RT}}} \right)^{{1/2}}}\exp \left( {\frac{{ - \left( {\Delta G_{\rm{is}}^{{*}} + \Delta G_{\rm{os}}^{{*}}} \right)}}{{RT}}} \right) $$

(10)

Here, κ is the electronic transmission coefficient; K _p, the equilibrium constant for precursor complex formation; τ _L, the longitudinal relaxation time; $\Delta G_{\rm{is}}^{*}$, the inner sphere Gibbs activation energy; and $\Delta G_{\rm{os}}^{*}$, the corresponding outer sphere quantity. The outer sphere activation energy and the longitudinal relaxation time depend on the nature of the solvent. The Marcus expression for $\Delta G_{\rm{os}}^{*}$ is

$$ \Delta G_{\rm{os}}^{{*}} = \frac{{{N_{\rm{L}}}e_0^2}}{{32\pi {\varepsilon_0}RT}}\left( {\frac{1}{a} - \frac{1}{R}} \right)\left( {\frac{1}{{{\varepsilon_{\rm{op}}}}} - \frac{1}{{{\varepsilon_{\rm{s}}}}}} \right) $$

(11)

N _L is the Avogadro constant; e ₀, the fundamental electronic charge; ε ₀, the permittivity of free space; a, the radius of the reactant represented as a sphere; R, the distance to the reactant’s image in the conducting electrode; ε _op, the relative permittivity at optical frequencies; and ε _s, the relative static permittivity. The solvent-dependent terms come from the relative permittivites so that Eq. 11 may be simplified to

$$ \Delta G_{\rm{os}}^{{*}} = \gamma {\delta_{\rm{s}}} $$

(12)

where γ represents the solvent-independent terms and δ _s, the solvent-dependent Pekar factor, that is the last bracketed term in Eq. 11. For an adiabatic reaction (κ = 1), substituting Eq. 12 into Eq. 10 and taking the Pekar factor from the pre-exponential term to the left hand side, one may write

$$ \ln \left( {{k_{\rm{sc}}}/\delta {{_{\rm{s}}^{{{1/2}}}} }} \right) = \ln A - \frac{{\Delta G_{\rm{is}}^{{*}}}}{{RT}} - \ln {\tau_{\rm{L}}} - \frac{{\gamma {\delta_{\rm{s}}}}}{{RT}} $$

(13)

where A includes all the solvent independent terms from the pre-exponential factor. For fast reactions, a variation in δ _s with solvent nature is often negligible. It follows that a plot of ln k _sc against ln τ _L should be a straight line with a slope of −1. This is illustrated in Fig. 4 using data for the electro-oxidation of ferrocene obtained in nine aprotic solvents [43].

Fig. 4

Plot of the logarithm of the rate constant k _s in centimeters per second for the electro-oxidation of ferrocene at a Pt electrode in various solvents at 285 K against the logarithm of the solvent’s longitudinal relaxation time τ _L in ps. The solvents are acetonitrile (AcN), acetone (AC), butyronitrile (BuN), dichloroethane (DCE), dichloromethane (DCM), dimethylformamide (DMF), dimethylsulfoxide (DMSO), propylene carbonate (PC), and tetrahydofuran (THF). The straight line is drawn with unit slope

A particularly impressive study of the electro-oxidation of 1,2-diaminobenzene was carried by Marcin Opallo in Warsaw involving 12 different solvents, both protic and aprotic [44]. Opallo showed that the dependence of the Gibbs activation energy on solvent nature is much less than that on the pre-exponential factor, and obtained an excellent correlation between the logarithm of the electron transfer rate constant and the logarithm of the longitudinal relaxation time for data in the aprotic solvents. He also showed that the behavior of the protic solvents was clearly different.

Fawcett and Foss [37] showed that the solvent effect on the pre-exponential factor could be separated from that in the activation energy using regression analysis involving two independent variables, namely, the longitudinal relaxation time and the Pekar factor. For adiabatic reactions the data were analyzed using Eq. 13. A more general form of this equation valid for weakly adiabatic reactions [45] is

$$ \ln \left( {{k_{\rm{sc}}}/\delta_{\rm{s}}^{{{1/2}}}} \right) = \ln A - \frac{{\Delta G_{\rm{is}}^{{*}}}}{{RT}} - \theta \ln {\tau_{\rm{L}}} - \frac{{\gamma {\delta_{\rm{s}}}}}{{RT}} $$

(14)

Equation 14 is based on the theoretical work of Nadler and Marcus [46], the quantity θ being a fraction between zero and one. Fawcett and Foss [47] also investigated solvent effects in non-Debye solvents such as the alcohols. It was shown that the high frequency limiting value of τ _L [48] is the appropriate value when comparison is made with simple Debye solvents such as AcN, dimethylformamide, acetone, and dimethylsulfoxide.

The 1990s

The availability of ultramicroelectrodes (umes) in the 1980s led to an increase in studies of fast electron transfer reactions [49, 50]. These experiments often involved ultrafast cyclic voltammetric methods and were plagued with problems involving iR drop [51]. In 1991, Michael Weaver invited me to give a paper at a symposium he was organizing at the Spring Meeting of the Electrochemical Society in Washington, DC. I submitted a paper together with Andrzej Baranski on the kinetics of electro-oxidation of ferrocene in nine aprotic and three protic organic solvents [43]. Baranski had developed an ac admittance technique for studying fast electron transfer reactions at umes and had carefully assessed its limitations [52]. Weaver accepted our paper but told me that Nathan Lewis at Caltech had developed a technique for fabricating umes of nanometer dimensions (so-called nanodes) and measured a rate constant for the electro-oxidation of ferrocene in AcN which was 220 cm s⁻¹ [53]. This rate constant was 90 times higher than our result (3 cm s⁻¹), and certainly higher than any heterogeneous electron transfer rate constant known at that time. Baranski and I read the Lewis paper and tried to understand the very large disagreement. By the time we arrived in Washington for the conference, Baranski had offered an explanation for the Lewis result based on the difficulty in sealing glass to platinum [54]. Needless to say, the discussion at the conference was intense. In the end, the Lewis group was not able to reproduce their results which were attributed to the problems associated with fabricating umes of such small dimensions [51].

In 1992, Marcin Opallo working in Davis applied the Baranski technique to measure the kinetics of electroreduction of buckminsterfullerene in benzonitrile [55]. Since the reactant is a large sphere, it is an ideal system for testing Marcus’ theory. Analysis of the experimental data revealed that the Marcus estimates of $\Delta G_{\rm{os}}^{*}$ and $\Delta H_{\rm{os}}^{*}$ are slightly bigger than the experimental values. However, smaller values for these quantities which are closer to the experimental values are obtained when they are estimated using the mean spherical approximation (MSA) [56]. The expression for $\Delta G_{\rm{os}}^{*}$ in the MSA is

$$ \Delta G_{\rm{os}}^{{*}} = - \frac{{{N_{\rm{L}}}e_0^2}}{{32\pi {\varepsilon_0}}}\left[ {\frac{1}{a}\left( {1 - \frac{1}{{{\varepsilon_{\rm{op}}}}}} \right)} \right] - \frac{1}{{(a + {\omega_{\rm{s}}})}}\left( {1 - \frac{1}{{{\varepsilon_{\rm{s}}}}}} \right) $$

(15)

The polarization parameter ω _s corrects for the discrete nature of the solvent molecules in the vicinity of the reactant; it depends on the nature of the solvent and whether A is a cation or an anion. Imaging effects have been neglected in Eq. 15.

An interesting study of the effects of tetraalkylammonium cations (TEA⁺) on the kinetics of heterogeneous electron transfer was carried out by Opallo and Fedurco [57]. They studied the reduction of nitromesitylene at mercury in propylene carbonate solutions containing TEAClO₄ with the alkyl chains increasing in length from ethyl to octyl. As the alkyl chain increased in length, the standard rate constant decreased but the transfer coefficient and the enthalpy of activation were independent of the nature of the TEA⁺ cation. The experimental heat of activation is made up of three contributions, as follows:

$$ \Delta H_{\rm{ex}}^{{*}} = \Delta H_{\rm{is}}^{{*}} + \Delta H_{\rm{os}}^{{*}} + \theta \Delta {H_{\rm{L}}} $$

(16)

$\Delta H_{\rm{is}}^{{*}}$ is the inner sphere contribution to the activation enthalpy; $\Delta H_{\rm{os}}^{{*}}$, the outer sphere contribution; and ∆H _L, a contribution from the temperature dependence of the solvent’s longitudinal relaxation time. The fraction θ introduced in Eq. 16 depends on the degree of reaction adiabaticity and unity for a perfectly adiabatic reaction. Since $\Delta H_{\rm{ex}}^{{*}}$ is independent of the TEA⁺ cation, it was concluded that the reaction takes place surrounded mainly by solvent molecules. They estimated the activation enthalpy to be 28 kJ mol⁻¹, a result in agreement with the experimental value (28 ± 1 kJ mol⁻¹). Further analysis of these data showed that the logarithm of the rate constant at 25 C is linear in the radius of the TEA⁺ cation. Fedurco [58] studied medium effects on the electroreduction of benzophenone in seven aprotic solvents. Similar results were obtained as in previous work. In addition, he examined the effects of tetraalkylammonium cation size on the rate constant in AcN. The results were similar to those obtained earlier for nitromesitylene in PC.

In the 1990s, we began studies of double layer effects at single crystal gold electrodes. An early study involved the effects of surface reconstruction at Au(100) on the reduction of [Co(NH₃)₆]³⁺ and [Fe(H₂O)₆]³⁺ [59]. Another area of interest was double layer effects at self-assembled monolayers. In 1994, we described a model for the ionization of acidic head groups in self-assembled monolayers which took into consideration discreteness-of-charge effects [60]. The cutoff disc model described by Levine [61] was used to estimate these effects. In a later paper by Andreu and Fawcett [62], the hexagonal array method of Barlow and Macdonald [63] was used to treat the same problem. Discreteness-of-charge effects were also discussed for a self-assembled monolayer containing a simple redox couple [64]. In a later paper, the role of ion pairing on double layer effects in these systems was detailed [65].

In 1996, a study of solvent effects on the electroreduction of p-dicyanobenzene and the electro-oxidation of nickelocene were reported [66]. Both reactions were shown to be adiabatic with fast electron transfer rate constants. Kinetic data obtained at mercury were corrected for the double layer effect. The solvent effect on the rate constant and enthalpy of activation were consistent with the theory discussed earlier. In a subsequent paper, the role of the solvent and metal electrode in simple electron transfer reactions was discussed [67]. The role of the change in the pzc with the crystallographic orientation of single crystal electrodes was illustrated for the case of the [Fe(H₂O)₆]^3+/2+ redox couple. Another interesting study of solvent effects involved tetrakis(dimethylamino)-p-benzoquinone which may be both oxidized and reduced [68]. This work showed that the rate constants for the two processes were approximately equal in a given solvent but that the heat of activation for the reduction process was greater than that for the oxidation process. This is exactly what one would predict when the MSA is used to estimate the activation parameters rather than the simple Marcus theory [69].

In 1999, I attended the second Baltic conference on electrochemistry in Palanga, Lithuania where I presented our work on electron transfer through self-assembled monolayers using impedance spectroscopy [70, 71]. At this conference, I met Galina Tsirlina who told me about the importance of considering charge distribution effects in polyatomic reactants in the double layer. This had an important influence on the way we analyzed double layer effects in heterogeneous electron transfer reactions.

The last 10 years

In the late 1990s Magdalena Hromadova from the de Levie lab came to Davis as a post-doctoral student to work on double layer effects at Au single crystal electrodes. These experiments were done with highly purified perchloric acid as electrolyte in carefully purified water. Her first paper [72] described the electroduction of [Co(NH₃)₆]³⁺ at four different single crystals, namely, Au(100), Au(110), Au(111), and Au(210). Because the pzc varies from −0.1 V for Au(210) to +0.08 V for Au(111), one is able to study the kinetics of reduction of this cation over a very wide potential range (0.3 V). Analysis of the kinetic data showed that the effective charge on the reactant is 2.0. The apparent transfer coefficient from the corrected Tafel plots was 1.1, an unusually high result. The low reactant charge and high transfer coefficient were attributed to charge distribution effects in the reactant. In this case, Eq. 2 must be written as follows:

$$ \ln {k_{\rm{f}}} = \ln {k_{{{\rm{f}}0}}} - {w_{\rm{A}}} - \alpha f\left( {{\phi^{\rm{m}}} - {w_{\rm{A}}} + {w_{\rm{B}}}} \right) $$

(17)

w _A is the work done to bring the reactant through the double layer, and w _B, that for the product and ion specific adsorption is assumed to be absent. A cTp constructed using the effective charge on the reactant and the oHp potential is therefore

$$ \ln {k_{\rm{f}}} + {z_{\rm{Ae}}}{\phi^{\rm{d}}} = \ln {k_{{{\rm{f}}0}}} + \left( {{z_{\rm{Ae}}} - \alpha } \right)f{\phi^{\rm{d}}} - \left\langle w \right\rangle /RT - \alpha f\left( {{\phi^{\rm{m}}} - {\phi^{\rm{d}}}} \right) $$

(18)

where the average work for the reactant and product is defined as

$$ \left\langle w \right\rangle = (1 - \alpha ){w_{\rm{A}}} + \alpha {w_{\rm{B}}} $$

(19)

The slope of the cTp gives the apparent transfer coefficient α _a. On the basis of Eq. 18 α _a is given by

$$ {\alpha_{\rm{a}}} = \frac{{RT}}{F}\frac{{{\text{d}}\left( {\ln {k_{\rm{f}}} + {z_{\rm{Ae}}}{\phi^{\rm{d}}}} \right)}}{{{\hbox{d}}\left( {{\phi^{\rm{d}}} - {\phi^{\rm{m}}}} \right)}} = \alpha + \left( {{z_{\rm{Ae}}} - \alpha } \right)\frac{{{\text{d}}{\phi^{\rm{d}}}}}{{{\hbox{d}}\left( {{\phi^{\rm{d}}} - {\phi^{\rm{m}}}} \right)}} - \frac{{RT}}{F}\frac{{{\text{d}}\left\langle w \right\rangle }}{{{\hbox{d}}\left( {{\phi^{\rm{d}}} - {\phi^{\rm{m}}}} \right)}} $$

(20)

The true transfer coefficient α for a simple electron transfer process is 0.5. In the second term, the derivative is negative so that this term is negative and would lead to values of α _a less than 0.5. It follows that the contribution of the last term is large and positive. In other words, the average work involved in transporting the reactant and product through the double layer increases as the electrode potential moves in the negative direction. This is confirmed by the double layer data for the Au/solution interface.

Subsequent quantum chemical calculations [73] showed that the charge on the Co atom is 1.67 with a charge of 0.22 on each amino ligand. Furthermore, on the basis of geometrical considerations, the Co center of the complex is located outside the oHp [72, 73]. Our paper with Renat Nazmutdinov and Galina Tsirlina [73] had been submitted to a special issue of the Journal of Electroanalytical Chemistry honoring Fred Anson which was organized by Michael Weaver. Later in 2001, I contacted Mike by email to discuss charge distribution effects which are so important for the transition metal complexes which Anson and Weaver had studied earlier [19]. At the time, Mike was very busy writing proposals, but he promised to contact me by telephone. Unfortunately, that telephone conversation never took place. Sadly, Mike died unexpectedly early in 2002 close to his 55th birthday.

A study similar to that for [Co(NH₃)₆]³⁺ was carried out for the reduction of [Fe(H₂O)₆]³⁺ in perchloric acid at single crystal Au electrodes [74]. The effective charge on the reactant is +2, and the apparent transfer coefficient from corrected Tafel plots, 0.3. On the basis of the quantum chemical calculations the charge on the Fe atom is 2.52, and that on each of the aquo ligands, 0.09. The charge distribution and location of the reactant in the double layer allowed us to rationalize the experimental data. The most interesting study carried out by Hromadova was the reduction of [Co(NH₃)₅F]²⁺ at single crystal gold electrodes [75]. The effective charge on the reactant is 1.6 and the apparent transfer coefficient, 0.72. This ionic reactant has a dipole moment so that it is oriented with the electronegative F atom furthest from the electrode when it carries a negative charge. As with the previous systems, the results were consistent with the charge distribution in the polyatomic reactant. This is the first example of a reaction in which the effective charge on the reactant is non-integral.

One day in 2000, during a conversation with Magdalena, I made the comment that it was a pity that we could not fabricate an ultramicroelectrode that was also a single crystal so that double layer effects could be studied for very fast electron transfer reactions. My comment was overheard by a new graduate student from Slovakia, Vlado Komanicky. A month later, Vlado informed me that he had made single crystals of micron dimensions, and that he felt that he could incorporate these crystals in an ume. With incredible skill in working with such small crystals, Vlado succeeded, and a few months later we sent a paper describing the fabrication of Au single crystal umes to Angewandte Chemie [76]. We called these electrodes scumes. The huge success determined the direction of Vlado’s doctoral thesis. He showed that two crystallographic orientations could be harvested from the electrodeposition technique used to produce the crystals, namely, Au(111) and Au(100). The crystals were grown in a silicate gel which contained HCl and HAuCl₄. When a small current is passed through the gel between two gold electrodes, gold is deposited at the cathode and chlorine gas is formed at the anode. After 24 h, gold crystals appear in the gel in the vicinity of the anode. The conditions for nucleation and growth of these crystals are determined by the gel and its pH. First, the Au reacts with the Cl₂ to form a metastable Au(I) complex as follows:

$$ {\hbox{2 Au}} + {\hbox{C}}{{\hbox{l}}_{{2}}} + {2}\,{\hbox{C}}{{\hbox{l}}^{ - }} \to { 2}{\left[ {{\hbox{AuC}}{{\hbox{l}}_{{2}}}} \right]^{ - }} $$

(21)

The complex ion eventually disproportionates after diffusing from the vicinity of the electrode:

$$ {3}\,{\left[ {{\hbox{AuC}}{{\hbox{l}}_{{2}}}} \right]^{ - }} \to {\left[ {{\hbox{AuC}}{{\hbox{l}}_{{4}}}} \right]^{ - }} + {2}\,{\hbox{Au}} + {2}\,{\hbox{C}}{{\hbox{l}}^{ - }} $$

(22)

Komanicky also developed a method for producing Pt umes [77]. A Pt bead was formed at the end of a thin Pt wire in a methane flame. When the bead is annealed in the flame Pt(111) and Pt(100) facets are formed. A procedure was developed to encase one of these facets in soft sodium glass. Cyclic voltammetry in 0.5 M sulfuric acid yielded the typical current–voltage curve seen at Pt single crystals of macro dimensions [77]. Komanicky also studied the properties of a Au(100) scume and compared them with those of a single crystal of macro dimensions [78]. The work with Au and Pt scumes was summarized in a later paper [79].

Martin Muzikař came to Davis from the Czech Republic in 2002 and learned how to make the Au scumes from Vlado Komanicky. He then began to use these electrodes to study the electroreduction of [Ru(NH₃)₆]³⁺, a very fast reversible electron transfer reaction. First, he characterized the reaction at a polycrystalline Au electrode in aqueous perchloric acid using cyclic voltammetry, thereby obtaining the standard potential and the diffusion coefficient [80]. The admittance data were analyzed by two methods. In the standard Randles analysis, the admittance data at the standard potential are corrected for the solution resistance and double layer capacity in the absence of the reaction. Then by obtaining the admittance data as a function of frequency at the standard potential one is able to separate out the Warburg impedance and calculate the standard rate constant. The Baranski analysis is used to analyze admittance data as a function of potential at one frequency [52, 80]. The optimum frequency for carrying out the experiment is determined by the solution resistance [52]. Then experiments were carried out at Au(111) and Au(100) scumes. The rate constant for a given HClO₄ concentration was higher at Au(111) than at Au(100) [81]. Furthermore, it increased with increase in HClO₄ concentration, the highest value of k _s being 0.55 cm⁻¹ at Au(111) in 0.05 M HClO₄. The standard potential for the reaction is negative of the pzc at both electrodes, but it occurs at more negative potentials at Au(111). Thus, the accelerating effect of the double layer is greater at Au(111). The double layer data were used to estimate the apparent transfer coefficient at these single crystals, the values of α _a being 0.69 at Au(111) and 1.26 at Au(100). The large difference in these results is due to the fact that the oHp potential ϕ ^d changes much more with potential at the latter electrode. This study represents the first time that double layer effects were studied for a very fast electron transfer reaction. Unfortunately, the Au scumes could not be used in non-aqueous solvents because the cement used to fix the Au crystal in the scume was not stable in these solvents.

Maria Rusanova, a post-doctoral student from Moscow carried out a study of charge distribution effects for slower reactions involving transition metal cations using cyclic voltammetry at a hanging mercury drop electrode [82]. Quantum chemical calculations determined the fraction of the charge on the central metal ion and on each of the ligands. In the case of [Cr(H₂O)₆]³⁺, the Cr atom has a charge of 2.12 with a charge of 0.15 on each of the aquo ligands. For the product [Cr(H₂O)₆]²⁺, the charge on the central Cr atom is 1.79 with a charge of 0.035 on each aquo ligand. An analysis of the kinetic data shows that the effective charge on the [Cr(H₂O)₆]³⁺ reactant is 2.2. Furthermore, estimates of the effective charge on the product [Cr(H₂O)₆]²⁺ are greater than 1.2 so that the difference z _Ae − z _Be is less than one. Thus, a better expression for the cTp is

$$ \ln {k_{\rm{f}}} + {z_{\rm{Ae}}}f{\phi^{\rm{d}}} = \ln {k_{{{\rm{f}}0}}} - \alpha f\left( {{\phi^{\rm{m}}} - \delta {z_{\rm{e}}}{\phi^{\rm{d}}}} \right) $$

(23)

where $\delta {z_{\rm{e}}} = {z_{\rm{Ae}}}--{z_{\rm{Be}}}$. For this system, δz _e is equal to 0.68 in a solution of 0.3 M NaClO₄ + 0.001 M HClO₄.

For the [Eu(H₂O)₆]³⁺ reactant, the charge on the central Eu atom is only 1.36 with a charge of 0.27 on each of the aquo ligands. Quantum chemical calculations were not carried out for the product ion. Analysis of the kinetic data shows that the effective charge on the reactant is 1.7. This result is what one would expect on the basis of the quantum calculations. Our work on charge distribution effects was summarized in a review paper published in 2008 [83].

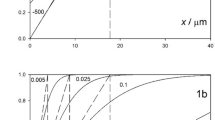
The analysis of double layer effects relies on the Gouy–Chapman (GC) theory to estimate the diffuse layer potential drop ϕ ^d. An important problem with GC theory is the fact that it ignores the finite size of the ions in the electrolyte. This may be demonstrated using Monte Carlo (MC) simulations. Beginning with the work of Torrie and Valleau in the early 1980s [84, 85], it was shown that the GC estimates of ϕ ^d are seriously in error especially when polyvalent ions predominate in the diffuse layer [86–88]. MC data for a 1:1 electrolyte at various concentrations for an ion size of 300 pm are shown in Fig. 5. The MC estimate of ϕ ^d is always less than the GC value, the difference increasing with increase in electrolyte concentration and electrode charge density. Corresponding results for a 2:1 electrolyte are shown in Fig. 6. At negative charge densities where the divalent cation is attracted into the diffuse layer, the departure from the GC value of ϕ ^d is quite large. It is clear that the GC theory cannot be applied to analyze double layer effects under these conditions.

Fig. 5

Plots of the potential drop across the diffuse layer ϕ ^d from the MC simulations for an ion diameter of 300 pm against the value calculated by GC theory ϕ ^d(GC) for varying concentrations of a 1:1 electrolyte: (black circle) 0.1 M, (black up-pointing triangle) 0.2 M, (black down-pointing triangle) 0.5 M, (black diamond) 1.0 M, and (black square) 2 M. Successive plots have been shifted vertically by 0.1 V for the sake of clarity. The straight lines drawn with unit slope show the GC predictions

Fig. 6

As in Fig. 5 but for a 2:1 electrolyte

In the GC theory, the potential ϕ ^d for a 1:1 electrolyte can be estimated from the equation

$$ \cosh \left( {\frac{{F\phi_{\rm{GC}}^{\rm{d}}}}{{RT}}} \right) = 1 + \frac{{{E^2}}}{2} $$

(24)

where E is the dimensionless electrode charge density given by σ _m = A _GC. A _GC is the Gouy–Chapman constant given by A _GC = (2RTε ₀ ε _s c _e)^1/2, and c _e, the concentration of a 1:1 electrolyte. In the hypernetted chain approximation of the integral equation approach, ϕ ^d is given by

$$ {\Xi_0}\cosh \left( {\frac{{F{\phi^{\rm{d}}}}}{{RT}} + {{\rm H}_0}} \right) = {a_0} + \frac{{{E^2}}}{2} $$

(25)

The function Ξ ₀ accounts for the hard sphere part of the effects of finite ion size on the value of ϕ ^d; in the limit of zero E, it is equal to the compressibility factor a₀. The function Η ₀ accounts for the electrostatic part of the effects ion size on the ionic atmosphere. These functions may be estimated from the MC simulations [88].

The MSA can only be applied to the diffuse layer problem in the limit of very small values of E. However, there are two important parameters used in the MSA which characterize the effects of ion size. One is the fraction of the volume occupied by the ions which is given by

$$ \varsigma = \frac{{\pi {N_{\rm{L}}}{c_{\rm{e}}}{\sigma^3}}}{3} $$

(26)

where σ is the ionic diameter and both ions have the same size (restricted electrolyte). The second parameter is the reciprocal of the thickness of the ionic atmosphere which is given in dimensionless units by

$$ 2\Gamma = {\left( {1 + 2\kappa \sigma } \right)^{{1/2}}} - 1 $$

(27)

where κ is the reciprocal of the ionic atmosphere thickness in Debye–Huckel theory. Because of finite ion, size 2Γ is always less than κσ. Smagala and Fawcett have shown that both Ξ ₀ and Η ₀ can be expressed as simple analytical functions of η and 2Γ on the basis of data from the MC simulations [89, 90]. For 1:1 electrolytes, the function Ξ ₀ is given by

$$ {\Xi_0} = {a_0}{\hbox{sech}}\left( {{a_1}E} \right) $$

(28)

$$ {\hbox{where}}\quad {a_0} = \frac{{1 + \varsigma + {\varsigma^2} - {\varsigma^3}}}{{{{(1 - \varsigma )}^3}}} - \frac{{{\Gamma^3}}}{{18\eta }} $$

(29)

$$ {\hbox{and}}\quad {a_1} = \frac{{5{\varsigma^{{1/2}}}}}{4} $$

(30)

The function Η ₀ is given by

$$ {{\rm H}_0} = {b_1}E + {b_3}{E^3} $$

(31)

$$ {\hbox{with}}\quad {b_1} = \Gamma /2 $$

(32)

$$ {\hbox{and}}\quad {b_3} = \frac{{{\Gamma^{{1.75}}}}}{7} - \frac{{4{\varsigma^{{1/2}}}}}{{25}} $$

(33)

Using these equations and similar equations for more complex electrolytes, improved estimates of ϕ ^d can be used in the analysis of double layer effects.

Concluding remarks

It is clear that the study of electron transfer kinetics has made tremendous progress during the last 50 years. Experimentally, the use of single crystal electrodes and umes has assisted this progress in an important way. However, the theoretical understanding of double layer effects has also improved. The importance of treating the double layer as a three-dimensional problem rather than as a simple one-dimensional problem is clear from the study of discreteness-of-charge effects. In addition, the reactant and product of the electron transfer cannot be modeled as a simple sphere with an embedded central charge. In general, the distribution of charge within these species must be considered within the potential distribution in the double layer. Solvent effects in both the pre-exponential factor and in the exponent of the rate constant for electron transfer are now well understood. Finally, on the basis of MC simulations improved estimates of ϕ ^d are available for analyzing double layer effects.