Halogen bonding and the σ-hole

According to the recent IUPAC definition: “A halogen bond occurs when there is evidence of a net attractive interaction between an electrophilic region associated with a halogen atom in a molecular entity and a nucleophilic region in another, or the same, molecular entity” [1]. Halogen bonding is a classical interaction in chemistry that has received considerable interest during the last decades due to a large increase of applications within wide areas of chemistry, medicine, and material science [2]. Although the denotation halogen bonding is relatively recent, the first literature reports of halogen bond complexes can be traced to the nineteenth century [3]. Mulliken was a pioneer in the theoretical analysis of halogen bond complexes and interpreted these as donor–acceptor complexes based on spectral analysis [4]. An interpretation that remained the commonly accepted paradigm until the beginning of the twenty-first century. However, already in 1992, Brinck, Murray, and Politzer showed that the halogen bond donating capability of halogenated methanes can be explained by a region of positive surface electrostatic potential at the end (tip) of the halogen atom along the R–X axis [5].

In 2005 Clark, Murray, and Politzer, together with Hennemann, introduced the σ-hole concept to rationalize the positive surface electrostatic potential of the halogen; the σ-hole was originally viewed as an electron depletion at the halogen tip formed owing to the singly occupied valence p-orbital of the halogen in the direction of the R–X bond [6]. Clark, Murray, and Politzer have remained the main advocates of the σ-hole concept, continuously revising and developing the theoretical interpretation of the σ-hole and its importance for halogen bonding [7,8,9,10,11,12]. Whereas the σ-hole bonding originally was considered mainly electrostatic in nature, Clark, Murray, and Politzer have in recent years emphasized the importance of polarization as a natural and inseparable companion to the electrostatic interaction [9,10,11]. Furthermore, dispersion is considered as polarization, following Feynman’s interpretation [13] based on the Hellmann-Feynman theorem [10]. Charge transfer, on the other hand, is argued to lack physical significance for noncovalent interactions and to be the result of mathematical modeling, as there is no rigorous approach to separate intra-molecular and inter-molecular reorganization of the electron density [10].

Although the σ-hole interpretation has received considerable acceptance within the scientific community, it has also continuously been challenged by scientist arguing that charge-transfer and orbital interactions must be considered for a complete description of halogen bonding [14,15,16,17,18]. In a recent study, Head-Gordon and coworkers analyzed the potential energy surfaces for a series of complexes of the type CX3I•••Y− (X=F, Cl, Br and Y=F, Cl, Br, I) by absolutely localized molecular orbitals energy decomposition analysis (ALMO-EDA) [18]. The ALMO-EDA is designed to provide a lower bound to the charge-transfer energy. In this analysis, it was found that for any given Y− the complexation energy of CX3I•••Y− decreases in the order F, Cl, Br, I, whereas the sum of the Pauli repulsion, electrostatic, and polarization energies increases in the same order. The decrease in the complexation energy was consequently attributed to the charge transfer energy, which in ALMO-EDA is defined as the remaining part of the interaction energy when other energy contributions have been subtracted out.

In a recent article, Clark and Heßelmann responded to the work of Head-Gordon and coworkers by showing that the interaction energy of the entire set of complexes is linearly correlated to the surface electrostatic potential of the σ-hole, if the surface electrostatic potential is computed from the electron density of the halogen bond donor polarized by a unitary negative charge at the position of the negative halide ion [12]. The correlation coefficient is excellent, R2 = 0.994, demonstrating that the variation in complexation energy is fully reproduced by the polarized surface potential.

The objective of the current work has been to investigate the point charge (PC) approximation in more detail. The use of a PC-model is intriguing in its simplicity and it allows for the exclusion of charge-transfer effects, as there are no electrons that can be transferred. However, it remains to be determined whether such a model can provide consistent results upon larger variations in the chemical environment of the halogen atom, rather than just changing the halogen substituent in CX3I. In addition, we evaluated the PC approximation within the classical theory of electrostatics and polarization, as this theory shows that the interaction energy depends upon the cost of polarizing the electron density and therefore cannot be expressed by the electrostatic potential of the polarized charge distribution alone. A further advantage is that the classical theory allows for the interaction energy to be rigorously separated into contributions from electrostatics and polarization.

In this work, we studied a range of halogen bonded complexes of the types; R–Br•••Br− where R is a substituted methyl group, i.e., R = CH3, CH2NH2, CH2F, CH2Br, CH2CHO, CH2CN, CH2NO2, CF2CN, CF2NO2, CF3, and CBr3; and R´–C≡C–Br•••Br− where R is a substituent, i.e., R´=H, NH2, F, Br, CN, NO2, and the aromatic substituents R´=C6H5, C6F5, and p-C6H4NO2. The selection of R–Br•••Br− complexes was inspired by the work of Rosokha et al. [15], as they argue that the halogen bond in these types of complexes has a significant contribution from charge transfer due to the interaction of the Br lone pair with the C–Br σ*-orbital. Complexes of the R–Br•••Br− type are expected to behave similarly to R–I•••Br− complexes, which were studied by Head-Gordon and coworkers, but the former type of complexes is easier to characterize theoretically; Br, in contrast to I, can be modeled without consideration of relativistic effects. We chose to include a group of alkyne halogen bond donors as previous studies have indicated that these generally form stronger complexes than alkyl halogen bond donors, and they exhibit larger substituent effects [19, 20]. Furthermore, the chosen substituents include both inductive and resonance acceptors, as we hypothesized that the latter type would promote charge transfer more effectively. Despite the efforts to maximize the potential for charge transfer, our results show that the halogen bond interactions of these complexes are governed by electrostatics and polarization and that charge transfer is of negligible importance.

Methods and procedure

The halogen bonded complexes have been analyzed by full structure optimization using Kohn–Sham density functional theory at the M06-2X/6–311+G(d,p) level. The M06-2X functional is highly accurate for main-group chemistry, including noncovalent interactions and it explicitly accounts for dispersion interactions [21]. It has been evaluated against the halogen bond benchmark data base (XB51) and been shown to provide excellent geometries and energies [22]. The RMSD of M06-2X for interaction energies is 0.43 kcal mol–1, which is much lower than, e.g., MP2 extrapolated to infinite basis set (RMSD = 0.92 kcal mol–1). The 6–311+G(d,p) basis set used herein is sufficiently flexible and diffuse to reduce the basis set superposition error to acceptable levels. Additional computations have been performed at the same level of theory using a point charge to represent the Br− anion. These computations used the optimized geometries of the halogen bonded complexes, but a negative point charge (−1 au) was placed at the position of Br−. In addition, the electrostatic potential was computed from the unperturbed density, and from the point charge perturbed density, of the halogen bond donors in the geometries of the complexes. All computations were performed using the Gaussian 16 suite of software [23].

The classical interaction energy of a point charge (PC)

The electrostatic potential of an atom or a molecule is rigorously defined by

$$ V\left(\mathbf{r}\right)=\sum \limits_A\frac{Z_A}{\mid {\mathbf{R}}_A-\mathbf{r}\mid }-\int \frac{\rho \left({\mathbf{r}}^{\prime}\right)d\mathbf{r}}{\mid {\mathbf{r}}^{\prime }-\mathbf{r}\mid } $$
(1)

where ZA is the charge on nucleus A located at RA, and ρ(r) is the electron density function. V(r) is a real physical observable and can be determined from an experimentally obtained charge distribution obtained by, e.g., diffraction methods. More commonly, V(r) is determined computationally by wavefunction theory or Kohn–Sham density functional theory. In this respect, it should be noted that V(r) is a one-electron property and as such less sensitive to computational level and basis set than, e.g., the electronic energy. The electrostatic interaction energy with a point charge is defined by

$$ \varDelta {E}_{\mathrm{ES}}^{\mathrm{PC}}= qV\left({\mathbf{r}}_q\right) $$
(2)

and corresponds to the energy of the Coulombic interaction between a point charge q located at rq and the static (unperturbed) charge distribution of the molecule. It equals the exact interaction energy in the limit of an infinitesimal point charge, as the polarization at this limit is negligible. It is also possible to compute V(r) from a polarized electron density. If VPC(r) refers to the potential obtained from a density polarized by a point charge q located at rq then qVPC(rq) is the energy of the Coulombic interaction between q and the polarized charge distribution of the molecule or atom. It must be noted, however, that this is not the same as the total interaction energy, as there is a cost of polarizing, or deforming, the electron density. According to the classical description of polarization, which is based on a linear response to the electric field generated by the point charge, the total interaction energy is given by

$$ \varDelta {E}^{\mathrm{PC}-\mathrm{Lin}}=1/2q\left[V\left({\mathbf{r}}_q\right)+{V}^{\mathrm{PC}}\left({\mathbf{r}}_q\right)\right] $$
(3)

The polarization energy, i.e., the classical induction energy, is defined by

$$ \varDelta {E}_{\mathrm{Pol}}^{\mathrm{PC}-\mathrm{Lin}}=\varDelta {E}^{\mathrm{PC}-\mathrm{Lin}}-\varDelta {E}_{ES}^{\mathrm{PC}}=1/2q\left[{V}^{\mathrm{PC}}\left({\mathbf{r}}_q\right)-V\left({\mathbf{r}}_q\right)\right] $$
(4)

and the cost of polarizing the electron density is the difference between the total interaction energy and the Coulombic interaction energy of the polarized system

$$ \varDelta {E}_{\rho -\mathrm{def}}^{\mathrm{PC}-\mathrm{Lin}}=\varDelta {E}^{\mathrm{PC}-\mathrm{Lin}}-q{V}^{\mathrm{PC}}\left({\mathbf{r}}_q\right)=-1/2q\left[{V}^{\mathrm{PC}}\left({\mathbf{r}}_q\right)-V\left({\mathbf{r}}_q\right)\right]=-\varDelta {E}_{\mathrm{Pol}}^{\mathrm{PC}-\mathrm{Lin}} $$
(5)

The quantum chemical PC-model of the halogen bond complexes

figure a

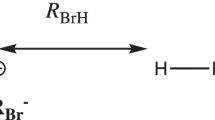
The scheme above shows the point charge model for the interaction of Br− with a halogen bond donor of the type R–Br. The nuclear geometry of R–Br is taken from the full geometry optimization of the complex, and the point charge (qBr− = − 1) is placed at the position (RBr−) of the Br nucleus in the complex. The total interaction energy (ΔEPC) between the point charge and R–Br is obtained as the difference in the Born–Oppenheimer energy with and without the point charge included in the electronic Hamiltonian. It should be noted that the relaxed geometry of R–Br in the complex is used for both calculations. The ΔEPC can be divided into an electrostatic interaction energy and a polarization (induction) energy

$$ \varDelta {E}^{\mathrm{PC}}=\varDelta {E}_{\mathrm{ES}}^{\mathrm{PC}}+\varDelta {E}_{\mathrm{Pol}}^{\mathrm{PC}} $$
(6)

where the electrostatic contribution can be computed directly from the electrostatic potential at RBr–,

$$ \varDelta {E}_{\mathrm{ES}}^{\mathrm{PC}}={q}_{{\mathrm{Br}}^{-}}V\left({\mathbf{r}}_q\right)=-V\left({\mathbf{R}}_{{\mathrm{Br}}^{-}}\right) $$
(7)

and the polarization energy is given by

$$ \varDelta {E}_{\mathrm{Pol}}^{\mathrm{PC}}=\varDelta {E}^{\mathrm{PC}}-\varDelta {E}_{\mathrm{ES}}^{\mathrm{PC}}=\varDelta {E}^{\mathrm{PC}}+V\left({\mathbf{R}}_{{\mathrm{Br}}^{-}}\right) $$
(8)

The energy cost of polarizing the electron density is analogous to Eq. 5 described by

$$ \varDelta {E}_{\rho -\mathrm{def}}^{\mathrm{PC}}=\varDelta {E}^{\mathrm{PC}}+{V}^{\mathrm{PC}}\left({\mathbf{R}}_{{\mathrm{Br}}^{-}}\right) $$
(9)

Furthermore, the polarization is expected to approximatively follow linear response, and thus

$$ \varDelta {E}^{\mathrm{PC}}\approx -1/2\left[V\left({\mathbf{R}}_{{\mathrm{Br}}^{-}}\right)+{V}^{\mathrm{PC}}\left({\mathbf{R}}_{{\mathrm{Br}}^{-}}\right)\right] $$
(10)

and

$$ \varDelta {E}_{\rho -\mathrm{def}}^{\mathrm{PC}}\approx -\varDelta {E}_{\mathrm{Pol}}^{\mathrm{PC}} $$
(11)

In fact, how well these relationships are fulfilled provides an indication to what extent the system behaves according to classical polarization theory.

Finally, there is an energy cost of deforming the nuclear geometry of RBr into its geometry in the complex. This term, ΔENuc−def, is simply computed as the difference in the quantum chemical energy (Born–Oppenheimer energy) of RBr at the two geometries. It should be remembered that the driving force for the deformation is to lower the total interaction energy of the complex.

PC approximation and the PES of CF3Br•••Br− and CBr4---Br−

We will first analyze the PC approximation with respect to the potential energy surfaces (PES) of the CF3Br•••Br− and CBr4---Br− complexes along the Br–Br− distance (R) as shown in Fig. 1. The relevant energy components at the equilibrium geometry of the complexes are presented in Table 1. Starting with CF3Br•••Br− we note that the PC interaction energy (ΔEPC) is very similar to the full quantum chemical interaction energy (∆EInt) at long R, i.e., distances beyond 5 Å. It can be further be noted that at distances longer than twice the equilibrium distance (R > 2 Req) the electrostatic interaction energy (\( \varDelta {E}_{\mathrm{ES}}^{\mathrm{PC}} \)) is only marginally higher than ΔEPC, e.g., 0.37 kcal mol–1 at R = 6.5 Å. However, the difference between ΔEPC and \( \varDelta {E}_{\mathrm{ES}}^{\mathrm{PC}} \), i.e., the polarization/induction energy (\( \varDelta {E}_{\mathrm{Pol}}^{\mathrm{PC}} \)), increases in magnitude as R decreases. At the equilibrium geometry of the complex (Req = 3.13 Å), \( \varDelta {E}_{\mathrm{ES}}^{\mathrm{PC}} \)= − 9.61 kcal mol–1 and \( \varDelta {E}_{\mathrm{Pol}}^{\mathrm{PC}} \)= −5.43 kcal mol–1, and thus \( \varDelta {E}_{\mathrm{Pol}}^{\mathrm{PC}} \) constitutes 36% of ΔEPC.

Fig. 1
figure 1

The full quantum chemical interaction energy (∆EInt), together with the interaction energy of a point charge (ΔEPC) located at the position of Br–´, and its electrostatic component (\( \varDelta {E}_{\mathrm{ES}}^{\mathrm{PC}} \)), plotted as a function of of the Br–Br− distance (R) for the CF3Br•••Br− and CBr4---Br− complexes. Note the much larger contribution from polarization, as defined by the difference \( \varDelta {E}_{\mathrm{Pol}}^{\mathrm{PC}} \)= ΔEPC– \( \varDelta {E}_{\mathrm{ES}}^{\mathrm{PC}} \), in the latter complex

Full size image
Table 1 Equilibrium Br–Br− distance (in Å) and different energy componentsa (in kcal mol–1) of the point charge interaction energy (ΔEPC) and the quantum chemical interaction energy (∆EInt) for the halogen bond complexes
Full size table

Returning to the comparison between ΔEPC and ∆EInt, there is a small but significant difference between the two in the region 3.5 < R < 5 Å, with ∆EInt being lower by at the most 1.5 kcal mol–1 (R = 3.8 Å). This difference can be attributed to contributions from polarization of Br− and dispersion interactions, contributions that are short ranged in nature and that are not accounted for by the PC-model. However, at shorter R, ∆EInt is beginning to level off, and at R = 3.2 Å, ΔEPC becomes lower than ∆EInt. This is partly an effect of charge penetration; the nuclei of CF3Br, in particular Br, penetrate inside the electron density distribution of Br−, resulting in a reduced shielding of the nucleus of Br− and higher Coulombic interaction energy [24, 25]. In addition, there is a repulsive contribution to ∆EInt due to the Pauli antisymmetry requirement. Neither the charge penetration of Br− nor the Pauli repulsion are accounted for by the PC approximation, and hence the lower ΔEPC compared to ∆EInt at small R. In addition, there is the cost of deforming the structure of CF3Br to its geometry in the complex, i.e., ΔENuc−def, which amounts to 1.1 kcal mol–1 and is missing from ΔEPC. At the equilibrium geometry, ΔEPC and ∆EInt differ by 2.1 kcal mol–1, and the values are −15.0 and −12.9 kcal mol–1, respectively.

When comparing the PES of CBr4---Br− and CF3Br•••Br−, there are similarities but also significant differences in the behavior of the different energy terms. First of all, we note that the former interaction is significantly weaker at long R. This is due to a smaller electrostatic contribution to the interaction, i.e., higher \( \varDelta {E}_{\mathrm{ES}}^{\mathrm{PC}} \). However, \( \varDelta {E}_{\mathrm{Pol}}^{\mathrm{PC}} \) is consistently lower than for CF3Br•••Br−, resulting in CBr4---Br− having lower ΔEPC (and ∆EInt) than CF3Br•••Br− at shorter distances. Comparing ΔEPC and ∆EInt of CBr4---Br−, these are again very similar at long R, but diverge in the intermediate region (3.5 < R < 5 Å). Compared to CF3Br•••Br−, the difference between the two energies in this region is larger, which can be attributed to larger contributions to ∆EInt from polarization/induction of Br− and dispersion. Both effects can be attributed to the higher polarizability of CBr4 compared to CF3Br, which results in a stronger dispersion interaction and a higher (induced) dipole moment of CBr4; the induction energy resulting from polarization of Br− is quadratically dependent on the effective dipole moment of the halogen bond donor. The dipole moment of the PC polarized halogen bond donor at the equilibrium geometry of the complex is 3.06 and 3.56 Debye for CF3Br and CBr4, respectively. Potentially, one could also envision a larger charge-transfer contribution to the CBr4---Br− complex, but, as we will discuss later, we find no indication for such a term to be significant in these types of complexes.

At the equilibrium geometry (R = 2.88 Å) of CBr4---Br−, ΔEPC is 1.9 kcal mol–1 lower than ∆EInt. This energy difference is very similar to the corresponding difference (2.1 kcal mol–1) for CF3Br•••Br−. Thus, despite that the PC-model is approximate and only considers electrostatics and polarization, it reproduces the quantum chemical energy difference between the complexes; ΔEPC and ∆EInt of CBr4---Br− are 17.6 and 15.8 kcal mol–1, respectively, whereas the corresponding energies of CF3Br•••Br− are −15.0 and −12.9 kcal mol–1. The results of the PC-model show that the lower complexation energy of CBr4—Br− is entirely due to polarization (\( \varDelta {E}_{\mathrm{Pol}}^{\mathrm{PC}} \)= −9.9 kcal mol–1), as the electrostatic interaction (\( \varDelta {E}_{\mathrm{ES}}^{\mathrm{PC}} \)= −7.7 kcal mol–1) is less favorable than for CF3Br•••Br− (\( \varDelta {E}_{\mathrm{ES}}^{\mathrm{PC}} \)= − 9.61). In the case of CBr4---Br−, \( \varDelta {E}_{\mathrm{Pol}}^{\mathrm{PC}} \) comprises 56% of ΔEPC, which is much higher than the 36% contribution in CF3Br•••Br−. These results can be compared to the EDA results of Head-Gordon and coworkers for the analogous CF3I•••Br− and CBr3I•••Br− complexes [17]. They also found that the substitution of CF3 by CBr3 leads to a significant decrease in ∆EInt. However, whereas Head-Gordon and coworkers attributed this result to charge transfer, our computations unambiguously show that the lower ∆EInt of the brominated compound is a polarization effect.

Electrostatics and polarization determine the halogen bond energy

In Table 1 we list the different energy components of the PC-model together with the full quantum chemical interaction energy (∆EInt) for the entire set of halogen bonded complexes. Optimized geometries of selected complexes are presented in Fig. 2. We first note that the PC-model interaction energy generally is similar, albeit slightly larger, in magnitude to the quantum chemical interaction energy (∆EInt) over the entire data set. There is an excellent linear relationship ∆EInt = 0.88ΔEPC with a correlation coefficient of R2 = 0.9995 and standard error in predicted ∆EInt of 0.29 kcal mol–1, as shown in Fig. 3. It should be remembered that ΔEPC does not consider the cost of deforming the halogen bond donor to its geometry in the complex, and if ΔENuc−def is added to ΔEPC, the proportionality constant increases to 0.92 and R2 decreases only marginally to R2 = 0.9990.

Fig. 2
figure 2

Geometries of some representative complexes computed at the M06-2X/6–311+G(d,p) level of theory. Relevant interatomic distances are given in Angstrom

Full size image
Fig. 3
figure 3

The graph to the left shows the excellent correlation between ∆EInt and ΔEPC for the entire data set of complexes of the types R–Br•••Br− and R´–C≡C-Br•••Br−. The graph to the right shows the corresponding correlation between ∆EInt and \( \varDelta {E}_{\mathrm{ES}}^{\mathrm{PC}} \), where \( \varDelta {E}_{\mathrm{ES}}^{\mathrm{PC}} \) is computed from the electrostatic potential at the position of the Br−. The CF3Br---Br− and CBr4---Br− complexes deviate the most from the correlation and their positions are indicated

Full size image

The almost perfect correlation together with the slope being close to unity and the zero intercept show that the PC-model is able to reproduce the halogen bond interaction energy surprisingly well. The high quality of the correlation is remarkable considering that there are large variations in the chemical environment of the halogen bond donating Br. As indicated in the discussion of the PES of CF3Br•••Br− above, there are energy contributions to ∆EInt that are missing from ΔEPC due to the PC approximation of Br−. However, the correlation equation indicates that the sum of these contributions is a positive energy contribution that varies proportionality to ∆EInt and typically amounts to around 8% of ∆EInt. Thus, our results show that electrostatics and polarization are sufficient to describe the variation in the halogen bond energy, and that charge transfer only has a marginal influence, at most, on the strength of the halogen bond.

Table 1 also lists the electrostatic interaction energy (\( \varDelta {E}_{\mathrm{ES}}^{\mathrm{PC}} \)) and the po larization/induction energy (\( \varDelta {E}_{\mathrm{Pol}}^{\mathrm{PC}} \)) for the entire data set, where the former is computed from the electrostatic potential at the position of Br− and the latter using Eq. (7). Interestingly, the two components are on average of similar size; however, whereas \( \varDelta {E}_{\mathrm{ES}}^{\mathrm{PC}} \) varies between 4 and −18 kcal mol–1, \( \varDelta {E}_{\mathrm{Pol}}^{\mathrm{PC}} \)varies less, and lies with the exception of CBr4---Br− (−9.9 kcal mol–1) in the range of −4 to −8 kcal mol–1. Figure 3 shows that there is a good linear correlation between ∆EInt and \( \varDelta {E}_{\mathrm{ES}}^{\mathrm{PC}} \)(∆EInt = 1.00\( \varDelta {E}_{\mathrm{ES}}^{\mathrm{PC}} \) – 4.7) with an R2 = 0.973. On the basis of this relationship, solely, one could easily make the interpretation that the interaction energy is dominated by electrostatics and has a nearly constant contribution from polarization of around −5 kcal mol–1. However, the rationale for the correlation is not that the polarization contribution is nearly constant, as is obvious from Table 1, but that there is, when CBr4 is excluded, a (weak) linear correlation between \( \varDelta {E}_{\mathrm{Pol}}^{\mathrm{PC}} \) and \( \varDelta {E}_{\mathrm{ES}}^{\mathrm{PC}} \) with an R2 = 0.68. This correlation can partly be explained by that a stronger interaction leads to a shorter Br•••Br distance, which lowers \( \varDelta {E}_{\mathrm{Pol}}^{\mathrm{PC}} \) due to the strong distance dependence of the polarization term. As an example, the weakest complex (NH2CH2Br•••Br−) has a Br–Br distance of 3.45 Å and the strongest (NO2–C≡C–Br•••Br−) a distance of 3.02 Å. However, it should also be recognized that polarization reduces the electron density on the interacting Br and allows for a closer approach of the Br−; an example of this effect is the very short Br•••Br distance (2.88 Å) in CBr4---Br−, which also is the complex that has the lowest \( \varDelta {E}_{\mathrm{Pol}}^{\mathrm{PC}} \) of −9.9 kcal mol–1.

When we analyze the data for the substituted methyl bromide (R–Br) donors, there seems to be a general trend that \( \varDelta {E}_{\mathrm{ES}}^{\mathrm{PC}} \) is determined by the sum of the electron-withdrawing capacities of the substituents, i.e., substituents like F, CN, and NO2 reduce \( \varDelta {E}_{\mathrm{ES}}^{\mathrm{PC}} \) in that order. The \( \varDelta {E}_{\mathrm{ES}}^{\mathrm{PC}} \) of the monosubstituted systems follows the same order as the Hammet σp constant. On the other hand, \( \varDelta {E}_{\mathrm{Pol}}^{\mathrm{PC}} \) decreases with increasing polarizability of the substituents, i.e., in the order H ≈ F < NH2 < CN < NO2 < Br. Although, it may seem trivial that \( \varDelta {E}_{\mathrm{Pol}}^{\mathrm{PC}} \) should follow the polarizability of the substituents, the effect is much larger than would be expected from a through-space interaction, and this large substituent effect is a consequence of the polarization being mediated by the covalent bonds. In the case of CBr4---Br−, the substituent effect on \( \varDelta {E}_{\mathrm{Pol}}^{\mathrm{PC}} \) is larger than anticipated based on an additive contribution from the Br substituents. This can be attributed to the anomeric effect, which is present when several halogens of the same type are bonded to a carbon, and has been described by Clark and coworkers [12, 26].

We now turn to the data of the acetylenic Br donors, i.e., the complexes of the type R´–C≡C–Br. It can first be noted that the electrostatic interaction in general is more favored (\( \varDelta {E}_{\mathrm{ES}}^{\mathrm{PC}} \) is much lower) in comparison with the R–Br donors. This shows that the –C≡C– functionality in itself has a strong electron withdrawing effect. This effect is further augmented by the substituent due to resonance interactions. Resonance electron acceptors generally have a similar quantitative effect on the \( \varDelta {E}_{\mathrm{ES}}^{\mathrm{PC}} \) as the same substituent on the R–Br donors, e.g., a NO2 group lowers \( \varDelta {E}_{\mathrm{ES}}^{\mathrm{PC}} \) by around 10 kcal mol–1 in both systems. Another example of the importance of resonance is the lower \( \varDelta {E}_{\mathrm{ES}}^{\mathrm{PC}} \) of the p-C6H4NO2 substituent compared to a plain phenyl (C6H5) group. However, the effect of the NO2 is only 5 kcal mol–1 and thus half of the effect of an NO2 attached directly to –C≡C–Br. In general, the \( \varDelta {E}_{\mathrm{Pol}}^{\mathrm{PC}} \) values are lower compared to the corresponding values for the R–Br donors. This can mainly be attributed to the R`–C≡C–Br complexes being more stable and having shorter Br–Br distances due to the stronger electrostatic interaction. However, the substituent effects on \( \varDelta {E}_{\mathrm{Pol}}^{\mathrm{PC}} \) are similar in the two types of complexes, with \( \varDelta {E}_{\mathrm{Pol}}^{\mathrm{PC}} \) decreasing with increasing polarizability of the substituent. Also here, we find that the substituent effect on \( \varDelta {E}_{\mathrm{Pol}}^{\mathrm{PC}} \) is mediated via the covalent bonds, and for the R`–C≡C–Br complexes the bond-mediation is enhanced because of the conjugation.

In Table 1, we also list the density deformation energies, \( \varDelta {E}_{\rho -\mathrm{def}}^{\mathrm{PC}} \), and the values follow linear response closely, i.e., \( \varDelta {E}_{\rho -\mathrm{def}}^{\mathrm{PC}}\simeq -\varDelta {E}_{\mathrm{Pol}}^{\mathrm{PC}} \). This supports the interpretation that these interactions are governed by classical electrostatics and polarization. In general, the \( \varDelta {E}_{\rho -\mathrm{def}}^{\mathrm{PC}} \) values are around 0.2 kcal mol–1 lower than the values that would correspond to an exact linear response behavior. This may seem surprising, as nonlinear contributions to the polarization are expected to lead to \( \varDelta {E}_{\rho -\mathrm{def}}^{\mathrm{PC}} \)> −\( \varDelta {E}_{\mathrm{Pol}}^{\mathrm{PC}} \). However, there is also an energy cost (ΔENuc−def) for deforming the geometry of halogen bond donor to its geometry in the complex, and it can be expected that this deformation facilitates the polarization of the halogen bond donor and lowers \( \varDelta {E}_{\mathrm{Pol}}^{\mathrm{PC}} \).

Finally, we turn to the nuclear deformation energy (ΔENuc−def) of the complexes, which varies between 0.1 and 1.3 kcal mol–1. Although, it is difficult to fully rationalize the variation of this quantity, some trends can be observed. First of all, we note, following the discussion of \( \varDelta {E}_{\rho -\mathrm{def}}^{\mathrm{PC}} \) from above, that those complexes which have the largest ΔENuc−def also deviate the most from \( \varDelta {E}_{\rho -\mathrm{def}}^{\mathrm{PC}}=-\varDelta {E}_{\mathrm{Pol}}^{\mathrm{PC}} \). Thus, this supports the hypothesis that a significant driving force for the nuclear deformation is to facilitate polarization and thereby maximize the Coulombic interaction between Br− and the halogen bond donor. Secondly, some substituents, e.g., halogens, NH2, and NO2, generate larger ΔENuc−def values than others, e.g., aromatic substituents and H. Thirdly, the R–Br•••Br− complexes generally have higher values than the corresponding R´–C≡C–Br•••Br− complexes. However, even though the variation in ΔENuc−def is significant, the magnitude of ΔENuc−def is generally small compared to the total interaction energy. This can be seen as a confirmation of the noncovalent character of these complexes, as it can be expected that a significant covalent contribution to the interactions would be accompanied with a larger ΔENuc−def.

Summary and concluding discussion

In this article, we found that the PC-model accurately describes the variations of the halogen bond interaction energy for a diverse group of halogen bond donors and their complexes with Br−. The analysis of the PES of CBr4---Br− and CF3Br•••Br− shows that ∆EInt and ΔEPC are very similar at Br–Br− distances (R) larger than twice the equilibrium distance (Req). In the region 1.8 Req > R > 1.1 Req, ∆EInt is slightly lower than ΔEPC due to energy contributions from polarization of Br− and dispersion. At R < 1.1 Req, ∆EInt begins to level off because of increasing charge penetration and Pauli repulsion. At Req, the sum of the four energy contributions is a positive energy contribution that typically amounts to around 8% of ∆EInt. The remaining part of ∆EInt is determined by ΔEPC with the exception of a small contribution from ΔENuc−def. This is demonstrated by an excellent linear relationship (R2 = 0.999) with a slope of 0.92, and a zero intercept, between ∆EInt and (ΔEPC +ΔENuc−def) for the entire group of halogen bond donors. It should be remembered that charge transfer is completely absent from the PC-model, as there are no electrons than can be transferred to the halogen bond donor. Thus, the results of this study strongly indicate that charge transfer is of negligible importance for halogen bonding.

The analysis of halogen bonding interaction using the PC approximation has the added advantage that the interaction energy can be rigorously separated into electrostatics and polarization. Our results emphasize the important role of polarization in halogen bonding. Within the data set, \( \varDelta {E}_{\mathrm{ES}}^{\mathrm{PC}} \) varies between 4 and −18 kcal mol–1, whereas \( \varDelta {E}_{\mathrm{Pol}}^{\mathrm{PC}} \) varies between −4 and −10 kcal mol–1. In six out of 20 complexes, polarization contributes more strongly than electrostatics to the strength of the halogen bond, i.e., \( \varDelta {E}_{\mathrm{Pol}}^{\mathrm{PC}} \) <\( \varDelta {E}_{\mathrm{ES}}^{\mathrm{PC}} \), and two of these would be unbound without polarization. The analysis further shows that the generally large polarization effect of the studied complexes cannot solely be attributed to the large polarizability of the Br atom, as the polarization is found to be bond-mediated and strongly dependent on the polarizability of the substituents; this effect is particularly pronounced for the R´–C≡C–Br compounds where the bond-mediated polarization is found to be enhanced due to the conjugation. The very low \( \varDelta {E}_{\mathrm{Pol}}^{\mathrm{PC}} \) (−9.9 kcal mol–1) of CBr4---Br− is partly attributed to the anomeric effect that comes from having several Br bonded to the same C. However, despite the resonance enhanced substituent effects on \( \varDelta {E}_{\mathrm{Pol}}^{\mathrm{PC}} \), we found \( \varDelta {E}_{\mathrm{Pol}}^{\mathrm{PC}} \) to follow classical polarization with a linear response behavior with respect to the electric field.

We have shown that the difference in ∆EInt between the CF3Br•••Br− and CBr4---Br− complexes can be unambiguously rationalized in terms of the much lower \( \varDelta {E}_{\mathrm{Pol}}^{\mathrm{PC}} \) of the latter. This is in sharp contrast to the results of Head-Gordon and coworkers on the analogues CF3I•••Br− and CBr3I•••Br− complexes; they found the stronger interaction of the CF3 substituted compound to be the result of a lower charge transfer energy [18]. We can only speculate on the reasons for the discrepancy between the results. It should be noted, however, that in the energy decomposition analysis (EDA) used by Head-Gordon the charge transfer energy is computed as the remaining part of the interaction energy when all other components have been subtracted out. Thus, in the hypothetical case that the EDA is not able to completely describe the polarization effect, the missing part of the polarization energy will end up as a contribution to the charge transfer energy. Another reason for the discrepancy could potentially be that the CX3I•••Br− complexes are very different in their behavior from the CX3Br•••Br− complexes. However, a preliminary analysis using the PC-model confirms that the lower ∆EInt of CBr3I•••Br− compared to CF3I•••Br− is an effect of the stronger polarization in the former complex.

We would also like to comment on the fact that Clark and Heßelmann in their study [12] were able to correlate ∆EInt with the surface electrostatic potential maximum obtained from the polarized density alone, whereas Eq. 3 shows that the (unpolarized) electrostatic potential and the polarized potential contribute equally by a factor of 0.5 to the interaction energy. The reason for the successful correlation is probably the relatively small variation in the surface electrostatic potential maximum among the studied halogen bond donors in their study, and thus it is likely that the influence of the (average) electrostatic potential is accounted for by the intercept. It is indeed noteworthy that the slope of 0.43 in front of the polarized potential in the Clark and Heßelmann study is very similar to our proportionality constant of 0.88, from the ∆EInt and ΔEPC correlation, multiplied by the factor 0.5.

Finally, we would like to emphasize the advantage of using simple and at the same time physically relevant models when analyzing intermolecular interactions. In this study, charge transfer could be ruled out, as the PC-model accurately reproduces the halogen bond energy without having electrons that can be transferred. Furthermore, we were able to rigorously separate electrostatics from polarization and thereby demonstrate the high importance of polarization for the halogen bond. In an upcoming study we intend to use the same approach to investigate the character of the hydrogen bond to shed light upon the differences and similarities of halogen and hydrogen bonding.