1 Introduction

Risk measures constitute one of the most active areas of research in financial mathematics, for they provide a general axiomatic framework to assess risks. Their universality and wide applicability, together with the wealth of related interesting mathematical questions, have led to considerable theoretical and applied developments; see, among others, [1, 11] and [10, Chap. 4] with more references therein, and [3, 6, 21, 34] for dynamic convex risk measures.

A number of popular risk measures are defined in relation to investment opportunities in a financial market like, for example, VaR, CVaR, indifference prices, etc. However, such measures are directly tied to a specific trading horizon, for it is implicitly assumed that every risk position will be introduced and mature at times (random or not) up to this pre-chosen horizon. We refer the reader to [36, Sect. 3.3] for motivational examples and detailed discussions. Such issues motivated the authors of [36] to introduce the so-called maturity-independent risk measures (Definition 3.1 therein). These measures were defined axiomatically, in relation to a general semimartingale market, via four fundamental properties: anti-positivity, convexity, cash translativity and replication invariance.

An important class of maturity-independent risk measures are the forward entropic risk measures, which were constructed as (negative) indifference prices under exponential forward performance criteria (see Definition 3.1). Forward performance criteria are quite appropriate to define dynamic risk measures that do not depend on a specific horizon or maturity, since the underlying forward performance processes are defined for all times. As a result, they can be suitably used to assess the performance of investment strategies with and without the (arbitrary) risk positions, no matter when these positions are introduced or mature. For general semimartingale models, an implicit form for forward entropic risk measures was derived in [36] (cf. (4.14) therein) via the solution of a forward stochastic optimization problem.

Herein, we build on the work of [36], focusing on incomplete market models with multiple stocks and multiple stochastic factors, and working with forward performance processes that are deterministic functions of these factors. This is a rich class of criteria that not only offer tractability in constructing and further studying the forward risk measures, but also enable us to make interesting connections with ergodic backward stochastic differential equations (BSDEs).

Markovian forward performance criteria in stochastic factor models were studied in [32], where the multi-stock/multi-factor complete market case was solved. The incomplete market case with a single stock/single factor was examined in [33] and in [35] for a model with slow and fast stochastic factors, and more recently in [23].

While we look at a smaller class of market models than those considered in [36], our setting is more general in two directions. Firstly, we incorporate trading constraints. This not only makes the analysis more involved but, more importantly, results in violation of the replication invariance property (see discussions after Corollary 3.6). Secondly, we consider and analyze in detail the forward risk measure process, while the authors of [36] only provided the risk measure at a single time, through an implicit forward optimization problem.

Our contribution is multifold. Firstly, we study the explicit representation of the forward entropic risk measure process in Theorem 3.2. To obtain it, we need to solve two forward stochastic optimization problems, with and without the risk position for an arbitrary trading horizon associated with the maturity of the (arbitrary) risk position. The solution of the latter problem is given directly by the exponential forward performance process itself, but it is not a priori clear how to solve the former, even if we interpret it as a classical expected utility problem with random endowment. This is due to the presence of additional terms that violate standard boundedness or integrability conditions. As a consequence, classical results in expected utility theory do not apply (see discussions after Definition 3.1). Instead, we use an alternative approach, based on the recent work of [23] on the construction of homothetic (exponential, power and logarithmic) forward performance processes using ergodic BSDEs. This method bypasses a number of technical difficulties associated with solving an underlying ill-posed stochastic partial differential equation (SPDE) that the forward performance process is expected to satisfy; see [7] and [31] for discussions on this forward SPDE.

For the exponential family we consider herein, the approach in [23] yields a unique representation of the forward performance criterion in a factor form (Proposition 2.6). Based on this result, we establish in Theorem 3.2 that the forward entropic risk measure satisfies a BSDE whose driver depends on the solution of the ergodic BSDE for the forward performance process.

From this BSDE representation, we establish the following results. Firstly, using the convexity property of its driver, we derive a convex dual representation of the forward entropic risk measure (Theorem 3.5). Specifically, we show that the forward entropic risk measure is the minimal, among all equivalent probability measures, expected value of the risk position plus a penalty term. The penalty term has the following properties: it is independent of both the risk position and its maturity. Rather, it depends exclusively on the stochastic factors and the solution to the aforementioned ergodic BSDE.

The dual representation result readily yields that the three properties—anti-positivity, convexity and cash translativity—that were introduced in [36] indeed hold. It also demonstrates that because of trading constraints, the replication invariance property fails. If the constraints are removed, this property naturally holds; this can also be seen in the example in Sect. 4, where the equivalent probability measures turn out to be equivalent martingale measures.

In a different direction, we derive a parity result between the forward and classical entropic risk measures. We show that the former can be constructed as the difference of two classical entropic risk measures applied, respectively, to a modified risk position and a normalizing factor related to the solution of the ergodic BSDE for the forward performance process.

We also study the asymptotic behavior of the forward entropic risk measures when their maturity is long (Theorem 3.10). For risk positions given by deterministic functions of the stochastic factor processes, we show that their risk measures converge to a constant which is independent of the initial state of the stochastic factors, and furthermore, the convergence is exponentially fast. We also derive an explicit exponential bound of the associated hedging strategies, which in turn yields that as the maturity goes to infinity, no trading occurs in any finite time to hedge the underlying risks.

We conclude with an example cast in the single stock/single stochastic factor case. Using the ergodic BSDE approach, we derive a closed form representation of the forward entropic risk measure and its convex dual representation. We also derive a representation of its classical analogue, and in turn compute numerically the long-term limits of the two measures for specific risk positions.

The paper is organized as follows. In Sect. 2, we introduce the stochastic factor market model and provide background results on exponential forward performance processes. In Sect. 3, we provide the definition of the forward entropic risk measures, derive their representation results and also establish the parity with their classical counterparts. We also study the long-maturity behavior. We present an example in Sect. 4 and conclude in Sect. 6. For the reader’s convenience, the proofs of the main results are presented separately in Sect. 5.

2 The investment model and the performance criterion

Let \(W\) be a \(d\)-dimensional Brownian motion on a probability space \((\Omega ,\mathcal{F},\mathbb{P})\). Denote by \(\mathbb{F}=( \mathcal {F}_{t})_{t\geq 0}\) the augmented filtration generated by \(W\). We consider a market with a risk-free bond offering zero interest rate and \(n\) risky stocks, with \(n\leq d\).

The stock price processes \(S^{i}\), \(i=1,\ldots,n\), solve

$$ \frac{dS_{t}^{i}}{S_{t}^{i}}=b^{i}(V_{t})dt+\sigma^{i}(V_{t})dW_{t}, $$

with \(b^{i}:\mathbb{R}^{d}\rightarrow\mathbb{R},\sigma^{i}:\mathbb{R} ^{d}\rightarrow\mathbb{R}^{1\times d}\) and \(S_{0}^{i}={s_{0}^{i}}>0\).

The stochastic factor process \(V\) is \(d\)-dimensional and solves

$$ dV_{t}=\eta(V_{t})dt+\kappa dW_{t}, $$
(2.1)

with \(\eta:\mathbb{R}^{d}\rightarrow\mathbb{R}^{d},\kappa\in\mathbb{R} ^{d\times d}\) and \(V_{0}=v\), \(v\in\mathbb{R}^{d}\).

We introduce the following model assumptions. Throughout, we use \(A^{\mathrm{tr}}\) for the transpose of a matrix \(A\), and whenever needed, the self-evident notation \(V^{v}\) for the stochastic factor process \(V\) starting from \(V_{0}=v\).

Assumption 2.1

(i) The drift and volatility coefficients \(b^{i}(v) \) and \(\sigma^{i}(v)\), \(v\in\mathbb{R}^{d}\), are uniformly bounded.

(ii) The volatility matrix \(\sigma(v):=(\sigma^{1}(v),\ldots ,\sigma^{n}(v))^{\mathrm{tr}}\), \(v\in\mathbb{R}^{d}\), has full row rank \(n\).

(iii) The market price of risk

$$ \theta(v):=\sigma(v)^{\mathrm{tr}}\big(\sigma(v)\sigma(v)^{\mathrm{tr}}\big)^{-1}b(v), $$
(2.2)

\(v\in\mathbb{R}^{d}\), is uniformly bounded and Lipschitz-continuous.

Assumption 2.2

(i) The coefficient \(\eta(v) \) satisfies a dissipativity condition, namely, there exists a large enough constant \(C_{\eta}>0\) such that for \(v,\bar{v}\in\mathbb{R}^{d}\),

$$ \big( \eta( v) -\eta( \bar{v}) \big) ^{\mathrm{tr}}( v-\bar{v}) \leq-C_{\eta} \vert v-\bar{v} \vert^{2}. $$
(2.3)

(ii) The matrix \(\kappa\) is positive definite and normalized to \(\vert\kappa\vert=1\).

The “large enough” property of \(C_{\eta}\) in Assumption 2.2(i) will be quantified in the sequel when it is assumed that \(C_{\eta }>C_{v}>0\), where \(C_{v}\) appears in the properties of the driver of an upcoming ergodic BSDE (see inequality (5.1)).

The assumption that the matrix \(\kappa\) is constant is without loss of generality as long as the more general case \(\kappa=\kappa(v) \) satisfies the uniform ellipticity condition. This condition is crucial for establishing the coupling estimate (2.5) that will be frequently used. The case where \(\kappa (v) \) is degenerate is far more challenging and left for future research.

Proposition 2.3

Under Assumption 2.2, the following assertions hold:

(i) The stochastic factor process satisfies, for\(v,\bar{v}\in \mathbb{R} ^{d}\), \(t\geq0\),

$$ |V_{t}^{v}-V_{t}^{\bar{v}}|^{2}\leq e^{-2C_{\eta}\,t}|v-\bar{v}|^{2}. $$

(ii) Assume that the process\(V^{v}\)follows

$$ dV_{t}^{v}=\big( \eta(V_{t}^{v})+H(V_{t}^{v})\big) dt+\kappa dW_{t}^{H}, $$

where\(H:\mathbb{R}^{d}\rightarrow\mathbb{R}^{d}\)is a bounded measurable function, \(\mathbb{Q}^{H}\)is a probability measure equivalent to ℙ, and\(W^{H}\)is a\(\mathbb{Q}^{H}\)-Brownian motion. Then there exists a constant\(C>0\)such that

$$ E_{{\mathbb{Q}^{H}}}\big[ |V_{t}^{v}|^{p}\big] \leq C( 1+|v|^{p}) $$
(2.4)

for any\(p\geq1\). Furthermore, for any measurable function\(\phi: \mathbb{R}^{d}\rightarrow\mathbb{R}\)with polynomial growth rate\(\mu>0\)and\(v,\bar{v}\in\mathbb{R}^{d}\),

$$ \vert E_{{\mathbb{Q}^{H}}}[ \phi(V_{t}^{v})-\phi(V_{t}^{\bar{v} })] \vert\leq C( 1+|v|^{1+\mu}+|\bar{v}|^{1+\mu }) e^{-\hat{C}_{\eta}\,t}. $$
(2.5)

The constants\(C\)and\(\hat{C}_{\eta}\)depend on the function\(H(\cdot)\)only through\(\sup_{v\in\mathbb{R}^{d}}|H(v)|\).

The proof of (i) follows from Gronwall’s inequality. Inequality (2.4) is an application of a Lyapunov argument (see [9, Lemma 3.1]), while inequality (2.5) follows from the coupling estimate in [19, Lemma 3.4].

Proposition 2.3 implies that the stochastic factor process \(V\) admits a unique invariant measure and is thus ergodic. Moreover, any two paths converge to each other exponentially fast.

2.1 The trading strategies

In this market environment, an investor trades dynamically among the bond and the stocks. Let \(\tilde{\pi}=(\tilde{\pi}^{1},\ldots,\tilde{\pi} ^{n})^{\mathrm{tr}}\) and \(\pi^{0}\) denote the (discounted by the bond) amounts in the stocks and bond, respectively. The investor’s total wealth (discounted by the bond) is given by \(X_{t}^{\tilde{\pi}}=\pi_{t}^{0}+\Sigma_{i=1}^{n} \tilde{\pi}_{t}^{i}\), \(t\geq0\). The investment strategies are taken to be self-financing, and thus \(X_{t}^{\tilde{\pi}}\) satisfies

$$ dX_{t}^{\tilde{\pi}}=\sum_{i=1}^{n}\frac{\tilde{\pi}_{t}^{i}}{S_{t}^{i}} dS_{t}^{i}=\tilde{\pi}_{t}^{\mathrm{tr}}\sigma(V_{t})\big( \theta (V_{t})dt+dW_{t}\big) , $$

with \(X_{0}=x\in\mathbb{R}\) and \(\theta\) defined in (2.2). As in [23], we work with investment strategies rescaled by the volatility, \(\pi_{t}^{\mathrm{tr}}:=\tilde{\pi}_{t}^{\mathrm{tr}}\sigma(V_{t})\in \mathbb{R} ^{1\times d}\), yielding

$$ dX_{t}^{\pi}=\pi_{t}^{\mathrm{tr}}\big( \theta(V_{t})dt+dW_{t}\big). $$
(2.6)

The investor invests under trading constraints for her strategies, namely, we assume that \(\pi_{t}\in\Pi\) with \(\Pi\) being a closed and convex subset in \(\mathbb{R}^{d}\), including the origin. For each \(t\geq0\), we denote by \(\mathcal{A}_{[0,t]}\) the set of admissible investment strategies on \([0,t]\), defined as

$$ \mathcal{A}_{[0,t]}=\{ \pi\in\mathcal{L}_{\mathrm{BMO}}^{2}[0,t]: \pi_{s}\in \Pi , s\in[0,t]\} , $$

where

$$\begin{aligned} \mathcal{L}_{\mathrm{BMO}}^{2}[0,t]:=\big\{ (\pi_{s})_{s\in[0,t]} : &\text{ $\pi$ is $ \mathbb{F}$-progressively measurable and} \\ &\text{ $\textstyle E_{\mathbb{P}}\big[ \int_{\tau}^{t}|\pi _{s}|^{2}ds\big\vert \mathcal{F}_{\tau}\big] \leq C$ $\mathbb{P}$-a.s.} \\ & \text{ for some constant $C$ and all $\mathbb{F}$-stopping times $\tau\le t$}\big\} . \end{aligned}$$

For each \(s\in[0,t] \), the admissible set \(\mathcal{A} _{[s,t]}\) is defined in a similar way. We also introduce \(\mathcal {A}:=\bigcup _{t\geq0}\mathcal{A}_{[0,t]}\), the set of admissible investment strategies for all\(t\geq0\).

2.2 The forward performance criterion

The investor uses an exponential forward performance criterion to measure the performance for her investment strategies. For the reader’s convenience, we start with some background results about this criterion, first recalling its definition (see [26,27,28,29,30]). We then focus on the exponential class and review its ergodic BSDE representation established in [23].

Definition 2.4

Let \(\mathbb{D=R}\times[ 0,\infty)\). A process \(U(x,t) \), \((x,t) \in \mathbb{D}\), is a forward performance process if

(i) for each \(x\in\mathbb{R}\), \(U(x,t) \) is \(\mathbb{F}\)-progressively measurable;

(ii) for each \(t\geq0\), the mapping \(x\mapsto U(x,t)\) is strictly increasing and strictly concave;

(iii) for all \(\pi\in\mathcal{A}\) and \(0\leq t\leq s\),

$$ U( X_{t}^{\pi},t) \geq E_{\mathbb{P}}[ U(X_{s}^{\pi},s)\vert\mathcal{F} _{t}] , $$

and there exists an optimal \(\pi^{\ast}\in\mathcal{A}\) such that

$$ U( X_{t}^{\pi^{\ast}},t) =E_{\mathbb{P}}[ U(X_{s}^{\pi^{\ast }},s)\vert \mathcal{F}_{t}] , $$

with \(X^{\pi},X^{\pi^{\ast}}\) solving (2.6).

Herein, we focus on Markovian exponential forward performance criteria, namely, processes that are deterministic functions of the stochastic factors,

$$ U ( x,t) =-e^{-\gamma x+f(V_{t},t)}, $$
(2.7)

for \((x,t)\in\mathbb{D}\) and \(\gamma>0\) and appropriate function(s) \(f:\mathbb{R}^{d}\times[ 0,\infty) \rightarrow\mathbb{R}\).

There are two approaches in specifying the process \(f( V_{t},t)\). One may try to determine the function(s) \(f( \cdot,\cdot) \) using a (deterministic) PDE that they are expected to satisfy. The form of this equation follows from imposing on the candidate solutions (2.7) the supermartingale and martingale conditions in part (iii) above (see [23]; also [31] and [32]). However, this PDE is ill-posed, and as a consequence, there are various difficulties and open questions for its solution(s).

Alternatively, one may specify the process \(f( V_{t},t) \) directly. This was done in [23], where the authors developed a probabilistic approach based on ergodic BSDEs (see [4, 5, 12, 19, 23] for recent developments of ergodic BSDEs). They showed that the forward performance process of the form (2.7) exists and furthermore derived its explicit representation using the solution of an ergodic BSDE. For the reader’s convenience, we briefly review these results next.

Proposition 2.5

([23, Proposition 4.1])

Suppose that Assumptions 2.1and 2.2hold. Then the ergodic BSDE

$$ dY_{t}=\big(-F(V_{t},Z_{t})+\lambda\big)dt+Z_{t}^{\mathrm{tr}}dW_{t}, $$
(2.8)

where the driver\(F:\mathbb{R}^{d}\times\mathbb{R}^{d}\rightarrow \mathbb{R} \)is defined as

$$ F(v,z)=\frac{1}{2}\gamma^{2}\mathrm{dist}^{2}\bigg(\Pi,\frac{\theta (v)+z}{\gamma}\bigg) -\frac{1}{2}|\theta(v)+z|^{2}+\frac{1}{2}|z|^{2}, $$
(2.9)

with\(\theta(\cdot)\)as in (2.2), admits a unique Markovian solution\((Y_{t},Z_{t},\lambda)\), \(t\geq0\). Specifically, there exist a unique\(\lambda\in\mathbb{R}\)and functions\(y:\mathbb{R}^{d}\rightarrow\mathbb{R}\)and\(z:\mathbb{R}^{d}\rightarrow\mathbb{R}^{d}\)such that

$$ ( Y_{t},Z_{t}) =\big( y ( V_{t}) ,z( V_{t}) \big) . $$
(2.10)

The function\(y(\cdot)\)is unique up to an additive constant, and without loss of generality, we can set\(y(0)=0\). Moreover, \(y(\cdot)\)has at most linear growth and satisfies

$$ |\nabla y(v)|\leq\frac{C_{v}}{C_{\eta}-C_{v}}, $$
(2.11)

and\(z(\cdot)\)is bounded with\(|z(\cdot)|\leq\frac{C_{v}}{C_{\eta }-C_{v}}\), where the constants\(C_{\eta}\)and\(C_{v}\)are as in Assumption 2.2and inequality (5.1), respectively.

As shown in [23], the form of the driver \(F\) is dictated by the martingale and supermartingale requirements (see part (iii) in Definition 2.4) that the candidate forward performance process must satisfy. In Sect. 4, we provide a specific example for this driver. We also refer the reader to [23, Sect. 3.1.2] for the connection of \(F\) with the ill-posed PDE that the function \(f(\cdot,\cdot)\) in (2.7) solves.

The next result relates the above unique Markovian solution of the ergodic BSDE (2.8) to the Markovian exponential forward performance process (2.7) and its associated optimal policy. For its proof, see [23, Theorem 4.2].

Proposition 2.6

([23, Theorem 4.2])

Suppose that Assumptions 2.1and 2.2hold, and let\((Y,Z,\lambda)\)be the unique Markovian solution to the ergodic BSDE (2.8). Then the process\(U(x,t)\), \((x,t) \in\mathbb{D}\), given by

$$ U(x,t)=-e^{-\gamma x+}{}^{Y_{t}-\lambda t} $$
(2.12)

is an exponential forward performance process. It solves

$$ dU(x,t)=-U(x,t)\bigg( F(V_{t},Z_{t})+\frac{1}{2}|Z_{t}|^{2}\bigg) dt+U(x,t)Z_{t}^{\mathrm{tr}}dW_{t}. $$
(2.13)

Furthermore, the associated optimal strategy is given by

$$ \pi_{t}^{\ast}=\mathrm{Proj}_{\Pi}\left( \frac{\theta(V_{t})+Z_{t} }{\gamma}\right) . $$
(2.14)

From (2.13), we may identify the process \(Z\) with the volatility component of the forward performance criterion. We also remark that the volatility term in the Itô decomposition of \(U(x,t) \) is not zero, and thus \(U(x,t) \) is not monotone with respect to time.

Remark 2.7

In [23], the solution pair \((Y,Z)\) is constructed by a “vanishing discount rate” argument, i.e., the components of \((Y,Z)\) are the limiting processes, as \(\rho\downarrow0\), of the solution to an infinite-horizon BSDE with a discount factor \(\rho\). Furthermore, the constant \(\lambda\) can be interpreted as the long term growth rate of a classical exponential utility maximization problem (see [23, Proposition 3.3]).

Remark 2.8

Forward performance processes are not unique. For example, within the exponential class, a time-monotone forward performance process is given by

$$ U_{0} ( x,t) =-e^{-\gamma x+\frac{1}{2}A_{t}}, $$

with \(A_{t}>0\) being a nondecreasing process that is path-dependent on the stochastic factors. Furthermore, an extended class is given by

$$ U_{0}^{ ( M,N) } ( x,t) =-M_{t}\exp\left( -\frac{\gamma x}{N_{t}}+\frac{1}{2}A_{t}^{( M,N) }\right) , $$

with \(M,N\) and \({A^{(M,N) }}\) representing a market view, a benchmark and a stochastic time change (see [29, 37]). We stress, however, that the forward performance process in the stochastic factor form (2.7) cannot be generated using processes like \(U_{0}^{(M,N)}(x,t) \) by merely manipulating the benchmark and market view processes, because once \(M\) and/or \(N\) is introduced, the market is no longer the original one. Secondly, even if \(M=N= 0\), and we are thus in the original market, it is not possible to convert the path-dependent time-monotone process \(U_{0}(x,t) \) to a non-path-dependent process of the form (2.7). We refer the reader to [23] for a detailed discussion on the above issues.

3 Forward entropic risk measures

We introduce and study dynamic forward entropic risk measures in relation to the exponential forward performance process (2.12). We consider risk positions in a general space ℒ, defined as

$$ \mathcal{L}=\bigcup_{T\geq0}\mathcal{L}^{\infty}( \mathcal{F} _{T}) , $$

where \(\mathcal{L}^{\infty}(\mathcal{F}_{T})\) is for each \(T>0\) the space of uniformly bounded \(\mathcal{F}_{T}\)-measurable random variables.

Definition 3.1

Consider the Markovian forward exponential performance process \(U(x,t) =-e^{-\gamma x+}{}^{Y_{t}-\lambda t}\), \((x,t)\in\mathbb{D}\) (cf. (2.12)).

(i) Let \(T>0\) be an arbitrary horizon and consider a risk position \(\xi \in \mathcal{L}^{\infty}( \mathcal{F}_{T}) \). Its \(T\)-normalized forward entropic risk measure, denoted by \(\rho_{t}(\xi;T)\in\mathcal {F}_{t}\), is defined for \(t\in[ 0,T] \) via

$$ U( x,t) ={u}^{\xi}\big(x+\rho_{t}(\xi;T),t\big) $$
(3.1)

for all \(( x,t) \in\mathbb{R}\times[0,T]\), where

$$ {u}^{\xi}(x,t):=\mathop{\mathrm{ess}\,\mathrm{sup}}_{\pi\in\mathcal{A}_{[t,T]}}E_{\mathbb{P}} \bigg[ U\bigg(x+\int_{t}^{T}\pi_{s}^{\mathrm{tr}}\big( \theta (V_{s})ds+dW_{s}\big) +\xi,T\bigg)\bigg\vert \mathcal{F}_{t}\bigg] . $$
(3.2)

(ii) Consider an arbitrary risk position \(\xi\in\mathcal{L}\) and define its maturity

$$ T:=\inf\{ t\geq0:\xi\text{ is }\mathcal{F}_{t}\text{-measurable}\} $$

so that \(\xi\in\mathcal{L}^{\infty}(\mathcal{F}_{T})\). Then its forward entropic risk measure, denoted by \(\rho_{t}(\xi)\), is defined, for \(t\in[ 0,T] \), as

$$ \rho_{t}(\xi):=\rho_{t}(\xi;T). $$
(3.3)

Definition (3.3) highlights the independence of the risk measure operator \(\rho_{t}(\cdot)\) on both the maturity and the trading horizon. Obviously, for each risk position \(\xi\), \(\rho_{t}(\xi)\) depends on the size of \(\xi\) and \(T\). But the operator per se is constructed through (3.1) and (3.2), which are defined for any maturity \(T\) since the underlying forward performance criterion is defined for all times \(t\geq0\).

The next task is to calculate the forward entropic risk measure from the “indifference-type” condition (3.1). The left-hand side is already known from (2.12). Using the form in (2.12), we can also view (3.2) as a classical expected utility maximization problem with random endowment \(\bar{\xi}_{T}:=\xi-\frac{Y_{T}-\lambda T}{\gamma}\), namely

$$ {u}^{\xi}(x,t)=\mathop{\mathrm{ess}\,\mathrm{sup}}_{\pi\in\mathcal{A}_{[t,T]}}E_{\mathbb{P}} \bigg[ -e^{-\gamma( x+\int_{t}^{T}\pi_{s}^{\mathrm{tr}}( \theta (V_{s})ds+dW_{s}) +\bar{\xi}_{T}) }\bigg\vert \mathcal{F}_{t} \bigg] . $$

Note, however, that the random variable \(\bar{\xi}_{T}\) is in general neither bounded nor exponentially integrable and hence classical results on exponential utility optimization (see for example [16, 18]) may not apply. This motivated the development of an alternative solution approach, presented next.

3.1 BSDE representation of forward entropic risk measures

We provide here the first main result, which is the representation of the forward entropic risk measure process using finite horizon BSDEs and ergodic BSDEs. We show that the risk measure process of an arbitrary maturity, say \(T>0\), can be constructed as the solution of a BSDE on \([ 0,T]\), with its driver depending on the process \(Z\) of the solution to the ergodic BSDE (2.8). This dependence emerges because the ergodic BSDE (2.8) was used to construct the forward performance criterion (2.12) appearing in (3.1) of Definition 3.1.

Theorem 3.2

Consider an arbitrary risk position\(\xi\in\mathcal{L}\)with maturity\(T\). Suppose that Assumptions 2.1and 2.2hold. Introduce for\(t\in[ 0,T] \)the BSDE

$$ Y_{t}^{{\xi}}=\xi+\int_{t}^{T}G(V_{u},Z_{u},Z_{u}^{\xi })du-\int_{t}^{T}(Z_{u}^{\xi})^{\mathrm{tr}}dW_{u}, $$
(3.4)

with the driver\(G:\mathbb{R}^{d}\times\mathbb{R}^{d}\times\mathbb{R} ^{d}\rightarrow\mathbb{R}\)defined as

$$ G(v,{z},\bar{z})=\frac{1}{\gamma}\big( F(v,{z}+\gamma\bar{z})-F(v,{z} )\big) , $$
(3.5)

where\(F\)is as in (2.9) and the process\(Z\)is the second component of the solution (2.10) of the ergodic BSDE (2.8). Then the following assertions hold:

i) The BSDE (3.4) has a unique solution\(( Y_{t}^{\xi},Z_{t}^{\xi}) \), \(t\in[ 0,T] \), with\(Y^{\xi } \)being uniformly bounded and\(Z^{\xi}\in\mathcal{L}_{\mathrm{BMO}}^{2}[0,T]\).

ii) The forward entropic risk measure of\(\xi\)is given, for\(t\in[ 0,T] \), by

$$ \rho_{t}(\xi)=Y_{t}^{-\xi}. $$
(3.6)

An immediate consequence of the above representation is the dynamic consistency property of the forward entropic risk measures.

Corollary 3.3

Consider an arbitrary risk position\(\xi\in\mathcal{L}\)with maturity\(T\). Suppose that Assumptions 2.1and 2.2hold. Then for\(0\leq t\leq s\leq T\), its forward entropic risk measure satisfies

$$ \rho_{t}(\xi)={\rho_{t}\big(-\rho_{s}(\xi)\big)}. $$

The above property follows directly from (3.6) and the fact that the solution of (3.4) satisfies \(Y_{t}^{-\xi}=Y_{t}^{Y_{s}^{-\xi}}=Y_{t}^{\rho_{s}( \xi ) }\), for \(0\leq t\leq s\leq T\).

The fact that the forward entropic risk measure is represented as the solution of a finite horizon BSDE is not surprising since given an arbitrary maturity, the “indifference-type” condition (3.1) is by nature set “backwards” in time. There are, however, two fundamental differences between the BSDEs for classical and forward entropic risk measures. Firstly, the BSDE (3.4) differs from its classical counterpart since its driver \(G\) depends on the process \(Z\) related to the solution of the ergodic BSDE. Thus the two BSDEs do not coincide, and as a result, they produce different solutions within the common horizon \([ 0,T] \). This is, for example, reflected below in the parity result (3.13) between the forward and classical entropic risk measures. Secondly, the BSDE for the classical entropic risk measure is defined only for a preset investment horizon \([ 0,T] \), for some single, fixed \(T\). In contrast, in the forward setting, the BSDE (3.4) is set for any arbitrary interval \([ 0,T] \), associated with the maturity \(T\) of the arbitrary risk position \(\xi\).

Besides defining the forward entropic risk measure of a risk position, one may also introduce the associated forward hedging strategies. As in the classical case, they are defined as the difference between the optimal strategies with and without the risk position. The former is the optimal strategy for (3.2), provided in the sequel (see (5.5)), while the latter was derived in (2.14).

Corollary 3.4

Consider an arbitrary risk position\(\xi \in\mathcal{L}\)with maturity\(T\). Suppose that Assumptions 2.1and 2.2hold. Then the associated hedging strategy\(\alpha_{t,T}\)for\(t\in [0,T]\)is given by

$$\begin{aligned} \alpha_{t,T}&:={\pi}_{t}^{\ast,{\xi}}-{\pi}_{t}^{\ast} \\ &\phantom{:}=\mathrm{Proj}_{\Pi}\left({Z_{t}^{-\xi}}+\frac{\theta (V_{t})+Z_{t}}{\gamma}\right) -\mathrm{Proj}_{\Pi} \left( \frac{\theta(V_{t})+Z_{t}}{\gamma}\right) . \end{aligned}$$

Observe that the hedging strategy naturally depends on the maturity of the risk position in consideration only through the first term \({\pi}_{t}^{\ast,{\xi}}\), and in particular through the process \(Z^{-{\xi}}\). The second term, the optimal policy of \(U( x,t) \), \(t\geq0\), is independent of both the claim and its maturity. This is not the case in the classical setting, where both terms depend on the investment horizon of the underlying exponential utility maximization problems (see for instance [16]).

3.2 Convex dual representation of forward entropic risk measures

The second main result is an alternative representation of the forward entropic risk measure using convex duality arguments. Using that the set of portfolio constraints \(\Pi\) is convex and a distance function to a convex set is also convex, it follows that the driver \(G(v,z,\bar{z})\) defined in (3.5) is convex in \(\bar{z}\), for any \((v,z)\in\mathbb {R}^{d}\times \mathbb{R}^{d}\). We can therefore introduce the convex dual of \(G(v,z,\cdot)\),

$$ {\hat{G}}(v,z,p):=\sup_{\bar{z}\in\mathbb{R}^{d}}\big( \bar{z}^{\mathrm{tr}}p-G(v,z,\bar{z})\big) , $$
(3.7)

for \(p\in\mathbb{R}^{d}\). Note that \(\hat{G}\) is valued in \(\mathbb{R}\cup\{ \infty\}\). Then the Fenchel–Moreau theorem yields that for \(\bar{z}\in{\mathbb{R}^{d}}\),

$$ G(v,z,\bar{z})=\sup_{p\in\mathbb{R}^{d}}\big(\bar{z}^{\mathrm{tr}}p-\hat {G}(v,z,p)\big). $$
(3.8)

Moreover, the maximizer in (3.8) exists, i.e., there exists \(p^{\ast }\in \partial G_{\bar{z}}(v,z,\bar{z})\), the sub-differential of \(\bar {z}\mapsto G(v,z,\bar{z})\) at \(\bar{z}\in{\mathbb{R}^{d}}\), such that

$$ G(v,z,\bar{z})=\bar{z}^{\mathrm{tr}}p^{\ast}-\hat{G}(v,z,p^{\ast}). $$
(3.9)

Let \(\xi\in\mathcal{L}\) be an arbitrary risk position with maturity \(T\). For this (arbitrary) \(T\), consider the set of density processes \(q\in \mathcal{L}_{\mathrm{BMO}}^{2}[0,T]\). For each such \(q\), the stochastic exponential \(\mathcal{E}(\int_{0}^{\cdot}q_{s}^{\mathrm{tr}}dW_{s})\) is a uniformly integrable martingale since \(\int_{0}^{\cdot}q_{s}^{\mathrm{tr}}dW_{s}\) is a BMO-martingale. We define by \(\frac{d\mathbb{Q}^{q}}{d\mathbb{P}}|_{\mathcal{F}_{T}}=\mathcal{E} (\int_{0}^{\cdot}q_{s}^{\mathrm{tr}}dW_{s})_{T}\) a probability measure \(\mathbb{Q}^{q}\) on \({\mathcal{F}_{T}}\) and introduce for each \(t\in [ 0,T] \) the set of admissible density processes,

$$ \mathcal{A}_{[t,T]}^{\prime}:=\bigg\{ q\in\mathcal{L}_{\mathrm{BMO}}^{2}[t,T]: E_{\mathbb{Q}^{q}}\bigg[ \int_{t}^{T}|\hat{G}(V_{u},Z_{u},q_{u})|du \bigg\vert \mathcal{F}_{t}\bigg] < \infty\bigg\} , $$
(3.10)

with \(V\) solving (2.1) and \(Z\) as in (2.10) for the ergodic BSDE (2.8).

Theorem 3.5

Consider an arbitrary risk position\(\xi\in \mathcal{L}\)with maturity\(T\). Suppose that Assumptions 2.1and2.2hold. Then for\(t\in[ 0,T] \), the following assertions hold:

(i) The forward entropic risk measure\(\rho_{t}(\xi)\)admits the convex dual representation

$$ \rho_{t}(\xi)=-\mathop{\mathrm{ess}\,\mathrm{inf}}_{q\in\mathcal{A}_{[t,T]}^{\prime}}E_{\mathbb {Q}^{q}}\bigg[ \xi+\int_{t}^{T}{\hat{G}}(V_{s},Z_{s},q_{s})ds \bigg\vert \mathcal{F}_{t}\bigg] , $$
(3.11)

where\({\hat{G}}:\mathbb{R}^{d}\times\mathbb{R}^{d}\times\mathbb{R} ^{d}\rightarrow\mathbb{R}\cup\{ \infty\}\), the convex dual of the driver\(G \), is defined in (3.7), and the process\(Z\)is the second component in the solution of the ergodic BSDE (2.8).

(ii) There exists an optimal density process\(q^{\ast,\xi}\in \mathcal{A} _{[t,T]}^{\prime}\), and thus

$$ \rho_{t}(\xi)=-E_{\mathbb{Q}^{{q\ast,\xi}}}\bigg[ \xi +\int_{t}^{T}{\hat{G}}(V_{s},Z_{s},q_{s}^{\ast,\xi})ds\bigg\vert \mathcal{F}_{t}\bigg] . $$

In the above representation formula, the convex dual \(\hat{G}\) yields the “penalty” process \({\hat{G}}(V_{s},Z_{s},\cdot)\), \(s\in[0,T]\), which is added to the original risk position. However, it is per se common for all claims and independent of all maturities.

From the representation (3.11) and the properties of \(\hat {G}\), we have the following result.

Corollary 3.6

Consider an arbitrary risk position\(\xi\in\mathcal{L}\)with maturity\(T\). Suppose that Assumptions 2.1and 2.2hold. Then for\(t\in[ 0,T] \), the following properties hold:

(i) (Anti-positivity) \(\rho_{t}( \xi) \leq0\)for\(\xi\geq0 \).

(ii) (Convexity) For any\(\bar{\xi}\in\mathcal{L}^{\infty }(\mathcal{F}_{T})\)and\(\alpha\in\mathcal{L}^{\infty}(\mathcal{F}_{t}) \)with\(\alpha\in[0,1] \), we have\(\rho_{t}( \alpha\xi+(1-\alpha ) \bar{\xi})\leq\alpha\rho_{t}(\xi)+(1-\alpha)\rho_{t}(\bar{\xi}) \).

(iii) (Cash translativity) For any\(m\in\mathcal{L}^{\infty }(\mathcal{F}_{t}) \), we have\(\rho_{t}( \xi -m) =\rho_{t}( \xi) +m\).

It is immediate to see from (3.11) that due to the trading constraints, the replication invariance property in general fails, i.e.,

$$ \rho_{t}\bigg(\xi+\int_{t}^{s}\sum_{i=1}^{n}\frac{\tilde{\pi }^{i}_{u}}{S_{u}^{i}}dS_{u}^{i}\bigg) =\rho_{t}\bigg(\xi+\int_{t}^{s}\pi_{t}^{\mathrm{tr}}\big( \theta (V_{t})dt+dW_{t}\big)\bigg)\neq\rho_{t}(\xi), $$

for \(s\in(t,T]\). This is because \(\mathbb{Q}^{q}\) is not necessarily an equivalent martingale measure, and therefore \(E_{\mathbb{Q}^{q}}[\int_{t}^{s}\pi_{t}^{\mathrm{tr}}( \theta (V_{t})dt+dW_{t})|\mathcal{F}_{t}]\neq0\) in general.

3.3 A parity result between forward and classical entropic risk measures

The third result quantifies the difference between the forward and the classical entropic measures. For a specific investment horizon \([ 0,T] \), we consider the exponential utility at maturity \(T\),

$$ U_{T}(x)=-e^{-\gamma x}, $$

\(x\in\mathbb{R}\), \(\gamma>0\). For the reader’s convenience, we recall the definition of classical entropic risk measures associated with this horizon and utility (see among others [2, 8, 13,14,15,16, 24, 25]).

Definition 3.7

Let \(T>0\) be fixed, and consider a risk position \(\xi\) maturing at \(T\), with \(\xi\in \mathcal{F}_{T}\). Its classical entropic risk measure, denoted by \(\rho_{t,T}(\xi)\in\mathcal{F}_{t}\), is defined for \(t\in[ 0,T] \) via

$$ w^{0}(x,t)=w^{\xi}\big(x+\rho_{t,T}(\xi),t\big), $$

for all \(( x,t) \in\mathbb{R}\times[0,T]\), where

$$ w^{\xi}(x,t):=\mathop{\mathrm{ess}\,\mathrm{sup}}_{\pi\in\mathcal{A}_{[t,T]}}E_{\mathbb{P}} \bigg[ U_{T}\bigg(x+\int_{t}^{T}\pi_{u}^{\mathrm{tr}}\big( \theta (V_{u})du+dW_{u}\big) +\xi\bigg)\bigg\vert \mathcal{F}_{t}\bigg] . $$
(3.12)

The decomposition formula below shows that the forward entropic measure can be constructed as the difference of two classical entropic measures applied, respectively, to the modified risk position \(\xi-\frac{Y_{T}-\lambda T}{\gamma} \) and to a normalizing factor \(-\frac{Y_{T}-\lambda T}{\gamma}\).

Proposition 3.8

Consider an arbitrary risk position\(\xi\in \mathcal{L}\)with maturity\(T\). Suppose that Assumptions 2.1and 2.2hold. Then for\(t\in[ 0,T] \), the forward and classical entropic risk measures satisfy

$$ \rho_{t}(\xi)=\rho_{t,T}\left(\xi-\frac{Y_{T}-\lambda T}{\gamma }\right)-\rho _{t,T}\left(-\frac{Y_{T}-\lambda T}{\gamma}\right), $$
(3.13)

where\(( Y,\lambda) \)is the unique Markovian solution to the ergodic BSDE (2.8) (cf. Proposition 2.5).

3.4 Risk positions with long maturity

We examine the behavior of the forward entropic risk measure and the hedging strategy of risk positions with long maturity. For tractability, we focus on European-type positions written on the stochastic factor process \(V\), namely, we consider risk positions with arbitrary maturity \(T\) of the form

$$ \xi=-g ( V_{T}) . $$
(3.14)

Assumption 3.9

The function \(g:{\mathbb{R}^{d}}\rightarrow {\mathbb{R}}\) is uniformly bounded and Lipschitz-continuous, with Lipschitz constant \(C_{g}\).

We are interested in the behavior of \(\rho_{t}({\xi})\) and its associated hedging strategy \(\alpha_{t,T}\) if \(T\) is large. We first recall from part (ii) of Theorem 3.2 that the forward entropic risk measure is represented as \(\rho_{t}( \xi ) =Y_{t}^{-\xi}\), \(t\in[ 0,T] \), where \(Y_{t}^{-\xi}\) solves the BSDE (3.4). Under the above Markovian assumption (3.14), we further deduce that the solution \(( Y_{t}^{-\xi},Z_{t}^{-\xi}) \) of (3.4) can be actually represented in the form

$$ (Y_{t}^{-\xi},Z_{t}^{-\xi})=\big(y^{T,g}(V_{t},t),z^{T,g}(V_{t},t)\big), $$

for some measurable functions \(y^{T,g}(\cdot,\cdot),z^{T,g}(\cdot,\cdot)\), and in turn,

$$ \rho_{t} ( \xi) =y^{T,g}(V_{t},t), $$
(3.15)

where \(V\) solves (2.1) with \(V_{0}=v\). Therefore, taking (without loss of generality) \(t=0\), we study the limit \(\lim_{T\uparrow\infty }\rho _{0}( \xi) =\lim_{T\uparrow\infty}y^{T,g}(v,0)\).

We establish that as \(T\uparrow\infty\), \(\rho_{0}( \xi ) \) converges to a constant which is independent of the initial value of the stochastic factor and moreover, we prove the rate of convergence. We also study the limiting behavior of the hedging strategies and establish appropriate exponential bounds. These yield that as \(T\uparrow\infty\), the optimal strategies with and without the risk position coincide, and thus at all times, no additional stock trading to hedge the risk position takes place.

Theorem 3.10

Consider an arbitrary risk position\(\xi \)as in (3.14) with maturity\(T\), and the function\(y^{T,g}( \cdot,\cdot) \)as in (3.15). Suppose that Assumptions 2.1, 2.2and 3.9hold. Then the following assertions hold:

(i) For any\(v\in\mathbb{R}^{d}\)and\(V_{0}=v\), there exists a constant\(L^{g}\in\mathbb{R}\), independent of\(v\), such that

$$ \lim_{T\uparrow\infty}\rho_{0}({\xi})=\lim_{T\uparrow\infty }y^{T,g}(v,0)=L^{g}. $$

In particular, for any\(T>0\),

$$ |y^{T,g}(v,0)-L^{g}|\leq C(1+|v|^{2})e^{-\hat{C}_{\eta}T} $$
(3.16)

for some constant\(C\), where the constant\(\hat{C}_{\eta}\)is given in Proposition 2.3.

(ii) The hedging strategy satisfies for any\(T>0\)and\(s\in [0,T)\)that

$$ E_{\mathbb{P}}\left[ \int_{0}^{s}|\alpha_{t,T}|^{2}dt\right] \leq C (1+|v|^{4}) e^{-2\hat{C}_{\eta}(T-s)}. $$
(3.17)

Therefore, for any\(s\geq0\),

$$ \lim_{T\uparrow\infty}E_{\mathbb{P}}\left[ \int_{0}^{s}|\alpha _{t,T}|^{2}dt\right] =0. $$
(3.18)

Remark 3.11

In order to study the long-maturity behavior of the solution \(Y_{0}^{-\xi}\) to the BSDE (3.4), it is natural to try to relate (3.4) with an ergodic BSDE, given below, and investigate the proximity of their solutions. Specifically, we may consider the ergodic BSDE

$$ {P}_{t}={P}_{s}+\int_{t}^{s}\big( G(V_{u},Z_{u},{Q}_{u})-\hat{\lambda} \big) ds-\int_{t}^{s}{Q}_{u}^{\mathrm{tr}}dW_{u}, $$
(3.19)

for \(0\leq t\leq s<\infty\), and examine the approximation of \(Y_{0}^{-\xi }\) by \(P_{0}+\hat{\lambda}T\) for large \(T\).

However, the driver of the ergodic BSDE (3.19) depends on the solution \(Z\) of the ergodic BSDE (2.8) of the forward performance process, and this causes various technical issues. Indeed, the driver \(G(v,z(v),\bar{z})\) of the ergodic BSDE (3.19) depends on the function \(z(\cdot)\) in (2.10). Although, due to the boundedness of the function \(z(\cdot)\), the driver \(G\) satisfies the local Lipschitz estimate (5.2) in \(\bar{z}\), it need not satisfy the local Lipschitz estimate (5.1) in \(v\), and hence the existence and uniqueness result in [23] might not apply. Moreover, it is not even clear whether the ergodic BSDE (3.19) is well-posed. For these reasons, we establish the above results working directly with the function \(y^{T,g}(\cdot,\cdot)\) in (3.15).

4 An example

We present an example for which we derive explicit formulae for both the forward and classical entropic risk measures, and also provide numerical results for their large-maturity limits.

The market consists of a bond and a stock. The stock’s coefficients depend on a single stochastic factor driven by a 2-dimensional Brownian motion, namely,

$$\begin{aligned} dS_{t}&=b ( V_{t}) S_{t}dt+\sigma( V_{t}) S_{t}dW_{t}^{1},\\ dV_{t}&=\eta( V_{t}) dt+\kappa_{1}dW_{t}^{1}+\kappa _{2}dW_{t}^{2}, \end{aligned}$$

for some positive constants \(\kappa_{1},\kappa_{2}\). We assume that \(|\kappa_{1}|^{2}+|\kappa_{2}|^{2}=1\), the functions \(b(\cdot)\) and \(\sigma(\cdot)\) are uniformly bounded with \(\sigma(\cdot)>0\), and \(\eta(\cdot)\) satisfies the dissipativity condition (2.3) in Assumption 2.2. We choose the set of constraints \(\Pi \equiv \mathbb{R} \times\{0\}\) (so that \(\pi_{1,t}=\tilde{\pi}_{t}\sigma(V_{t})\in\mathbb{R}\) and \(\pi_{2,t}\equiv0\)). Therefore, the wealth equation (2.6) becomes

$$ dX_{t}^{\pi_{1}}=\pi_{1,t}\big( \theta(V_{t})dt+dW_{t}^{1}\big) , $$

with \(\theta( V_{t}) =\frac{b( V_{t}) }{\sigma ( V_{t}) }\). We consider a risk position as in (3.14), \(\xi=-g( V_{T}) \), for some function \(g(\cdot)\) satisfying Assumption 3.9.

4.1 Forward entropic risk measure

The drivers \(F\) and \(G\) in (2.9) and (3.5) take the forms

$$\begin{aligned} F\big( v,(z_{1},z_{2})^{\mathrm{tr}}\big) &=-\theta( v) z_{1}-\frac{1}{2 }|\theta( v) |^{2}+\frac{1}{2}|z_{2}|^{2},\\ G\left( v,(z_{1},z_{2})^{\mathrm{tr}},(\bar{z}_{1},\bar{z}_{2})^{\mathrm{tr}}\right)& =-\theta \left( v\right) \bar{z}_{1}+z_{2}\bar{z}_{2}+\frac{\gamma}{2}|\bar{z} _{2}|^{2}, \end{aligned}$$

for \(z=(z_{1},z_{2})^{\mathrm{tr}}\in\mathbb{R}^{2}\) and \(\bar{z}=(\bar {z}_{1},\bar{z }_{2})^{\mathrm{tr}}\in\mathbb{R}^{2}\). The convex dual of \(G\) (cf. (3.7)) is then given, for \(v\in\mathbb{R},z=(z_{1},z_{2})^{\mathrm{tr}}\in\mathbb {R}^{2}\) and \(p=(p_{1},p_{2})^{\mathrm{tr}}\in\mathbb{R}^{2}\), by

$$ \hat{G}\left( v,(z_{1},z_{2})^{\mathrm{tr}},(p_{1},p_{2})^{\mathrm{tr}}\right) =\frac{ |p_{2}-z_{2}|^{2}}{2\gamma}\boldsymbol{1}_{\{p_{1}+\theta(v)=0\} }+\infty \mathbf{1}_{\{p_{1}+\theta(v)\neq0\}}. $$
(4.1)

To solve the BSDE (3.4), we first introduce the auxiliary quadratic BSDE

$$\begin{aligned} dY_{t}^{-\xi} =&-\left( \left( -\kappa_{1}\theta( V_{t}) +\kappa_{2}Z_{2,t}\right) Z_{t}^{-{\xi}}+\frac{\gamma|\kappa_{2}|^{2}}{ 2}|Z_{t}^{-{\xi}}|^{2}\right) dt \\ &+Z_{t}^{-\xi}( \kappa_{1}dW_{t}^{1}+\kappa_{2}dW_{t}^{2}) \end{aligned}$$
(4.2)

with \(Y_{T}^{-\xi}=-\xi=g( V_{T}) \), and show that it admits a unique solution, say \((Y^{-\xi},Z^{-\xi})\). It then follows that the processes \({(Y^{-\xi},(Z_{1}^{-\xi},Z_{2}^{-\xi})^{\mathrm{tr}})}\), with \(Z_{1,t}^{-\xi}:=\kappa_{1}Z_{t}^{-\xi}\) and \(Z_{2,t}^{-\xi}:=\kappa _{2}Z_{t}^{-\xi}\), solve (uniquely) the original BSDE (3.4). To solve (4.2), we define

$$ \tilde{Y}_{t}^{-\xi}=e^{\gamma|\kappa_{2}|^{2}Y_{t}^{-\xi}}\quad \text{and}\quad\tilde{Z}_{t}^{-\xi}=\gamma|\kappa_{2}|^{2}\tilde{Y} _{t}^{-{\xi}}Z_{t}^{-\xi}, $$
(4.3)

and deduce from (4.2) that they satisfy

$$ d\tilde{Y}_{t}^{-{\xi}}=\tilde{Z}_{t}^{-{\xi}}\left( \left( \kappa _{1}\theta( V_{t}) -\kappa_{2}Z_{2,t}\right) dt+\kappa _{1}dW_{t}^{1}+\kappa_{2}dW_{t}^{2}\right) $$

with \(\tilde{Y}_{T}^{-{\xi}}=e^{\gamma|\kappa_{2}|^{2}g( V_{T}) }\). Because \(\theta(\cdot)\) and \(Z_{2}\) are uniformly bounded, the process \(B_{t}:=\int_{0}^{t}( \kappa_{1}\theta ( V_{s}) -\kappa_{2}Z_{2,s}) ds+\kappa_{1}W_{t}^{1}+\kappa_{2}W_{t}^{2}\), \(t \in[0,T]\), is a Brownian motion under the probability measure ℚ defined by

$$ \left. \frac{d\mathbb{Q}}{d\mathbb{P}}\right\vert_{\mathcal{F}_{T}}= \mathcal{E}\bigg( -\int_{0}^{\cdot}\big( \kappa_{1}\theta( V_{s}) -\kappa_{2}Z_{2,s}\big) (\kappa _{1}dW_{s}^{1}+\kappa_{2}dW_{s}^{2})\bigg) _{T}\text{.} $$
(4.4)

Hence, \(d\tilde{Y}_{t}^{-\xi}= \tilde{Z}_{t}^{-\xi}dB_{t}\) and thus \(\tilde{Y}_{t}^{-\xi}=E_{\mathbb{Q}} [ e^{\gamma|\kappa_{2}|^{2}g( V_{T}) }|\mathcal{F}_{t} ] \). We then readily deduce, using (4.3) and (3.6), the closed-form expression

$$ \rho_{t}(\xi)=Y_{t}^{-\xi}=\frac{1}{\gamma|\kappa_{2}|^{2}}\ln E_{ \mathbb{Q}}[ e^{\gamma|\kappa_{2}|^{2}g( V_{T}) }\vert\mathcal{ F}_{t}] . $$
(4.5)

For the convex dual representation, (3.11) gives

$$ \rho_{t}(\xi)=-\mathop{\mathrm{ess}\,\mathrm{inf}}_{q\in\mathcal{A}_{[t,T]}^{\prime}}E_{ \mathbb{Q}^{q}}\left[ \left. -g( V_{T}) +\int_{t}^{T}{\hat{G}} \big(V_{s},(Z_{1,s},Z_{2,s})^{\mathrm{tr}},(q_{1,s},q_{2,s})^{\mathrm{tr}}\big)ds\right \vert\mathcal{F }_{t}\right] , $$

for \(q=( q_{1},q_{2}){^{\mathrm{tr}}} \) and \(\mathcal{A}_{[t,T]}^{\prime}\) as in (3.10). It is clear from (4.1) that the optimal density process must satisfy \(q_{1,s}=-\theta(V_{s})\), \(s\in[ 0,T] \), and thus

$$ \rho_{t}(\xi)=-\mathop{\mathrm{ess}\,\mathrm{inf}}_{q\in\mathcal{A}_{[t,T]}^{\prime },\, q_{1}=-\theta( V) }E_{\mathbb{Q}^{q}}\left[ \left. -g\left( V_{T}\right) +\frac{1}{2\gamma}\int_{t}^{T} \vert q_{2,s}-Z_{2,s} \vert^{2}ds\right\vert \mathcal{F}_{t}\right] . $$

Furthermore, under \(\mathbb{Q}^{q}\), the stock price process \(S\) follows

$$ dS_{t}=\sigma(V_{t})S_{t}dW_{t}^{{q},1}, $$

where \(W^{{q},1}=W^{1}+\int_{0}^{\cdot}\theta(V_{s})ds\) is a Brownian motion under \(\mathbb{Q}^{q}\). Therefore, \(\mathbb{Q}^{q}\) is an equivalent martingale measure.

Note that in such a case without portfolio constraints, the above convex dual representation implies that the forward entropic risk measure indeed satisfies the replication invariance property, namely,

$$ \rho_{t}\left(\xi+\int_{t}^{s}\frac{\tilde{\pi}_{u}}{S_{u}}dS_{u}\right)=\rho _{t}\left(\xi+\int_{t}^{s}\pi_{u}^{1}dW_{u}^{q,1}\right)=\rho_{t}(\xi), $$

for any \(s\in[t,T]\), as it follows from the martingale property of \(\int\pi_{u}^{1}dW_{u}^{q,1}\) under the equivalent martingale measure \(\mathbb{Q}^{q}\).

4.2 Classical entropic risk measure

We have the representation

$$ \rho_{t,T}(\xi)=P_{t}^{-\xi}-P_{t}^{0}, $$

where \(P_{t}^{-\xi}\), \(t\in[0,T]\), is the unique solution to the quadratic BSDE

$$\begin{aligned} P_{t}^{-{\xi}} =&-{\xi}+\frac{1}{\gamma}\int_{t}^{T}F( {V_{s}},\gamma Q_{s}^{-{\xi}}) ds-\int_{t}^{T}(Q_{s}^{-{\xi} })^{\mathrm{tr}}dW_{s} \\ =&g(V_{T})+\frac{1}{2\gamma}\int_{t}^{T}\big( \gamma ^{2}|Q_{2,s}^{-\xi}|^{2}-|\theta(V_{s})|^{2}-2{\gamma}\theta (V_{s})Q_{1,s}^{-\xi}\big) ds \\ &-\int_{t}^{T}(Q_{s}^{-\xi })^{\mathrm{tr}}dW_{s}; \end{aligned}$$
(4.6)

see for example [16, Sect. 3]. Direct calculations then yield the closed-form representation

$$ \rho_{t,T}(\xi)=P_{t}^{-\xi}-P_{t}^{0}=\frac{1}{\gamma|\kappa_{2}|^{2}} \ln E_{\mathbb{Q}^{T}}[ e^{\gamma|\kappa_{2}|^{2}g( V_{T}) }\vert\mathcal{F}_{t}] , $$
(4.7)

where the measure \(\mathbb{Q}^{T}\) equivalent to ℙ is defined by

$$ \left. \frac{d\mathbb{Q}^{T}}{d\mathbb{P}}\right\vert_{\mathcal{F}_{T}}= \mathcal{E}\bigg( -\int_{0}^{\cdot}\big( \kappa_{1}\theta( V_{s}) -\kappa_{2}\gamma Q_{2,s}^{0}\big) (\kappa _{1}dW_{s}^{1}+\kappa_{2}dW_{s}^{2})\bigg) _{T}. $$
(4.8)

In this single stock/single factor example, the only difference in the expressions (4.5) and (4.7) for the forward and classical entropic risk measures is in the respective measures ℚ and \(\mathbb{Q}^{T}\) (cf. (4.4) and (4.8)). In the forward case, ℚ is determined by the component \(Z_{2}\) appearing in the ergodic BSDE representation of the forward performance process (2.12). The corresponding density process is naturally independent of the maturity \(T\). In the classical setting, however, the measure \(\mathbb{Q}^{T}\) is determined by the component \(Q_{2}^{0}\) coming from the exponential utility maximization (3.12) with zero risk position (cf. (4.6) with \({\xi}=0\)), which depends critically on the maturity \(T\). Finally, (4.4) and (4.8) yield

$$\begin{aligned} \frac{d\mathbb{Q}^{T}}{d\mathbb{Q}}\bigg\vert _{\mathcal{F} _{T}} &=e^{\int_{0}^{t}\kappa_{1}\theta(V_{s})\kappa_{2}(\gamma Q_{2,s}^{0}-Z_{2,s})ds} \\ &\phantom{=:} \times\mathcal{E}\bigg( \int_{0}^{\cdot}\kappa_{2}( \gamma Q_{2,s}^{0}-Z_{2,s}) (\kappa_{1}dW_{s}^{1}+\kappa _{2}dW_{s}^{2})\bigg)_{T}. \end{aligned}$$

4.3 Numerical results

We conclude with numerical results for the forward and the classical entropic risk measures, \(\rho_{0}(\xi)\) and \(\rho_{0,T}(\xi)\), respectively, taking \(T\) to be large, with \(\eta(v)=-\alpha v\), \(\theta(v)=(K_{2}-|v|)^{+}\) and \(g(v)=(K_{1}-|v|)^{+}\), with \(K_{1}{, K_{2}}>0\). Thus, the stochastic factor process follows the Vasiček model

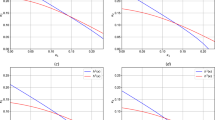
$$ dV_{t}=-\alpha V_{t}dt+\kappa_{1}dW_{t}^{1}+\kappa_{2}dW_{t}^{2}, $$

and the risk position is \(\xi=-(K_{1}-|V_{T}|)^{+}\). Figures 1–3 provide the values of both the forward and classical entropic risk measures, with different starting points of \(V_{0}\) and different values of \((\kappa_{1},\kappa_{2})\). The graphs confirm the large-maturity behavior of both measures as well as that the limiting constants are indeed independent of the initial value \(V_{0}\) of the stochastic factor process.

Fig. 1
figure 1

Forward and classical entropic risk measures against the maturity \(T \), with \(\gamma=1 \), \(\alpha=0.1 \), \(K_{1}=K_{2}=10 \), \(\kappa_{1}=0.9 \), \(\kappa_{2}=0.1 \); blue upward-pointing triangle for \(v_{0}=5 \), red circle for \(v_{0}=7.5 \), green asterisk for \(v_{0}=10 \), black cross for \(v_{0}=12.5 \), and magenta square for \(v_{0}=15 \)

Full size image

Note that \(\kappa_{1}\) is the correlation between the stochastic factor \(V\) and the stock \(S\). The larger \(\kappa_{1}\), the more likely the investor is able to hedge the underlying risks via trading the stock. The numerical results in Figs. 1 and 3 show that in both extreme cases, \(\kappa_{1}\approx1\) or \(\kappa_{1}\approx0\), both the forward and classical entropic risk measures converge to constants more quickly, in comparison to the intermediate case \(\kappa=0.5\). This implies that in these two extreme situations, the investor will implement earlier the “no trading in the stock” strategy.

On the other hand, Fig. 2 illustrates that when \(\kappa _{2}=0.5\), in which case the stock can be used to partially hedge the underlying risks, the forward entropic risk measure will converge to a constant faster than its classical counterpart. As a consequence, if the investor chooses to use the forward entropic risk measure to assess the risk position, she will implement the “no-trading in the stock” strategy earlier.

Fig. 2
figure 2

Forward and classical entropic risk measures against the maturity \(T \), with \(\gamma=1 \), \(\alpha=0.1 \), \(K_{1}=K_{2}=10 \), \(\kappa_{1}=0.5 \), \(\kappa_{2}=0.5 \); blue upward-pointing triangle for \(v_{0}=5 \), red circle for \(v_{0}=7.5 \), green asterisk for \(v_{0}=10 \), black cross for \(v_{0}=12.5 \), and magenta square for \(v_{0}=15 \)

Full size image
Fig. 3
figure 3

Forward and classical entropic risk measures against the maturity \(T \), with \(\gamma=1 \), \(\alpha=0.1 \), \(K_{1}=K_{2}=10 \), \(\kappa_{1}=0.0 \), \(\kappa_{2}=1.0 \); blue upward-pointing triangle for \(v_{0}=5 \), red circle for \(v_{0}=7.5 \), green asterisk for \(v_{0}=10 \), black cross for \(v_{0}=12.5 \), and magenta square for \(v_{0}=15 \)

Full size image

We should, however, like to mention that it is not yet clear how the two limiting constants compare to each other. This open question is left for future research.

5 Proofs of the main results

5.1 Proof of Theorem 3.2

We recall that in the proof of [23, Proposition 4.1], two key inequalities were used, which follow from Assumption 2.1 and the Lipschitz property of the distance function. Specifically, it was established that there exist constants \(C_{v},C_{z}>0\) such that for any \(v,v_{1},{v} _{2},z,z_{1},{z}_{2}\in\mathbb{R}^{d}\), the driver \(F\) in (2.9) satisfies

$$\begin{aligned} |F(v_{1},z)-F({v}_{2},z)|&\leq C_{v}(1+|z|)|v_{1}-{v}_{2}|, \end{aligned}$$
(5.1)
$$\begin{aligned} |F(v,z_{1})-F(v,{z}_{2})|&\leq C_{z}(1+|z_{1}|+|{z}_{2}|)|z_{1}-{z}_{2}|. \end{aligned}$$
(5.2)

Proof of (i)

First note that for \(t\in[ 0,T] \), \(G(v,Z_{t},\bar{z})\) is locally Lipschitz-continuous in \(\bar{z}\), since

$$ |G(v,Z_{t},\bar{z}_{1})-G(v,Z_{t},\bar{z}_{2})|\leq C_{z}(1+2|Z_{t}|+\gamma| \bar{z}_{1}|+\gamma|\bar{z}_{2}|)|\bar{z}_{1}-\bar{z}_{2}|\quad\text{a.s.} $$

and \(Z\) is uniformly bounded. Using in addition that \({\xi}\in \mathcal{L}^{\infty}( \mathcal{F}_{T}) \), the assertion follows from [22, Theorems 2.3 and 2.6] and [16, Theorem 7]. □

Proof of (ii)

As mentioned in the discussions before Sect. 3.1, it might not be possible to solve (3.2) within the standard framework of exponential utility maximization because the modified risk position \(\xi -\frac{Y_{T}-\lambda T}{\gamma}\) is possibly neither bounded nor exponentially integrable. Instead, we provide an alternative approach, claiming directly that its solution \(u^{\xi}(x,t)\) admits the representation

$$ {u}^{\xi}(x,t)=U(x,t)e^{\gamma Y_{t}^{-\xi}}, $$
(5.3)

with \(U(x,t)\) as in (2.12) and \(Y_{t}^{-\xi}\) solving (3.4).

If (5.3) holds, we deduce from (2.12) that for \(t\in[ 0,T] \),

$$ {u}^{\xi}\big(x+\rho_{t}(\xi),t\big)=U\big(x+\rho_{t}(\xi),t\big)e^{\gamma Y_{t}^{-\xi }}=U(x,t)e^{-\gamma\rho_{t}(\xi)}e^{\gamma Y_{t}^{-\xi}}, $$

and in turn, the representation (3.6) follows directly from (3.1).

To verify (5.3), it suffices to establish that the process \(U(X_{s}^{t,x;\pi},s)e^{\gamma Y_{s}^{-\xi}}\) for \(s\in[ t,T]\) is a supermartingale for any \(x\in\mathbb{R}\) and \(\pi\in\mathcal{A}_{[t,T]}\), and that there exists an optimal \(\pi^{\ast}\in\mathcal{A}_{[t,T]}\) such that \(U(X_{s}^{t,x;\pi ^{\ast}},s)e^{\gamma Y_{s}^{-\xi}}\) becomes a martingale, where

$$ X_{s}^{t,x;\pi}:=x+\int_{t}^{s}\pi_{u}^{\mathrm{tr}}\big(\theta (V_{u})du+dW_{u}\big) $$
(5.4)

and analogously for \(X^{t,x;\pi^{\ast}}\). Indeed, using (5.4) together with (2.12), (2.8) and (3.4), we deduce that for \(s\in[ t,T]\),

$$ U(X_{s}^{t,x;\pi},s)e^{\gamma Y_{s}^{-\xi}}= -e^{-\gamma X_{s}^{t,x;\pi }}e^{Y_{s}-\lambda s}e^{\gamma Y_{s}^{-\xi}}=U(x,t)e^{\gamma Y_{t}^{-\xi }}A_{t,s}^{\pi}, $$

with

$$ A_{t,s}^{\pi}:=e^{\int_{t}^{s}(Z_{u}+\gamma Z_{u}^{-\xi }-\gamma\pi_{u})^{\mathrm{tr}}dW_{u}-{\int_{t}^{s}}(\gamma\pi _{u}^{\mathrm{tr}}\theta(V_{u})+F(V_{u},Z_{u}+\gamma Z_{u}^{-\xi}))du}. $$

Following arguments similar to those in the proof of [23, Theorem 3.2], we obtain that for \(s\in[ t,T] \) and any \(\pi\in\mathcal{A}_{[t,T]}\), we have \(E_{\mathbb{P}}[ A_{t,s}^{\pi}\vert\mathcal{F}_{t}] \geq1\), while we obtain \(E_{\mathbb{P}}[ A_{t,s}^{\pi^{\ast}}\vert\mathcal{F}_{t} ] =1\) for

$$ \pi_{s}^{\ast,\xi}=\mathrm{Proj}_{\Pi}\left( Z_{s}^{-{\xi}}+ \frac{\theta(V_{s})+Z_{s}}{\gamma}\right) . $$
(5.5)

Hence, we obtain that

$$ E_{\mathbb{P}}[ U(X_{T}^{t,x;\pi}+\xi,T) \vert \mathcal{F}_{t}]=E_{\mathbb{P}}[U(X_{T}^{t,x;\pi},T)e^{\gamma Y_{T}^{-\xi}}\vert\mathcal{F}_{t}]\leq U(x,t)e^{\gamma Y_{t}^{-\xi}}\! = u^{\xi}(x,t) $$

for any \(\pi\in\mathcal{A}_{[t,T]}\), where we also used that \(Y_{T}^{-\xi}=-\xi\) (cf. (3.4)). Similarly, with \(\pi ^{\ast}\) as in (5.5), we obtain that

$$ E_{\mathbb{P}}[ U(X_{T}^{t,x;\pi^{\ast}}+\xi,T) \vert \mathcal{F}_{t}] =u^{\xi}(x,t), $$

and (5.3) follows. □

5.2 Proof of Theorem 3.5

We first derive some auxiliary bounds for the driver \(G\) and its convex dual \(\hat{G}\).

Lemma 5.1

The driver\(G(v,z,\bar{z})\)and its convex dual\({\hat{G}}(v,z,p)\) (cf. (3.5) and (3.7), respectively) have the following properties:

(i) For\((v,z,\bar{z})\in\mathbb{R}^{d}\times\mathbb {R}^{d}\times\mathbb{R} ^{d}\),

$$ -\gamma|\bar{z}|^{2}-\frac{2}{\gamma}(|\theta(v)|^{2}+|z|^{2})\leq G(v,z, \bar{z})\leq\gamma|\bar{z}|^{2}+\frac{2}{\gamma}(|\theta (v)|^{2}+|z|^{2}). $$
(5.6)

(ii) For\((v,z)\in\mathbb{R}^{d}\times\mathbb{R}^{d}\), \({\hat{G}} (v,z,p)\)is convex in\(p\).

(iii) For\((v,z,p)\in\mathbb{R}^{d}\times\mathbb{R}^{d}\times \mathbb{R} ^{d}\),

$$ {\hat{G}}(v,z,p)\geq\max\left( 0,\frac{|p|^{2}}{4\gamma}-\frac {2}{\gamma} (|\theta(v)|^{2}+|z|^{2})\right) . $$
(5.7)

Proof

The convexity of \(\hat{G}(v,z,p)\) in \(p\) is immediate, so we only prove (i) and (iii).

Since \(0\in\Pi\), we have that \(\mathrm{dist}^{2}( \Pi,\frac{\theta(v)+z}{ \gamma}) \leq\frac{|\theta(v)+z|^{2}}{\gamma^{2}}\) and thus \(F(v,z)\leq\frac{1}{2}|z|^{2}\). On the other hand, \(F(v,z)\geq-z^{\mathrm{tr} }\theta (v)-\frac{1}{2}|\theta(v)|^{2}\). Therefore, (3.5) gives

$$\begin{aligned} G(v,{z},\bar{z}) =&\frac{1}{\gamma}\big( F(v,{z}+\gamma\bar{z})-F(v,{z} )\big) \\ \leq& \frac{1}{2\gamma}|z+\gamma\bar{z}|^{2}+\frac{1}{\gamma}\bigg(z^{\mathrm{tr}}\theta (v)+\frac{1}{2}|\theta(v)|^{2}\bigg) \\ \leq&\gamma|\bar{z}|^{2}+\frac{2}{\gamma}\big(|z|^{2}+|\theta(v)|^{2}\big). \end{aligned}$$

In turn, using the definition (3.7) of \(\hat{G}\) and the above inequality, we deduce that for any \(\bar{z}\in\mathbb{R}^{d}\),

$$ {\hat{G}}(v,z,p)\geq\bar{z}^{\mathrm{tr}}p-G(v,z,\bar{z})\geq\bar{z}^{\mathrm{tr} }p-\gamma| \bar{z}|^{2}-\frac{2}{\gamma}\big(|\theta(v)|^{2}+\left\vert z\right \vert ^{2}\big). $$

Taking \(\bar{z}=p/2\gamma\) yields

$$ {\hat{G}}(v,z,p)\geq\frac{|p|^{2}}{4\gamma}-\frac{2}{\gamma}\big(|z|^{2}+|\theta(v)|^{2}\big). $$

Moreover, since \(G(v,z,0)=0\), we have by taking \(\bar{z}=0\) that \(\hat{G}(v,z,p)\geq 0\), and we conclude. The lower bound in (5.6) is derived by using similar arguments. □

Proof of Theorem 3.5

(i) Let \(T>0\) be the maturity of the arbitrary risk position \(\xi\). For any \(q\in\mathcal{A}_{[0,T]}^{\prime}\) and with \(\mathbb{Q}^{q}\) defined via \(\frac{d\mathbb{Q}^{q}}{d \mathbb{P}}|_{\mathcal{F}_{T}}=\mathcal{E}( \int_{0}^{.}q_{s}^{\mathrm{tr}}dW_{s})_{T}\), let

$$ Y_{t}^{-\xi,q}:=E_{\mathbb{Q}^{q}}\left[ \left. -\xi-\int_{t}^{T}{\hat{G}} (V_{s},Z_{s},q_{s})ds\right\vert\mathcal{F}_{t}\right] $$

for \(t\in[ 0,T]\). Then \(Y_{t}^{-\xi,q}\) is finite due to the integrability condition on \(\hat{G}\) in the admissible set \(\mathcal{A}_{[0,T]}^{\prime}\).

Next, observe that the process \(Y_{t}^{-\xi,q}-\int_{0}^{t}\hat{G} (V_{s},Z_{s},q_{s})ds\), \(t\in[0,T]\), is a uniformly integrable martingale under \(\mathbb{Q}^{q}\). Thus, the martingale representation theorem (see for example [20, Chap. 5.8]) gives

$$\begin{aligned} Y_{t}^{-\xi,q}-\int_{0}^{t}\hat{G}(V_{s},Z_{s},q_{s})ds&=\left( -\xi -\int_{0}^{T}{\hat{G}}(V_{s},Z_{s},q_{s})ds\right) \\ &\phantom{=:}-\int_{t}^{T}(Z_{s}^{-\xi ,q})^{\mathrm{tr}}dW_{s}^{q} \end{aligned}$$
(5.8)

for some predictable process \(Z^{-\xi,q}\), where \(W_{t}^{q}=W_{t}-\int_{0}^{t}q_{s}ds\), \(t\in[0,T]\), is a \(d\)-dimensional Brownian motion under \(\mathbb{Q}^{q}\). On the other hand, the BSDE (3.4) takes under \(\mathbb{Q}^{q}\) the form

$$ Y_{t}^{-\xi}=-\xi+\int_{t}^{T}\left( G(V_{s},Z_{s},Z_{s}^{-\xi })-(Z_{s}^{-\xi})^{\mathrm{tr}}q_{s}\right) ds-\int_{t}^{T}(Z_{s}^{-\xi })^{\mathrm{tr}}dW_{s}^{q}. $$
(5.9)

Combining (5.8) and (5.9) gives

$$ Y_{t}^{-\xi}-Y_{t}^{-\xi,q}=E_{\mathbb{Q}^{q}}\bigg[ \int_{t}^{T}\big( G(V_{s},Z_{s},Z_{s}^{-\xi})-(Z_{s}^{-\xi})^{\mathrm{tr}}q_{s}+{ \hat{G}}(V_{s},Z_{s},q_{s})\big) ds\bigg\vert \mathcal{F}_{t}\bigg] . $$

Using (3.8), we deduce that for any \(q\in\mathcal{A} _{[0,T]}^{\prime}\),

$$ G(V_{s},Z_{s},Z_{s}^{-\xi})-(Z_{s}^{-\xi})^{\mathrm{tr}}q_{s}+{\hat{G}} (V_{s},Z_{s},q_{s})\geq0, $$

and thus \(Y_{t}^{-\xi}\geq Y_{t}^{-\xi,q}\). Next, setting \(q_{s}^{\ast,\xi}:=\partial G_{\bar{z}}(V_{s},Z_{s},Z_{s}^{- {\xi}})\), we further obtain from (3.9) that

$$ G(V_{s},Z_{s},Z_{s}^{-\xi})-(Z_{s}^{-\xi})^{\mathrm{tr}}q_{s}^{\ast,\xi }+{\hat{G}} (V_{s},Z_{s},q_{s}^{\ast,\xi})=0, $$
(5.10)

from which we conclude that \(Y_{t}^{-\xi}=Y_{t}^{-\xi,q^{\ast}}\) for \(t\in[0,T]\).

(ii) We now show that for \(s\in[0,T]\), \(q_{s}^{\ast,\xi}\) is indeed in the admissible set \(\mathcal{A}_{[0,T]}^{\prime}\). To this end, using the lower bound of \(\hat{G }\) in (5.7), we deduce from (5.10) that

$$\begin{aligned} G(V_{s},Z_{s},Z_{s}^{-\xi}) =&(Z_{s}^{-\xi})^{\mathrm{tr}}q_{s}^{\ast,\xi }-{\hat{G}}(V_{s},Z_{s},q_{s}^{\ast,\xi})\\ \leq& (Z_{s}^{-\xi})^{\mathrm{tr}}q_{s}^{\ast,\xi}-\frac{|q_{s}^{\ast,\xi }|^{2}}{4\gamma}+\frac{2}{\gamma}\big(|\theta (V_{s})|^{2}+|Z_{s}|^{2}\big)\\ \leq& 2\gamma|Z_{s}^{-\xi }|^{2}+\frac{|q_{s}^{\ast,\xi}|^{2}}{8\gamma }-\frac{|q_{s}^{\ast,\xi}|^{2}}{4\gamma}+\frac{2}{\gamma }\big(|\theta(V_{s})|^{2}+|Z_{s}|^{2}\big), \end{aligned}$$

where the last inequality used that \(ab\leq2\gamma|a|^{2}+\frac{ |b|^{2}}{8\gamma}\). Combining the above inequality and the lower bound of \(G \) in (5.6) gives

$$\begin{aligned} \frac{1}{8\gamma}|q_{s}^{\ast,\xi}|^{2} \leq&2\gamma|Z_{s}^{-\xi}|^{2}+ \frac{2}{\gamma}\big(|\theta (V_{s})|^{2}+|Z_{s}|^{2}\big)-G(V_{s},Z_{s},Z_{s}^{-\xi}) \\ \leq&3\gamma|Z_{s}^{-\xi}|^{2}+\frac{4}{\gamma}\big(|\theta (V_{s})|^{2}+|Z_{s}|^{2}\big). \end{aligned}$$

Furthermore, since \(Z^{-\xi}\in\mathcal{L}_{\mathrm{BMO}}^{2}[0,T]\) and both \(Z\) and \(\theta(\cdot)\) are bounded, we obtain that \(q^{\ast,\xi}\in \mathcal{L} _{\mathrm{BMO}}^{2}[0,T]\). Finally, using (5.10) and the bounds of \(G\) in (5.6), we deduce that

$$\begin{aligned} &E_{\mathbb{Q}^{q^{\ast,\xi}}}\left[ \int_{0}^{T}|{\hat{G}}(V_{s},Z_{s},q_{s}^{ \ast,\xi})|ds\right]\\ &=E_{\mathbb{Q}^{q^{*,\xi}}}\left[\int_{0}^{T}|(Z_{s}^{-\xi})^{\mathrm{tr}}q_{s}^{*,\xi }-G(V_{s},Z_{s},Z_{s}^{-\xi})|ds\right]\\ &\leq\bigg(\frac{1}{2}+\gamma\bigg)E_{\mathbb{Q}^{q^{\ast,\xi}}}\left[ \int_{0}^{T}|Z_{s}^{-\xi}|^{2}ds\right] +\frac{1}{2}E_{\mathbb{Q}^{q^{\ast,\xi }}}\left[ \int_{0}^{T}|q_{s}^{\ast,\xi}|^{2}ds\right]\\ &\phantom{=:}+\frac{2}{\gamma}E_{\mathbb{Q}^{q^{\ast,\xi}}}\left[ \int_{0}^{T}\big( |\theta(V_{s})|^{2}+|Z_{s}|^{2}\big) ds\right]. \end{aligned}$$

Moreover, since \(Z^{-\xi},q^{\ast,\xi}\in\mathcal{L}_{\mathrm{BMO} }^{2}[0,T]\) under ℙ and \(\mathbb{P}\sim\mathbb{Q}^{q^{\ast,\xi}}\) and moreover, the density process for \(\mathbb{Q}^{q^{*,\xi}}\) is \(\mathcal{E}(\int_{0}^{\cdot}(q^{*,\xi}_{s})^{\mathrm{tr}}dW_{s})\) with \(q^{*,\xi}\in\mathcal{L}_{\mathrm{BMO}}^{2}[0,T]\), we deduce that \(Z^{-\xi}\), \(q^{\ast,\xi}\in\mathcal{L}_{\mathrm{BMO}}^{2}[0,T]\) under \(\mathbb{Q} ^{q^{\ast,\xi}}\) as well (see for example [17, Sect. 5.2]). Thus \(E_{\mathbb{Q}^{q^{\ast,\xi}}}[\int_{0}^{T}|G^{\ast }(V_{s},Z_{s},q_{s}^{\ast,\xi})|ds]<\infty\), and we easily conclude that \(q^{*,\xi}\in\mathcal{A}^{\prime}_{[0,T]}\). □

5.3 Proof of Proposition 3.8

Let \(\bar{\xi}_{T}:=\xi-\frac{Y_{T}-\lambda T}{\gamma}\in \mathcal{F}_{T}\), with \(Y_{T}\) and \(\lambda\) as in Proposition 2.5. Therefore, the classical utility maximization problem (3.12) with risk position \(\bar{\xi}_{T}\) coincides with (3.2) with risk position \(\xi\), namely,

$$ w^{\bar{\xi}_{T}}(x,t)=u^{\xi}(x,t). $$

It then follows from (5.3) in the proof of Theorem 3.2 that

$$ w^{\bar{\xi}_{T}}\big(x+\rho_{t,T}(\bar{\xi}_{T}),t\big)=U(x,t)e^{- \gamma\rho_{t,T}(\bar{\xi}_{T})}e^{\gamma Y_{t}^{-\xi}}. $$

In turn, Definition 3.7 implies that

$$ w^{0}(x,t)=U(x,t)e^{-\gamma\rho_{t,T}(\bar{\xi}_{T})}e^{\gamma Y_{t}^{-\xi}}. $$
(5.11)

Taking \(\xi=0\) in (5.11) further yields that

$$ w^{0}(x,t)=U(x,t)e^{-\gamma\rho_{t,T}(-\frac{Y_{T}-\lambda T}{\gamma})}e^{\gamma Y_{t}^{0}}. $$
(5.12)

Therefore, combining (5.11) and (5.12) gives

$$ Y_{t}^{-\xi}-Y_{t}^{0}=\rho_{t,T}(\bar{\xi}_{T})-\rho_{t,T}\left (-\frac{ Y_{T}-\lambda T}{\gamma}\right). $$

However, by Theorem 3.2, we know that \(Y_{t}^{-\xi}=\rho_{t}(\xi)\), and if \(\xi=0\) in the BSDE (3.4), it is obvious that its solution is \(Y_{t}^{0}=0\), from which we conclude.  □

5.4 Proof of Theorem 3.10

We first establish some auxiliary estimates for the function \(y^{T,g}: \mathbb{R}^{d}\times[0,T]\rightarrow\mathbb{R}\) appearing in (3.15).

Lemma 5.2

Consider an arbitrary risk position\(\xi\)as in (3.14) with maturity\(T\)and the function\(y^{T,g}( \cdot,\cdot) \)as in (3.15). Suppose that Assumptions 2.1, 2.2and 3.9hold. Then for\((v,t)\in \mathbb{R}^{d}\times[0,T]\), the function\(y^{T,g}(\cdot,\cdot)\)has the following properties:

(i) There exists a constant\(C>0\)such that

$$ |y^{T,g}(v,t)|\leq C(1+|v|). $$

(ii) With the constants\(K\)as in (A.3), \(C_{v}\)in (5.1) and\(C_{\eta}\)in Assumption 2.2(i),

$$ |\nabla y^{T,g}(v,t)|\leq K+\frac{C_{v}}{\gamma(C_{\eta}-C_{v})}. $$

(iii) There exists a constant\(C>0\)such that for\(v,\bar{v}\in \mathbb{R} ^{d}\),

$$ |y^{T,g}(v,t)-y^{T,g}(\bar{v},t)|\leq C(1+|v|^{2}+|\bar{v}|^{2})e^{-\hat{C} _{\eta}(T-t)}, $$

with the constant\(\hat{C}_{\eta}\)given in Proposition 2.3.

Proof

Fix \(t\in[0,T]\), and let the stochastic factor process start at \(V_{t}=v\). We use the self-evident notation \(V_{s}^{t,v}\) for \(s\in[ t,T]\). Recall from Proposition 2.5 the solution \((Y_{s},Z_{s})=(y(V_{s}^{t,v}),z(V_{s}^{t,v}))\). Furthermore, for \(s\in [ t,T]\), we also have for the solution \((Y_{s}^{-\xi },Z_{s}^{-\xi})\) of (3.4) that

$$ (Y_{s}^{-\xi},Z_{s}^{-\xi })=\big(y^{T,g}(V_{s}^{t,v},s),z^{T,g}(V_{s}^{t,v},s)\big), $$

where

$$\begin{aligned} Y_{s}^{-\xi} =&g(V_{T}^{t,v})+\int_{s}^{T}\frac{1}{\gamma}\Big( F\big(V_{u}^{t,v},\gamma\hat{z}(V_{u}^{t,v},u)\big)-F(V_{u}^{t,v},Z_{u})\Big) du \\ &-\int_{s}^{T}\left( \hat{z}(V_{u}^{t,v},u)-\frac{Z_{u}}{\gamma}\right) ^{\mathrm{tr}}dW_{u}, \end{aligned}$$
(5.13)

with

$$ \hat{z}(V_{s}^{t,v},s):=Z_{s}^{-\xi}+\frac{Z_{s}}{\gamma} =z^{T,g}(V_{s}^{t,v},s)+\frac{z(V_{s}^{t,v})}{\gamma}. $$
(5.14)

In Lemma A.1 of the Appendix, we show that \(|\hat{z}(\cdot,\cdot)|\leq K\) for a constant \(K\) given in (A.3). Therefore, the process \(Z^{-\xi}\) is uniformly bounded since

$$ |Z_{s}^{-\xi}|=\left\vert\hat{z}(V_{s}^{t,v},s)-\frac{Z_{s}}{\gamma }\right\vert\leq K+\frac{ C_{v}}{\gamma(C_{\eta}-C_{v})}. $$

In turn, the estimate ii) for \(y^{T,g}(v,t)\) follows from \(\kappa^{\mathrm{tr} }\nabla y^{T,g}(V_{s}^{t,v},s)=Z_{s}^{-\xi}\) for \(s\in[t,T]\) and the conditions on the matrix \(\kappa\).

To prove (i), we introduce the process

$$\begin{aligned} H(V_{s}^{t,v})&:=\frac{( F(V_{s}^{t,v},\gamma\hat{z} (V_{s}^{t,v},s))-F(V_{s}^{t,v},Z_{s})) ( \hat{z}(V_{s}^{t,v},s)- \frac{Z_{s}}{\gamma}) }{\gamma \vert\hat{z}(V_{s}^{t,v},s)- \frac{Z_{s}}{\gamma} \vert^{2}} \\ &\phantom{=::}\times\mathbf{1}_{ \{ \hat{z} (V_{s}^{t,v},s)-\frac{Z_{s}}{\gamma}\neq0 \} } \end{aligned}$$
(5.15)

and observe that it is uniformly bounded due to (5.2) and the boundedness of \(\hat{z}(\cdot,\cdot)\) and \(Z\). Next, define a probability measure \(\mathbb{Q}^{H}\) by \(\frac{d\mathbb{Q}^{H}}{d\mathbb{P}}|_{\mathcal{F}_{T}}=\mathcal{E}(\int _{t}^{\cdot }(H(V_{s}^{t,v}))^{\mathrm{tr}}dW_{s})_{T}\). Then (5.13) can be written as

$$\begin{aligned} Y_{t}^{-\xi}&=y^{T,g}(v,t) \\ &=g(V_{T}^{t,v})-\int_{t}^{T}\left( \hat{z}(V_{s}^{t,v},s)-\frac {Z_{s}}{\gamma}\right) ^{\mathrm{tr}}\big(dW_{s}-H(V_{s}^{t,v})ds\big) \\ &=E_{\mathbb{Q} ^{H}}[g(V_{T}^{t,v})|\mathcal{F}_{t}], \end{aligned}$$
(5.16)

and the assertion follows from the linear growth property of \(g(\cdot)\) and the first assertion of part (ii) in Proposition 2.3.

Finally, for \(v,\bar{v}\in\mathbb{R}^{d}\), by the second assertion of (ii) in Proposition 2.3,

$$\begin{aligned} |y^{T,g}(v,t)-y^{T,g}(\bar{v},t)| =&\big\vert E_{\mathbb{Q} ^{H}}[g(V_{T}^{t,v})-g(V_{T}^{t,\bar{v}})|\mathcal{F}_{t}]\big\vert \\ =&\big\vert E_{\mathbb{Q}^{H}}[g(V_{T-t}^{0,v})-g(V_{T-t}^{0,\bar{v} })]\big\vert \\ \leq& C( 1+|v|^{2}+|\bar{v}|^{2}) e^{-\hat{C}_{\eta}(T-t)}, \end{aligned}$$

and we conclude. □

Proof of Theorem 3.10

(i) Using estimate (i) in Lemma 5.2, we first construct—applying a standard diagonal procedure—a sequence \((T_{i})_{i=1}^{\infty}\) such that \(T_{i}\uparrow\infty\) and \(\lim_{T_{i}\uparrow\infty}y^{T_{i},g}( v,0) =\)\(L^{g}( v) \), \(v\in D\), for some function \(L^{g}( v) \) and a dense subset \(D\) of \(\mathbb{R}^{d}\). Moreover, estimate (ii) in Lemma 5.2 implies that for any \(v,\bar{v}\in\mathbb{R}^{d}\),

$$ |y^{T,g}( v,0) -y^{T,g}( \bar{v},0) |\leq\left( K+ \frac{C_{v}}{\gamma(C_{\eta}-C_{v})}\right) |v-\bar{v}|. $$
(5.17)

Therefore, the limit function \(L^{g}(v)\) can be extended to a Lipschitz-continuous function defined for all \(v\in\mathbb{R}^{d}\). Furthermore, we claim that

$$ \lim_{T_{i}\uparrow\infty}y^{T_{i},g}(v,0)=L^{g}(v),\qquad v\in \mathbb{R}^{d}. $$

Indeed, for \(v\in\mathbb{R}^{d}\backslash D\), there exists a sequence \((v_{j})_{j=1}^{\infty}\subseteq D\) such that \(v_{j}\rightarrow v\). For \(v\in\mathbb{R}^{d}\backslash D\), then define \(L^{g}( v) =\lim_{j\uparrow\infty}L^{g}( v_{j}) \). Using (5.17), we have

$$ |y^{T_{i},g}( v,0) -y^{T_{i},g}( v_{j},0) |\leq\left( K+\frac{C_{v}}{\gamma(C_{\eta}-C_{v})}\right) |v-v_{j}|. $$

Taking \(T_{i}\uparrow\infty\) and since \(\lim_{T_{i}\uparrow\infty }y^{T_{i},g}( v_{j},0) =L^{g}( v_{j}) \), we obtain

$$ \left\vert\lim_{T_{i}\uparrow\infty}y^{T_{i},g}( v,0) -L^{g}( v_{j}) \right\vert\leq\left( K+\frac{C_{v}}{\gamma (C_{\eta}-C_{v})}\right) |v-v_{j}|. $$

Sending \(j\uparrow\infty\), we deduce that for any \(v\in\mathbb {R}^{d}\), \(\lim_{T_{i}\uparrow\infty}y^{T_{i},g}( v,0) =L^{g}( v) \).

Next, we show that for any \(v\in\mathbb{R}^{d}\), the limit \(L^{g}(v)\) actually satisfies \(L^{g}(v)\equiv L^{g}\), with \(L^{g}\) being a constant. To this end, by estimate (iii) in Lemma 5.2, we have for any \(v,\bar{v}\in\mathbb{R}^{d}\) that

$$ |y^{T_{i},g}( v,0) -y^{T_{i},g}( \bar{v},0) |\leq C( 1+|v|^{2}+|\bar{v}|^{2}) e^{-\hat{C}_{\eta}T_{i}}. $$

Letting \(T_{i}\uparrow\infty\) yields that \(\lim_{T_{i}\uparrow\infty }y^{T_{i},g}( v,0) =\lim_{T_{i}\uparrow\infty}y^{T_{i},g}( \bar{v},0) \), which implies that the limit function \(L^{g}(v)\) is independent of \(v\). Thus, it is a constant, denoted by \(L^{g}\). Moreover, such a constant \(L^{g}\) is independent of the choice of the sequence \((T_{i})_{i=1}^{\infty}\) (see for example [19, Theorem 4.4] for a proof).

To prove the convergence rate (3.16), we argue as follows. For \(v\in\mathbb{R}^{d}\) and \(T>0\), we have from (5.16) in the proof of Lemma 5.2(i) that

$$\begin{aligned} |y^{T,g}( v,0) -L^{g}| =& \lim_{T^{\prime}\uparrow \infty}|y^{T,g}( v,0) -y^{T^{\prime},g}( v,0) |\\ =& \lim_{T^{\prime}\uparrow\infty} \vert y^{T,g}( v,0) -E_{ \mathbb{Q}^{H}}[ g(V_{T^{\prime}}^{0,v})] \vert. \end{aligned}$$

For \(T^{\prime}>T\), we then have from the tower property of conditional expectations that

$$\begin{aligned} \vert y^{T,g}( v,0) -E_{ \mathbb{Q}^{H}}[ g(V_{T^{\prime}}^{0,v})] \vert =&\big\vert y^{T,g}( v,0) -E_{ \mathbb{Q}^{H}}\big[ E_{\mathbb{Q}^{H}}[ g(V_{T^{\prime}}^{0,v})\vert \mathcal{F}_{T^{\prime}-T}] \big] \big\vert \\ =& \vert y^{T,g}( v,0) -E_{ \mathbb{Q}^{H}}[ y^{T^{\prime},g}( V_{T^{\prime }-T}^{0,v},T^{\prime}-T) ] \vert \\ =& \vert y^{T,g}( v,0) -E_{ \mathbb{Q}^{H}}[ y^{T,g}( V_{T^{\prime}-T}^{0,v},0) ] \vert\\ =& \vert E_{\mathbb{Q}^{H}}[ y^{T,g}( v,0) -y^{T,g}( V_{T^{\prime}-T}^{0,v},0) ] \vert. \end{aligned}$$

Therefore,

$$\begin{aligned} |y^{T,g}( v,0) -L^{g}| =&\lim_{T^{\prime}\uparrow\infty } \vert E_{\mathbb{Q}^{H}}[ y^{T,g}( v,0) -y^{T,g}( V_{T^{\prime}-T}^{0,v},0) ] \vert\\ \leq&\lim_{T^{\prime}\uparrow\infty}CE_{\mathbb{Q}^{H}}[ 1+|v|^{2}+ \vert V_{T^{\prime}-T}^{0,v} \vert^{2}] e^{-\hat{ C}_{\eta}T}\\ \leq& C( 1+|v|^{2}) e^{-\hat{C}_{\eta}T}, \end{aligned}$$

where in the last two inequalities, we used part (ii) of Proposition 2.3 and part (iii) of Lemma 5.2.

(ii) We only establish the exponential bound (3.17), since the asymptotic behavior of \(\alpha _{t,T}\) in (3.18) will then follow by letting \(T\uparrow\infty\).

From Corollary 3.4 and the Lipschitz-continuity of the projection operator on the convex set \(\Pi\), we deduce that for any \(s\in [0,T)\),

$$\begin{aligned} &E_{\mathbb{P}}\left[\int_{0}^{s}|\alpha_{u,T}|^{2}du\right]\\ &= E_{\mathbb{P}}\bigg[\int_{0}^{s}\left|\mathrm{Proj}_{\Pi}\left(Z_{u}^{-\xi}+\frac {\theta(V_{u})+Z_{u}}{\gamma}\right)- \mathrm{Proj}_{\Pi}\left(\frac{\theta(V_{u})+Z_{u}}{\gamma}\right)\right|^{2}du\bigg]\\ &\leq C E_{ \mathbb{P}}\left[ \int_{0}^{s}|Z_{u}^{-\xi}|^{2}du\right] \end{aligned}$$

for some constant \(C\) independent of \(T\). Thus, we only need to establish the exponential bound of \(Z_{u}^{-\xi}=z^{T,g}(V_{u}^{v},u)\) with the stochastic factor process starting from \(V_{0}^{v}=v\). To this end, we easily deduce, using (iii) in Lemma 5.2, that for \(t\in [ 0,T)\),

$$ |y^{T,g}(v,t)-L^{g}|\leq C(1+|v|^{2})e^{-\hat{C}_{\eta}(T-t)}. $$
(5.18)

Applying Itô’s formula to \(|y^{T,g}(V_{s}^{v},s)-L^{g}|^{2}\) and using (5.13), we in turn have

$$\begin{aligned} &|y^{T,g}(v,0)-L^{g}|^{2}+E_{\mathbb{P}}\left[ \int_{0}^{s}|Z_{u}^{-\xi }|^{2}du\right]\\ &=E_{\mathbb{P}}[|y^{T,g}(V_{s}^{v},s)-L^{g}|^{2}] \\ &\phantom{=:}+ 2E_{\mathbb{P}}\left[ \int _{0}^{s}|y^{T,g}(V_{u}^{v},u)-L^{g}|\frac{ F(V_{u}^{v},\gamma\hat{z}(V_{u}^{v},u))-F(V_{u}^{v},Z_{u})}{\gamma}du \right] \\ &=E_{\mathbb{P}}[|y^{T,g}(V_{s}^{v},s)-L^{g}|^{2}]+2E_{\mathbb{P}}\left[ \int_{0}^{s}(Z_{u}^{-\xi})^{\mathrm{tr}}H(V_{u}^{v})|y^{T,g}(V_{u}^{v},u)-L^{g}|du \right] , \end{aligned}$$

where \(\hat{z}(\cdot,\cdot)\) is given in (5.14) and the process \(H(V_{u}^{v})\), introduced in (5.15), is uniformly bounded. Using the elementary inequality \(ab\leq\frac{1}{4}|a|^{2}+|b|^{2}\), we further obtain

$$\begin{aligned} &E_{\mathbb{P}}\left[ \int_{0}^{s}(Z_{u}^{-\xi })^{\mathrm{tr}}H(V_{u}^{v})|y^{T,g}(V_{u}^{v},u)-L^{g}|du\right] \\ &\leq\frac{1}{4}E_{\mathbb{P}}\left[ \int_{0}^{s}|Z_{u}^{-\xi}|^{2}du \right] +CE_{\mathbb{P}}\left[ \int_{0}^{s}|y^{T,g}(V_{u}^{v},u)-L^{g}|^{2}du \right] . \end{aligned}$$

Hence, (5.18) yields that

$$\begin{aligned} &\frac{1}{2}E_{\mathbb{P}}\left[ \int_{0}^{s}|Z_{u}^{-\xi _{T}}|^{2}du\right]\\ &\leq E_{\mathbb{P}}[|y^{T,g}(V_{s}^{v},s)-L^{g}|^{2}]+CE_{\mathbb{P}}\left[ \int_{0}^{s}|y^{T,g}(V_{u}^{v},u)-L^{g}|^{2}du\right]\\ &\leq Ce^{-2\hat{C}_{\eta}T}\left( e^{2\hat{C}_{\eta}s}E_{\mathbb{P} }[(1+|V_{s}^{v}|^{2})^{2}]+\int_{0}^{s}e^{2\hat{C}_{\eta}u}E_{\mathbb{P} }[(1+|V_{u}^{v}|^{2})^{2}]du\right) , \end{aligned}$$

from which we conclude that \(E_{\mathbb{P}}[ \int_{0}^{s}|Z_{u}^{-\xi }|^{2}du] \leq C(1+|v|^{4})e^{-2\hat{C}_{\eta}(T-s)}\), using the first assertion of part (ii) in Proposition 2.3. □

6 Conclusions and extensions

We have studied forward entropic risk measures for stochastic factor models and in the presence of trading constraints. Using the ergodic BSDE representation of the involved exponential forward performance processes, we have established two representation results, working with the primal and the dual domains, respectively. We have also derived a parity result between the forward entropic risk measures and their classical counterparts, and moreover investigated their asymptotic behavior for large maturities.

The approach and the results herein may be extended in several directions. Firstly, one may allow stochastically evolving set of constraints. This is undoubtedly a very important extension, for trading constraints in many applications are affected by upcoming (and frequently, non-anticipated) market changes, past performance and other features that the forward performance criteria may accommodate. To the best of our knowledge, this generalization has not been considered so far in the context of forward performance criteria.

Another important issue is the relative valuation and risk management of incoming projects. Herein, we consider the measurement of risk positions with arbitrary maturities, but in isolation from each other. In various applications, however, one needs to price incoming projects in relation to existing ones, and work with relative risk assessment. In order to do this, one first needs to define properly “relative” forward performance processes, which will naturally depend on the evolving risks associated with the existing projects. Such extensions are left for future research.