1 Introduction

Ships are usually equipped with a gyrocompass, which is a nonmagnetic compass based on a fast-spinning disc (Fossen [1]). A north-seeking gyro gives a highly accurate measurement of the heading (yaw) angle, and this is the preferred sensor from the safety point of view. Smaller boats cannot afford to use expensive sensors such as gyrocompasses. An alternative could be to use a magnetic compass. However, magnetic compasses are not used on-board commercial ships as navigational devices since they are susceptible to magnetic disturbances. A magnetic compass is, in fact, an extremely simple device. It consists of a small, lightweight magnet balanced on a nearly frictionless pivot point. However, the magnetic field of the Earth is not perfectly aligned along the Earth’s rotational axis. It is skewed slightly off-center. This skew or bias is called declination, and it must be compensated for. Sensitivity to magnetic variations and declination causes significant problems when designing path-following control systems.

An alternative measurement could be to use two GNSS antennas on the same receiver with a known offset vector to compute the heading angle. However, this method requires good GNSS signal reception and it can be sensitive to ionospheric disturbances, multipath, loss of signals, the number of available satellites, etc.

Suppose the heading angle is available as a measurement. In that case, it is straightforward to design a proportional-integral-derivative (PID) controller for path-following control using a conventional heading autopilot (see Fossen [1]). However, the objective of this article is to discuss an alternative low-cost path-following controller for ships using course autopilots. The motivation for this is to avoid using an expensive gyrocompass, an unreliable magnetic compass, or two GNSS antennas (Farrell [2]) when designing ship path-following control systems. To succeed, it is necessary to employ a robust algorithm for estimating the ship’s COG, SOG, and course rate. These are the main signals needed to implement the LOS path-following guidance law of Lekkas and Fossen [3], or the vector-field guidance law of Nelson et al. [4] both utilizing the course angle for feedback.

Li and Jilkov [5] have reviewed dynamic models for target tracking in 2D and 3D. The simplest models for a targeting maneuver are the white-noise constant velocity (CV) and constant acceleration (CA) models (Bar-Shalom et al. [6]). In this work, it is assumed that the target velocity \(\dot{x} = w\) or acceleration \(\ddot{x} = w\) are independent processes driven by Gaussian white noise w. The CV model works well for ship path-following control since the velocity is nearly constant even though the ship experiences small accelerations. The CA model can be used to describes more aggressive maneuvers (Li and Jilkov [5]).

When a moving ship or a target’s trajectory satisfies a kinematic constraint, the kinematic constraint can be utilized as additional information about the ship to improve the tracking of the time-varying velocity and bearing. Tahk and Speyer [7] proposed to incorporate the kinematic constraints as pseudomeasurements. Using the kinematic constraint, it is possible to remove some of the uncertainty of the time-varying velocities and force the velocity estimates to change consistently with the dynamics of a moving ship. A formulation of the kinematic constraint for constant speed has been presented by Alouani and Blair [8] where the filter utilizes pseudomeasurements to obtain unbiased estimates. The EKF presented in this article uses a CV model for the speed dynamics, while the course angle dynamics is modeled as a CA model to obtain estimates of both the course angle and the course rate (Fossen and Fossen [9]). The North—East velocity equations of the ship are represented by amplitude and phase to avoid that the yaw angle enters the kinematic equations of motion and at the same time preserve the kinematic constraints for a moving object in 2D. This ensures that the speed and course angle satisfy the kinematic constraints when estimated in an EKF. This is important to obtain accurate estimates of the COG and the SOG.

The remainder of this article is organized as follows: Sect. 2 presents the kinematic equations and EKF for COG, SOG, and course rate estimation. Section 3 presents the LOS path-following controller utilizing a course autopilot system. Section 4 contains a simulation study of a MARINER class cargo ship in a path-following scenario. The concluding remarks are drawn in Sect. 5.

2 Estimation of COG, SOG and course rate

This section contains the kinematic preliminaries and EKF for estimation of COG, SOG, and course rate.

Fig. 1
figure 1

Ocean current triangle

Full size image

2.1 Kinematic preliminaries

The relationship between the angular variables course, heading and sideslip is important for ship maneuvering. The terms course and heading are used interchangeably in much of the literature on guidance, navigation and control of marine craft, and this leads to confusion. Let the BODY and North-East-Down (NED) references frame in Fig. 1 be denoted \(\{ b \} = (x_b, \, y_b, \, z_b)\) and \(\{ n \} = (x_n, \, y_n, \, z_n)\), respectively. Then, the following definitions can be made:

Definition 1

(Yaw or heading angle \({{\psi }}\)) The angle \(\psi\) from the \(x_{n}\) axis (true North) to the \(x_{b}\) axis of the ship, positive rotation about the \(z_{n}\) axis by the right-hand screw convention.

The heading angle is usually measured using a magnetic compass, gyrocompass, or two GNSS receivers; see Gade [10] for a discussion on methods. The heading angle is well defined for zero speed such that it is possible to design a heading autopilot to maintain constant heading during stationkeeping and transit. However, during transit, it is common to use a course autopilot for path following. For small vehicles and boats, the gyrocompass is expensive, while it is difficult to use a magnetic compass since it is prone to electromagnetic disturbances. This makes course autopilots for path-following control a preferred solution, provided that the course angle can be accurately estimated.

Definition 2

(Course angle \({{\chi }}\,\)) The angle \(\chi\) from the \(x_{n}\) axis (true North) to the velocity vector of the ship, positive rotation about the \(z_{n}\) axis by the right-hand screw convention.

Note that the course angle is only defined for positive speed.

The North–East positions \((x^n, \, y^n)\) of a ship can be described by (see Fossen [1])

$$\begin{aligned} \dot{x}^n&= u \cos (\psi ) - v \sin (\psi ) \end{aligned}$$
(1)
$$\begin{aligned} \dot{y}^n&= u \sin (\psi ) + v \cos (\psi ), \end{aligned}$$
(2)

where \((u, \, v)\) are the surge and sway velocities, respectively. Equations (1)–(2) can be expressed in amplitude-phase form by

$$\begin{aligned} \dot{x}^n&= U \cos \left( \psi + \beta _\mathrm{c}\right) := U \cos (\chi ) \end{aligned}$$
(3)
$$\begin{aligned} \dot{y}^n&= U \sin \left( \psi + \beta _\mathrm{c}\right) := U \sin (\chi ), \end{aligned}$$
(4)

where the course angle is defined as

$$\begin{aligned} \chi := \psi +\beta _\mathrm{c}. \end{aligned}$$
(5)

Further, the amplitude U and phase variable \(\beta _\mathrm{c}\) are

$$\begin{aligned} U&=\sqrt{u^{2}+v^{2}} \end{aligned}$$
(6)
$$\begin{aligned} \beta _\mathrm{c}&= \mathrm {atan} \left( \frac{v}{u} \right) = \sin ^{-1} \left( \frac{v}{U} \right) . \end{aligned}$$
(7)

These quantities are recognized as the speed in the horizontal plane and the crab angle, respectively.

Definition 3

(Crab angle \({{\beta }_\mathrm{c}}\)) The angle \(\beta _\mathrm{c}\) from the \(x_{b}\) axis to the velocity vector of the ship, positive rotation about the \(z_{b}\) axis by the right-hand screw convention.

A ship is exposed to ocean currents. Let \((u_{\mathrm{c}}, \, v_{\mathrm{c}})\) denote the velocity components of an irrotational current. Hence, the ocean current speed is (see Fig. 1),

$$\begin{aligned} U_\mathrm{c} = \sqrt{u _\mathrm{c}^2 + v_\mathrm{c}^2}, \end{aligned}$$
(8)

and the relative speed is

$$\begin{aligned} U_{\mathrm{r}}=\sqrt{u_\mathrm{r}^2 + v_\mathrm{r}^2 }, \end{aligned}$$
(9)

where \(u_{\mathrm{r}} = u-u_{\mathrm{c}}\) and \(v_{\mathrm{r}} = v-v_{\mathrm{c}}\). Figure 1 shows the sideslip angle

$$\begin{aligned} \beta = \sin ^{-1}\left( \frac{v_\mathrm{r}}{U_\mathrm{r}}\right) , \end{aligned}$$
(10)

for a ship as defined below.

Definition 4

(Sideslip angle \({{\beta }}\)) The angle \(\beta\) from the \(x_{b}\) axis to the relative velocity vector of the ship, positive rotation about the \(z_{b}\) axis by the right-hand screw convention.

2.2 Five-state extended Kalman filter

The primary objective of the EKF is to compute accurate estimates of the COG and SOG of the ship when moving along the path (Fossen and Fossen [9]). In addition, it is desirable to calculate an estimate of the course rate. It is essential that the estimates are properly filtered and that old data points (memory effects) are included in the filter. This is the primary motivation for using the Kalman filter. Since the path is not parametrized, the only information during path following is the ship’s North and East positions, which are assumed measured by a GNSS receiver. The North–East positions \((x^n, y^n)\) of a ship are given by the kinematic equations (3) and (4), while the speed U can be modeled by a CV model driven by white noise. The course angle \(\chi\) is modeled as a CA model to obtain estimates of the course rate \(\dot{\chi } = \omega _{\chi }\). This corresponds to using white-noise-driven double and triple integrators in the target-tracking literature, see Li and Jilkov [5].

Simulation studies revealed that the CV and CA models were most accurate for ship path following since the speed and course rate are nearly constant most of the time. The only observed changes of speed and course rate are when the ship turns in the vicinity of a waypoint. The EKF is implemented using Cartesian coordinates \((x^n, y^n)\) under a flat-Earth assumption. For global navigation applications the longitude-latitude representation should be used as described by Fossen and Fossen [9].

State-space model The resulting state-space model expressed in Cartesian coordinates is

$$\begin{aligned} \dot{x}^n&= U \cos (\chi ) \end{aligned}$$
(11)
$$\begin{aligned} \dot{y}^n&= U \sin (\chi ) \end{aligned}$$
(12)
$$\begin{aligned} \dot{U}&= -\alpha _1 U + w_1 \end{aligned}$$
(13)
$$\begin{aligned} \dot{\chi }&= \omega _\chi \end{aligned}$$
(14)
$$\begin{aligned} \dot{\omega _\chi }&= -\alpha _2 \omega _\chi + w_2, \end{aligned}$$
(15)

where \(w_1\) and \(w_2\) are Gaussian white-noise processes, and where two small constants \(\alpha _1 > 0\) and \(\alpha _2 > 0\) have been added to the model to ensure that U and \(\omega _\chi\) converge to zero during dead reckoning and stationkeeping. Equations (13) and (15) are referred to as Singer models [11] in the target-tracking community. The corresponding North-East GNSS position measurements are

$$\begin{aligned} y_1&= x^n + \varepsilon _1 \end{aligned}$$
(16)
$$\begin{aligned} y_2&= y^n + \varepsilon _2 , \end{aligned}$$
(17)

where \(\varepsilon _1\) and \(\varepsilon _2\) are Gaussian white-noise processes. The state and noise vectors corresponding to (11)–(15) and (16)–(17) are

$$\begin{aligned} \varvec{x}&= \left[ x^n, y^n, U, \chi , \omega _\chi \right] ^\top \end{aligned}$$
(18)
$$\begin{aligned} \varvec{y}&= \left[ x^n, y^n \right] ^\top \end{aligned}$$
(19)
$$\begin{aligned} \varvec{w}&= \left[ w_1, w_2 \right] ^\top \end{aligned}$$
(20)
$$\begin{aligned} \varvec{\varepsilon }&= \left[ \varepsilon _1, \varepsilon _2 \right] ^\top . \end{aligned}$$
(21)

Consequently, the discrete-time state-space model can be expressed as

$$\begin{aligned} \varvec{x}[k+1]&= \varvec{A}_d \, \varvec{x}[k] + \varvec{E}_d \varvec{w}[k] \end{aligned}$$
(22)
$$\begin{aligned} \varvec{y}[k]&= \varvec{C}_d \varvec{x}[k] + \varvec{\varepsilon }[k], \end{aligned}$$
(23)

where

$$\begin{aligned} \varvec{A}_d&= \left[ \begin{array}{ccccc} 1 &{} 0 &{} h \cos \left( \hat{x}_4[k]\right) &{} -h \, \hat{x}_3[k] \sin \left( \hat{x}_4[k]\right) &{} 0 \\ 0 &{} 1 &{} h \sin \left( \hat{x}_4[k]\right) &{} h \, \hat{x}_3[k] \cos \left( \hat{x}_4[k]\right) &{} 0 \\ 0 &{} 0 &{} 1- h \alpha _1 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 1 &{} h \\ 0 &{} 0 &{} 0 &{} 0 &{} 1- h \alpha _2 \\ \end{array} \right] \end{aligned}$$
(24)
$$\begin{aligned} \varvec{E}_d&= \left[ \begin{array}{cc} 0 &{} 0 \\ 0 &{} 0 \\ h &{} 0 \\ 0 &{} 0 \\ 0 &{} h \end{array} \right] , \qquad \varvec{C}_d = \left[ \begin{array}{ccccc} 1 &{} 0 &{} 0 &{} 0 &{} 0\\ 0 &{} 1 &{} 0 &{} 0 &{} 0 \end{array} \right] . \end{aligned}$$
(25)

The model is discretized using Euler’s method and h denotes the sampling time. The resulting EKF algorithm for (22) and (23) is summarized in Table 1 where \(\varvec{Q}_d[k]\) and \(\varvec{R}_d[k]\) are the covariance matrices for the process and measurement noises (see Brown and Hwang [12]). The a priori state and covariance matrix estimates (before update) are denoted \((\hat{\varvec{x}}^{-}[k], \, \hat{\varvec{P}}^{-}[k])\) while the a posteriori state and covariance matrix estimates (after update) are denoted by \((\hat{\varvec{x}}[k], \, \hat{\varvec{P}}[k])\).

Table 1 Discrete-time EKF for estimation of SOG and COG
Full size table
Fig. 2
figure 2

Block diagram showing the LOS guidance law and course autopilot loops. The EKF produces estimates of the COG, SOG and course rate

Full size image

3 LOS path following using course control

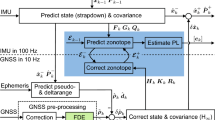
The control system is implemented as two successive loops as shown in Fig. 2. The guidance law and course autopilot are presented below.

3.1 Course autopilot

The course angle dynamics is approximated by a first-order model (Nomoto et al. [13])

$$\begin{aligned} {\dot{\chi }}&= \omega _\chi \end{aligned}$$
(26)
$$\begin{aligned} \dot{\omega }_\chi&= - \frac{1}{T} \omega _\chi + \frac{K}{T} \delta + d_\omega , \end{aligned}$$
(27)

where \(\delta\) is the rudder angle and \(d_\omega\) is a constant disturbance due to unmodeled dynamics and environmental disturbances. In practice, \(d_\omega\) will be a nearly constant drift term but an integral controller will be able to compensate for drift. The Nomoto gain and time constant K and T, respectively can be determined by a maneuvering test. e.g. a turning circle or a zigzag test or system identification (Fossen [1]). Note that the yaw rate r of the ship relates to the course rate \(\omega _\chi\) by

$$\begin{aligned} r := \omega _\chi - \dot{\beta }_\mathrm{c}. \end{aligned}$$
(28)

This follows directly from (5).

The course autopilot is chosen as a PID controller with reference feeforward

$$\begin{aligned} \delta = \tau _\mathrm{FF} -K_p \left( \text {ssa}(\tilde{\chi}) - \frac{1}{T_i} \int _0^t \text {ssa}(\tilde{\chi}) \text {d}\tau - T_d \tilde{\omega }_\chi \right) , \end{aligned}$$
(29)

where \(\delta\) is the commanded rudder angle, \(K_p\) is the proportional gain, \(T_d\) is the derivative time constant and \(T_i\) is the integral time constant. The course rate tracking error is denoted by \(\tilde{\omega }_\chi = \omega _\chi - \omega _{\chi _d}\) where the subscript d denotes the desired value. The unconstrained course angle tracking error \(\tilde{\chi } = \chi - \chi _d\) is mapped to the interval \([-\pi , \, \pi )\) using the operator \(\mathrm {ssa:} \, \mathbb {R} \rightarrow [-\pi , \, \pi )\) representing the smallest difference between the two angles \(\chi\) and \(\chi _d\). The MSS Matlab implementation is ssa.m (Fossen and Perez [14]).

The reference feedforward term is chosen as

$$\begin{aligned} \tau _\mathrm{FF} = \frac{T}{K} \dot{\omega }_{\chi _d} + \frac{1}{T} \omega _{\chi _d}, \end{aligned}$$
(30)

where \(\omega _{\chi _d}\) and \(\dot{\omega }_{\chi _d}\) are the desired angular velocity and acceleration, respectively.

The resulting closed-loop system is

$$\begin{aligned}&\ddot{\tilde{\chi }} + \left( \frac{1}{T} + \frac{K K_p T_d}{T} \right) \dot{\tilde{\chi }} + \frac{K K_p}{T} \text {ssa}\left( \tilde{\chi }\right) \nonumber \\&\quad + \frac{K K_p}{TT_i} \int _0^t \text {ssa}\left( \tilde{\chi }\right) \text {d}\tau = d_\omega . \end{aligned}$$
(31)

The controller gains can be determined by pole placement with \(\omega _n\) and \(\zeta\) as design parameters. This gives

$$\begin{aligned} \frac{K K_p}{T}&:= \omega _n^2 \implies K_p = \frac{T}{K} \omega _n^2 \end{aligned}$$
(32)
$$\begin{aligned} \frac{1}{T} + \frac{K K_p T_d}{T}&:= 2 \zeta \omega _n \implies T_d = \frac{T}{KK_p} \left( 2 \zeta \omega _n - \frac{1}{T} \right) . \end{aligned}$$
(33)

The integrator time constant is chosen such that \(1/T_i = \omega _n/10\). In other words,

$$\begin{aligned} T_i = \frac{10}{\omega _n}. \end{aligned}$$
(34)

This guarantees that the tracking errors \(\tilde{\chi }\) and \(\tilde{\omega }_\chi\) converge exponentially to zero under the assumption of \(\dot{d}_\omega =0\).

Fig. 3
figure 3

LOS geometry showing the desired course angle \(\chi _d\) and the cross-track error \(y_e^p\) expressed in the path-tangential coordinate system \(\{p\}\)

Full size image

3.2 LOS path-following guidance law

For a path made up of straight-line segments, the desired course angle \(\chi _d\) can be computed using the proportional LOS guidance law (Lekkas and Fossen [3]),

$$\begin{aligned} \chi _d&= \pi _p - \tan ^{-1} \left( K_p \, y_e^p \right) , \qquad K_p = \frac{1}{\varDelta }, \end{aligned}$$
(35)

where the proportional gain \(K_p\) is parametrized in terms of the look-ahead distance \(\varDelta > 0\). Formula (35) is easily verified from Fig. 3 where it is seen that the slope of the line segment is \(\pi _p = \chi _{d} + \tan ^{-1} (y_e^p/\varDelta )\). The cross-track error \(y_e^p\) between two successive waypoints \(\varvec{p}_i^n = [x^n_i, \, y^n_i]^\top\) and \(\varvec{p}_{i+1}^n = [x^n_{i+1}, \, y^n_{i+1}]^\top\) is computed by

$$\begin{aligned} y_e^p = -\left( x^n-x_i^n\right) \sin \left( \pi _p\right) + \left( y^n-y_i^n\right) \cos \left( \pi _p\right) , \end{aligned}$$
(36)

where \((x^n, y^n)\) is the ship’s position expressed in NED.

Lyapunov stability analysis Assume that the path-tangential coordinate system \(\{p\}\) has its origin at the waypoint \(\varvec{p}_i^n = [x^n_i, \, y^n_i]^\top\). From this it follows that cross-track error dynamics under the assumption that the course controller ensures perfect tracking, that is \(\chi = \chi _d\), satisfies

$$\begin{aligned} \dot{y}_e^p&= U \sin \left( \chi _p\right) \nonumber \\&= U \sin \left( \chi - \pi _p\right) \nonumber \\&= -U \sin \left( \tan ^{-1} \left( y_e^p/\varDelta \right) \right) \nonumber \\&= - \frac{U}{ \sqrt{\varDelta ^2 + \left( y_e^p\right) ^2 } } \, y_e^p, \end{aligned}$$
(37)

where the trigonometric identity \(\sin (\tan ^{-1}(x)) = x/\sqrt{1+x^2}\) has been applied. Consider the Lyapunov function candidate \(V = 1/2 (y_e^p)^2\). Time differentiation of V and substitution of (37) gives,

$$\begin{aligned} \dot{V}&= - \frac{U}{ \sqrt{\varDelta ^2 + \left( y_e^p\right) ^2 } } \, \left( y_e^p\right) ^2 \nonumber \\&< 0, \qquad \forall y_e^p \ne 0. \end{aligned}$$
(38)

Consequently, the equilibrium point \(y_e^p = 0\) is uniformly semi-globally asymptotically stable (USGES) according to Theorem 1 by Fossen and Pettersen [15].

Reference feedforward The course controller (29) makes use of the feedforward term (30) which depends on \(\omega _{\chi _d}\) and \(\dot{\omega }_{\chi _d}\). Time differentiation of (35) gives

$$\begin{aligned} \omega _{\chi _d}&= -\frac{K_p \dot{y}_e^p}{ \left( K_p y_e^p\right) ^2 + 1} \nonumber \\&= -\frac{K_p U \sin \left( \chi - \pi _p\right) }{ \left( K_p y_e^p\right) ^2 + 1}. \end{aligned}$$
(39)

The desired angular acceleration \(\dot{\omega }_{\chi _d}\) can be computed by time differentiation of (39). However, for practical implementations, it is recommended to use \(\dot{\omega }_{\chi _d}= 0\) since the angular acceleration is a very small number for most ships.

4 Simulation study of a MARINER class cargo ship

The hydrodynamic coefficients of a MARINER class cargo ship, \(L_\mathrm{pp}= 160.9 \, \text {m}\) and \(\nabla = 16,622 \, \text {DWT}\), have been determined by means of a planar motion mechanism (PMM) and compared with the results of full-scale trials by Chislett and Strøm-Tejsen [16]. The resulting model is an m-file, mariner.m, which is implemented in the Marine Systems Simulator (MSS) together with autopilots and LOS guidance laws that can be simulated in Matlab/Simulink (Fossen and Perez [14]). The toolbox also has a Simulink block for simulation of the MARINER m-file; see Fig. 4.

Fig. 4
figure 4

The MSS toolbox Simulink block of the MARINER class cargo ship (Fossen and Perez [14])

Full size image

The EKF covariance matrices were chosen as \(\varvec{P}^-[0] = \varvec{I}_5\), \(\varvec{Q}_d[k] = \mathrm {diag}\{ 0.00001, 0.00001 \}\) and \(\varvec{R}_d[k] = \mathrm {diag}\{ 0.1, 0.1 \}\), while the Singer constants were chosen as \(\alpha _1 = 0.00001\) and \(\alpha _2 = 0.2\). The sampling frequency of the filter was chosen equal to the \(10 \, \mathrm {Hz}\) GNSS measurement frequency corresponding to \(h = 0.1 \, \mathrm {s}\).

The GNSS receiver measurements (North and East positions) were simulated using Gauss-Markov processes based on the model by Beard and McLain [17],

$$\begin{aligned} y_1[k]&= x^n[k] + v_x^n[k] \end{aligned}$$
(40)
$$\begin{aligned} y_2[k]&= y^n[k] + v_y^n[k] \end{aligned}$$
(41)
$$\begin{aligned} v_x^n[k+1]&= e^{-k h} v_x^n[k] + \eta _1[k] \end{aligned}$$
(42)
$$\begin{aligned} v_y^n[k+1]&= e^{-k h} v_y^n[k] + \eta _2[k], \end{aligned}$$
(43)

where \(k = 1/1100~\mathrm{s}^{-1}\) and \(h = 0.1~\mathrm{s}\) is the sampling time. The model is driven by the white-noise terms \(\eta _1\) and \(\eta _2\) with standard deviations of 0.21 m. The model parameters describe a NAVSTAR GPS receiver with standard deviation of 4.7 m.

Fig. 5
figure 5

The ship’s North–East positions when traversing the waypoints. The next waypoint is activated when the remaining distance is \(50 \, \text {m}\)

Full size image

The course controller (29) and feedforward term (30) are implemented by choosing the Nomoto time and gain constants as \(T = 107.3 \, \mathrm {s}\) and \(K= 0.185 \, \mathrm {s}^{-1}\), respectively. The desired course rate is computed by (39) while \(\dot{\omega }_{\chi _d}= 0\). The low-pass filters in Fig. 2 are necessary to avoid jumps in the reference signals \(\chi _d\) and \(\omega _{\chi _d}\) each time a new waypoint is activated. This suggests that

$$\begin{aligned} h_{lp}(s) = \frac{1}{T_{lp}s + 1}, \qquad \frac{1}{T_{lp}} < \omega _n, \end{aligned}$$
(44)

where the filter cut-off frequency \(1/T_\mathrm{lp}\) should be 5-10 times smaller than the natural frequency \(\omega _n\) of the closed-loop course angle dynamics. The PID controller gains are chosen as \(K_p = 1.45\), \(T_d = 36.3 \, \mathrm {s}\) and \(T_i = 200 \, \mathrm {s}\) corresponding to \(\omega _n = 0.05 \, \mathrm {rad s}^{-1}\) and \(\zeta =1.0\). The look-ahead distance was chosen as \(\varDelta = 800 \, \text {m}\). The performance of the LOS guidance law and course autopilot is shown in Fig. 5 where the waypoints are (0, 0), (2000, 0), (5000, 5000), (3000, 8000), (6000, 12, 000) and (10000, 12, 000) are traversed. The next waypoint is activated when the remaining distance to travel is \(R_{\text {switch}} = 50 \, \text {m}\). This is mathematically equivalent to

$$\begin{aligned} d_{i+1} - | x_e^p | \le R_{\text {switch}}, \end{aligned}$$
(45)

where \(d_{i+1} = \Vert \varvec{p}_{i+1}^n -\varvec{p}_i^n \Vert\) is the distance between the waypoints \(\varvec{p}_i^n\) and \(\varvec{p}_{i+1}^n\) and \(x_e^p\) is the along-track error (see Fig. 3),

$$\begin{aligned} x_e^p = \left( x^n-x_i^n\right) \sin \left( \pi _p\right) + \left( y^n-y_i^n\right) \cos \left( \pi _p\right) . \end{aligned}$$
(46)

Figure 6 shows the true, estimated, and desired course angle during path following while Fig. 7 contains the corresponding speeds. The simulation study of the MARINER class cargo ship confirms that the five-state EKF is capable of estimating the COG, SOG, and course rate with great precision during path following. The course autopilot produces non-aggressive rudder angles as shown in Fig. 8. Also note that the rudder rates are less than 5 deg/s during course changing. This confirms that the desired bandwidth of the controller is chosen such that saturation is avoided.

Fig. 6
figure 6

Course angle versus time. The EKF tracking performance is excellent, even during waypoint switching and excessive turning

Full size image
Fig. 7
figure 7

Speed versus time. Note that the speed drops during excessive turning but the EKF tracking performance is still excellent

Full size image
Fig. 8
figure 8

Rudder angle (upper plot) and rudder rate (lower plot) versus time. Note that saturation is avoided when the course controller is tuned using \(\omega _n = 0.05 \, \mathrm {rad s}^{-1}\) and \(\zeta = 1.0\)

Full size image

5 Conclusions

A path-following control system for ships using a course autopilot in conjunction with a proportional line-of-sight (LOS) guidance law has been presented. The primary motivation for using a course autopilot was to avoid the expensive gyrocompass or the unreliable magnetic compass in the feedback loop. Accurate estimates of the ship course angle and speed were obtained by a five-state EKF, which was designed using constant velocity and constant acceleration target-tracking models. Finally, the EKF was applied to a high-fidelity model of a MARINER class cargo ship. The case study was path following and course control using the EKF course angle and course rate estimates. From the simulation study, it can be concluded the EKF successfully estimates the COG and the SOG from GNSS measurements during path following even when using a low-cost GNSS receiver without correction signals. The solution was remarkably robust and accurate when combined with a course autopilot. Hence, the need for a compass was eliminated during path following.