An investigation to identify the thrust in flapping and undulatory motion of smart Timoshenko beam

Abstract

In this paper, a computational approach to investigate the feasibility of using Smart Timoshenko beam (STB) for underwater locomotion is presented. The main objective of the current study is to understand different thrust producing mechanisms, namely flapping and undulatory modes of locomotion and to identify the critical parameters, such as body length, flexural stiffness and tail beat frequency affecting the locomotion. The thrust for different modes of locomotion with a variation in Young’s modulus and moment of inertia for the STB has been calculated. The results will help improve the understanding of thrust generation in both flapping and undulatory modes which are essential in the design and development of the bio-inspired robotic systems for underwater locomotion.

Appendix 1

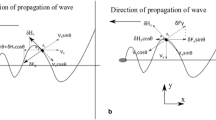
By using the convention and free body diagram from [2]. The Timoshenko beam model is the two-second order coupled partial differential equations of displacement and bending slope indicated. The dynamic equilibrium translation and rotation equations respectively

$$ \frac{{\partial V_{*} }}{\partial x} + \rho A\frac{{\partial^{2} v}}{{\partial t^{2} }} + C_{\text{OD1}} \frac{\partial v}{\partial t} + \frac{1}{2}C_{\text{D}} \rho A\left| {\frac{\partial v}{\partial t}} \right| \times \left| {\frac{\partial v}{\partial t}} \right| = 0 $$

(55)

$$ \frac{\partial M}{\partial x} - \rho I\frac{{\partial^{3} v}}{{\partial x\partial t^{2} }} - C_{\text{OD2}} \frac{{\partial^{2} v}}{\partial x\partial t} - \frac{1}{2}C_{\text{D}} \rho A\frac{\partial }{\partial x}\left( {\frac{\partial v}{\partial t}} \right)^{2} - V_{*} = 0 $$

(56)

$$ \frac{\partial M}{\partial x} - \rho I\frac{{\partial^{3} v}}{{\partial x\partial t^{2} }} - C_{\text{OD2}} \frac{{\partial^{2} v}}{\partial x\partial t} - \frac{1}{2}C_{\text{D}} \rho A\frac{\partial }{\partial x}\left( {\frac{\partial v}{\partial x}} \right)^{2} + \kappa AG\left( {\frac{\partial v}{\partial x} - \psi } \right) $$

(57)

Where the internal moment force moment

$$ M = EI\frac{{\partial^{2} v}}{{\partial x^{2} }} + \vartheta v(t)\left[ {H(x) - H(x - L)} \right] $$

(58)

The bending slope due to pure bending can be defined as

$$ \psi = \frac{\partial v}{\partial x} $$

(59)

$$ M = EI\frac{\partial \psi }{{\partial x^{2} }} + \vartheta v(t)\left[ {H(x) - H(x - L)} \right] $$

(60)

$$ \begin{aligned} \frac{\partial }{\partial x}\left[ {EI\frac{\partial \psi }{\partial x}} \right] & - \rho I\frac{{\partial^{2} \psi }}{{\partial t^{2} }} - C_{\text{OD2}} \frac{\partial \psi }{\partial t} - \frac{1}{2}C_{\text{D}} \rho A\left| {\frac{\partial \psi }{\partial t}} \right| \times \left| {\frac{\partial \psi }{\partial t}} \right| \\ & + \kappa AG\left( {\frac{\partial v}{\partial x} - \psi } \right) + \vartheta v(t)\left[ {H(x) - H(x - L)} \right] \\ \end{aligned} $$

(61)

$$ \begin{aligned} EI\frac{{\partial^{2} \psi }}{{\partial x^{2} }} & - \rho I\frac{{\partial^{2} \psi }}{{\partial t^{2} }} - C_{\text{OD2}} \frac{\partial \psi }{\partial t} - \frac{1}{2}C_{\text{D}} \rho A\left| {\frac{\partial \psi }{\partial t}} \right| \times \left| {\frac{\partial \psi }{\partial t}} \right| \\ & + \kappa AG\left( {\frac{\partial v}{\partial x} - \psi } \right) + \vartheta v(t)\left[ {H(x) - H(x - L)} \right] = 0 \\ \end{aligned} $$

(62)

$$ \begin{aligned} \left[ {EI\frac{{\partial^{2} \psi }}{{\partial x^{2} }}} \right] & - \rho I\frac{{\partial^{2} \psi }}{{\partial t^{2} }} - C_{\text{OD2}} \frac{\partial \psi }{\partial t} - \frac{1}{2}C_{\text{D}} \rho A\left| {\frac{\partial \psi }{\partial t}} \right| \times \left| {\frac{\partial \psi }{\partial t}} \right| \\ & + \kappa AG\left( {\frac{\partial v}{\partial x} - \psi } \right) + \vartheta v(t)\left[ {H(x) - H(x - L)} \right] = 0 \\ \end{aligned} $$

(63)

Where the translation equation of the equilibrium becames

$$ \hat{m}\frac{{\partial^{2} v}}{{\partial t^{2} }} + \kappa AG\left[ {\frac{\partial \psi }{\partial x} - \frac{{\partial^{2} v}}{{\partial x^{2} }}} \right] + C_{\text{OD1}} \frac{\partial v}{\partial t} + \frac{1}{2}C{}_{\text{D}}\rho A\left| {\frac{\partial v}{\partial t}} \right| \times \left| {\frac{\partial v}{\partial t}} \right| = 0 $$

(64)

where

$$ \hat{m} = \left( {\rho_{s} t_{s} + \rho_{p} t_{p} } \right)b $$

$\rho_{s}$ then of the substrate, $t_{s}$ thickness of substrate, $\rho_{p}$ density of piezeoelectric material, $t_{p}$ thickness of piezeoelectric material.