1 Introduction

Hull girder strength is the most fundamental property to secure the safety of ships. International Association of Classification Societies (IACS) has strengthened the rules for hull girder safety recently. Unified requirement (UR) [1] on hull girder strength was first introduced in 1989. Recently, Common Structural Rules for new ship construction standards (CSR) [2, 3] were developed and entered into force. In CSR, ultimate strength check has been introduced as a new criterion based on ultimate limit state design.

Many researchers have studied the ultimate strength of hull girders. The first attempt to rationally evaluate the ultimate strength of ship structure was made by Caldwell [4]. He applied rigid plastic mechanism analysis to evaluate the ultimate strength of a ship’s hull girder, and accounted for the effect of buckling by reducing the yield stress of the material at the buckled part. However, his method does not account for the post-collapse strength of the structural members which significantly influence the collapse strength. This problem was further addressed by Smith [5]. Smith proposed another simple but efficient method to analyze progressive collapse behavior of box girder structures under longitudinal bending. The progressive loss in stiffness of a cross section due to buckling and yielding of structural components was taken into account. Yao et al. [6, 7] proposed a simple and practical analytical method to simulate progressive collapse behavior of a ship’s hull subjected to longitudinal bending based on Smith’s method, so as to estimate the load carrying capacity of a ship’s hull including its post-ultimate strength behavior. In their method, progressive loss in stiffness due to the occurrence of buckling and yielding of structural components were taken into account, and the deflection mode of a stiffener not only as an Euler buckling but also a flexural–torsional buckling was considered. Recent developments may be found in Yao et al. [8].

In order to assess the safety of ship structure, evaluation of the extreme loads is another important aspect. Smith [9] measured the wave loads on destroyers, and showed nonlinear characteristics that the vertical bending moments in sagging are larger than those in hogging. Yamamoto et al. [10] treated the ship hull as a rigid body, and calculated time series of the motion and longitudinal bending moment of a tanker in head seas taking the nonlinearity into account. Then the authors regarded the ship hull as an elastic beam theoretically taking account of the dynamic amplification effect due to the elasticity [11]. Jensen and Pedersen [12] also proposed a nonlinear strip theory formulated in frequency domain based on a perturbation procedure. Later, this approach was extended to account for the hydroelasticity in time domain by Xia et al. [13].

When it is assumed that the severity of a hull girder collapse is directly related to the consequence of the collapse, clarifying how the hull girder collapses in waves, i.e., to what extent the hull girder collapses in waves, is important in evaluating the associated risk of the hull girder collapse. The risk may include the loss of ship itself, cargoes and lives, oil pollution, etc. Some of the authors have studied the target safety level of a ship’s hull girder based on risk optimization, and have shown that the target safety level is affected by the scope of risk model [14]. Then focus should be put more on the extent of the failure with the increase of interests in risk-based design. Progressive collapse behavior of a ship’s hull girder is usually analyzed in a quasi-static manner over a cross section by displacement control, i.e., by monotonously increasing curvature. However, as Lehman [15] pointed out, the input of a curvature does not adequately represent the failure process. The actual path of the progressive collapse behavior is not followed by imposing forced displacement/rotation, nor by imposing force. Instead, it can be followed only when the interaction between the collapsing structure and loads is considered (Yao et al. [16]).

Hydroelasticity is a research field in which the interaction between the fluid and structure in an elastic range is considered. Following this manner, the present problem may be called hydroelasto-plasticity. The structural deformation including plastic deformations may have a significant influence on the equilibrium between the ship’s motion and the hydrostatic/dynamic forces as the external loads which exceed the ultimate strength should be compensated by the inertia forces of the ship body in large plastic deformation. Such an analysis can be called a hydroelasto-plastic response analysis.

As far as the present authors know, Masaoka and Okada [17] developed such an analysis system for dynamic behavior of hull girders in elastic and plastic ranges, and compared the dynamic collapse behavior of a damaged ship in large regular waves with that of an intact ship. It was also shown that the post-ultimate bending strength of the hull girder is important in predicting the structural stability of the collapse. However, the results were not validated against experiments, nor was the collapse behavior clearly explained. In addition, the analysis was performed only under regular sea conditions.

In this paper, the dynamic collapse behavior in a large single wave was studied numerically and experimentally as the first step since the irregular extreme seas can be regarded as a collection of large single waves. Nonlinear strip theory is used to evaluate the hydrodynamic loads taking account of the large plastic deformations. For experimental validation, a scaled model was designed and fabricated. The scaled model consists of two rigid bodies connected amidship by a device which represents a nonlinear relation between the vertical bending moment and the rotational angle. Then a series of tank tests are conducted by using the scaled model.

2 Hydroelasto-plasticity theory

2.1 Premises

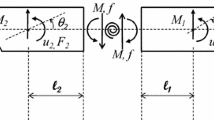
The whole ship hull is modeled as two rigid bodies connected amidship by a nonlinear rotational spring as shown in Fig. 1. The right and left bodies are called body 1 and body 2, respectively, for convenience. The rotational spring represents the nonlinear relation between the moment and the displacement, including reduction of load carrying capacity due to buckling and yielding, increase of the capacity due to material strain-hardening, and recovery of the bending rigidity when unloaded. Such a relation is exemplified in Fig. 2.

Fig. 1
figure 1

Free-body diagram for the two-rigid-bodies system

Full size image
Fig. 2
figure 2

Schematic relationship between vertical bending moment and rotational angle

Full size image

F 1 and F 2 in Fig. 2 represent the external loads on the respective bodies, and M 1 and M 2 the external moments measured around the center of gravity of the respective bodies. f and M represent the reaction force and moment due to the spring, respectively. u 1 and u 2 are the vertical displacements of two parts measured at the connection, θ 1 and θ 2 show the rotational displacement of the respective bodies.

2.2 Formulations

The internal bending moment M is a function of the relative rotational angle θ. When the structural damping which is proportional to the rate of the relative rotational angle is included, the internal bending moment can be given as,

$$ M = M\left( \theta \right) + c_{k} \dot{\theta }, $$
(1a)

or its incremental form,

$$ {{\Updelta}}M = k_{R} \Updelta \,\theta + c_{k} \Updelta \,\dot{\theta }, $$
(1b)

where, θ = θ 1 − θ 2, k R is a tangential stiffness of the function M (θ), and c k is the structural damping coefficient. The equilibrium equations of motion can be obtained by reference to their centers of gravity as,

$$ \begin{gathered} m_{11}^{1} \ddot{u}_{1} + m_{12}^{1} \ddot{\theta }_{1} + C_{11}^{1} \dot{u}_{1} + C_{12}^{1} \dot{\theta }_{1} + K_{11}^{1} u_{1} + K_{12}^{1} \theta_{1} = F_{{ 1 {\text{w}}}} + f \hfill \\ m_{11}^{2} \ddot{u}_{2} + m_{12}^{2} \ddot{\theta }_{2} + C_{11}^{2} \dot{u}_{2} + C_{12}^{2} \dot{\theta }_{2} + K_{11}^{2} u_{2} + K_{12}^{2} \theta_{2} = F_{{ 2 {\text{w}}}} - f \hfill \\ m_{21}^{1} \ddot{u}_{1} + m_{22}^{1} \ddot{\theta }_{1} + C_{21}^{1} \dot{u}_{1} + C_{22}^{1} \dot{\theta }_{1} + K_{21}^{1} u_{1} + K_{22}^{1} \theta_{1} = M_{{ 1 {\text{w}}}} - M - f\ell_{1} \hfill \\ m_{21}^{2} \ddot{u}_{2} + m_{22}^{2} \ddot{\theta }_{2} + C_{21}^{2} \dot{u}_{2} + C_{22}^{2} \dot{\theta }_{2} + K_{21}^{2} u_{2} + K_{22}^{2} \theta_{2} = M_{{ 2 {\text{w}}}} + M - f\ell_{2} \hfill \\ \end{gathered} $$
(2)

where, m ii (i, j = 1–2) represents mass and inertia including added mass and inertia, C ij represents hydrodynamic damping, while K ij represents the restoring force coefficient due to hydrostatic pressure. The superscript indicates the body 1 (aft) and 2 (fore), respectively. f is vertical shear force, F 1w and F 2w, and M 1w and M 2w are wave-induced vertical forces and bending moments, respectively. The above equations simply represent the balance among intertia, external loads and reactions by the nonlinear spring. The external loads F 1, F 2, M 1 and M 2 to the hull including the added mass and hydrodynamic damping terms, restoring forces and moments due to static pressure, and wave-induced forces and moments are evaluated by using a nonlinear strip theory. Static loads such as still-water bending moments, gravity loads and buoyancy are not included for simplicity, however, they may be easily considered in the above equation.

The compatibility condition at the midship part is given as,

$$ u_{1} - \ell_{1} \theta_{1} = u_{2} + \ell_{2} \theta_{2} $$
(3)

By eliminating u 1 and f, the equations may read in an incremental form.

$$ \begin{gathered} \left[ {\begin{array}{*{20}c} {m_{11}^{1} + m_{11}^{2} } & {m_{12}^{1} + \ell_{1} m_{11}^{1} } & {m_{12}^{2} + \ell_{2} m_{11}^{1} } \\ {m_{21}^{1} - \ell_{1} m_{11}^{2} } & {m_{22}^{1} + m_{21}^{1} \ell_{1} } & {m_{21}^{1} \ell_{2} - \ell_{1} m_{12}^{2} } \\ {m_{21}^{2} - \ell_{2} m_{11}^{2} } & 0 & {m_{22}^{2} - \ell_{2} m_{12}^{2} } \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {\Updelta \ddot{u}_{2} } \\ {\Updelta \ddot{\theta }_{1} } \\ {\Updelta \ddot{\theta }_{2} } \\ \end{array} } \right\} \hfill \\ + \left[ {\begin{array}{*{20}c} {C_{11}^{1} + C_{11}^{2} } & {C_{12}^{1} + \ell_{1} C_{11}^{1} } & {C_{12}^{2} + \ell_{2} C_{11}^{1} } \\ {C_{21}^{1} - \ell_{1} C_{11}^{2} } & {C_{22}^{1} + C_{21}^{1} \ell_{1} + c_{k} } & {C_{21}^{1} \ell_{2} - \ell_{1} C_{12}^{2} - c_{k} } \\ {C_{21}^{2} - \ell_{2} C_{11}^{2} } & { - c_{k} } & {C_{22}^{2} - \ell_{2} C_{12}^{2} + c_{k} } \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {\Updelta \dot{u}_{2} } \\ {\Updelta \dot{\theta }_{1} } \\ {\Updelta \dot{\theta }_{2} } \\ \end{array} } \right\} \hfill \\ + \left[ {\begin{array}{*{20}c} {K_{11}^{1} + K_{11}^{2} } & {K_{12}^{1} + \ell_{1} K_{11}^{1} } & {K_{12}^{2} + \ell_{2} K_{11}^{1} } \\ {K_{21}^{1} - \ell_{1} K_{11}^{2} } & {K_{22}^{1} + K_{21}^{1} \ell_{1} + k_{R} } & {K_{21}^{1} \ell_{2} - \ell_{1} K_{12}^{2} - k_{R} } \\ {K_{21}^{2} - \ell_{2} K_{11}^{2} } & { - k_{R} } & {K_{22}^{2} - \ell_{2} K_{12}^{2} + k_{R} } \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {\Updelta u_{2} } \\ {\Updelta \theta_{1} } \\ {\Updelta \theta_{2} } \\ \end{array} } \right\} \hfill \\ = \left\{ {\begin{array}{*{20}c} {F_{{ 1 {\text{w}}}} + F_{{ 2 {\text{w}}}} } \\ {M_{{ 1 {\text{w}}}} - \ell_{1} F_{{ 2 {\text{w}}}} } \\ {M_{{ 2 {\text{w}}}} - \ell_{2} F_{{ 2 {\text{w}}}} } \\ \end{array} } \right\} - \left[ {\begin{array}{*{20}c} {m_{11}^{1} + m_{11}^{2} } & {m_{12}^{1} + \ell_{1} m_{11}^{1} } & {m_{12}^{2} + \ell_{2} m_{11}^{1} } \\ {m_{21}^{1} - \ell_{1} m_{11}^{2} } & {m_{22}^{1} + m_{21}^{1} \ell_{1} } & {m_{21}^{1} \ell_{2} - \ell_{1} m_{12}^{2} } \\ {m_{21}^{2} - \ell_{2} m_{11}^{2} } & 0 & {m_{22}^{2} - \ell_{2} m_{12}^{2} } \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {\ddot{u}_{2} } \\ {\ddot{\theta }_{1} } \\ {\ddot{\theta }_{2} } \\ \end{array} } \right\} \hfill \\ - \left[ {\begin{array}{*{20}c} {C_{11}^{1} + C_{11}^{2} } & {C_{12}^{1} + \ell_{1} C_{11}^{1} } & {C_{12}^{2} + \ell_{2} C_{11}^{1} } \\ {C_{21}^{1} - \ell_{1} C_{11}^{2} } & {C_{22}^{1} + C_{21}^{1} \ell_{1} } & {C_{21}^{1} \ell_{2} - \ell_{1} C_{12}^{2} } \\ {C_{21}^{2} - \ell_{2} C_{11}^{2} } & 0 & {C_{22}^{2} - \ell_{2} C_{12}^{2} } \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {\dot{u}_{2} } \\ {\dot{\theta }_{1} } \\ {\dot{\theta }_{2} } \\ \end{array} } \right\} \hfill \\ - \left[ {\begin{array}{*{20}c} {K_{11}^{1} + K_{11}^{2} } & {K_{12}^{1} + \ell_{1} K_{11}^{1} } & {K_{12}^{2} + \ell_{2} K_{11}^{1} } \\ {K_{21}^{1} - \ell_{1} K_{11}^{2} } & {K_{22}^{1} + K_{21}^{1} \ell_{1} } & {K_{21}^{1} \ell_{2} - \ell_{1} K_{12}^{2} } \\ {K_{21}^{2} - \ell_{2} K_{11}^{2} } & 0 & {K_{22}^{2} - \ell_{2} K_{12}^{2} } \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {u_{2} } \\ {\theta_{1} } \\ {\theta_{2} } \\ \end{array} } \right\} - \left\{ {\begin{array}{*{20}c} 0 \\ M \\ { - M} \\ \end{array} } \right\} \hfill \\ \end{gathered} $$
(4)

Once the initial conditions are given, the increments can be obtained in time marching step by using a numerical integration scheme such as the Newmark β method.

2.3 External load evaluation

The external loads are evaluated by using a time-domain nonlinear method based on ordinary strip theory, which has been developed by Fujino et al. [18]. Only the motions within a vertical plane are modeled herein. A Cartesian coordinate system o-xyz is defined as a set of axes translating with the forward speed U. The origin is set at the midship. The x-axis is taken in the ship’s longitudinal direction and the z-axis is taken positive upwards with plane z = 0 representing the calm water level. Then the vertical load on a cross section per unit length f dz may be given as follows:

$$ f_{dz} = \frac{\text{d}}{{{\text{d}}t}}\left[ {m_{HH} \frac{{{\text{d}}\varsigma }}{{{\text{d}}t}}} \right] + N_{HH} \frac{{{\text{d}}\varsigma }}{{{\text{d}}t}} + \int\limits_{{C^{\prime}}} {pn_{z} dl - w} $$
(5)

where \( \frac{\text{d}}{{{\text{d}}t}} = \frac{\partial }{\partial t} - U\frac{\partial }{\partial x}, \) m HH is the added mass in vertical direction per unit length, N HH is the damping force coefficient per unit length, ς is the relative wave elevation to the vertical motion of the cross section, p is the pressure evaluated assuming the waves are undisturbed by the ship body, n z is the vertical component of the outward normal vector within the cross section and w is the weight per unit length. The vertical motion of the cross section at x = X is given for the body 1 and body 2, respectively, as follows:

$$ z_{1} = u_{1} - \left( {\ell_{1} - X} \right)\theta_{1} $$
(6a)
$$ z_{2} = u_{2} + \left( {\ell_{2} + X} \right)\theta_{2} $$
(6b)

The wave elevation η for the long-crested wave spectrum S (ω) at x = X and t = T, can be given, for example, as follow:

$$ \eta \left( {X,T} \right) = \sum\limits_{i = 1}^{n} {u_{i} \sqrt {S\left( {\omega_{i} } \right)\Updelta \omega } \cos \left( {k_{i} X + \omega_{i} T} \right)} + \bar{u}_{i} \sqrt {S\left( {\omega_{i} } \right)\Updelta \omega } \sin \left( {k_{i} X + \omega_{i} T} \right) $$
(7)

where ω i is the wave circular frequency of the i-the elementary wave, k i is the corresponding wave number, u i and \( \bar{u}{}_{i} \) are independent sets of independent zero-mean Gaussian variable with unit variance.

The integration in Eq. 5 is performed over the instantaneous wetted surface \( C^{\prime} \) of the cross section. The added mass and damping are also evaluated for the submerged part below the instantaneous wetted surface. In Eq. 5, impact loads due to the change of the added mass with respect to time are also included. However, in the present study, the effects are not accounted for to exclude the transient response after slamming impact. For the evaluation of the added mass and damping force coefficient, the so-called close-fit method [19] is employed assuming that the fluid is incompressible and irrotational, the amplitude of fluid motion is small, and the fluid action is two-dimensional within the cross section. Then the loads per unit length are integrated along x-axis to obtain the loads on the respective bodies. For the integration, the whole ship is sectioned into N strips. N = 21 is employed in this study.

The ship’s hull girder may be subjected to multiple large waves in severe irregular seas; however, dynamic collapse behavior in large single wave is pursued as a first step. The large single wave is realized by using a focused wave technique. The focused wave can be modeled by a sum of regular elementary waves as given in Eq. 7. By following Der Kiureghian [20] and Jensen et al. [21], the time series of waves which takes the maximum corresponding to the prescribed probability level can be given by employing reliability theory. Although the method in their proposal is to detect the extreme response itself, in this study, the extreme wave elevation is targeted, regarding the wave itself as a response.

When a limit state function g is defined as:

$$ g\left( {u_{1} ,\bar{u}_{1} ,u_{2} ,\bar{u}_{2} , \ldots ,u_{n} ,\bar{u}_{n} } \right) \equiv \eta_{0} - \eta \left( {\left. {x_{0} ,t_{0} } \right|u_{1} ,\bar{u}_{1} ,u_{2} ,\bar{u}_{2} , \ldots ,u_{n} ,\bar{u}_{n} } \right) $$
(8)

A problem to seek the probability of the irregular wave exceeding the threshold value η 0 at t = t 0 and x = x 0 is formulated as limit state problem. An approximate solution can be obtained by first order reliability method (FORM). A set of \( \left\{ {u_{i}^{*} ,\bar{u}_{i}^{*} } \right\} \) can be given as the design point on g = 0 minimizing the distance to the origin. The distance is defined as the reliability index β. Then the probability of wave elevation exceeding η 0 is given as p f  = Φ (−β) where \( \Upphi \left( \cdot \right) \) is the standard normal distribution function.

3 Experiment

3.1 Experimental model design

The numerical method addressed in the previous section needs to be validated by tank tests using a scaled model. A box-shape ship was selected as a generic ship for simplicity and clarity. The box ship is 300 m in length, 40 m in breadth, 30 m in depth and 10 m in draft. Its scale ratio α is chosen to be 1/100. Then the main particulars of the model are length L = 3 m, breadth B = 0.4 m, depth D = 0.3 m and draught d = 0.1 m.

The mechanical properties of the model should also be scaled according to the law of similitude. The similitude of the load characteristics may be attained by keeping similarity in geometry and following the Law of Froude. In addition, similitude of strength characteristics must be attained as well since the present focus is the collapse behavior in waves. The requirements for the scaled model from the viewpoint of strength characteristics are summarized as follows: (1) to realize the strength capacity model of the hull girder both in loading and unloading as shown in Fig. 2, (2) to collapse in waves which can be generated in the tank, (3) to be free from severe wave-induced vibrations, and (4) to be repeatable for multiple collapse tests.

The requirement (1) means that the reduction of strength in post-ultimate strength range accompanied by buckling of stiffened panels, or at least the reduction of the stiffness after the collapse moment, should be reproduced. The requirement (2) means keeping the law of similitude in ‘strength’ itself. That is, the scaled model must collapse under wave loads which are generated in the tank. The design value of the wave bending moment M w is proportional to α 4 since it is given as \( M_{\text{w}} = C\rho gBL^{2} \eta \) where η is the wave amplitude, and ρg is the specific gravity of the water. C is a coefficient which varies depending on the ship’s geometry, specifically on the block coefficient. C = 0.04 may be assumed at the design stage. The requirement (3) is raised as in the present study, dynamic amplification effects such as whipping response are excluded from the response in the tank tests. The last requirement (4) is given as the tank tests are planned to be conducted more than once.

The design methodology is detailed in Wada et al. [22]. In their research, various types of design alternatives have been investigated. The final design to meet all the above requirements is shown in Figs. 3 and 4. The two bodies are connected to each other by a hinge at deck level while a sacrificial beam specimen is fixed to the bottom of the ship’s fore body and connected to the ship’s aft body via a rigid boom. The specimen bends and bears shear force when the hull girder deforms at the hinge, subjected to the bending moment loaded over the structure. The nonlinear relationship between the moments and rotational angle is reproduced by the collapse mechanism of the specimen as it collapses due to yielding to excessive bending moments. The yielding occurs at the upper end of the specimen, as the bending moment is the largest at the root of the specimen. A circular pillar specimen with diameter 10 mm cut out from a block of steel SS400 is used. The collapse tests can be conducted more than once by changing the sacrificial specimens.

Fig. 3
figure 3

Sketch of the experimental model. Two rigid bodies are connected by a hinge. The specimen bears shear force under hull girder bending moment

Full size image
Fig. 4
figure 4

Photo zoom-up of the midship. The part surrounded by broken lines shows the specimen

Full size image

Prior to the tank tests, static four-point-bending tests were conducted to detect the load carrying capacity of the specimen. It was found that the collapsing moment of the hull girder is 18 GNm in real scale (Fig. 5). The vertical axis shows the vertical bending moment over the hull girder in sagging. Repeatability of the tests could also be confirmed. The capacity reduction after the ultimate strength was not realized in the present specimens since only yielding occurs in the specimen whereas the capacity reduction is accompanied by buckling. In the figure, FE-results in which solid elements are employed and the material is assumed to be elasto-perfectly plastic are also presented. The discrepancies may be attributed to the strain hardening effects.

Fig. 5
figure 5

Moment-rotational angle relationship measured in the static tests

Full size image

3.2 Tank test

A series of tank tests was conducted in the towing tank, Osaka University. The tank is 100 m in length, 7.8 m in breadth, and 4.30 m in depth and has the plunger wave maker. As explained, a focused wave technique was employed to realize a large single wave for dynamic collapse tests. First, calibrations of regular and irregular waves were conducted to obtain the transfer functions between input voltage to the wave maker and the wave elevation at the center of the tank. The target focused wave was generated from ISSC wave spectrum with the significant wave height H S of 20.0 cm (20.0 m) and with mean wave period of T 0 1.39 s (13.9 s). The significant wave height seems unrealistic; however, the hull girder does not collapse in more realistic waves. The values in the parenthesis show the values in real scale. The reliability index β = 4 (p f  = 3.2 × 10−5) was selected as it would give close estimate of the expected value of the maximum in 1000 sample peaks when the irregular waves are Gaussian distributed and narrow-banded. The focused wave was intended to occur with its negative peak around the midship part of the model at t = 80 s so that it would induce maximum sagging moment amidship.

Then the ship model was installed at the center of the tank, or 50 m away from the wave maker. No forward speed was given. Three load cells were equipped within a cross section amidship to measure the hull girder bending moments working on the cross section excluding the contribution from axial loads. A potentiometer was equipped to the model to detect the relative rotational angle between the two bodies. Four acceleration transducers were mounted along the model to measure the vertical and rotational accelerations of the respective bodies. Two wave probes were installed in the tank, one in front of the wave maker and the other at the center of the tank. All these data were sampled simultaneously at frequency 50 Hz, and transferred to PC.

Ballasts were loaded so that the target draft and target still-water bending moment in sagging were attained simultaneously. The total ballasts amounted to 588 N. Four small ballasts each weighing 49 N were placed around the midship parts and two heavier ballasts weighing each 98 N were placed at the respective centers of the two bodies. The still-water bending moment in sagging was measured to be 9.0 GNm in real scale. The still-water bending moment was subtracted from the measurement of the bending moments hereafter.

As a preliminary check, the natural frequency of the model was measured by a hammering test. When the ballasts were loaded, the natural frequency was found to be 6.88 Hz (43.2 rad/s), or 0.69 Hz (4.32 rad/s) in real scale. The natural frequency was confirmed to be out of the wave frequency range from 0.2 to 1.5 rad/s in real scale. The critical damping ratio γ was also detected to be 1.8%. Then dynamic behaviors of the scaled model were measured in regular waves with small wave amplitude to obtain transfer functions of the vertical bending moment amidship.

Finally, the collapse tests were conducted in the focused wave. A time history of the focused wave measured in the tank test is shown as a broken line in Fig. 6. The maximum wave elevation in this wave train is 0.2 (m) in model scale. The solid line in the same figure designated as numerical shows a time history of the target. The discrepancy is small around the largest peak.

Fig. 6
figure 6

Time history of wave elevation measured in the tank test. The broken line represents the measurement while the solid line represents the target time history. Data are shown in real scale

Full size image

4 Comparison and validation

4.1 Calculation condition

From the static tests, the collapsing moment, the slopes (bending rigidity) before and after the collapse were estimated to be M U = 9.2 GNm, k R  = 5.4 × 103 GNm/rad and S = 0.21 × 103 GNm/rad, respectively, in real scale. As the material of the specimen does not have explicit yielding point, the strength increases slightly due to strain hardening with the reduced slope. These values are employed in the numerical calculations. The bending rigidity recovers to k R  = 5.4 × 103 GNm/rad, again when unloading starts. These are summarized in Table 1. The wave conditions for the simulation are also summarized in the same table. The forward speed is assumed to be zero.

Table 1 Calculation conditions
Full size table

It has been found from the comparison of transfer functions that the nonlinear strip theory tends to overestimate the vertical bending moment amidship. Then a correction factor found from the comparison is multiplied to the vertical bending moment evaluated by the strip theory.

4.2 Validation

Time histories of the vertical bending moment amidship obtained by the numerical analysis and measurement in the tank test are compared in Fig. 7. Time histories of the rotational angles are also compared in Fig. 8, with vertical axis positive in sagging moments. The relationships between the moment and the rotational angle are presented in Fig. 9.

Fig. 7
figure 7

Time histories of the vertical bending moment at midship. The still-water bending moment 9.0 GNm is subtracted from the bending moment in the figure

Full size image
Fig. 8
figure 8

Time histories of the rotational angle between the two bodies

Full size image
Fig. 9
figure 9

Relationship between moment and rotational angle

Full size image

From Fig. 7, it is observed that the bending moment reaches the collapsing moment slightly before t = 80 s. Then it continues to rise with the advancement of the time, following the path BC shown in Fig. 9, with smaller positive rigidity. It is considered that the excess of the wave-induced moment over the collapsing moment is compensated by the moments induced by the rotational accelerations of the bodies as well as the capacity increase. Then the accelerations become larger and plastic deformations grow. At around t = 82 s, the structure starts to be unloaded. This implies that the duration of collapse lasts only a few seconds. Then, at around t = 87 s, the bending moment takes the maximum negative value. According to Fig. 8, the rotational angle changes within a short duration at around t = 80 s in the order 0.012 rad. This indicates that the hull girder collapses rapidly after reaching collapsing moment. This can also be illustrated in Fig. 9, which shows the relationship between the bending moment and rotational angle amidship. After unloading starts at point C, the rotational deformation does not change largely due to the recovery of the large rigidity along the path CD.

The slowly varying oscillation after point C in Fig. 9 is excited by the remaining external force after the largest peak of the focused wave packet passes along the ship. In addition, among the oscillation, even higher frequency oscillation around 0.7 Hz is recognized in the numerical results. They are considered to be transient vibrations. When the damping effect of spring was neglected, the higher frequency components become more prominent while the vibration almost disappears when the structural damping is included.

5 Discussions

5.1 Parameters affecting the severity

There are various factors that may affect the severity of hull girder collapse behavior, or to what extent the ship collapses in waves. The severity of collapse is defined herein as the plastic deformation as shown in Fig. 8. It would be easily imagined that the severity of collapse is dependent on the external load. The severity would be larger in larger waves. The strength capacity characteristics may also affect the severity. In Table 2, the parameters which may affect the severity are summarized. The relationship between bending moment capacity and the relative rotational angle is simplified as in Fig. 10. The drop of capacity after the ultimate strength is most rapid just after the ultimate strength, however, it becomes relatively moderate corresponding to the post-ultimate capacity of the buckled members at the compression side of hull girder bending [6, 7]. This behavior is approximately taken into account by introducing a final constant capacity of M BC. Other calculation conditions are identical to those in Table 1 unless otherwise mentioned.

Table 2 Summary of parametric studies
Full size table
Fig. 10
figure 10

A simplified model for relationships between vertical bending moment and rotational angle

Full size image

5.2 Capacity model

5.2.1 Rigidity

Collapse behaviors for three different rigidities after the collapsing moment, or ultimate strength, are calculated and compared. The significant wave height is 18.5 m in these cases. First, in case (1-a), the rigidity after the ultimate strength decreases but the value is still positive. In the second case (1-b), the rigidity is equal to zero after the ultimate strength. In the third case (1-c), the rigidity takes a negative value and the load carrying capacity decreases. Time histories of relative rotational angle between the two bodies are shown in Fig. 11. The severity is the largest for case (1-c). In this case, plastic deformation increases very rapidly and unstably after the ultimate strength is reached. Thus, the rigidity of the path after the ultimate strength may largely affect the extent of collapse.

Fig. 11
figure 11

Time histories of relative rotational angle between the two bodies (case 1). The parameter is the rigidity after the collapsing moment is reached

Full size image

5.2.2 Capacity drop

Capacity drop is defined as the difference between the ultimate strength M U and the final constant capacity moment M BC in Fig. 10. Figure 12 shows time series of relative rotational angle between the two bodies when the capacity drop is varied. The values of M BC are 9.17, 7.33, 5.50, and 3.60 (GNm), respectively. When the capacity drop factor β defined as:

Fig. 12
figure 12

Time series of relative rotational angle between the two bodies (case 2). The capacity drop factor is varied

Full size image
$$ \beta = \frac{{M_{\text{U}} - M_{\text{BC}} }}{{M_{\text{U}} }} $$

The capacity drop factors β corresponding to the above M BC values are 0.0, 0.2, 0.4, and 0.6, respectively. Figure 13 compares the relationship between the capacity drop factor β and the severity of collapse. In this figure, the results for β = 0.1, 0.3, 0.5, 0.7, and 0.9 are also plotted. It is interesting that the severity increases linearly with the capacity drop factor.

Fig. 13
figure 13

The relationship between the severity of collapse and the capacity drop factor β defined as \( {{\left( {M_{\text{U}} - M_{\text{BC}} } \right)} \mathord{\left/ {\vphantom {{\left( {M_{\text{U}} - M_{\text{BC}} } \right)} {M_{\text{U}} }}} \right. \kern-\nulldelimiterspace} {M_{\text{U}} }} \) (case 2). The same wave condition with significant wave height 16.9 m and with mean period 13.9 s is employed

Full size image

5.2.3 Structural damping

In Fig. 8, time histories of relative rotational angle between the two bodies for cases with/without structural damping are plotted. When attention is paid to the severity of collapse, it turns out that it is smaller when the structural damping is considered. Further results are found in Fig. 14 presented in the next section. The mechanism may be partly explained by using the principle of energy conservation. It is considered that the energy absorbed by the structure decreases with the decrease of plastic deformation. It could be hypothesized that the decrease of the energy absorption by the structure should be compensated by the energy dissipation increase due to the larger structural damping if the external work on the structural system done by the wave is constant. It is further discussed partly in the next section.

Fig. 14
figure 14

Relationship between the severity of collapse and the maximum amplitude of the focused wave (case 4). The wave period is fixed at 13.9 s. Solid boxes represent the result without structural damping while triangles the result with structural damping (case 3)

Full size image

5.3 Load model

5.3.1 Wave amplitude

The significant wave height is varied from 16.9 to 23.1 m. As large single waves are generated by using the focused wave technique for the reliability level β = 4, then the maximum amplitude of the focused wave is almost equal to the significant wave height. In Fig. 14, open triangles show the relationship between the severity of collapse and the wave amplitude. The severity is close to zero when the wave amplitude is 16.9 m at which the collapsing moment is almost equal to the maximum internal load induced by the wave load. It is observed that the severity of collapse increases in proportion to the wave height.

In the same figure, solid boxes show the results when the structural damping is neglected. It is observed that the severity also increases linearly with the increase of wave amplitude in these results, and that the severity for cases with structural damping is always smaller than that without structural damping given the same wave amplitude. The difference between them is approximately 25%. It is expected that the difference becomes larger when the structural damping is increased.

5.3.2 Wave period

The extreme vertical bending moment may be attained in the most severe short-term sea states during the ship’s life as discussed by Kawabe et al. [23]. It may be assumed that the mean period of the most severe short-term sea states ranges from 10 to 20 s. With these in mind, the mean wave periods of 10.0, 13.9, 18.9 and 23.9 s are considered herein.

It should also be considered that the amplitude of wave loads per unit wave amplitude varies according to the period of the incident waves as well as the heading angle which the ship may be subject to. In order to exclude the effects of the difference in the amplitude of the wave loads, the wave amplitude is adjusted so that the maximum of the vertical bending moment, or the internal load becomes constant among the four cases. It is performed as follows. Firstly, the vertical bending moments are calculated for waves with the respective mean wave periods and with significant wave height 18.5 m assuming that the ship does not collapse (collapsing moment is set as infinity). Then the significant wave height that gives the same maximum value of the internal loads as that for the case (5-b) is estimated, and confirmed again by the simulation. Finally, the significant wave height is selected as 23.7, 18.5, 25.8, and 36.3 m for the respective cases of wave periods.

Figure 15 summarizes the relationship between the severity of collapse and the mean wave period. There is a clear tendency that the severity is smaller for the shorter mean wave period. It seems that the collapse grows depending on the length of the collapse duration, or time duration from the instance when the vertical bending moment reaches the ultimate strength, to the instance when unloading starts.

Fig. 15
figure 15

Relationship between the severity of collapse and the mean wave period (case 5). For each mean wave period, the significant wave height is adjusted to achieve the same maximum bending moment

Full size image

Another possible source of the extreme vertical bending moment is slamming-induced whipping response. Then the extreme vertical bending moment rapidly increases and vanishes within 1 s. Although in the present simulations, the impact load model is not implemented, the above results also indicate that the severity of collapse would be much smaller under impact loads with short time duration.

6 Conclusions

In this study, a hydroelasto-plasticity approach to predicting the dynamic collapse behavior of a ship’s hull girder in waves has been proposed. Focus is placed on the post-ultimate strength behavior, or to what extent ship may collapse in a large wave in terms of plastic deformation. A numerical simulation method has been validated against the tank tests using a newly developed scaled model. Then a series of parametric studies has been conducted by using the numerical simulation. The following conclusions are derived.

  • The fundamental dynamic collapse behavior can be followed by the proposed method. This approach can effectively predict the bending collapse behavior of a ship’s hull girder in waves.

  • The hull girder collapses rapidly after the ultimate strength is reached. The ship collapse is terminated when unloading starts at the collapsed section and the bending rigidity recovers.

  • The severity of collapse of ship’s hull girder in a large single wave depends both on its strength capacity and load models.

  • The drop of capacity after the ultimate strength plays an important role in predicting the severity of collapse.

  • Given the same amplitude bending moment, waves of shorter wave period result in the smaller severity of collapse.

The last item implies that the hull girder may not collapse largely under whipping loads. It could be rationalized that whipping loads are not considered for checking the hull safety in the current design practice.

In the future work, parametric dependencies of the severity of collapse must be clarified in a more rational manner. It is currently underway by a part of the present authors [24, 25]. The severity of successive collapse in irregular seas must be clarified both in deterministic and probabilistic aspects. As regards to the tank tests, a specimen to reproduce the reduction of the load carrying capacity after reaching the ultimate strength must be developed and implemented in the tank tests.