Nonlinear vibration analysis of smart truncated conical porous composite shells reinforced with Terfenol-D particles

Abstract

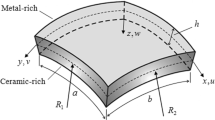
This article analyzes the nonlinear vibrations of porous truncated conical polyvinylidene fluoride (PVDF) reinforced with Terfenol-D particles. The effective properties of the magneto-electro-elastic composite have been obtained using the Eshelby–Mori–Tanaka model. Also, the porosity in the composite is considered uniform. The governing equation of the system is derived based on the von Karman theory of nonlinear strains and the theory of first-order shear deformation by applying the principle of minimum energy potential and Hamilton's principle. These equations are solved using the generalized differential quadrature method. The effect of porosity, vertex angle, shell length, boundary conditions, and volume fraction of Terfenol-D will be discussed. Also, for validation, the obtained results were compared with those found in the literature, which was a good answer, along with the accuracy. Results show that the nonlinear to linear natural frequency ratio has a decreasing trend at the lower vertex angle. The present findings can serve as a reference point for subsequent assessments.

Appendices

Appendix A

Relations related to the calculation of the Eshelby tensor:

$$ \begin{aligned}{\overline{\text{G}}}_{1111} &= \frac{{\uppi }}{2}\mathop \int \limits_{0}^{1} {\text{A}}^{ - 1} \left( {1 - {\text{x}}^{2} } \right)\left\{ \left( {3{\text{a}}_{11} + {\text{b}}_{11} } \right)\left( {1 - {\text{x}}^{2} } \right)^{3} + \left( {4{\text{d}}_{11} + 4{\text{f}}_{11} + {\text{h}}_{11} } \right)\left( {1 - {\text{x}}^{2} } \right)^{2} {\uprho }^{2} {\text{x}}^{2} \right.\\ &\quad\quad\quad\qquad\qquad\qquad\qquad\quad\left. + \left( {4{\text{k}}_{11} + 4{\text{m}}_{11} + {\text{n}}_{11} } \right)\left( {1 - {\text{x}}^{2} } \right){\uprho }^{4} {\text{x}}^{4} + 4{\text{r}}_{11} {\uprho }^{6} {\text{x}}^{6} \right\}dx \end{aligned}$$

$$\begin{aligned} {\overline{\text{G}}}_{1122} &= \frac{{\uppi }}{2}\mathop \int \limits_{0}^{1} {\text{A}}^{ - 1} \left( {1 - {\text{x}}^{2} } \right)\Bigg\{ \left( {{\text{a}}_{11} + 3{\text{b}}_{11} } \right)\left( {1 - {\text{x}}^{2} } \right)^{3} + \left( {4{\text{d}}_{11} + {\text{f}}_{11} + 3{\text{h}}_{11} } \right)\left( {1 - {\text{x}}^{2} } \right)^{2} {\uprho }^{2} {\text{x}}^{2} \\ &\quad\quad\quad\quad\qquad\qquad\qquad\quad\quad + \left( {4{\text{k}}_{11} + {\text{m}}_{11} + 3{\text{n}}_{11} } \right)\left( {1 - {\text{x}}^{2} } \right){\uprho }^{4} {\text{x}}^{4} + 4{\text{r}}_{11} {\uprho }^{6} {\text{x}}^{6} \Bigg\}dx \end{aligned}$$

$$\begin{aligned} {\overline{\text{G}}}_{1133} &= 2{\uppi }\mathop \int \limits_{0}^{1} {\text{A}}^{ - 1} {\uprho }^{2} {\text{x}}^{2} \Bigg\{ \left( {{\text{a}}_{11} + {\text{b}}_{11} } \right)\left( {1 - {\text{x}}^{2} } \right)^{3} + \left( {2{\text{d}}_{11} + {\text{f}}_{11} + {\text{h}}_{11} } \right)\left( {1 - {\text{x}}^{2} } \right)^{2} {\uprho }^{2} {\text{x}}^{2}\\ &\qquad\qquad\qquad\qquad\qquad\qquad + \left( {2{\text{k}}_{11} + {\text{m}}_{11} + {\text{n}}_{11} } \right)\left( {1 - {\text{x}}^{2} } \right){\uprho }^{4} {\text{x}}^{4} + 2{\text{r}}_{11} {\uprho }^{6} {\text{x}}^{2} \Bigg\}dx \end{aligned}$$

$$ {\overline{\text{G}}}_{1212} = {\overline{\text{G}}}_{2112} = {\overline{\text{G}}}_{2121} = {\overline{\text{G}}}_{1221} = \frac{\pi }{2}\mathop \int \limits_{0}^{1} {\text{A}}^{ - 1} \left( {1 - {\text{x}}^{2} } \right)^{2} \left\{ {{\text{a}}_{12} \left( {1 - {\text{x}}^{2} } \right)^{2} + {\text{b}}_{12} \left( {1 - {\text{x}}^{2} } \right){\uprho }^{2} {\text{x}}^{2} + {\text{d}}_{12} {\uprho }^{4} {\text{x}}^{4} } \right\}dx $$

$$ {\overline{\text{G}}}_{1313} = {\overline{\text{G}}}_{3113} = {\overline{\text{G}}}_{3131} = {\overline{\text{G}}}_{1331} = {\overline{\text{G}}}_{2323} = {\overline{\text{G}}}_{3223} = {\overline{\text{G}}}_{3232} = {\overline{\text{G}}}_{2332} = 2\pi \mathop \int \limits_{0}^{1} B^{ - 1} (1 - {\text{x}}^{2} ){{ \rho }}^{2} {\text{x}}^{2} \left\{ {{\text{d}}_{13} \left( {1 - {\text{x}}^{2} } \right) + {\text{f}}_{13} {\uprho }^{2} {\text{x}}^{2} } \right\}{\text{dx}} $$

$$ {\overline{\text{G}}}_{1413} = {\overline{\text{G}}}_{4113} = {\overline{\text{G}}}_{4131} = {\overline{\text{G}}}_{1431} = {\overline{\text{G}}}_{2423} = {\overline{\text{G}}}_{4223} = {\overline{\text{G}}}_{4232} = {\overline{\text{G}}}_{2432} = 2\pi \mathop \int \limits_{0}^{1} B^{ - 1} \left( {1 - x^{2} } \right)\rho^{2} x^{2} \left\{ {d_{14} \left( {1 - x^{2} } \right) + f_{14} \rho^{2} x^{2} } \right\}dx $$

$$ {\overline{\text{G}}}_{2211} = {\overline{\text{G}}}_{1122} $$

$$ {\overline{\text{G}}}_{2222} = {\overline{\text{G}}}_{1111} $$

$$ {\overline{\text{G}}}_{2233} = {\overline{\text{G}}}_{1133} $$

$$ {\overline{\text{G}}}_{3311} = {\overline{\text{G}}}_{3322} = 2\pi \mathop \int \limits_{0}^{1} B^{ - 1} \left( {1 - x^{2} } \right)\left\{ {\left( {1 - x^{2} } \right)^{2} + f_{33} \left( {1 - x^{2} } \right)\rho^{2} x^{2} + h_{33} \rho^{4} x^{4} } \right\}dx $$

$$ {\overline{\text{G}}}_{3333} = 4{\uppi }\mathop \int \limits_{0}^{1} {\text{B}}^{ - 1} {\uprho }^{2} {\text{x}}^{2} \left\{ {{\text{d}}_{33} \left( {1 - x^{2} } \right)^{2} + {\text{f}}_{33} \left( {1 - x^{2} } \right){\uprho }^{2} {\text{x}}^{2} + {\text{h}}_{33} {\uprho }^{4} {\text{x}}^{4} } \right\}{\text{dx}} $$

$$ {\overline{\text{G}}}_{3411} = {\overline{\text{G}}}_{4311} = {\overline{\text{G}}}_{3422} = {\overline{\text{G}}}_{4322} = 2\pi \mathop \int \limits_{0}^{1} {\text{B}}^{ - 1} \left( {1 - x^{2} } \right)\left\{ {{\text{d}}_{34} \left( {1 - x^{2} } \right)^{2} + {\text{f}}_{34} \left( {1 - x^{2} } \right){\uprho }^{2} {\text{x}}^{2} + {\text{h}}_{34} {\uprho }^{4} {\text{x}}^{4} } \right\}dx $$

$$ {\overline{\text{G}}}_{3433} = {\overline{\text{G}}}_{4333} = 4\pi \mathop \int \limits_{0}^{1} {\text{B}}^{ - 1} x^{2} \left\{ {{\text{d}}_{34} \left( {1 - x^{2} } \right)^{2} + {\text{f}}_{34} \left( {1 - x^{2} } \right){\uprho }^{2} {\text{x}}^{2} + {\text{h}}_{34} {\uprho }^{4} {\text{x}}^{4} } \right\}dx $$

$$ {\overline{\text{G}}}_{4411} = {\overline{\text{G}}}_{4422} = 2\pi \mathop \int \limits_{0}^{1} {\text{B}}^{ - 1} (1 - x^{2} )\left\{ {{\text{d}}_{44} \left( {1 - x^{2} } \right)^{2} + {\text{f}}_{44} \left( {1 - x^{2} } \right){\uprho }^{2} {\text{x}}^{2} + {\text{h}}_{44} {\uprho }^{4} {\text{x}}^{4} } \right\}dx $$

$$ {\overline{\text{G}}}_{4411} = 4\pi \mathop \int \limits_{0}^{1} {\text{B}}^{ - 1} {\uprho }^{2} {\text{x}}^{2} \left\{ {{\text{d}}_{44} \left( {1 - x^{2} } \right)^{2} + {\text{f}}_{44} \left( {1 - x^{2} } \right){\uprho }^{2} {\text{x}}^{2} + {\text{h}}_{44} {\uprho }^{4} {\text{x}}^{4} } \right\}dx $$

$$ A = \left\{ {a_{0} (1 - x^{2} ) + b_{0} \rho^{2} x^{2} } \right\}B $$

$$ B = d_{0} (1 - x^{2} )^{3} + f_{0} (1 - x^{2} )^{2} \rho^{2} x^{2} + h_{0} (1 - x^{2} )\rho^{4} x^{4} + k_{0} \rho^{6} x^{6} $$

$$ a_{0} = \frac{{\left( {c_{11} - c_{12} } \right)}}{2}, \quad b_{0} = c_{44} , \quad d_{0} = - c_{11} \left( {e_{15}^{2} + \kappa_{11} c_{44} } \right) $$

$$ f_{0} = - c_{44} \left\{ {e_{15}^{2} + \kappa_{11} c_{44} + \kappa_{33} c_{11} + \left( {e_{31} + e_{15} } \right)^{2} } \right\} + 2\left( {c_{13} + c_{44} } \right)\left( {e_{31} + e_{15} } \right)e_{15} - 2c_{11} e_{15} e_{33} - \kappa_{11} c_{11} c_{33} + \kappa_{11} \left( {c_{13} + c_{44} } \right)^{2} $$

$$ h_{0} = - c_{44} \left( {\kappa_{33} c_{44} + 2e_{15} e_{33} + \kappa_{11} c_{33} } \right) - c_{33} \left\{ {\kappa_{33} c_{11} + \left( {e_{31} + e_{15} } \right)^{2} } \right\} + \left( {c_{13} + c_{44} } \right)\left\{ {\kappa_{33} \left( {c_{13} + c_{44} } \right) + 2e_{33} \left( {e_{13} + e_{15} } \right)} \right\} - c_{11} e_{33}^{2} $$

$$ k_{0} = - c_{44} \left( {\kappa_{13} c_{33} + e_{33}^{2} } \right) $$

$$ a_{11} = \frac{{ - \left( {c_{11} - c_{12} } \right)\left( {e_{15}^{2} + c_{44} \kappa_{11} } \right)}}{2} $$

$$ b_{11} = - c_{11} \left( {e_{15}^{2} + c_{44} \kappa_{11} } \right) $$

$$ d_{11} = - c_{44} \left( {e_{15}^{2} + c_{44} \kappa_{11} } \right) $$

$$ f_{11} = \frac{{ - \left( {c_{11} - c_{12} } \right)\left( {c_{44} \kappa_{33} + 2e_{15} e_{33} + c_{33} \kappa_{11} } \right)}}{2} $$

$$ h_{11} = - c_{11} c_{44} \kappa_{33} - c_{44} \left( {e_{31} + e_{15} } \right)^{2} + 2\left( {c_{13} + c_{44} } \right)\left( {e_{31} + e_{15} } \right)e_{15} - 2c_{11} e_{15} e_{33} - c_{11} c_{33} \kappa_{11} + \left( {c_{13} + c_{44} } \right)^{2} \kappa_{11} $$

$$ k_{11} = - c_{44} \left( {\kappa_{33} c_{44} + 2e_{15} e_{33} + c_{33} \kappa_{11} } \right) $$

$$ m_{11} = \frac{{ - \left( {c_{11} - c_{12} } \right)\left( {c_{33} \kappa_{33} + e_{33}^{2} } \right)}}{2} $$

$$ n_{11} = - \kappa_{33} c_{11} c_{33} + \kappa_{33} \left( {c_{13} + c_{44} } \right)^{2} - c_{33} \left( {e_{31} + e_{15} } \right)^{2} - c_{11} e_{33}^{2} + 2\left( {c_{13} + c_{44} } \right)\left( {e_{31} + e_{15} } \right)e_{33} $$

$$ r_{11} = - c_{44} \left( {\kappa_{33} c_{33} + e_{33}^{2} } \right) $$

$$ a_{12} = \frac{{\left( {c_{11} + c_{12} } \right)\left( {e_{15}^{2} + \kappa_{11} c_{44} } \right)}}{2} $$

$$ b_{12} = c_{44} \left\{ {\kappa_{33} c_{11} - \frac{{\kappa_{33} \left( {c_{11} - c_{12} } \right)}}{2} + \left( {e_{31} + e_{15} } \right)^{2} - } \right\} - e_{15} \left\{ {2\left( {c_{13} + c_{44} } \right)\left( {e_{31} + e_{15} } \right) - 2c_{11} e_{33} + \left( {c_{11} - c_{12} } \right)e_{33} } \right\} + \kappa_{11} \left\{ {c_{11} c_{33} - \left( {c_{13} + c_{44} } \right)^{2} - \frac{{c_{33} \left( {c_{11} - c_{12} } \right)}}{2}} \right\} $$

$$ d_{12} = \kappa_{33} \left\{ {2\left( {c_{13} + c_{44} } \right)^{2} + \frac{{c_{33} \left( {c_{11} + c_{12} } \right)}}{2}} \right\} + c_{33} \left( {e_{31} + e_{15} } \right)^{2} - 2\left( {c_{31} + c_{44} } \right)\left( {e_{31} + e_{15} } \right)e_{33} + \frac{{e_{33}^{2} \left( {c_{11} + c_{12} } \right)}}{2} $$

$$ a_{13} = \frac{{\left( {c_{11} - c_{12} } \right)}}{2} $$

$$ b_{13} = c_{44} $$

$$ d_{13} = e_{15} \left( {e_{31} + e_{15} } \right) + \kappa_{11} \left( {c_{13} + c_{44} } \right) $$

$$ f_{14} = - c_{33} \left( {e_{31} + e_{15} } \right) + e_{33} \left( {c_{13} + c_{44} } \right) $$

$$ a_{22} = - c_{11} \left( {e_{15}^{2} + c_{44} \kappa_{11} } \right) $$

$$ b_{22} = \frac{{ - \left( {c_{11} - c_{12} } \right)\left( {e_{15}^{2} + c_{44} \kappa_{11} } \right)}}{2} $$

$$ d_{22} = - c_{44} \left( {e_{15}^{2} + c_{44} \kappa_{11} } \right) $$

$$ f_{22} = - c_{11} c_{44} \kappa_{33} - c_{44} \left( {e_{31} + e_{15} } \right)^{2} + 2\left( {c_{13} + c_{44} } \right)\left( {e_{31} + e_{15} } \right)e_{15} - 2c_{11} e_{15} e_{33} - c_{11} c_{33} \kappa_{11} + \left( {c_{13} + c_{44} } \right)^{2} \kappa_{11} $$

$$ h_{22} = - \frac{{ - \left( {c_{11} - c_{12} } \right)\left( {c_{44} \kappa_{33} + 2e_{15} e_{33} + c_{33} \kappa_{11} } \right)}}{2} $$

$$ k_{22} = - c_{44} \left( {\kappa_{33} c_{44} + 2e_{15} e_{33} + c_{33} \kappa_{11} } \right) $$

$$ m_{22} = - \kappa_{33} c_{11} c_{33} + \kappa_{33} \left( {c_{13} + c_{44} } \right)^{2} - c_{33} \left( {e_{31} + e_{15} } \right)^{2} + 2\left( {c_{13} + c_{44} } \right)\left( {e_{31} + e_{15} } \right)e_{33} - c_{11} e_{33}^{2} $$

$$ n_{22} = \frac{{ - \left( {c_{11} - c_{12} } \right)\left( {c_{33} \kappa_{33} + e_{33}^{2} } \right)}}{2} $$

$$ r_{22} = - c_{44} \left( {\kappa_{33} c_{33} + e_{33}^{2} } \right) $$

$$ a_{23} = \frac{{\left( {c_{11} - c_{12} } \right)}}{2} $$

$$ b_{23} = c_{44} $$

$$ d_{23} = e_{15} \left( {e_{31} + e_{15} } \right) + \kappa_{11} \left( {c_{13} + c_{44} } \right) $$

$$ f_{23} = e_{33} \left( {e_{31} + e_{15} } \right) + \kappa_{33} \left( {c_{13} + c_{44} } \right) $$

$$ a_{24} = \frac{{\left( {c_{11} - c_{12} } \right)}}{2} $$

$$ b_{24} = c_{44} $$

$$ d_{24} = c_{13} e_{15} - c_{44} e_{31} $$

$$ f_{24} = - c_{33} \left( {e_{31} + e_{15} } \right) + e_{33} \left( {c_{13} + c_{44} } \right) $$

$$ a_{33} = \frac{{\left( {c_{11} - c_{12} } \right)}}{2} $$

$$ b_{33} = c_{44} $$

$$ d_{33} = - \kappa_{11} c_{11} $$

$$ f_{33} = - \kappa_{11} c_{44} - \kappa_{33} c_{11} - \left( {e_{31} + e_{15} } \right)^{2} $$

$$ h_{33} = - \kappa_{33} c_{44} $$

$$ a_{34} = \frac{{\left( {c_{11} - c_{12} } \right)}}{2} $$

$$ b_{34} = c_{44} $$

$$ d_{34} = - e_{15} c_{11} $$

$$ f_{34} = - e_{15} c_{44} - e_{33} c_{11} + \left( {e_{31} + e_{15} } \right)\left( {c_{13} + c_{44} } \right) $$

$$ h_{34} = - e_{33} c_{4} $$

$$ a_{44} = \frac{{\left( {c_{11} - c_{12} } \right)}}{2} $$

$$ b_{44} = c_{44} $$

$$ d_{44} = c_{11} c_{44} $$

$$ f_{44} = c_{44}^{2} + c_{11} c_{33} - \left( {c_{13} + c_{44} } \right)^{2} $$

$$ h_{44} = c_{33} c_{44} $$

$$ S_{1111} = \frac{1}{4\pi }\left\{ {C_{11} \overline{G}_{1111} + C_{12} \overline{G}_{1221} + C_{13} \overline{G}_{1331} + e_{31} \overline{G}_{1431} } \right\} $$

$$ S_{1122} = \frac{1}{4\pi }\left\{ {C_{12} \overline{G}_{1111} + C_{11} \overline{G}_{1221} + C_{13} \overline{G}_{1331} + e_{31} \overline{G}_{1431} } \right\} $$

$$ S_{1133} = \frac{1}{4\pi }\left\{ {C_{13} \overline{G}_{1111} + C_{13} \overline{G}_{1221} + C_{33} \overline{G}_{1331} + e_{33} \overline{G}_{1431} } \right\} $$

$$ S_{1143} = \frac{1}{4\pi }\left\{ {e_{31} \overline{G}_{1111} + e_{31} \overline{G}_{1221} + e_{33} \overline{G}_{1331} + \kappa_{33} \overline{G}_{1431} } \right\} $$

$$ \begin{aligned} S_{1143} & = S_{1143} = S_{1143} = S_{1143} \\ & = \frac{1}{8\pi }\left\{ {C_{66} \left( {\overline{G}_{1212} + \overline{G}_{2211} } \right) + C_{66} \left( {\overline{G}_{1122} + \overline{G}_{2121} } \right)} \right\} \\ \end{aligned} $$

$$ \begin{aligned} S_{1313} & = S_{1331} = S_{3113} = S_{3131} \\ & = \frac{1}{8\pi }\left\{ {C_{44} \left( {\overline{G}_{1313} + \overline{G}_{3311} } \right) + e_{15} \left( {\overline{G}_{1413} + \overline{G}_{3411} } \right) + C_{44} \left( {\overline{G}_{1133} + \overline{G}_{3131} } \right)} \right\} \\ \end{aligned} $$

$$ \begin{aligned} S_{1341} & = S_{3141} \\ & = \frac{1}{8\pi }\left\{ {e_{15} \left( {\overline{G}_{1313} + \overline{G}_{3311} } \right) - \kappa_{11} \left( {\overline{G}_{1413} + \overline{G}_{3411} } \right) + e_{15} \left( {\overline{G}_{1133} + \overline{G}_{3131} } \right)} \right\} \\ \end{aligned} $$

$$ S_{2211} = \frac{1}{4\pi }\left\{ {C_{11} \overline{G}_{2112} + C_{12} \overline{G}_{2222} + C_{13} \overline{G}_{2332} + e_{31} \overline{G}_{2432} } \right\} $$

$$ S_{2222} = \frac{1}{4\pi }\left\{ {C_{12} \overline{G}_{2112} + C_{11} \overline{G}_{2222} + C_{13} \overline{G}_{2332} + e_{31} \overline{G}_{2432} } \right\} $$

$$ S_{2233} = \frac{1}{4\pi }\left\{ {C_{13} \overline{G}_{2112} + C_{13} \overline{G}_{2222} + C_{33} \overline{G}_{2332} + e_{33} \overline{G}_{2432} } \right\} $$

$$ S_{2243} = \frac{1}{4\pi }\left\{ {e_{31} \overline{G}_{2112} + e_{31} \overline{G}_{2222} + e_{33} \overline{G}_{2332} + \kappa_{33} \overline{G}_{2432} } \right\} $$

$$ \begin{aligned} S_{2223} & = S_{2332} = S_{3223} = S_{3232} \\ & = \frac{1}{8\pi }\left\{ {C_{44} \left( {\overline{G}_{2323} + \overline{G}_{3322} } \right) - e_{15} \left( {\overline{G}_{2423} + \overline{G}_{3422} } \right) + C_{44} \left( {\overline{G}_{2233} + \overline{G}_{3232} } \right)} \right\} \\ \end{aligned} $$

$$ \begin{aligned} S_{2342} & = S_{3242} \\ & = \frac{1}{8\pi }\left\{ {e_{15} \left( {\overline{G}_{2323} + \overline{G}_{3322} } \right) - \kappa_{11} \left( {\overline{G}_{2423} + \overline{G}_{3422} } \right) + e_{15} \left( {\overline{G}_{2233} + \overline{G}_{3232} } \right)} \right\} \\ \end{aligned} $$

$$ S_{3311} = \frac{1}{4\pi }\left\{ {C_{11} \overline{G}_{3113} + C_{12} \overline{G}_{3223} + C_{13} \overline{G}_{3333} + e_{31} \overline{G}_{3433} } \right\} $$

$$ S_{3322} = \frac{1}{4\pi }\left\{ {C_{12} \overline{G}_{3113} + C_{11} \overline{G}_{3223} + C_{13} \overline{G}_{3333} + e_{31} \overline{G}_{3433} } \right\} $$

$$ S_{3333} = \frac{1}{4\pi }\left\{ {C_{13} \overline{G}_{3113} + C_{13} \overline{G}_{3223} + C_{33} \overline{G}_{3333} + e_{33} \overline{G}_{3433} } \right\} $$

$$ S_{3343} = \frac{1}{4\pi }\left\{ {e_{31} \overline{G}_{3113} + e_{31} \overline{G}_{3223} + e_{33} \overline{G}_{3333} + \kappa_{33} \overline{G}_{3433} } \right\} $$

$$ S_{4113} = S_{4131} = \frac{1}{4\pi }\left\{ {C_{44} \overline{G}_{4311} + e_{15} \overline{G}_{4411} + C_{44} \overline{G}_{4131} } \right\} $$

$$ S_{4141} = \frac{1}{4\pi }\left\{ {e_{15} \overline{G}_{4311} - \kappa_{11} \overline{G}_{4411} + e_{15} \overline{G}_{4131} } \right\} $$

$$ S_{4223} = S_{4232} = \frac{1}{4\pi }\left\{ {C_{44} \overline{G}_{4322} + e_{15} \overline{G}_{4422} + C_{44} \overline{G}_{4232} } \right\} $$

$$ S_{4242} = \frac{1}{4\pi }\left\{ {e_{15} \overline{G}_{4322} - \kappa_{11} \overline{G}_{4422} + e_{15} \overline{G}_{4232} } \right\} $$

$$ S_{4311} = \frac{1}{4\pi }\left\{ {C_{11} \overline{G}_{4113} + C_{12} \overline{G}_{4223} + C_{13} \overline{G}_{4333} + e_{31} \overline{G}_{4433} } \right\} $$

$$ S_{4322} = \frac{1}{4\pi }\left\{ {C_{12} \overline{G}_{4113} + C_{11} \overline{G}_{4223} + C_{13} \overline{G}_{4333} + e_{31} \overline{G}_{4433} } \right\} $$

$$ S_{4343} = \frac{1}{4\pi }\left\{ {e_{13} \overline{G}_{4113} + e_{31} \overline{G}_{4223} + e_{13} \overline{G}_{4333} + \kappa_{33} \overline{G}_{4433} } \right\} $$

Appendix B

$$ N_{x} = \mathop \int \nolimits_{{ - \frac{h}{2}}}^{\frac{h}{2}} \sigma_{x} dz = A_{11} \frac{\partial u}{{\partial x}} + A_{11} \frac{1}{2}\left( {\frac{\partial w}{{\partial x}}} \right)^{2} + B_{11} \frac{{\partial \varphi_{x} }}{\partial x} + A_{12} \frac{1}{r\left( x \right)}\frac{\partial v}{{\partial \theta }} + A_{12} \frac{sin\alpha }{{r\left( x \right)}}u + A_{12} \frac{cos\alpha }{{r\left( x \right)}}w + A_{12} \frac{1}{{2r\left( x \right)^{2} }}\left( {\frac{\partial w}{{\partial \theta }}} \right)^{2} + B_{12} \frac{1}{r\left( x \right)}\frac{{\partial \varphi_{\theta } }}{\partial \theta } + B_{12} \frac{sin\alpha }{{r\left( x \right)}}\varphi_{x} - A_{31}^{e} \phi - A_{31}^{m} \psi $$

(46a)

$$ N_{\theta } = \mathop \int \nolimits_{{ - \frac{h}{2}}}^{\frac{h}{2}} \sigma_{\theta } dz = A_{12} \frac{\partial u}{{\partial x}} + A_{12} \frac{1}{2}\left( {\frac{\partial w}{{\partial x}}} \right)^{2} + B_{12} \frac{{\partial \varphi_{X} }}{\partial x} + A_{22} \frac{1}{r\left( x \right)}\frac{\partial v}{{\partial \theta }} + A_{22} \frac{sin\alpha }{{r\left( x \right)}}u + A_{22} \frac{cos\alpha }{{r\left( x \right)}}w + A_{22} \frac{1}{{2r\left( x \right)^{2} }}\left( {\frac{\partial w}{{\partial \theta }}} \right)^{2} + B_{22} \frac{1}{r\left( x \right)}\frac{{\partial \varphi_{\theta } }}{\partial \theta } + B_{22} \frac{sin\alpha }{{r\left( x \right)}}\varphi_{x} - A_{32}^{e} \phi - A_{32}^{m} \psi $$

(46b)

$$ N_{x\theta } = \mathop \int \nolimits_{{ - \frac{h}{2}}}^{\frac{h}{2}} \sigma_{x\theta } dz = A_{44} \frac{1}{r\left( x \right)}\frac{\partial u}{{\partial \theta }} - A_{44} \frac{sin\alpha }{{r\left( x \right)}}v + A_{44} \frac{\partial v}{{\partial x}} + A_{44} \frac{1}{r\left( x \right)}\frac{\partial w}{{\partial x}}\frac{\partial w}{{\partial \theta }} + B_{44} \frac{{\partial \varphi_{\theta } }}{\partial x} + B_{44} \frac{1}{r\left( x \right)}\frac{{\partial \varphi_{x} }}{\partial \theta } - B_{44} \frac{sin\alpha }{{r\left( x \right)}}\varphi_{\theta } - A_{24}^{e} \frac{\partial \phi }{{\partial \theta }} - A_{24}^{m} \frac{\partial \psi }{{\partial \theta }} $$

(46c)

$$ M_{x} = \mathop \int \nolimits_{{ - \frac{h}{2}}}^{\frac{h}{2}} \sigma_{x} zdz = B_{11} \frac{\partial u}{{\partial x}} + B_{11} \frac{1}{2}\left( {\frac{\partial w}{{\partial x}}} \right)^{2} + D_{11} \frac{{\partial \varphi_{x} }}{\partial x} + B_{12} \frac{1}{r\left( x \right)}\frac{\partial v}{{\partial \theta }} + B_{12} \frac{sin\alpha }{{r\left( x \right)}}u + B_{12} \frac{cos\alpha }{{r\left( x \right)}}w + B_{12} \frac{1}{{2r\left( x \right)^{2} }}\left( {\frac{\partial w}{{\partial \theta }}} \right)^{2} + D_{12} \frac{1}{r\left( x \right)}\frac{{\partial \varphi_{\theta } }}{\partial \theta } + D_{12} \frac{sin\alpha }{{r\left( x \right)}}\varphi_{x} - B_{31}^{e} \phi - B_{31}^{m} \psi $$

(46d)

$$ M_{\theta } = \mathop \int \nolimits_{{ - \frac{h}{2}}}^{\frac{h}{2}} \sigma_{\theta } zdz = B_{12} \frac{\partial u}{{\partial x}} + B_{12} \frac{1}{2}\left( {\frac{\partial w}{{\partial x}}} \right)^{2} + D_{12} \frac{{\partial \varphi_{x} }}{\partial x} + B_{22} \frac{1}{r\left( x \right)}\frac{\partial v}{{\partial \theta }} + B_{22} \frac{sin\alpha }{{r\left( x \right)}}u + B_{22} \frac{cos\alpha }{{r\left( x \right)}}w + B_{22} \frac{1}{{2r\left( x \right)^{2} }}\left( {\frac{\partial w}{{\partial \theta }}} \right)^{2} + D_{22} \frac{1}{r\left( x \right)}\frac{{\partial \varphi_{\theta } }}{\partial \theta } + D_{22} \frac{sin\alpha }{{r\left( x \right)}}\varphi_{x} - B_{32}^{e} \phi - B_{32}^{m} \psi $$

(46e)

$$ M_{x\theta } = \mathop \int \nolimits_{{ - \frac{h}{2}}}^{\frac{h}{2}} \sigma_{x\theta } zdz = B_{44} \frac{1}{r\left( x \right)}\frac{\partial u}{{\partial \theta }} - B_{44} \frac{sin\alpha }{{r\left( x \right)}}v + B_{44} \frac{\partial v}{{\partial x}} + B_{44} \frac{1}{r\left( x \right)}\frac{\partial w}{{\partial x}}\frac{\partial w}{{\partial \theta }} + D_{44} \frac{{\partial \varphi_{\theta } }}{\partial x} + D_{44} \frac{1}{r\left( x \right)}\frac{{\partial \varphi_{x} }}{\partial \theta } - D_{44} \frac{sin\alpha }{{r\left( x \right)}}\varphi_{\theta } - B_{24}^{e} \phi - B_{24}^{m} \psi $$

(46f)

$$ Q_{x} = k\mathop \int \nolimits_{{ - \frac{h}{2}}}^{\frac{h}{2}} \sigma_{xz} dz = A_{66} \frac{\partial w}{{\partial x}} + A_{66} \varphi_{x} $$

(46g)

$$ Q_{\theta z} = k\mathop \int \nolimits_{{ - \frac{h}{2}}}^{\frac{h}{2}} \sigma_{\theta z} dz = A_{55} \frac{1}{r\left( x \right)}\frac{\partial w}{{\partial \theta }} + A_{55} \varphi_{\theta } - A_{55} \frac{cos\alpha }{{r\left( x \right)}}v - A_{15}^{e} \frac{\partial \phi }{{\partial x}} - A_{15}^{m} \frac{\partial \psi }{{\partial x}} $$

(46h)

$$ \mathop \int \nolimits_{{ - \frac{h}{2}}}^{\frac{h}{2}} \cos \left( {\xi z} \right)\frac{{\partial D_{x} }}{\partial x}dz = \tilde{\kappa }_{11} \frac{{\partial^{2} \phi }}{{\partial x^{2} }} + \tilde{\lambda }_{11} \frac{{\partial^{2} \psi }}{{\partial x^{2} }} $$

(46i)

$$ \mathop \int \nolimits_{{ - \frac{h}{2}}}^{\frac{h}{2}} \frac{1}{R\left( x \right)}\cos \left( {\xi z} \right)\frac{{\partial D_{\theta } }}{\partial \theta }dz = \tilde{\kappa }_{22} \frac{{\partial^{2} \phi }}{{\partial \theta^{2} }} + \tilde{\lambda }_{22} \frac{{\partial^{2} \psi }}{{\partial \theta^{2} }} $$

(46j)

$$ \mathop \int \nolimits_{{ - \frac{h}{2}}}^{\frac{h}{2}} \xi {\text{sin}}\left( {\xi z} \right)D_{z} dz = - A_{31}^{e} \left( {\frac{\partial u}{{\partial x}} + \frac{1}{2}\frac{\partial w}{{\partial x}}\frac{\partial w}{{\partial x}}} \right) - B_{31}^{e} \frac{{\partial \varphi_{x} }}{\partial x} - A_{32}^{e} \left( {\frac{1}{r\left( x \right)}\frac{\partial v}{{\partial \theta }} + \frac{sin\alpha }{{r\left( x \right)}}u + \frac{\cos \alpha }{{r\left( x \right)}}w + \frac{1}{{2r^{2} \left( x \right)}}\left( {\frac{\partial w}{{\partial \theta }}} \right)^{2} { }} \right) - B_{32}^{e} \left( {\frac{1}{r\left( x \right)}\frac{{\partial \varphi_{\theta } }}{\partial \theta } + \frac{sin\alpha }{{r\left( x \right)}}\varphi_{x} } \right) - \tilde{\kappa }_{33} \phi - \tilde{\lambda }_{33} \psi $$

(46k)

$$ \mathop \int \nolimits_{{ - \frac{h}{2}}}^{\frac{h}{2}} \cos \left( {\xi z} \right)\frac{{\partial B_{x} }}{\partial x}dz = \tilde{\lambda }_{11} \frac{{\partial^{2} \phi }}{{\partial x^{2} }} + \tilde{\mu }_{11} \frac{{\partial^{2} \psi }}{{\partial x^{2} }} $$

(46l)

$$ \mathop \int \nolimits_{{ - \frac{h}{2}}}^{\frac{h}{2}} \frac{1}{R\left( x \right)}\cos \left( {\xi z} \right)\frac{{\partial B_{\theta } }}{\partial \theta }dz = \tilde{\lambda }_{22} \frac{{\partial^{2} \phi }}{{\partial \theta^{2} }} + \tilde{\mu }_{22} \frac{{\partial^{2} \psi }}{{\partial \theta^{2} }} $$

(46m)

$$ \mathop \int \nolimits_{{ - \frac{h}{2}}}^{\frac{h}{2}} \xi {\text{sin}}\left( {\xi z} \right)B_{z} dz = - A_{31}^{m} \left( {\frac{\partial u}{{\partial x}} + \frac{1}{2}\frac{\partial w}{{\partial x}}\frac{\partial w}{{\partial x}}} \right) - B_{31}^{m} \frac{{\partial \varphi_{x} }}{\partial x} - A_{32}^{m} \left( {\frac{1}{r\left( x \right)}\frac{\partial v}{{\partial \theta }} + \frac{sin\alpha }{{r\left( x \right)}}u + \frac{\cos \alpha }{{r\left( x \right)}}w + \frac{1}{{2r^{2} \left( x \right)}}\left( {\frac{\partial w}{{\partial \theta }}} \right)^{2} { }} \right) - B_{32}^{m} \left( {\frac{1}{r\left( x \right)}\frac{{\partial \varphi_{\theta } }}{\partial \theta } + \frac{sin\alpha }{{r\left( x \right)}}\varphi_{x} } \right) - \tilde{\lambda }_{33} \phi - \tilde{\mu }_{33} \psi $$

(46n)

The coefficients $A_{ij}$, $B_{ij}$, and $D_{ij}$ are stretching, bending-stretching (coupling), and bending stiffness, respectively. Moreover, it can be expressed from the following relationships:

$$ \left( {A_{ij} ,B_{ij} ,D_{ij} } \right) = \mathop \int \nolimits_{{ - \frac{h}{2}}}^{\frac{h}{2}} \left( {c_{ij} ,zc_{ij} ,z^{2} c_{ij} } \right)dz i,j = 1,2,4 $$

(47a)

$$ A_{ij} = k\mathop \int \nolimits_{{ - \frac{h}{2}}}^{\frac{h}{2}} c_{ij} dz i,j = 5,6 $$

(47b)

Also, the coefficients used in Eq. (46a–n) can be expressed as follows:

$$ \left( {A_{31}^{e} ,B_{31}^{e} } \right) = \mathop \int \nolimits_{{ - \frac{h}{2}}}^{\frac{h}{2}} e_{31} \xi {\text{sin}}\left( {\xi z} \right)\left( {1,z} \right)dz $$

(48a)

$$ \left( {A_{32}^{e} ,B_{32}^{e} } \right) = \mathop \int \nolimits_{{ - \frac{h}{2}}}^{\frac{h}{2}} e_{32} \xi {\text{sin}}\left( {\xi z} \right)\left( {1,z} \right)dz $$

(48b)

$$ \left( {A_{31}^{m} ,B_{31}^{m} } \right) = \mathop \int \nolimits_{{ - \frac{h}{2}}}^{\frac{h}{2}} q_{31} \xi {\text{sin}}\left( {\xi z} \right)\left( {1,z} \right)dz $$

(48c)

$$ \left( {A_{32}^{m} ,B_{32}^{m} } \right) = \mathop \int \nolimits_{{ - \frac{h}{2}}}^{\frac{h}{2}} q_{32} \xi {\text{sin}}\left( {\xi z} \right)\left( {1,z} \right)dz $$

(48d)

$$ \left( {\tilde{\kappa }_{11} ,\tilde{\lambda }_{11} ,\tilde{\mu }_{11} } \right) = \mathop \int \nolimits_{{ - \frac{h}{2}}}^{\frac{h}{2}} \left( {\kappa_{11} ,\lambda_{11} ,\mu_{11} } \right)cos^{2} \left( {\xi z} \right)dz $$

(48e)

$$ \left( {\tilde{\kappa }_{22} ,\tilde{\lambda }_{22} ,\tilde{\mu }_{22} } \right) = \mathop \int \nolimits_{{ - \frac{h}{2}}}^{\frac{h}{2}} \left( {\kappa_{22} ,\lambda_{22} ,\mu_{22} } \right)\left( {\frac{1}{R\left( x \right)}} \right)^{2} cos^{2} \left( {\xi z} \right)dz $$

(48f)

$$ \left( {\tilde{\kappa }_{33} ,\tilde{\lambda }_{33} ,\tilde{\mu }_{33} } \right) = \mathop \int \nolimits_{{ - \frac{h}{2}}}^{\frac{h}{2}} \left( {\kappa_{33} ,\lambda_{33} ,\mu_{33} } \right)\xi^{2} {\text{sin}}^{2} \left( {\xi z} \right)dz $$

(48g)

Appendix C

$${A}_{11}\frac{{\partial }^{2}u}{{\partial x}^{2}}+\frac{{A}_{11}sin\alpha }{r(x)}\frac{\partial u}{\partial x}-\frac{{A}_{22}{sin}^{2}\alpha }{{r\left(x\right)}^{2}}u+\frac{{A}_{44}}{r{\left(x\right)}^{2}}\frac{{\partial }^{2}u}{{\partial \theta }^{2}}-\frac{\left({A}_{44}+{A}_{22}\right)sin\alpha }{{r\left(x\right)}^{2}}\frac{\partial v}{\partial \theta }+\frac{\left({A}_{12}+{A}_{44}\right)}{r\left(x\right)}\frac{{\partial }^{2}v}{\partial x\partial \theta }+\frac{{A}_{12}cos\alpha }{r\left(x\right)}\frac{\partial w}{\partial x}-\frac{{A}_{12}sin\alpha cos\alpha }{{r\left(x\right)}^{2}}w+{B}_{11}\frac{{\partial }^{2}{\varphi }_{x}}{{\partial x}^{2}}+\frac{{B}_{11}sin\alpha }{r\left(x\right)}\frac{\partial {\varphi }_{x}}{\partial x}+\frac{{B}_{44}}{r{\left(x\right)}^{2}}\frac{{\partial }^{2}{\varphi }_{x}}{{\partial \theta }^{2}}-\frac{{{B}_{22}sin}^{2}\alpha }{{r\left(x\right)}^{2}}{\varphi }_{x}-\frac{\left({B}_{44}+{B}_{22}\right)sin\alpha }{{r\left(x\right)}^{2}}\frac{\partial {\varphi }_{\theta }}{\partial \theta }+\frac{\left({B}_{44}+{B}_{12}\right)}{r\left(x\right)}\frac{{\partial }^{2}{\varphi }_{\theta }}{\partial x\partial \theta }+{A}_{11}\frac{{\partial }^{2}w}{{\partial x}^{2}}\frac{\partial w}{\partial x}+\frac{\left({A}_{11}-{A}_{12}\right)sin\alpha }{2r\left(x\right)}\frac{\partial w}{\partial x}\frac{\partial w}{\partial x}+\frac{{A}_{44}}{r{\left(x\right)}^{2}}\frac{{\partial }^{2}w}{{\partial \theta }^{2}}\frac{\partial w}{\partial x}-\frac{{A}_{12}sin\alpha }{r{\left(x\right)}^{3}}\frac{\partial w}{\partial \theta }\frac{\partial w}{\partial \theta }-\frac{\left({A}_{12}-{A}_{22}\right)sin\alpha }{2r{\left(x\right)}^{3}}\frac{\partial w}{\partial \theta }\frac{\partial w}{\partial \theta }+\frac{\left({A}_{12}+{A}_{44}\right)}{r{\left(x\right)}^{2}}\frac{{\partial }^{2}w}{\partial x\partial \theta }\frac{\partial w}{\partial \theta }-{A}_{31}^{e}\frac{\partial \phi }{\partial x}-\frac{{A}_{24}^{e}}{r\left(x\right)}\frac{{\partial }^{2}\phi }{{\partial \theta }^{2}}+\frac{\left(-{A}_{31}^{e}+{A}_{32}^{e}\right)sin\alpha }{r\left(x\right)}\phi -{A}_{31}^{m}\frac{\partial \psi }{\partial x}-\frac{{A}_{24}^{m}}{r\left(x\right)}\frac{{\partial }^{2}\psi }{{\partial \theta }^{2}}+\frac{\left(-{A}_{31}^{m}+{A}_{32}^{m}\right)sin\alpha }{r\left(x\right)}\psi ={I}_{0}\frac{{\partial }^{2}u}{{\partial t}^{2}}+{I}_{1}\frac{{\partial }^{2}{\varphi }_{x}}{{\partial t}^{2}}$$

(49a)

$$\frac{\left({A}_{44}+{A}_{22}\right)sin\alpha }{{r\left(x\right)}^{2}}\frac{\partial u}{\partial \theta }+\frac{\left({A}_{44}+{A}_{12}\right)}{r\left(x\right)}\frac{{\partial }^{2}u}{\partial x\partial \theta }+{A}_{44}\frac{{\partial }^{2}v}{{\partial x}^{2}}+\frac{{A}_{22}}{{r\left(x\right)}^{2}}\frac{{\partial }^{2}v}{{\partial \theta }^{2}}+\frac{{A}_{44}sin\alpha }{r\left(x\right)}\frac{\partial v}{\partial x}-\frac{{A}_{44}{sin}^{2}\alpha }{{r\left(x\right)}^{2}}v-\frac{{A}_{55}{cos}^{2}\alpha }{{r\left(x\right)}^{2}}v+\frac{\left({A}_{22}+{A}_{55}\right)cos\alpha }{{r\left(x\right)}^{2}}\frac{\partial w}{\partial \theta }-\frac{\left({B}_{44}+{B}_{22}\right)sin\alpha }{{r\left(x\right)}^{2}}\frac{\partial {\varphi }_{x}}{\partial \theta }+\frac{\left({B}_{44}+{B}_{12}\right)}{r\left(x\right)}\frac{{\partial }^{2}{\varphi }_{x}}{\partial x\partial \theta }+{B}_{44}\frac{{\partial }^{2}{\varphi }_{\theta }}{{\partial x}^{2}}+\frac{{B}_{22}}{{r\left(x\right)}^{2}}\frac{{\partial }^{2}{\varphi }_{\theta }}{{\partial \theta }^{2}}+\frac{{B}_{44}sin\alpha }{r\left(x\right)}\frac{\partial {\varphi }_{\theta }}{\partial x}+{A}_{55}\frac{cos\alpha }{r\left(x\right)} {\varphi }_{\theta }- \frac{{B}_{44}{sin}^{2}\alpha }{{r\left(x\right)}^{2}}{\varphi }_{\theta }+\frac{{A}_{44}}{r\left(x\right)}\frac{{\partial }^{2}w}{{\partial x}^{2}}\frac{\partial w}{\partial \theta }+ \frac{{A}_{44}sin\alpha }{{r\left(x\right)}^{2}}\frac{\partial w}{\partial x}\frac{\partial w}{\partial \theta }+\frac{{A}_{22}}{{r\left(x\right)}^{3}}\frac{{\partial }^{2}w}{{\partial \theta }^{2}}\frac{\partial w}{\partial \theta }+\frac{\left({A}_{44}+{A}_{12}\right)}{r\left(x\right)}\frac{{\partial }^{2}w}{\partial x\partial \theta }\frac{\partial w}{\partial x}-\frac{{A}_{32}^{e}}{r\left(x\right)}\frac{\partial \phi }{\partial \theta }- {A}_{24}^{e}\frac{{\partial }^{2}\phi }{\partial x\partial \theta }-\frac{2{A}_{24}^{e}sin\alpha }{r\left(x\right)}\frac{\partial \phi }{\partial \theta }-{A}_{15}^{e}\frac{cos\alpha }{r(x)}\frac{\partial \phi }{\partial x}-\frac{{A}_{32}^{m}}{r\left(x\right)}\frac{\partial \psi }{\partial \theta }- {A}_{24}^{m}\frac{{\partial }^{2}\psi }{\partial x\partial \theta }-\frac{2{A}_{24}^{m}sin\alpha }{r\left(x\right)}\frac{\partial \psi }{\partial \theta }-{A}_{15}^{m}\frac{cos\alpha }{r(x)}\frac{\partial \psi }{\partial x}={I}_{0}\frac{{\partial }^{2}v}{{\partial t}^{2}}+{I}_{1}\frac{{\partial }^{2}{\varphi }_{\theta }}{{\partial t}^{2}}$$

(49b)

$$-{A}_{12}\frac{cos\alpha }{r\left(x\right)}\frac{\partial u}{\partial x}- \frac{{A}_{22}sin\alpha cos\alpha }{{r\left(x\right)}^{2}}u-\frac{{A}_{22}cos\alpha }{{r\left(x\right)}^{2}} \frac{\partial v}{\partial \theta }-\frac{{A}_{55}cos\alpha }{{r\left(x\right)}^{2}}\frac{\partial v}{\partial \theta }+{A}_{66}\frac{{\partial }^{2}w}{{\partial x}^{2}}-{A}_{66}\frac{sin\alpha }{r(x)}\frac{\partial w}{\partial x}+\frac{{A}_{55}}{{r(x)}^{2}}\frac{{\partial }^{2}w}{{\partial \theta }^{2}}-\frac{{A}_{22}{cos}^{2}\alpha }{{r(x)}^{2}} w+{A}_{66}\frac{\partial {\varphi }_{x}}{\partial x}-{B}_{12}\frac{cos\alpha }{r(x)} \frac{\partial {\varphi }_{x}}{\partial x}-{A}_{66}\frac{sin\alpha }{r(x)}{\varphi }_{x}-\frac{{B}_{22}sin\alpha cos\alpha }{{r(x)}^{2}} {\varphi }_{x}+\frac{{A}_{55}}{r(x)}\frac{\partial {\varphi }_{\theta }}{\partial \theta }-{B}_{22}\frac{cos\alpha }{{r(x)}^{2}} \frac{\partial {\varphi }_{\theta }}{\partial \theta }-\frac{{A}_{12}cos\alpha }{r(x)} \frac{\partial w}{\partial x}\frac{\partial w}{\partial x}-\frac{{A}_{22}cos\alpha }{2{r(x)}^{3}} \frac{\partial w}{\partial \theta }\frac{\partial w}{\partial \theta }-\frac{{A}_{15}^{e}}{r(x)}\frac{{\partial }^{2}\phi }{\partial x\partial \theta }-\frac{{A}_{32}^{e}cos\alpha }{r(x)}\phi -\frac{{A}_{15}^{m}}{r(x)}\frac{{\partial }^{2}\psi }{\partial x\partial \theta }-\frac{{A}_{32}^{m}cos\alpha }{r(x)}\psi ={I}_{0}\frac{{\partial }^{2}w}{{\partial t}^{2}}$$

(49c)

$${B}_{11}\frac{{\partial }^{2}u}{{\partial x}^{2}}+\frac{{B}_{44}}{{r(x)}^{2}}\frac{{\partial }^{2}u}{{\partial \theta }^{2}}+\frac{{B}_{11}sin\alpha }{r(x)}\frac{\partial u}{\partial x}-{B}_{22}\frac{{sin}^{2}\alpha }{{r\left(x\right)}^{2}}u-\frac{\left({B}_{22}+{B}_{44}\right)sin\alpha }{{r\left(x\right)}^{2}}\frac{\partial v}{\partial \theta }+\frac{\left({B}_{12}+{B}_{44}\right)}{r\left(x\right)}\frac{{\partial }^{2}v}{\partial x\partial \theta }+{B}_{12}\frac{cos\alpha }{r\left(x\right)}\frac{\partial w}{\partial x}-{A}_{66}\frac{\partial w}{\partial x}-\frac{{B}_{22}\mathrm{sin}\alpha \mathrm{cos}\alpha }{{r\left(x\right)}^{2}}w+{D}_{11}\frac{{\partial }^{2}{\varphi }_{x}}{{\partial x}^{2}}+\frac{{D}_{44}}{{r\left(x\right)}^{2}}\frac{{\partial }^{2}{\varphi }_{x}}{{\partial \theta }^{2}}+\frac{{D}_{11}\mathrm{sin}\alpha }{r\left(x\right)}\frac{\partial {\varphi }_{x}}{\partial x}-\frac{{D}_{22}{sin}^{2}\alpha }{{r\left(x\right)}^{2}}{\varphi }_{x}-{A}_{66}{\varphi }_{x}-\frac{\left({D}_{44}+{D}_{22}\right)sin\alpha }{{r\left(x\right)}^{2}}\frac{\partial {\varphi }_{\theta }}{\partial \theta }+\frac{\left({D}_{12}+{D}_{44}\right)}{r\left(x\right)}\frac{{\partial }^{2}{\varphi }_{\theta }}{\partial x\partial \theta }+{B}_{11}\frac{{\partial }^{2}w}{{\partial x}^{2}}\frac{\partial w}{\partial x}-\frac{{B}_{22}sin\alpha }{{2r\left(x\right)}^{3}}\frac{\partial w}{\partial \theta }\frac{\partial w}{\partial \theta }+\frac{\left({B}_{11}-{B}_{12}\right)\mathrm{sin}\alpha }{2r\left(x\right)}\frac{\partial w}{\partial x}\frac{\partial w}{\partial x}+\frac{\left({B}_{12}+{B}_{44}\right)}{{r\left(x\right)}^{2}}\frac{{\partial }^{2}w}{\partial x\partial \theta }\frac{\partial w}{\partial \theta }+\frac{{B}_{44}}{{r\left(x\right)}^{2}}\frac{{\partial }^{2}w}{{\partial \theta }^{2}}\frac{\partial w}{\partial \theta }-{B}_{31}^{e}\frac{\partial \phi }{\partial x}-\frac{{B}_{24}^{e}}{r\left(x\right)}\frac{\partial \phi }{\partial \theta }-{B}_{31}^{e}\frac{sin\alpha }{r\left(x\right)}\phi +{B}_{32}^{e}\frac{sin\alpha }{r\left(x\right)}\phi -{B}_{31}^{m}\frac{\partial \psi }{\partial x}-\frac{{B}_{24}^{m}}{r\left(x\right)}\frac{\partial \psi }{\partial \theta }-{B}_{31}^{m}\frac{sin\alpha }{r\left(x\right)}\psi +{B}_{32}^{m}\frac{sin\alpha }{r\left(x\right)}\psi ={I}_{1}\frac{{\partial }^{2}u}{{\partial t}^{2}}+{I}_{2}\frac{{\partial }^{2}{\varphi }_{x}}{{\partial t}^{2}}$$

(49d)

$$\frac{\left({B}_{44}+{B}_{12}\right)}{r(x)}\frac{{\partial }^{2}u}{\partial x\partial \theta }+\frac{\left({B}_{44}+{B}_{22}\right)sin\alpha }{{r(x)}^{2}}\frac{\partial u}{\partial \theta }+{B}_{44}\frac{{\partial }^{2}v}{{\partial x}^{2}}+\frac{{B}_{22}}{{r(x)}^{2}}\frac{{\partial }^{2}v}{{\partial \theta }^{2}}+\frac{{B}_{44}\mathrm{sin}\alpha }{r(x)}\frac{\partial v}{\partial x}+\frac{{A}_{55}\mathrm{cos}\alpha }{r(x)}v+\frac{{B}_{22}\mathrm{cos}\alpha }{{r(x)}^{2}}\frac{\partial w}{\partial \theta }-\frac{{A}_{55}}{r\left(x\right)}\frac{\partial w}{\partial \theta }+\frac{\left({D}_{44}+{D}_{12}\right)}{r\left(x\right)}\frac{{\partial }^{2}{\varphi }_{x}}{\partial x\partial \theta }+\frac{\left({D}_{22}+{D}_{44}\right)\mathrm{sin}\alpha }{{r\left(x\right)}^{2}}\frac{\partial {\varphi }_{x}}{\partial \theta }+{D}_{44}\frac{{\partial }^{2}{\varphi }_{\theta }}{{\partial x}^{2}}+\frac{{D}_{22}}{{r\left(x\right)}^{2}}\frac{{\partial }^{2}{\varphi }_{\theta }}{{\partial \theta }^{2}}+\frac{{D}_{44}sin\alpha }{r\left(x\right)}\frac{\partial {\varphi }_{\theta }}{\partial x}-\frac{{D}_{44}{sin}^{2}\alpha }{{r\left(x\right)}^{2}}{\varphi }_{\theta }-{A}_{55}{\varphi }_{\theta }+\frac{{B}_{44}}{r\left(x\right)}\frac{{\partial }^{2}w}{{\partial x}^{2}}\frac{\partial w}{\partial \theta }+\frac{{B}_{22}}{{r\left(x\right)}^{3}}\frac{{\partial }^{2}w}{{\partial \theta }^{2}}\frac{\partial w}{\partial \theta }+\frac{\left({B}_{44}+{B}_{12}\right)}{r\left(x\right)}\frac{{\partial }^{2}w}{\partial x\partial \theta }\frac{\partial w}{\partial x}+\frac{{B}_{44}sin\alpha }{{r\left(x\right)}^{2}}\frac{\partial w}{\partial x}\frac{\partial w}{\partial \theta }-{B}_{24}^{e}\frac{\partial \phi }{\partial x}-\frac{{B}_{32}^{e}}{r\left(x\right)}\phi -\frac{2{B}_{24}^{e}sin\alpha }{r\left(x\right)}\phi +{A}_{15}^{e}\frac{\partial \phi }{\partial x}-{B}_{24}^{m}\frac{\partial \psi }{\partial x}-\frac{{B}_{32}^{m}}{r\left(x\right)}\psi -\frac{2{B}_{24}^{m}sin\alpha }{r\left(x\right)}\psi +{A}_{15}^{e}\frac{\partial \psi }{\partial x}={I}_{1}\frac{{\partial }^{2}v}{{\partial t}^{2}}+{I}_{2}\frac{{\partial }^{2}{\varphi }_{\theta }}{{\partial t}^{2}}$$

(49e)

$${-A}_{31}^{e}\frac{\partial u}{\partial x}-\frac{{A}_{32}^{e}sin\alpha }{r\left(x\right)}u-\frac{{A}_{32}^{e}}{r\left(x\right)}\frac{\partial v}{\partial \theta }-\frac{{A}_{32}^{e}cos\alpha }{r\left(x\right)}w-{B}_{31}^{e}\frac{\partial {\varphi }_{x}}{\partial x}-\frac{{B}_{32}^{e}sin\alpha }{r\left(x\right)}{\varphi }_{x}-\frac{{B}_{32}^{e}}{r\left(x\right)}\frac{\partial {\varphi }_{\theta }}{\partial \theta }-{A}_{31}^{e}\frac{1}{2}\frac{\partial w}{\partial x}\frac{\partial w}{\partial x}-\frac{{A}_{32}^{e}}{2{r\left(x\right)}^{2}}\frac{\partial w}{\partial \theta }\frac{\partial w}{\partial \theta }+{\widetilde{\kappa }}_{11}\frac{{\partial }^{2}\phi }{{\partial x}^{2}}+{\widetilde{\kappa }}_{22}\frac{{\partial }^{2}\phi }{{\partial \theta }^{2}}-{\widetilde{\kappa }}_{33}\phi +{\widetilde{\lambda }}_{11}\frac{{\partial }^{2}\psi }{{\partial x}^{2}}+{\widetilde{\lambda }}_{22}\frac{{\partial }^{2}\psi }{{\partial \theta }^{2}}-{\widetilde{\lambda }}_{33}\psi =0$$

(49f)

$${-A}_{31}^{m}\frac{\partial u}{\partial x}-\frac{{A}_{32}^{m}sin\alpha }{r\left(x\right)}u-\frac{{A}_{32}^{m}}{r\left(x\right)}\frac{\partial v}{\partial \theta }-\frac{{A}_{32}^{m}cos\alpha }{r\left(x\right)}w-{B}_{31}^{m}\frac{\partial {\varphi }_{x}}{\partial x}-\frac{{B}_{32}^{m}sin\alpha }{r\left(x\right)}{\varphi }_{x}-\frac{{B}_{32}^{m}}{r\left(x\right)}\frac{\partial {\varphi }_{\theta }}{\partial \theta }-{A}_{31}^{m}\frac{1}{2}\frac{\partial w}{\partial x}\frac{\partial w}{\partial x}-\frac{{A}_{32}^{m}}{2{r\left(x\right)}^{2}}\frac{\partial w}{\partial \theta }\frac{\partial w}{\partial \theta }+{\widetilde{\lambda }}_{11}\frac{{\partial }^{2}\phi }{{\partial x}^{2}}+{\widetilde{\lambda }}_{22}\frac{{\partial }^{2}\phi }{{\partial \theta }^{2}}-{\widetilde{\lambda }}_{33}\phi +{\widetilde{\mu }}_{11}\frac{{\partial }^{2}\psi }{{\partial x}^{2}}+{\widetilde{\mu }}_{22}\frac{{\partial }^{2}\psi }{{\partial \theta }^{2}}-{\widetilde{\mu }}_{33}\psi =0$$

(49g)

The following boundary conditions are also obtained:

• Clamped boundary conditions:

$$ u = v = w = \varphi_{x} = \varphi_{\theta } = 0{ }\quad x = 0,x = L $$

(50a)

$$ u = v = w = \varphi_{x} = \varphi_{\theta } = 0{ }\quad {\uptheta } = 0,\theta = \theta_{0} $$

(50b)

• Simply supported boundary condition:

  $$ A_{11} \frac{\partial u}{{\partial x}} + B_{11} \frac{{\partial \varphi_{x} }}{\partial x} + A_{12} \frac{sin\alpha }{{a_{0} }}u + B_{12} \frac{sin\alpha }{{a_{0} }}\varphi_{x} = 0{ }\quad x = 0,\;x = L $$
  $$ B_{11} \frac{\partial u}{{\partial x}} + D_{11} \frac{{\partial \varphi_{x} }}{\partial x} + B_{12} \frac{sin\alpha }{{a_{0} }}u + D_{12} \frac{sin\alpha }{{a_{0} }}\varphi_{x} = 0 $$

  (50a)
  $$ A_{22} \frac{1}{r\left( x \right)}\frac{\partial v}{{\partial \theta }} + B_{22} \frac{1}{r\left( x \right)}\frac{{\partial \varphi_{\theta } }}{\partial \theta } = 0\quad {\uptheta } = 0,\theta = \theta_{0} $$
  $$ B_{22} \frac{1}{r\left( x \right)}\frac{\partial v}{{\partial \theta }} + D_{22} \frac{1}{r\left( x \right)}\frac{{\partial \varphi_{\theta } }}{\partial \theta } = 0 $$

  (51b)

Appendix D

$${A}_{11}\left(\sum_{n=1}^{{N}_{x}}{A}_{in}^{x\left(2\right)} {U}_{nj}\right)+\frac{{A}_{11}sin\alpha }{r(x)}\left(\sum_{n=1}^{{N}_{x}}{A}_{in}^{x(1)} {U}_{nj}\right)-\frac{{A}_{22}{sin}^{2}\alpha }{{r\left(x\right)}^{2}}\left({U}_{ij}\right)+\frac{{A}_{44}}{r{\left(x\right)}^{2}}\left(\sum_{m=1}^{{N}_{\theta }}{A}_{jm}^{\theta \left(2\right)} {U}_{im}\right)-\frac{\left({A}_{44}+{A}_{22}\right)sin\alpha }{{r\left(x\right)}^{2}}\left(\sum_{m=1}^{{N}_{\theta }}{A}_{jm}^{\theta \left(1\right)} {V}_{im}\right)+\frac{\left({A}_{12}+{A}_{44}\right)}{r\left(x\right)}\left(\sum_{n=1}^{{N}_{x}}\sum_{m=1}^{{N}_{\theta }}{A}_{in}^{x\left(1\right)}{A}_{jm}^{\theta \left(1\right)} {V}_{nm}\right)+\frac{{A}_{12}cos\alpha }{r\left(x\right)}\left(\sum_{n=1}^{{N}_{x}}{A}_{in}^{x\left(1\right)} {W}_{nj}\right)-\frac{{A}_{12}sin\alpha cos\alpha }{{r\left(x\right)}^{2}}\left({U}_{ij}\right)+{B}_{11}\left(\sum_{n=1}^{{N}_{x}}{A}_{in}^{x\left(2\right)} {{\phi }_{x}}_{nj}\right)+\frac{{B}_{11}sin\alpha }{r\left(x\right)}\left(\sum_{n=1}^{{N}_{x}}{A}_{in}^{x\left(1\right)} {{\phi }_{x}}_{nj}\right)+\frac{{B}_{44}}{r{\left(x\right)}^{2}}\left(\sum_{m=1}^{{N}_{\theta }}{A}_{jm}^{\theta \left(2\right)} {{\phi }_{x}}_{im}\right)-\frac{{{B}_{22}sin}^{2}\alpha }{{r\left(x\right)}^{2}}\left({{\phi }_{x}}_{ij}\right)-\frac{\left({B}_{44}+{B}_{22}\right)sin\alpha }{{r\left(x\right)}^{2}}\left(\sum_{m=1}^{{N}_{\theta }}{A}_{jm}^{\theta \left(1\right)} {{\phi }_{\theta }}_{im}\right)+\frac{\left({B}_{44}+{B}_{12}\right)}{r\left(x\right)}\left(\sum_{n=1}^{{N}_{x}}\sum_{m=1}^{{N}_{\theta }}{A}_{in}^{x\left(1\right)}{A}_{jm}^{\theta \left(1\right)} {{\phi }_{\theta }}_{nm}\right)+{A}_{11}\left(\sum_{n=1}^{{N}_{x}}{A}_{in}^{x\left(2\right)} {W}_{nj}\right)\left(\sum_{n=1}^{{N}_{x}}{A}_{in}^{x\left(1\right)} {W}_{nj}\right)+\frac{\left({A}_{11}-{A}_{12}\right)sin\alpha }{2r\left(x\right)}\left(\sum_{n=1}^{{N}_{x}}{A}_{in}^{x\left(1\right)} {W}_{nj}\right)\left(\sum_{n=1}^{{N}_{x}}{A}_{in}^{x\left(1\right)} {W}_{nj}\right)+\frac{{A}_{44}}{r{\left(x\right)}^{2}}\left(\sum_{m=1}^{{N}_{\theta }}{A}_{im}^{\theta \left(2\right)} {W}_{mj}\right)\left(\sum_{n=1}^{{N}_{x}}{A}_{in}^{x\left(1\right)} {W}_{nj}\right)-\frac{{A}_{12}sin\alpha }{r{\left(x\right)}^{3}}\left(\sum_{m=1}^{{N}_{\theta }}{A}_{im}^{\theta \left(1\right)} {W}_{mj}\right)\left(\sum_{m=1}^{{N}_{\theta }}{A}_{im}^{\theta \left(1\right)} {W}_{mj}\right)-\frac{\left({A}_{12}-{A}_{22}\right)sin\alpha }{2r{\left(x\right)}^{3}}\left(\sum_{m=1}^{{N}_{\theta }}{A}_{im}^{\theta \left(1\right)} {W}_{mj}\right)\left(\sum_{m=1}^{{N}_{\theta }}{A}_{im}^{\theta \left(1\right)} {W}_{mj}\right)+\frac{\left({A}_{12}+{A}_{44}\right)}{r{\left(x\right)}^{2}}\left(\sum_{n=1}^{{N}_{x}}\sum_{m=1}^{{N}_{\theta }}{A}_{in}^{x\left(1\right)}{A}_{jm}^{\theta \left(1\right)} {W}_{nm}\right)\left(\sum_{m=1}^{{N}_{\theta }}{A}_{im}^{\theta \left(1\right)} {W}_{mj}\right)-{A}_{31}^{e}\left(\sum_{n=1}^{{N}_{x}}{A}_{in}^{x\left(1\right)} {\Phi }_{nj}\right)-\frac{{A}_{24}^{e}}{r\left(x\right)}\left(\sum_{m=1}^{{N}_{\theta }}{A}_{im}^{\theta \left(1\right)} {\Phi }_{mj}\right)+\frac{\left(-{A}_{31}^{e}+{A}_{32}^{e}\right)sin\alpha }{r\left(x\right)}\left({\Phi }_{ij}\right)-{A}_{31}^{m}\left(\sum_{n=1}^{{N}_{x}}{A}_{in}^{x\left(1\right)} {\Psi }_{nj}\right)-\frac{{A}_{24}^{m}}{r\left(x\right)}\left(\sum_{m=1}^{{N}_{\theta }}{A}_{im}^{\theta \left(1\right)} {\Psi }_{mj}\right)+\frac{\left(-{A}_{31}^{m}+{A}_{32}^{m}\right)sin\alpha }{r\left(x\right)}\left({\Psi }_{ij}\right)=-{\omega }^{2}{(I}_{0}{U}_{ij}+{I}_{1}{{\phi }_{x}}_{ij})$$

(52a)

$$\frac{\left({A}_{44}+{A}_{22}\right)sin\alpha }{{r\left(x\right)}^{2}}\left(\sum_{m=1}^{{N}_{\theta }}{A}_{jm}^{\theta \left(1\right)} {U}_{im}\right)+\frac{\left({A}_{44}+{A}_{12}\right)}{r\left(x\right)}\left(\sum_{n=1}^{{N}_{x}}\sum_{m=1}^{{N}_{y}}{A}_{in}^{x(1)}{A}_{jm}^{\theta (1)} {U}_{nm}\right)+{A}_{44}\left(\sum_{n=1}^{{N}_{x}}{A}_{in}^{x(2)} {V}_{nj}\right)+\frac{{A}_{22}}{{r\left(x\right)}^{2}}\left(\sum_{m=1}^{{N}_{\theta }}{A}_{jm}^{\theta \left(2\right)} {V}_{im}\right)+\frac{{A}_{44}sin\alpha }{r\left(x\right)}\left(\sum_{n=1}^{{N}_{x}}{A}_{in}^{x(1)} {V}_{nj}\right)-\frac{{A}_{44}{sin}^{2}\alpha }{{r\left(x\right)}^{2}}\left({V}_{ij}\right)-\frac{{A}_{55}{cos}^{2}\alpha }{{r\left(x\right)}^{2}}\left({V}_{ij}\right)+\frac{\left({A}_{22}+{A}_{55}\right)cos\alpha }{{r\left(x\right)}^{2}}\left(\sum_{m=1}^{{N}_{\theta }}{A}_{jm}^{\theta \left(1\right)} {W}_{im}\right)-\frac{\left({B}_{44}+{B}_{22}\right)sin\alpha }{{r\left(x\right)}^{2}}\left(\sum_{m=1}^{{N}_{\theta }}{A}_{jm}^{\theta \left(1\right)} {{\phi }_{x}}_{im}\right)+\frac{\left({B}_{44}+{B}_{12}\right)}{r\left(x\right)}\left(\sum_{n=1}^{{N}_{x}}\sum_{m=1}^{{N}_{y}}{A}_{in}^{x(1)}{A}_{jm}^{\theta (1)} {{\phi }_{x}}_{nm}\right)+{B}_{44}\left(\sum_{n=1}^{{N}_{x}}{A}_{in}^{x(2)} {{\phi }_{\theta }}_{nj}\right)+\frac{{B}_{22}}{{r\left(x\right)}^{2}}\left(\sum_{m=1}^{{N}_{\theta }}{A}_{jm}^{\theta \left(2\right)} {{\phi }_{\theta }}_{im}\right)+\frac{{B}_{44}sin\alpha }{r\left(x\right)}\left(\sum_{m=1}^{{N}_{\theta }}{A}_{jm}^{\theta \left(1\right)} {{\phi }_{\theta }}_{im}\right)+{A}_{55}\frac{cos\alpha }{r\left(x\right)} \left({{\phi }_{\theta }}_{ij}\right)- \frac{{B}_{44}{sin}^{2}\alpha }{{r\left(x\right)}^{2}}\left({{\phi }_{\theta }}_{ij}\right)+\frac{{A}_{44}}{r\left(x\right)}\left(\sum_{n=1}^{{N}_{x}}{A}_{in}^{x(2)} {W}_{nj}\right)\left(\sum_{m=1}^{{N}_{\theta }}{A}_{jm}^{\theta \left(1\right)} {W}_{im}\right)+ \frac{{A}_{44}sin\alpha }{{r\left(x\right)}^{2}}\left(\sum_{n=1}^{{N}_{x}}{A}_{in}^{x(1)} {W}_{nj}\right)\left(\sum_{n=1}^{{N}_{x}}{A}_{in}^{x(1)} {W}_{nj}\right)+\frac{{A}_{22}}{{r\left(x\right)}^{3}}\left(\sum_{m=1}^{{N}_{\theta }}{A}_{jm}^{\theta \left(2\right)} {W}_{im}\right)\left(\sum_{m=1}^{{N}_{\theta }}{A}_{jm}^{\theta \left(1\right)} {W}_{im}\right)+\frac{\left({A}_{44}+{A}_{12}\right)}{r\left(x\right)}\left(\sum_{n=1}^{{N}_{x}}\sum_{m=1}^{{N}_{y}}{A}_{in}^{x(1)}{A}_{jm}^{\theta (1)} {W}_{nm}\right)\left(\sum_{n=1}^{{N}_{x}}{A}_{in}^{x(1)} {W}_{nj}\right)-\frac{{A}_{32}^{e}}{r\left(x\right)}\left(\sum_{m=1}^{{N}_{\theta }}{A}_{jm}^{\theta \left(1\right)} {\Phi }_{im}\right)- {A}_{24}^{e}\left(\sum_{n=1}^{{N}_{x}}\sum_{m=1}^{{N}_{y}}{A}_{in}^{x(1)}{A}_{jm}^{\theta (1)} {\Phi }_{nm}\right)-\frac{2{A}_{24}^{e}sin\alpha }{r\left(x\right)}\left(\sum_{m=1}^{{N}_{\theta }}{A}_{jm}^{\theta \left(1\right)} {\Phi }_{im}\right)-{A}_{15}^{e}\frac{cos\alpha }{r(x)}\left(\sum_{n=1}^{{N}_{x}}{A}_{in}^{x(1)} {\Phi }_{nj}\right)-\frac{{A}_{32}^{m}}{r\left(x\right)}\left(\sum_{m=1}^{{N}_{\theta }}{A}_{jm}^{\theta \left(1\right)} {\Psi }_{im}\right)- {A}_{24}^{m}\left(\sum_{n=1}^{{N}_{x}}\sum_{m=1}^{{N}_{y}}{A}_{in}^{x(1)}{A}_{jm}^{\theta (1)} {\Psi }_{nm}\right)-\frac{2{A}_{24}^{m}sin\alpha }{r\left(x\right)}\left(\sum_{m=1}^{{N}_{\theta }}{A}_{jm}^{\theta \left(1\right)} {\Psi }_{im}\right)-{A}_{15}^{m}\frac{cos\alpha }{r(x)}\left(\sum_{n=1}^{{N}_{x}}{A}_{in}^{x(1)} {\Psi }_{nj}\right)=-{\omega }^{2}{(I}_{0}{V}_{ij}+{I}_{1}{{\phi }_{\theta }}_{ij})$$

(52b)

$$-{A}_{12}\frac{cos\alpha }{r\left(x\right)}\left(\sum_{n=1}^{{N}_{x}}{A}_{in}^{x\left(1\right)} {U}_{nj}\right)- \frac{{A}_{22}sin\alpha cos\alpha }{{r\left(x\right)}^{2}}\left({U}_{ij}\right)-\frac{{A}_{22}cos\alpha }{{r\left(x\right)}^{2}} \left(\sum_{m=1}^{{N}_{\theta }}{A}_{jm}^{\theta \left(1\right)} {V}_{im}\right)-\frac{{A}_{55}cos\alpha }{{r\left(x\right)}^{2}} \left(\sum_{m=1}^{{N}_{\theta }}{A}_{jm}^{\theta \left(1\right)} {V}_{im}\right)+{A}_{66}\left(\sum_{n=1}^{{N}_{x}}{A}_{in}^{x\left(2\right)} {W}_{nj}\right)+{A}_{66}\frac{sin\alpha }{r\left(x\right)}\left(\sum_{n=1}^{{N}_{x}}{A}_{in}^{x\left(1\right)} {W}_{nj}\right)+\frac{{A}_{55}}{{r\left(x\right)}^{2}}\left(\sum_{m=1}^{{N}_{\theta }}{A}_{jm}^{\theta \left(2\right)} {W}_{im}\right)-\frac{{A}_{22}{cos}^{2}\alpha }{{r\left(x\right)}^{2}} \left({W}_{ij}\right)+{A}_{66}\left(\sum_{n=1}^{{N}_{x}}{A}_{in}^{x\left(1\right)} {{\phi }_{x}}_{nj}\right)-{B}_{12}\frac{cos\alpha }{r\left(x\right)} \left(\sum_{n=1}^{{N}_{x}}{A}_{in}^{x\left(1\right)} {{\phi }_{x}}_{nj}\right)+{A}_{66}\frac{sin\alpha }{r(x)}\left({{\phi }_{x}}_{ij}\right)-\frac{{B}_{22}sin\alpha cos\alpha }{{r(x)}^{2}} \left({{\phi }_{x}}_{ij}\right)+\frac{{A}_{55}}{r(x)}\left(\sum_{m=1}^{{N}_{\theta }}{A}_{jm}^{\theta \left(1\right)} {{\phi }_{\theta }}_{im}\right)-{B}_{22}\frac{cos\alpha }{{r(x)}^{2}} \left(\sum_{m=1}^{{N}_{\theta }}{A}_{jm}^{\theta \left(1\right)} {{\phi }_{\theta }}_{im}\right)-\frac{{A}_{12}cos\alpha }{r(x)} \left(\sum_{n=1}^{{N}_{x}}{A}_{in}^{x(1)} {W}_{nj}\right)\left(\sum_{n=1}^{{N}_{x}}{A}_{in}^{x(1)} {W}_{nj}\right)-\frac{{A}_{22}cos\alpha }{2{r(x)}^{3}} \left(\sum_{m=1}^{{N}_{\theta }}{A}_{jm}^{\theta \left(1\right)} {W}_{im}\right)\left(\sum_{m=1}^{{N}_{\theta }}{A}_{jm}^{\theta \left(1\right)} {W}_{im}\right)-\frac{{A}_{15}^{e}}{r(x)}\left(\sum_{n=1}^{{N}_{x}}\sum_{m=1}^{{N}_{y}}{A}_{in}^{x(1)}{A}_{jm}^{\theta (1)} {\Phi }_{nm}\right)-\frac{{A}_{32}^{e}cos\alpha }{r(x)}\left({\Phi }_{ij}\right)-\frac{{A}_{15}^{m}}{r(x)}\left(\sum_{n=1}^{{N}_{x}}\sum_{m=1}^{{N}_{y}}{A}_{in}^{x(1)}{A}_{jm}^{\theta (1)} {\Psi }_{nm}\right)-\frac{{A}_{32}^{m}cos\alpha }{r(x)}\left({\Psi }_{ij}\right) ={-I}_{0}{\omega }^{2}{W}_{ij}$$

(52c)

$${B}_{11}\left(\sum_{n=1}^{{N}_{x}}{A}_{in}^{x(2)} {U}_{nj}\right)+\frac{{B}_{44}}{{r(x)}^{2}}\left(\sum_{m=1}^{{N}_{\theta }}{A}_{jm}^{\theta \left(2\right)} {U}_{im}\right)+\frac{{B}_{11}sin\alpha }{r(x)}\left(\sum_{n=1}^{{N}_{x}}{A}_{in}^{x(1)} {U}_{nj}\right)-{B}_{22}\frac{{sin}^{2}\alpha }{{r\left(x\right)}^{2}}\left({U}_{ij}\right)-\frac{\left({B}_{22}+{B}_{44}\right)sin\alpha }{{r\left(x\right)}^{2}}\left(\sum_{m=1}^{{N}_{\theta }}{A}_{jm}^{\theta \left(1\right)} {V}_{im}\right)+\frac{\left({B}_{12}+{B}_{44}\right)}{r\left(x\right)}\left(\sum_{n=1}^{{N}_{x}}\sum_{m=1}^{{N}_{y}}{A}_{in}^{x(1)}{A}_{jm}^{\theta (1)} {V}_{nm}\right)+{B}_{12}\frac{cos\alpha }{r\left(x\right)}\left(\sum_{n=1}^{{N}_{x}}{A}_{in}^{x(1)} {W}_{nj}\right)-{A}_{66}\left(\sum_{n=1}^{{N}_{x}}{A}_{in}^{x(1)} {W}_{nj}\right)-\frac{{B}_{22}\mathrm{sin}\alpha \mathrm{cos}\alpha }{{r\left(x\right)}^{2}}\left({W}_{ij}\right)+{D}_{11}\left(\sum_{n=1}^{{N}_{x}}{A}_{in}^{x(1)} {{\phi }_{x}}_{nj}\right)+\frac{{D}_{44}}{{r\left(x\right)}^{2}}\left(\sum_{m=1}^{{N}_{\theta }}{A}_{jm}^{\theta \left(2\right)} {{\phi }_{x}}_{im}\right)+\frac{{D}_{11}\mathrm{sin}\alpha }{r\left(x\right)}\left(\sum_{n=1}^{{N}_{x}}{A}_{in}^{x(1)} {{\phi }_{x}}_{nj}\right)-\frac{{D}_{22}{sin}^{2}\alpha }{{r\left(x\right)}^{2}}\left({{\phi }_{x}}_{ij}\right)-{A}_{66}\left({{\phi }_{x}}_{ij}\right)-\frac{\left({D}_{44}+{D}_{22}\right)sin\alpha }{{r\left(x\right)}^{2}}\left(\sum_{m=1}^{{N}_{\theta }}{A}_{jm}^{\theta \left(1\right)} {{\phi }_{\theta }}_{im}\right)+\frac{\left({D}_{12}+{D}_{44}\right)}{r\left(x\right)}\left(\sum_{n=1}^{{N}_{x}}\sum_{m=1}^{{N}_{y}}{A}_{in}^{x(1)}{A}_{jm}^{\theta (1)} {{\phi }_{\theta }}_{nm}\right)+{B}_{11}\left(\sum_{n=1}^{{N}_{x}}{A}_{in}^{x(2)} {W}_{nj}\right)\left(\sum_{n=1}^{{N}_{x}}{A}_{in}^{x(1)} {W}_{nj}\right)-\frac{{B}_{22}sin\alpha }{{2r\left(x\right)}^{3}}\left(\sum_{m=1}^{{N}_{\theta }}{A}_{jm}^{\theta \left(1\right)} {W}_{im}\right)\left(\sum_{m=1}^{{N}_{\theta }}{A}_{jm}^{\theta \left(1\right)} {W}_{im}\right)+\frac{\left({B}_{11}-{B}_{12}\right)\mathrm{sin}\alpha }{2r\left(x\right)}\left(\sum_{n=1}^{{N}_{x}}{A}_{in}^{x(1)} {W}_{nj}\right)\left(\sum_{n=1}^{{N}_{x}}{A}_{in}^{x(1)} {W}_{nj}\right)+\frac{\left({B}_{12}+{B}_{44}\right)}{{r\left(x\right)}^{2}}\left(\sum_{n=1}^{{N}_{x}}\sum_{m=1}^{{N}_{y}}{A}_{in}^{x(1)}{A}_{jm}^{\theta (1)} {W}_{nm}\right)\left(\sum_{m=1}^{{N}_{\theta }}{A}_{jm}^{\theta \left(1\right)} {W}_{im}\right)+\frac{{B}_{44}}{{r\left(x\right)}^{2}}\left(\sum_{m=1}^{{N}_{\theta }}{A}_{jm}^{\theta \left(2\right)} {W}_{im}\right)\left(\sum_{m=1}^{{N}_{\theta }}{A}_{jm}^{\theta \left(1\right)} {W}_{im}\right)-{B}_{31}^{e}\left(\sum_{n=1}^{{N}_{x}}{A}_{in}^{x(1)} {\Phi }_{nj}\right)-\frac{{B}_{24}^{e}}{r\left(x\right)}\left(\sum_{m=1}^{{N}_{\theta }}{A}_{jm}^{\theta \left(1\right)} {\Phi }_{im}\right)-{B}_{31}^{e}\frac{sin\alpha }{r\left(x\right)}\left({\Phi }_{ij}\right)+{B}_{32}^{e}\frac{sin\alpha }{r\left(x\right)}\left({\Phi }_{ij}\right)-{B}_{31}^{m}\left(\sum_{n=1}^{{N}_{x}}{A}_{in}^{x(1)} {\Psi }_{in}\right)-\frac{{B}_{24}^{m}}{r\left(x\right)}\left(\sum_{m=1}^{{N}_{\theta }}{A}_{jm}^{\theta \left(1\right)} {\Psi }_{im}\right)-{B}_{31}^{m}\frac{sin\alpha }{r\left(x\right)}\left({\Psi }_{ij}\right)+{B}_{32}^{m}\frac{sin\alpha }{r\left(x\right)}\left({\Psi }_{ij}\right)=-{\omega }^{2}\left({I}_{1}{U}_{ij}+{I}_{2}{{\phi }_{x}}_{ij}\right)$$

(52d)

$$\frac{\left({B}_{44}+{B}_{12}\right)}{r(x)}\left(\sum_{n=1}^{{N}_{x}}\sum_{m=1}^{{N}_{y}}{A}_{in}^{x(1)}{A}_{jm}^{\theta (1)} {U}_{nm}\right)+\frac{\left({B}_{44}+{B}_{22}\right)sin\alpha }{{r(x)}^{2}}\left(\sum_{m=1}^{{N}_{\theta }}{A}_{jm}^{\theta \left(1\right)} {\mathrm{U}}_{im}\right)+{B}_{44}\left(\sum_{n=1}^{{N}_{x}}{A}_{in}^{x(2)} {\mathrm{V}}_{in}\right)+\frac{{B}_{22}}{{r(x)}^{2}}\left(\sum_{m=1}^{{N}_{\theta }}{A}_{jm}^{\theta \left(2\right)} {\mathrm{V}}_{im}\right)+\frac{{B}_{44}\mathrm{sin}\alpha }{r(x)}\left(\sum_{n=1}^{{N}_{x}}{A}_{in}^{x(1)} {\mathrm{V}}_{in}\right)+\frac{{A}_{55}\mathrm{cos}\alpha }{r(x)}\left(\sum_{n=1}^{{N}_{x}}{A}_{in}^{x(1)} {\mathrm{V}}_{in}\right)+\frac{{B}_{22}\mathrm{cos}\alpha }{{r(x)}^{2}}\left(\sum_{m=1}^{{N}_{\theta }}{A}_{jm}^{\theta \left(1\right)} {\mathrm{W}}_{im}\right)-\frac{{A}_{55}}{r\left(x\right)}\left(\sum_{m=1}^{{N}_{\theta }}{A}_{jm}^{\theta \left(1\right)} {\mathrm{W}}_{im}\right)+\frac{\left({D}_{44}+{D}_{12}\right)}{r\left(x\right)}\left(\sum_{n=1}^{{N}_{x}}\sum_{m=1}^{{N}_{y}}{A}_{in}^{x(1)}{A}_{jm}^{\theta (1)} {{\phi }_{x}}_{nm}\right)+\frac{\left({D}_{22}+{D}_{44}\right)\mathrm{sin}\alpha }{{r\left(x\right)}^{2}}\left(\sum_{m=1}^{{N}_{\theta }}{A}_{jm}^{\theta \left(1\right)} {{\phi }_{x}}_{im}\right)+{D}_{44}\left(\sum_{n=1}^{{N}_{x}}{A}_{in}^{x(2)} {{\phi }_{\theta }}_{in}\right)+\frac{{D}_{22}}{{r\left(x\right)}^{2}}\left(\sum_{m=1}^{{N}_{\theta }}{A}_{jm}^{\theta \left(2\right)} {{\phi }_{\theta }}_{im}\right)+\frac{{D}_{44}sin\alpha }{r\left(x\right)}\left(\sum_{n=1}^{{N}_{x}}{A}_{in}^{x(1)} {{\phi }_{\theta }}_{in}\right)-\frac{{D}_{44}{sin}^{2}\alpha }{{r\left(x\right)}^{2}}\left({{\phi }_{\theta }}_{ij}\right)-{A}_{55}\left({{\phi }_{\theta }}_{ij}\right)+\frac{{B}_{44}}{r\left(x\right)}\left(\sum_{n=1}^{{N}_{x}}{A}_{in}^{x(2)} {\mathrm{W}}_{in}\right)\left(\sum_{m=1}^{{N}_{\theta }}{A}_{jm}^{\theta \left(1\right)} {\mathrm{W}}_{im}\right)+\frac{{B}_{22}}{{r\left(x\right)}^{3}}\left(\sum_{m=1}^{{N}_{\theta }}{A}_{jm}^{\theta \left(2\right)} {\mathrm{W}}_{im}\right)\left(\sum_{m=1}^{{N}_{\theta }}{A}_{jm}^{\theta \left(1\right)} {\mathrm{W}}_{im}\right)+\frac{\left({B}_{44}+{B}_{12}\right)}{r\left(x\right)}\left(\sum_{n=1}^{{N}_{x}}\sum_{m=1}^{{N}_{y}}{A}_{in}^{x(1)}{A}_{jm}^{\theta (1)} {W}_{nm}\right)\left(\sum_{n=1}^{{N}_{x}}{A}_{in}^{x(1)} {\mathrm{W}}_{in}\right)+\frac{{B}_{44}sin\alpha }{{r\left(x\right)}^{2}}\left(\sum_{n=1}^{{N}_{x}}{A}_{in}^{x(1)} {\mathrm{W}}_{in}\right)\left(\sum_{m=1}^{{N}_{\theta }}{A}_{jm}^{\theta \left(1\right)} {\mathrm{W}}_{im}\right)-{B}_{24}^{e}\left(\sum_{n=1}^{{N}_{x}}{A}_{in}^{x(1)} {\Phi }_{in}\right)-\frac{{B}_{32}^{e}}{r\left(x\right)}\left({\Phi }_{ij}\right)-\frac{2{B}_{24}^{e}sin\alpha }{r\left(x\right)}\left({\Phi }_{ij}\right)+{A}_{15}^{e}\left(\sum_{n=1}^{{N}_{x}}{A}_{in}^{x(2)} {\Phi }_{in}\right)-{B}_{24}^{m}\left(\sum_{n=1}^{{N}_{x}}{A}_{in}^{x(1)} {\Psi }_{in}\right)-\frac{{B}_{32}^{m}}{r\left(x\right)}\left({\Psi }_{ij}\right)-\frac{2{B}_{24}^{m}sin\alpha }{r\left(x\right)}\left({\Psi }_{ij}\right)+{A}_{15}^{e}\left(\sum_{n=1}^{{N}_{x}}{A}_{in}^{x(1)} {\Psi }_{in}\right)=-{\omega }^{2}\left({I}_{1}{V}_{ij}+{I}_{2}{{\phi }_{\theta }}_{ij}\right)$$

(52e)

$${-A}_{31}^{e}\left(\sum_{n=1}^{{N}_{x}}{A}_{in}^{x(1)} {\mathrm{U}}_{in}\right)-\frac{{A}_{32}^{e}sin\alpha }{r\left(x\right)}\left({U}_{ij}\right)-\frac{{A}_{32}^{e}}{r\left(x\right)}\left(\sum_{m=1}^{{N}_{\theta }}{A}_{jm}^{\theta \left(1\right)} {\mathrm{V}}_{im}\right)-\frac{{A}_{32}^{e}cos\alpha }{r\left(x\right)}\left({W}_{ij}\right)-{B}_{31}^{e}\left(\sum_{n=1}^{{N}_{x}}{A}_{in}^{x(1)} {{\phi }_{x}}_{in}\right)-\frac{{B}_{32}^{e}sin\alpha }{r\left(x\right)}\left({{\phi }_{x}}_{ij}\right)-\frac{{B}_{32}^{e}}{r\left(x\right)}\left(\sum_{m=1}^{{N}_{\theta }}{A}_{jm}^{\theta \left(1\right)} {{\phi }_{\theta }}_{im}\right)-{A}_{31}^{e}\frac{1}{2}\left(\sum_{n=1}^{{N}_{x}}{A}_{in}^{x(1)} {W}_{in}\right)\left(\sum_{n=1}^{{N}_{x}}{A}_{in}^{x(1)} {W}_{in}\right)-\frac{{A}_{32}^{e}}{2{r\left(x\right)}^{2}}\left(\sum_{m=1}^{{N}_{\theta }}{A}_{jm}^{\theta \left(1\right)} {\mathrm{W}}_{im}\right)\left(\sum_{m=1}^{{N}_{\theta }}{A}_{jm}^{\theta \left(1\right)} {\mathrm{W}}_{im}\right)+{\widetilde{\kappa }}_{11}\left(\sum_{n=1}^{{N}_{x}}{A}_{in}^{x(2)} {\Phi }_{in}\right)+{\widetilde{\kappa }}_{22}\left(\sum_{m=1}^{{N}_{\theta }}{A}_{jm}^{\theta \left(2\right)} {\Phi }_{im}\right)-{\widetilde{\kappa }}_{33}\left({\Phi }_{ij}\right)+{\widetilde{\lambda }}_{11}\left(\sum_{n=1}^{{N}_{x}}{A}_{in}^{x(2)} {\Psi }_{in}\right)+{\widetilde{\lambda }}_{22}\left(\sum_{m=1}^{{N}_{\theta }}{A}_{jm}^{\theta \left(2\right)} {\Psi }_{im}\right)-{\widetilde{\lambda }}_{33}\left({\Psi }_{ij}\right)=0$$

(52f)

$${-A}_{31}^{m}\left(\sum_{n=1}^{{N}_{x}}{A}_{in}^{x(1)} {\mathrm{U}}_{in}\right)-\frac{{A}_{32}^{m}sin\alpha }{r\left(x\right)}\left({U}_{ij}\right)-\frac{{A}_{32}^{m}}{r\left(x\right)}\left(\sum_{m=1}^{{N}_{\theta }}{A}_{jm}^{\theta \left(1\right)} {\mathrm{V}}_{im}\right)-\frac{{A}_{32}^{m}cos\alpha }{r\left(x\right)}\left({W}_{ij}\right)-{B}_{31}^{m}\left(\sum_{n=1}^{{N}_{x}}{A}_{in}^{x(1)} {{\phi }_{x}}_{in}\right)-\frac{{B}_{32}^{m}sin\alpha }{r\left(x\right)}\left({{\phi }_{x}}_{ij}\right)-\frac{{B}_{32}^{m}}{r\left(x\right)}\left(\sum_{m=1}^{{N}_{\theta }}{A}_{jm}^{\theta \left(1\right)} {{\phi }_{\theta }}_{im}\right)-{A}_{31}^{m}\frac{1}{2}\left(\sum_{n=1}^{{N}_{x}}{A}_{in}^{x(1)} {W}_{in}\right)\left(\sum_{n=1}^{{N}_{x}}{A}_{in}^{x(1)} {W}_{in}\right)-\frac{{A}_{32}^{m}}{2{r\left(x\right)}^{2}}\left(\sum_{m=1}^{{N}_{\theta }}{A}_{jm}^{\theta \left(1\right)} {\mathrm{W}}_{im}\right)\left(\sum_{m=1}^{{N}_{\theta }}{A}_{jm}^{\theta \left(1\right)} {\mathrm{W}}_{im}\right)+{\widetilde{\lambda }}_{11}\left(\sum_{n=1}^{{N}_{x}}{A}_{in}^{x(2)} {\Phi }_{in}\right)+{\widetilde{\lambda }}_{22}\left(\sum_{m=1}^{{N}_{\theta }}{A}_{jm}^{\theta \left(2\right)} {\Phi }_{im}\right)-{\widetilde{\lambda }}_{33}\left({\Phi }_{ij}\right)+{\widetilde{\mu }}_{11}\left(\sum_{n=1}^{{N}_{x}}{A}_{in}^{x(2)} {\Psi }_{in}\right)+{\widetilde{\mu }}_{22}\left(\sum_{m=1}^{{N}_{\theta }}{A}_{jm}^{\theta \left(2\right)} {\Psi }_{im}\right)-{\widetilde{\mu }}_{33}\left({\Psi }_{ij}\right)=0$$

(52g)

The superscripts (1) and (2) in the weight coefficients of the above equations indicate the estimation of the first and second derivatives of the functions. In the following, it is used to convert the above equations into a matrix form by using the concept of double multiplication of Kronecker and Hadamard. By using these two types of multiplication, the nonlinear coupled equations are expressed as follows:

$${A}_{11}\left(\overleftrightarrow{{I}^{\theta }}\otimes \overleftrightarrow{{A}^{x(2)}}\right)\overrightarrow{U}+{A}_{11}sin\alpha \left(\overrightarrow{{I}^{\theta }}\otimes \overleftrightarrow{{a}_{1}}\overleftrightarrow{{A}^{x(1)}}\right)\overrightarrow{U}-{A}_{22}{sin}^{2}\alpha \left(\overleftrightarrow{{I}^{\theta }}\otimes \overleftrightarrow{{a}_{2}}\right)\overrightarrow{U}+{A}_{44}\left(\overleftrightarrow{{A}^{\theta (2)}}\otimes \overleftrightarrow{{a}_{2}}\right)\overline{U }-\left({A}_{44}+{A}_{22}\right)sin\alpha \left(\overleftrightarrow{{A}^{\theta (1)}}\otimes \overleftrightarrow{{a}_{2}}\right)\overrightarrow{V}+\left({A}_{12}+{A}_{44}\right)\left(\overleftrightarrow{{A}^{\theta (1)}}\otimes \overleftrightarrow{{a}_{1}}\overleftrightarrow{{A}^{x(1)}}\right)\overrightarrow{V}+{A}_{12}cos\alpha \left(\overleftrightarrow{{I}^{\theta }}\otimes \overleftrightarrow{{a}_{1}}\overleftrightarrow{{A}^{x(1)}}\right)\overrightarrow{W}-{A}_{12}sin\alpha cos\alpha \left(\overleftrightarrow{{I}^{\theta }}\otimes \overleftrightarrow{{a}_{2}}\right)\overrightarrow{W}+{B}_{11}\left(\overleftrightarrow{{I}^{\theta }}\otimes \overleftrightarrow{{A}^{x(2)}}\right){\overrightarrow{\phi }}_{x}+{B}_{11}sin\alpha \left(\overleftrightarrow{{I}^{\theta }}\otimes \overleftrightarrow{{a}_{1}}\overleftrightarrow{{A}^{x(2)}}\right){\overrightarrow{\phi }}_{x}+{B}_{44}\left(\overleftrightarrow{{A}^{\theta (2)}}\otimes \overleftrightarrow{{a}_{2}}\right){\overline{\phi }}_{x}-{B}_{22}{sin}^{2}\alpha \left(\overleftrightarrow{{I}^{\theta }}\otimes \overleftrightarrow{{a}_{2}}\right){\overrightarrow{\phi }}_{x}-\left({B}_{44}+{B}_{22}\right)sin\alpha \left(\overleftrightarrow{{A}^{\theta (1)}}\otimes \overleftrightarrow{{a}_{2}}\right){\overrightarrow{\phi }}_{\theta }+\left({B}_{12}+{B}_{44}\right)\left(\overleftrightarrow{{A}^{\theta (1)}}\otimes \overleftrightarrow{{a}_{1}}\overleftrightarrow{{A}^{x(1)}}\right){\overrightarrow{\phi }}_{\theta }+{A}_{11}\left[\left(\overleftrightarrow{{I}^{\theta }}\otimes {a}_{1}\overleftrightarrow{{A}^{x(2)}}\right)\overrightarrow{W}\mathrm{o}\left(\overleftrightarrow{{I}^{\theta }}\otimes \overleftrightarrow{{A}^{x(1)}}\right)\overrightarrow{W}\right]+0.5\left({A}_{11}-{A}_{12}\right)sin\alpha \left[\left(\overleftrightarrow{{I}^{\theta }}\otimes \overleftrightarrow{{a}_{1}}\overleftrightarrow{{A}^{x(1)}}\right)\overrightarrow{W}\mathrm{o}\left(\overleftrightarrow{{I}^{\theta }}\otimes \overleftrightarrow{{A}^{x(1)}}\right)\overrightarrow{W}\right]+{A}_{44}\left[\left(\overleftrightarrow{{A}^{\theta (2)}}\otimes \overleftrightarrow{{a}_{2}}\right)\overrightarrow{W}\mathrm{o}\left(\overleftrightarrow{{I}^{\theta }}\otimes \overleftrightarrow{{A}^{x(1)}}\right)\overrightarrow{W}\right]-{A}_{12}sin\alpha \left[\left(\overleftrightarrow{{A}^{\theta (1)}}\otimes \overleftrightarrow{{a}_{3}}\right)\overrightarrow{W}\mathrm{o}\left(\overleftrightarrow{{I}^{\theta }}\otimes \overleftrightarrow{{A}^{x(1)}}\right)\overrightarrow{W}\right]-0.5\left({A}_{12}-{A}_{22}\right)sin\alpha \left[\left(\overleftrightarrow{{A}^{\theta (1)}}\otimes \overleftrightarrow{{a}_{3}}\right)\overrightarrow{W}\mathrm{o}\left(\overleftrightarrow{{A}^{\theta (1)}}\otimes \overleftrightarrow{{I}^{x}}\right)\overrightarrow{W}\right]+\left({A}_{12}+{A}_{44}\right)\left[\left(\overleftrightarrow{{A}^{\theta (1)}}\otimes \overleftrightarrow{{a}_{2}}\overleftrightarrow{{A}^{x(1)}}\right)\overrightarrow{W}\mathrm{o}\left(\overleftrightarrow{{A}^{\theta (1)}}\otimes \overleftrightarrow{{I}^{x}}\right)\overrightarrow{W}\right]-{A}_{31}^{e}\left(\overleftrightarrow{{I}^{\theta }}\otimes \overleftrightarrow{{A}^{x(1)}}\right)\overrightarrow{\Phi }-{A}_{24}^{e}\left(\overleftrightarrow{{A}^{\theta (2)}}\otimes \overleftrightarrow{{a}_{1}}\right)\overrightarrow{\Phi }+\left(-{A}_{31}^{e}+{A}_{32}^{e}\right)\left(\overleftrightarrow{{I}^{\theta }}\otimes \overleftrightarrow{{a}_{1}}\right)\overrightarrow{\Phi } -{A}_{31}^{m}\left(\overleftrightarrow{{I}^{\theta }}\otimes \overleftrightarrow{{A}^{x(1)}}\right)\overrightarrow{\Psi }-{A}_{24}^{m}\left(\overleftrightarrow{{A}^{\theta (2)}}\otimes \overleftrightarrow{{a}_{1}}\right)\overrightarrow{\Psi }+\left(-{A}_{31}^{m}+{A}_{32}^{m}\right)\left(\overleftrightarrow{{I}^{\theta }}\otimes \overleftrightarrow{{a}_{1}}\right)\overrightarrow{\Psi }=-{\omega }^{2}\left[{I}_{0}\left(\overleftrightarrow{{I}^{\theta }}\otimes \overleftrightarrow{{I}^{x}}\right)\overrightarrow{U}+{I}_{1}\left(\overleftrightarrow{{I}^{\theta }}\otimes \overleftrightarrow{{I}^{x}}\right){\overrightarrow{\phi }}_{x}\right]$$

(53a)

$$\left({A}_{22}+{A}_{44}\right)sin\alpha \left(\overleftrightarrow{{A}^{\theta (1)}}\otimes \overleftrightarrow{{a}_{2}}\right)\overrightarrow{U}+\left({A}_{12}+{A}_{44}\right)\left(\overleftrightarrow{{A}^{\theta (1)}}\otimes \overleftrightarrow{{a}_{1}}\overleftrightarrow{{A}^{x(1)}}\right)\overrightarrow{U}+{A}_{44}\left(\overleftrightarrow{{I}^{\theta }}\otimes \overleftrightarrow{{A}^{x(2)}}\right)\overrightarrow{V}+{A}_{22}\left(\overleftrightarrow{{A}^{\theta (2)}}\otimes \overleftrightarrow{{a}_{2}}\right)\overrightarrow{V}+{A}_{44}sin\alpha \left(\overleftrightarrow{{I}^{\theta }}\otimes \overleftrightarrow{{a}_{1}}\overleftrightarrow{{A}^{x(1)}}\right)\overrightarrow{V}-{A}_{44}{sin}^{2}\alpha \left(\overleftrightarrow{{I}^{\theta }}\otimes \overleftrightarrow{{a}_{2}}\right)\overrightarrow{V}-{A}_{55}{cos}^{2}\alpha \left(\overleftrightarrow{{I}^{\theta }}\otimes \overleftrightarrow{{a}_{2}}\right)\overrightarrow{V}+\left({A}_{22}+{A}_{55}\right)cos\alpha \left(\overleftrightarrow{{A}^{\theta (1)}}\otimes \overleftrightarrow{{a}_{2}}\right)\overrightarrow{W}+\left({B}_{22}+{B}_{44}\right)sin\alpha \left(\overleftrightarrow{{A}^{\theta (1)}}\otimes \overleftrightarrow{{a}_{2}}\right){\overrightarrow{\phi }}_{x}+\left({B}_{12}+{B}_{44}\right)\left(\overleftrightarrow{{A}^{\theta (1)}}\otimes \overleftrightarrow{{a}_{1}}\overleftrightarrow{{A}^{x}}\right){\overrightarrow{\phi }}_{x}+{B}_{44}\left(\overleftrightarrow{{I}^{\theta }}\otimes \overleftrightarrow{{A}^{x(1)}}\right){\overrightarrow{\phi }}_{\theta }+{B}_{22}\left(\overleftrightarrow{{A}^{\theta (2)}}\otimes \overleftrightarrow{{a}_{2}}\right){\overrightarrow{\phi }}_{\theta }+{B}_{44}sin\alpha \left(\overleftrightarrow{{I}^{\theta }}\otimes \overleftrightarrow{{a}_{1}}\overleftrightarrow{{A}^{x(1)}}\right){\overrightarrow{\phi }}_{\theta }-{B}_{44}{sin}^{2}\alpha \left(\overleftrightarrow{{I}^{\theta }}\otimes \overleftrightarrow{{a}_{2}}\right){\overrightarrow{\phi }}_{\theta }+{A}_{55}cos\alpha \left(\overleftrightarrow{{I}^{\theta }}\otimes \overleftrightarrow{{a}_{1}}\right){\overrightarrow{\phi }}_{\theta }+{A}_{44}\left[\left(\overleftrightarrow{{I}^{\theta }}\otimes \overleftrightarrow{{a}_{1}}\overleftrightarrow{{A}^{x(2)}}\right)\overrightarrow{W}\mathrm{o}\left(\overleftrightarrow{{A}^{\theta (1)}}\otimes \overleftrightarrow{{I}^{x}}\right)\overrightarrow{W}\right]+{A}_{44}sin\alpha \left[\left(\overleftrightarrow{{I}^{\theta }}\otimes \overleftrightarrow{{a}_{2}}\overleftrightarrow{{A}^{x(1)}}\right)\overleftrightarrow{W}\mathrm{o}\left(\overleftrightarrow{{A}^{\theta (1)}}\otimes \overleftrightarrow{{I}^{x}}\right)\overrightarrow{W}\right]+{A}_{22}\left[\left(\overleftrightarrow{{A}^{\theta (1)}}\otimes \overleftrightarrow{{a}_{3}}\right)\overrightarrow{W}\mathrm{o}\left(\overleftrightarrow{{A}^{\theta (1)}}\otimes \overleftrightarrow{{I}^{x}}\right)\overrightarrow{W}\right]+\left({A}_{44}+{A}_{12}\right)\left[\left(\overleftrightarrow{{A}^{\theta (1)}}\otimes \overleftrightarrow{{a}_{1}}\overleftrightarrow{{A}^{x(1)}}\right)\overrightarrow{W}\mathrm{o}\left(\overleftrightarrow{{I}^{\theta }}\otimes \overleftrightarrow{{A}^{x(1)}}\right)\overline{W }\right]-{A}_{32}^{e}\left(\overleftrightarrow{{A}^{\theta (1)}}\otimes \overleftrightarrow{{a}_{1}}\right)\overrightarrow{\Phi }-{A}_{24}^{e}\left(\overleftrightarrow{{A}^{\theta (1)}}\otimes \overleftrightarrow{{A}^{x(1)}}\right)\overrightarrow{\Phi }-2{A}_{24}^{e}sin\alpha \left(\overleftrightarrow{{A}^{\theta (1)}}\otimes \overleftrightarrow{{a}_{1}}\right)\overrightarrow{\Phi }-{A}_{15}^{e}cos\alpha \left(\overleftrightarrow{{I}^{\theta }}\otimes \overleftrightarrow{{a}_{1}}\overleftrightarrow{{A}^{x(1)}}\right)\overrightarrow{\Phi }-{A}_{32}^{m}\left(\overleftrightarrow{{A}^{\theta (1)}}\otimes \overleftrightarrow{{a}_{1}}\right)\overrightarrow{\Psi }-{A}_{24}^{m}\left(\overleftrightarrow{{A}^{\theta (1)}}\otimes \overleftrightarrow{{A}^{x(1)}}\right)\overrightarrow{\Psi }-2{A}_{24}^{m}sin\alpha \left(\overleftrightarrow{{A}^{\theta (1)}}\otimes \overleftrightarrow{{a}_{1}}\right)\overrightarrow{\Psi }-{A}_{15}^{m}cos\alpha \left(\overleftrightarrow{{I}^{\theta }}\otimes \overleftrightarrow{{a}_{1}}\overleftrightarrow{{A}^{x(1)}}\right)\overrightarrow{\Psi }=-{\omega }^{2}\left[{I}_{0}\left(\overleftrightarrow{{I}^{\theta }}\otimes \overleftrightarrow{{I}^{x}}\right)\overrightarrow{V}+{I}_{1}\left(\overleftrightarrow{{I}^{\theta }}\otimes \overleftrightarrow{{I}^{x}}\right){\overrightarrow{\phi }}_{\theta }\right]$$

(53b)

$$-{A}_{12}cos\alpha \left(\overleftrightarrow{{I}^{\theta }}\otimes \overleftrightarrow{{a}_{1}}\overleftrightarrow{{A}^{x(1)}}\right)\overrightarrow{U}-{A}_{22}sin\alpha cos\alpha \left(\overleftrightarrow{{I}^{\theta }}\otimes \overleftrightarrow{{a}_{2}}\right)\overrightarrow{U}-{A}_{22}cos\alpha \left(\overleftrightarrow{{A}^{\theta (1)}}\otimes \overleftrightarrow{{a}_{2}}\right)\overrightarrow{V}-{A}_{55}cos\alpha \left(\overleftrightarrow{{A}^{\theta \left(1\right)}}\otimes \overleftrightarrow{{a}_{2}}\right)+{A}_{66}\left(\overleftrightarrow{{I}^{\theta }}\otimes \overleftrightarrow{{A}^{x(1)}}\right)\overrightarrow{W}-{A}_{66}sin\alpha \left(\overleftrightarrow{{I}^{\theta }}\otimes \overleftrightarrow{{a}_{1}}\overleftrightarrow{{A}^{x}}\right)\overrightarrow{W}+{A}_{55}\left(\overleftrightarrow{{A}^{\theta (2)}}\otimes \overleftrightarrow{{a}_{2}}\right)\overrightarrow{W}-{A}_{22}{cos}^{2}\alpha \left(\overleftrightarrow{{I}^{\theta }}\otimes \overleftrightarrow{{a}_{2}}\right)\overrightarrow{W}+{A}_{66}\left(\overleftrightarrow{{I}^{\theta }}\otimes \overleftrightarrow{{A}^{x(1)}}\right){\overrightarrow{\phi }}_{x}-{B}_{12}cos\alpha \left(\overleftrightarrow{{I}^{\theta }}\otimes \overleftrightarrow{{a}_{1}}\overleftrightarrow{{A}^{x(1)}}\right){\overrightarrow{\phi }}_{x}-{A}_{66}sin\alpha \left(\overleftrightarrow{{I}^{\theta }}\otimes \overleftrightarrow{{a}_{1}}\right){\overrightarrow{\phi }}_{x}-{B}_{22}sin\alpha cos\alpha \left(\overleftrightarrow{{I}^{\theta }}\otimes \overleftrightarrow{{a}_{2}}\right){\overrightarrow{\phi }}_{x}+{A}_{55}\left(\overleftrightarrow{{A}^{\theta (1)}}\otimes \overleftrightarrow{{a}_{1}}\right){\overrightarrow{\phi }}_{\theta }-{B}_{22}cos\alpha \left(\overleftrightarrow{{A}^{\theta (1)}}\otimes \overleftrightarrow{{a}_{2}}\right){\overrightarrow{\phi }}_{\theta }-0.5{A}_{12}cos\alpha \left[\left(\overleftrightarrow{{I}^{\theta }}\otimes \overleftrightarrow{{a}_{1}}\overleftrightarrow{{A}^{x(1)}}\right)\overrightarrow{W}\mathrm{o}\left(\overleftrightarrow{{I}^{\theta }}\otimes \overleftrightarrow{{A}^{x(1)}}\right)\overrightarrow{W}\right]-0.5{A}_{22}cos\alpha \left[\left(\overleftrightarrow{{A}^{\theta (1)}}\otimes \overleftrightarrow{{a}_{3}}\right)\overrightarrow{W}\mathrm{o}\left(\overleftrightarrow{{A}^{\theta (1)}}\otimes \overleftrightarrow{{I}^{x}}\right)\overrightarrow{W}\right]-{A}_{15}^{e}\left(\overleftrightarrow{{A}^{\theta (1)}}\otimes \overleftrightarrow{{a}_{1}}\overleftrightarrow{{A}^{x(1)}}\right)\overrightarrow{\Phi }-{A}_{32}^{e}cos\alpha \left(\overleftrightarrow{{I}^{\theta }}\otimes \overleftrightarrow{{a}_{1}}\right)\overrightarrow{\Phi }-{A}_{15}^{m}\left(\overleftrightarrow{{A}^{\theta (1)}}\otimes \overleftrightarrow{{a}_{1}}\overleftrightarrow{{A}^{x(1)}}\right)\overrightarrow{\Psi }-{A}_{32}^{m}cos\alpha \left(\overleftrightarrow{{I}^{\theta }}\otimes \overleftrightarrow{{a}_{1}}\right)\overrightarrow{\Psi }=-{\omega }^{2}{I}_{0}\left(\overleftrightarrow{{I}^{\theta }}\otimes \overleftrightarrow{{I}^{x}}\right)\overrightarrow{W}$$

(53c)

$${B}_{11}\left(\overleftrightarrow{{I}^{\theta }}\otimes \overleftrightarrow{{A}^{x(1)}}\right)\overrightarrow{U}+{B}_{44}\left(\overleftrightarrow{{A}^{\theta (2)}}\otimes \overleftrightarrow{{a}_{2}}\right)\overrightarrow{U}+{B}_{11}sin\alpha \left(\overleftrightarrow{{I}^{\theta }}\otimes \overleftrightarrow{{a}_{1}}\overleftrightarrow{{A}^{x(1)}}\right)\overrightarrow{U}-{B}_{22}{sin}^{2}\alpha \left(\overleftrightarrow{{I}^{\theta }}\otimes \overleftrightarrow{{a}_{2}}\right)\overrightarrow{U}-\left({B}_{44}+{B}_{22}\right)sin\alpha \left(\overleftrightarrow{{A}^{\theta (1)}}\otimes \overleftrightarrow{{a}_{2}}\right)\overrightarrow{V}+\left({B}_{12}+{B}_{44}\right)\left(\overleftrightarrow{{A}^{\theta (1)}}\otimes \overleftrightarrow{{a}_{1}}\overleftrightarrow{{A}^{x(1)}}\right)\overrightarrow{V}+{B}_{12}cos\alpha \left(\overleftrightarrow{{I}^{\theta }}\otimes \overleftrightarrow{{a}_{1}}\overleftrightarrow{{A}^{x(1)}}\right)\overrightarrow{W}-{A}_{66}\left(\overleftrightarrow{{I}^{\theta }}\otimes \overleftrightarrow{{A}^{x(1)}}\right)\overrightarrow{W}-{B}_{22}cos\alpha sin\alpha \left(\overleftrightarrow{{I}^{\theta }}\otimes \overleftrightarrow{{a}_{2}}\right)\overrightarrow{W}+{D}_{11}\left(\overleftrightarrow{{I}^{\theta }}\otimes \overleftrightarrow{{A}^{x(2)}}\right){\overrightarrow{\phi }}_{x}+{D}_{44}\left(\overleftrightarrow{{A}^{\theta (2)}}\otimes \overleftrightarrow{{a}_{2}}\right){\overrightarrow{\phi }}_{x}+{D}_{11}sin\alpha \left(\overleftrightarrow{{I}^{\theta }}\otimes \overleftrightarrow{{a}_{1}}\overleftrightarrow{{A}^{x(1)}}\right){\overrightarrow{\phi }}_{x}-{D}_{22}{sin}^{2}\alpha \left(\overleftrightarrow{{I}^{\theta }}\otimes \overleftrightarrow{{a}_{2}}\right){\overrightarrow{\phi }}_{x}-{A}_{66}\left(\overleftrightarrow{{I}^{\theta }}\otimes \overleftrightarrow{{I}^{x}}\right){\overrightarrow{\phi }}_{x}-\left({D}_{44}+{D}_{22}\right)\left(\overleftrightarrow{{A}^{\theta (1)}}\otimes \overleftrightarrow{{a}_{2}}\right){\overrightarrow{\phi }}_{\theta }+\left({D}_{12}+{D}_{44}\right)\left(\overleftrightarrow{{A}^{\theta (1)}}\otimes \overleftrightarrow{{a}_{1}}\overleftrightarrow{{A}^{x(1)}}\right){\overrightarrow{\phi }}_{\theta }+{B}_{11}\left[\left(\overleftrightarrow{{I}^{\theta }}\otimes \overleftrightarrow{{A}^{x(2)}}\right)\overrightarrow{W}\mathrm{o}\left(\overleftrightarrow{{I}^{\theta }}\otimes \overleftrightarrow{{A}^{x(1)}}\right)\overrightarrow{W}\right]+\left({B}_{12}+{B}_{22}\right)0.5sin\alpha \left[\left(\overleftrightarrow{{A}^{\theta (1)}}\otimes \overleftrightarrow{{a}_{3}}\right)\overrightarrow{W}\mathrm{o}\left(\overleftrightarrow{{A}^{\theta (1)}}\otimes \overleftrightarrow{{I}^{x}}\right)\overrightarrow{W}\right]+0.5\left({B}_{11}-{B}_{12}\right)\left[\left(\overleftrightarrow{{I}^{\theta }}\otimes \overleftrightarrow{{a}_{1}}\overleftrightarrow{{A}^{x(1)}}\right)\overrightarrow{W}\mathrm{o}\left(\overleftrightarrow{{I}^{\theta }}\otimes \overleftrightarrow{{A}^{x(1)}}\right)\overrightarrow{W}\right]+\left({B}_{12}+{B}_{44}\right)\left[\left(\overleftrightarrow{{A}^{\theta (1)}}\otimes \overleftrightarrow{{a}_{2}}\overleftrightarrow{{A}^{x(1)}}\right)\overrightarrow{W}\mathrm{o}\left(\overleftrightarrow{{A}^{\theta (1)}}\otimes \overleftrightarrow{{I}^{x}}\right)\overrightarrow{W}\right]+{B}_{44}\left[\left(\overleftrightarrow{{A}^{\theta (2)}}\otimes \overleftrightarrow{{a}_{2}}\right)\overrightarrow{W}\mathrm{o}\left(\overleftrightarrow{{I}^{\theta }}\otimes \overleftrightarrow{{A}^{x(1)}}\right)\overrightarrow{W}\right]+{B}_{31}^{e}\left(\overleftrightarrow{{I}^{\theta }}\otimes \overleftrightarrow{{A}^{x(1)}}\right)\overrightarrow{\Phi }-{B}_{24}^{e}\left(\overleftrightarrow{{A}^{\theta (1)}}\otimes \overleftrightarrow{{a}_{1}}\right)\overrightarrow{\Phi }+\left({B}_{32}^{e}-{B}_{31}^{e}\right)sin\alpha \left(\overleftrightarrow{{I}^{\theta }}\otimes \overleftrightarrow{{a}_{1}}\right)\overrightarrow{\Phi }+{B}_{31}^{m}\left(\overleftrightarrow{{I}^{\theta }}\otimes \overleftrightarrow{{A}^{x(1)}}\right)\overrightarrow{\Psi }-{B}_{24}^{m}\left(\overleftrightarrow{{A}^{\theta (2)}}\otimes \overleftrightarrow{{a}_{1}}\right)\overrightarrow{\Psi }+\left({B}_{32}^{m}-{B}_{31}^{m}\right)sin\alpha \left(\overleftrightarrow{{I}^{\theta }}\otimes \overleftrightarrow{{a}_{1}}\right)\overrightarrow{\Psi }=-{\omega }^{2}\left[{I}_{1}\left(\overleftrightarrow{{I}^{\theta }}\otimes \overleftrightarrow{{I}^{x}}\right)\overrightarrow{U}+{I}_{2}\left(\overleftrightarrow{{I}^{\theta }}\otimes \overleftrightarrow{{I}^{x}}\right){\overrightarrow{\phi }}_{x}\right]$$

(53d)

$$\left({B}_{44}+{B}_{12}\right)]\left(\overleftrightarrow{{A}^{\theta (1)}}\otimes \overleftrightarrow{{a}_{1}}\overleftrightarrow{{A}^{x(1)}}\right)\overrightarrow{U}+\left({B}_{22}+{B}_{44}\right)sin\alpha \left(\overleftrightarrow{{A}^{\theta (1)}}\otimes \overleftrightarrow{{a}_{2}}\right)\overrightarrow{U}+{B}_{44}\left(\overleftrightarrow{{I}^{\theta }}\otimes \overleftrightarrow{{A}^{x(2)}}\right)\overrightarrow{V}+{B}_{22}\left(\overleftrightarrow{{A}^{\theta (2)}}\otimes \overleftrightarrow{{a}_{2}}\right)+{B}_{44}sin\alpha \left(\overleftrightarrow{{I}^{\theta }}\otimes \overleftrightarrow{{a}_{1}}\overleftrightarrow{{A}^{x(1)}}\right)\overrightarrow{V}-{B}_{44}{sin}^{2}\alpha \left(\overleftrightarrow{{I}^{\theta }}\otimes \overleftrightarrow{{a}_{2}}\right)\overrightarrow{V}+{A}_{55}cos\alpha \left(\overleftrightarrow{{I}^{\theta }}\otimes \overleftrightarrow{{a}_{1}}\right)\overrightarrow{V}+{B}_{22}cos\alpha \left(\overleftrightarrow{{A}^{\theta (1)}}\otimes \overleftrightarrow{{a}_{2}}\right)\overrightarrow{W}-{A}_{55}\left(\overleftrightarrow{{A}^{\theta (1)}}\otimes \overleftrightarrow{{a}_{1}}\right)\overrightarrow{W}+\left({D}_{44}+{D}_{12}\right)\left(\overleftrightarrow{{A}^{\theta (1)}}\otimes \overleftrightarrow{{a}_{1}}\overleftrightarrow{{A}^{x(1)}}\right){\overrightarrow{\phi }}_{x}+\left({D}_{22}+{D}_{44}\right)sin\alpha \left(\overleftrightarrow{{A}^{\theta (1)}}\otimes \overleftrightarrow{{a}_{2}}\right){\overrightarrow{\phi }}_{x}+{D}_{44}\left(\overleftrightarrow{{I}^{\theta }}\otimes \overleftrightarrow{{A}^{x(2)}}\right){\overrightarrow{\phi }}_{\theta }+{D}_{22}\left(\overleftrightarrow{{A}^{\theta (2)}}\otimes \overleftrightarrow{{a}_{2}}\right){\overrightarrow{\phi }}_{\theta }+{D}_{44}sin\alpha \left(\overleftrightarrow{{I}^{\theta }}\otimes \overleftrightarrow{{a}_{1}}\overleftrightarrow{{A}^{x(1)}}\right){\overrightarrow{\phi }}_{\theta }-{D}_{44}{sin}^{2}\alpha \left(\overleftrightarrow{{I}^{\theta }}\otimes \overleftrightarrow{{a}_{2}}\right){\overrightarrow{\phi }}_{\theta }-{A}_{55}\left(\overleftrightarrow{{I}^{\theta }}\otimes \overleftrightarrow{{I}^{x}}\right){\overrightarrow{\phi }}_{\theta }+{B}_{44}\left[\left(\overleftrightarrow{{I}^{\theta }}\otimes \overleftrightarrow{{a}_{1}}\overleftrightarrow{{A}^{x(2)}}\right)\overrightarrow{W}\mathrm{o}\left(\overleftrightarrow{{A}^{\theta (1)}}\otimes \overleftrightarrow{{I}^{x}}\right)\overrightarrow{W}\right]+{B}_{22}\left[\left(\overleftrightarrow{{A}^{\theta (2)}}\otimes \overleftrightarrow{{a}_{3}}\right)\overrightarrow{W}\mathrm{o}\left(\overleftrightarrow{{A}^{\theta (1)}}\otimes \overleftrightarrow{{I}^{x}}\right)\overrightarrow{W}\right]+\left({B}_{44}+{B}_{12}\right)\left[\left(\overleftrightarrow{{A}^{\theta (1)}}\otimes \overleftrightarrow{{a}_{1}}\overleftrightarrow{{A}^{x(1)}}\right)\overrightarrow{W}\mathrm{o}\left(\overleftrightarrow{{I}^{\theta }}\otimes \overleftrightarrow{{A}^{x(1)}}\right)\overrightarrow{W}\right]+{B}_{44}sin\alpha \left[\left(\overleftrightarrow{{I}^{\theta }}\otimes \overleftrightarrow{{a}_{2}}\overleftrightarrow{{A}^{x(1)}}\right)\overrightarrow{W}\mathrm{o}\left(\overleftrightarrow{{A}^{\theta (1)}}\otimes \overleftrightarrow{{I}^{x}}\right)\overrightarrow{W}\right]+\left({A}_{15}^{e}-{A}_{24}^{e}\right)\left(\overleftrightarrow{{I}^{\theta }}\otimes \overleftrightarrow{{A}^{x(1)}}\right)\overrightarrow{\Phi }-{B}_{32}^{e}\left(\overleftrightarrow{{I}^{\theta }}\otimes \overleftrightarrow{{a}_{1}}\right)\overrightarrow{\Phi }-2{B}_{24}^{e}sin\alpha \left(\overleftrightarrow{{I}^{\theta }}\otimes \overleftrightarrow{{a}_{1}}\right)\overrightarrow{\Phi } +\left({A}_{15}^{m}-{A}_{24}^{m}\right)\left(\overleftrightarrow{{I}^{\theta }}\otimes \overleftrightarrow{{A}^{x(1)}}\right)\overrightarrow{\Psi }-{B}_{32}^{m}\left(\overleftrightarrow{{I}^{\theta }}\otimes \overleftrightarrow{{a}_{1}}\right)\overrightarrow{\Psi }-2{B}_{24}^{m}sin\alpha \left(\overleftrightarrow{{I}^{\theta }}\otimes \overleftrightarrow{{a}_{1}}\right)\overrightarrow{\Psi }=-{\omega }^{2}\left[{I}_{1}\left(\overleftrightarrow{{I}^{\theta }}\otimes \overleftrightarrow{{I}^{x}}\right)\overrightarrow{V}+{I}_{2}\left(\overleftrightarrow{{I}^{\theta }}\otimes \overleftrightarrow{{I}^{x}}\right){\overrightarrow{\phi }}_{\theta }\right]$$

(53e)

$$-{A}_{31}^{e}\left(\overleftrightarrow{{I}^{\theta }}\otimes \overleftrightarrow{{A}^{x(1)}}\right)\overrightarrow{U}-{A}_{32}^{e}sin\alpha \left(\overleftrightarrow{{I}^{\theta }}\otimes \overleftrightarrow{{a}_{1}}\right)\overrightarrow{U}-{A}_{32}^{e}\left(\overleftrightarrow{{A}^{\theta (1)}}\otimes {a}_{1}\right)\overrightarrow{V}-{A}_{32}^{e}cos\alpha \left(\overleftrightarrow{{I}^{\theta }}\otimes \overleftrightarrow{{a}_{1}}\right)\overrightarrow{W}-{B}_{31}^{e}\left(\overleftrightarrow{{I}^{\theta }}\otimes \overleftrightarrow{{A}^{x(1)}}\right){\overrightarrow{\phi }}_{x}-{B}_{32}^{e}sin\alpha \left(\overleftrightarrow{{I}^{\theta }}\otimes \overleftrightarrow{{a}_{1}}\right){\overrightarrow{\phi }}_{x}-{B}_{32}^{e}\left(\overleftrightarrow{{A}^{\theta (1)}}\otimes \overleftrightarrow{{a}_{1}}\right){\overrightarrow{\phi }}_{\theta }-0.5{A}_{31}^{e}\left[\left(\overleftrightarrow{{I}^{\theta }}\otimes \overleftrightarrow{{A}^{x(1)}}\right)\overrightarrow{W}\mathrm{o}\left(\overleftrightarrow{{I}^{\theta }}\otimes \overleftrightarrow{{A}^{x(1)}}\right)\overrightarrow{W}\right]-0.5{A}_{32}^{e}\left[\left(\overleftrightarrow{{A}^{\theta (1)}}\otimes \overleftrightarrow{{a}_{2}}\right)\overrightarrow{W}\mathrm{o}\left(\overleftrightarrow{{A}^{\theta (1)}}\otimes \overleftrightarrow{{I}^{x}}\right)\overrightarrow{W}\right]+{\widetilde{\kappa }}_{11}\left(\overleftrightarrow{{I}^{\theta }}\otimes \overleftrightarrow{{A}^{x(2)}}\right)\overrightarrow{\Phi }+{\widetilde{\kappa }}_{22}\left(\overleftrightarrow{{A}^{\theta (2)}}\otimes \overleftrightarrow{{I}^{x}}\right)\overrightarrow{\Phi }-{\widetilde{\kappa }}_{33}\left(\overleftrightarrow{{I}^{\theta }}\otimes \overleftrightarrow{{I}^{x}}\right)\overrightarrow{\Phi }+{\widetilde{\lambda }}_{11}\left(\overleftrightarrow{{I}^{\theta }}\otimes \overleftrightarrow{{A}^{x(2)}}\right)\overrightarrow{\Psi }+{\widetilde{\lambda }}_{22}\left(\overleftrightarrow{{A}^{\theta (2)}}\otimes \overleftrightarrow{{I}^{x}}\right)\overrightarrow{\Psi }-{\widetilde{\lambda }}_{33}\left(\overleftrightarrow{{I}^{\theta }}\otimes \overleftrightarrow{{I}^{x}}\right)\overrightarrow{\Psi }=0$$

(53f)

In the above equations, the superscript $\left(\overleftrightarrow{}\right)$ represents the two-dimensional tensor, and the superscript $\left(\overrightarrow{}\right)$ represents the one-dimensional tensor. Further, Eqs. (53a–f) can be expressed in the matrix form of the following nonlinear eigenvalue problem:

$$\overleftrightarrow{K}\overrightarrow{S}={\omega }^{2}\overleftrightarrow{M}\overrightarrow{S} , \overleftrightarrow{K}=\left({\overleftrightarrow{K}}_{L}+{\overleftrightarrow{K}}_{NL}\right)$$

(54)

where ${\overleftrightarrow{K}}_{L}$ is the two-dimensional linear stiffness tensor, and ${\overleftrightarrow{K}}_{NL}$ is the two-dimensional nonlinear stiffness tensor which is a function of $W$, and $\overleftrightarrow{M}$ is the two-dimensional mass tensor that can be expressed as follows:

$${\overleftrightarrow{K}}_{L}=\left[\begin{array}{ccccccc}{\overleftrightarrow{K}}_{L11}&\quad {\overleftrightarrow{K}}_{L12}&\quad {\overleftrightarrow{K}}_{L13}&\quad {\overleftrightarrow{K}}_{L14}&\quad {\overleftrightarrow{K}}_{L15}& \quad{\overleftrightarrow{K}}_{L16}&\quad {\overleftrightarrow{K}}_{L17}\\ {\overleftrightarrow{K}}_{L21}&\quad {\overleftrightarrow{K}}_{L22}&\quad {\overleftrightarrow{K}}_{L23}&\quad {\overleftrightarrow{K}}_{L24}&\quad {\overleftrightarrow{K}}_{L25}&\quad {\overleftrightarrow{K}}_{L26}&\quad {\overleftrightarrow{K}}_{L27}\\ {\overleftrightarrow{K}}_{L31}&\quad {\overleftrightarrow{K}}_{L32}&\quad {\overleftrightarrow{K}}_{L33}&\quad {\overleftrightarrow{K}}_{L34}&\quad {\overleftrightarrow{K}}_{L35}&\quad {\overleftrightarrow{K}}_{L36}&\quad {\overleftrightarrow{K}}_{L37}\\ {\overleftrightarrow{K}}_{L41}&\quad {\overleftrightarrow{K}}_{L42}&\quad {\overleftrightarrow{K}}_{L43}&\quad {\overleftrightarrow{K}}_{L44}&\quad {\overleftrightarrow{K}}_{L45}&\quad {\overleftrightarrow{K}}_{L46}&\quad {\overleftrightarrow{K}}_{L47}\\ {\overleftrightarrow{K}}_{L51}&\quad {\overleftrightarrow{K}}_{L52}&\quad {\overleftrightarrow{K}}_{L53}&\quad {\overleftrightarrow{K}}_{L54}&\quad {\overleftrightarrow{K}}_{L55}&\quad {\overleftrightarrow{K}}_{L56}&\quad {\overleftrightarrow{K}}_{L57}\\ {\overleftrightarrow{K}}_{L61}&\quad {\overleftrightarrow{K}}_{L62}&\quad {\overleftrightarrow{K}}_{L63}&\quad {\overleftrightarrow{K}}_{L64}&\quad {\overleftrightarrow{K}}_{L65}&\quad {\overleftrightarrow{K}}_{L66}&\quad {\overleftrightarrow{K}}_{L67}\\ {\overleftrightarrow{K}}_{L71}&\quad {\overleftrightarrow{K}}_{L72}&\quad {\overleftrightarrow{K}}_{L73}&\quad {\overleftrightarrow{K}}_{L74}&\quad {\overleftrightarrow{K}}_{L75}&\quad {\overleftrightarrow{K}}_{L76}&\quad {\overleftrightarrow{K}}_{L77}\end{array}\right]$$

$${\overleftrightarrow{K}}_{NL} =\left[\begin{array}{ccccccc}\overleftrightarrow{Z}&\quad \overleftrightarrow{Z}&\quad {\overleftrightarrow{K}}_{NL13}&\quad \overleftrightarrow{Z}&\quad \overleftrightarrow{Z}& \overleftrightarrow{Z}&\quad \overleftrightarrow{Z}\\ \overleftrightarrow{Z}&\quad \overleftrightarrow{Z}&\quad {\overleftrightarrow{K}}_{NL23}&\quad \overleftrightarrow{Z}&\quad \overleftrightarrow{Z}&\quad \overleftrightarrow{Z}&\quad \overleftrightarrow{Z}\\ \overleftrightarrow{Z}&\quad \overleftrightarrow{Z}& \quad {\overleftrightarrow{K}}_{NL24}&\quad \overleftrightarrow{Z}&\quad \overleftrightarrow{Z}&\quad \overleftrightarrow{Z}&\quad \overleftrightarrow{Z}\\ \overleftrightarrow{Z}&\quad \overleftrightarrow{Z}&\quad {\overleftrightarrow{K}}_{NL25}&\quad \overleftrightarrow{Z}&\quad \overleftrightarrow{Z}&\quad \overleftrightarrow{Z}&\quad \overleftrightarrow{Z}\\ \overleftrightarrow{Z}&\quad \overleftrightarrow{Z}&\quad {\overleftrightarrow{K}}_{NL26}&\quad \overleftrightarrow{Z}&\quad \overleftrightarrow{Z}&\quad \overleftrightarrow{Z}&\quad \overleftrightarrow{Z}\\ \overleftrightarrow{Z}&\quad \overleftrightarrow{Z}&\quad {\overleftrightarrow{K}}_{NL27}&\quad \overleftrightarrow{Z}&\quad \overleftrightarrow{Z}&\quad \overleftrightarrow{Z}&\quad \overleftrightarrow{Z}\\ \overleftrightarrow{Z}&\quad \overleftrightarrow{Z}&\quad {\overleftrightarrow{K}}_{NL28}&\quad \overleftrightarrow{Z}&\quad \overleftrightarrow{Z}& \overleftrightarrow{Z}&\quad \overleftrightarrow{Z}\end{array}\right]$$

$$\overleftrightarrow{M} =\left[\begin{array}{ccccccc}{\overleftrightarrow{M}}_{11}&\quad \overleftrightarrow{Z}&\quad \overleftrightarrow{Z}&\quad {\overleftrightarrow{M}}_{14}&\quad \overleftrightarrow{Z}&\quad \overleftrightarrow{Z}& \quad\overleftrightarrow{Z}\\ \overleftrightarrow{Z}&\quad {\overleftrightarrow{M}}_{22}&\quad \overleftrightarrow{Z}&\quad \overleftrightarrow{Z}&\quad {\overleftrightarrow{M}}_{25}&\quad \overleftrightarrow{Z}& \overleftrightarrow{Z}\\ \overleftrightarrow{Z}&\quad \overleftrightarrow{Z}&\quad {\overleftrightarrow{M}}_{33}&\quad \overleftrightarrow{Z}&\quad \overleftrightarrow{Z}&\quad \overleftrightarrow{Z}&\quad \overleftrightarrow{Z}\\ {\overleftrightarrow{M}}_{41}&\quad \overleftrightarrow{Z}&\quad \overleftrightarrow{Z}&\quad {\overleftrightarrow{M}}_{44}&\quad \overleftrightarrow{Z}&\quad \overleftrightarrow{Z}&\quad \overleftrightarrow{Z}\\ \overleftrightarrow{Z}&\quad {\overleftrightarrow{M}}_{52}&\quad \overleftrightarrow{Z}&\quad \overleftrightarrow{Z}&\quad {\overleftrightarrow{M}}_{55}&\quad \overleftrightarrow{Z}&\quad \overleftrightarrow{Z}\\ \overleftrightarrow{Z}&\quad \overleftrightarrow{Z}&\quad \overleftrightarrow{Z}&\quad \overleftrightarrow{Z}&\quad \overleftrightarrow{Z}&\quad \overleftrightarrow{Z}&\quad \overleftrightarrow{Z}\\ \overleftrightarrow{Z}&\quad \overleftrightarrow{Z}&\quad \overleftrightarrow{Z}&\quad \overleftrightarrow{Z}&\quad \overleftrightarrow{Z}&\quad \overleftrightarrow{Z}&\quad \overleftrightarrow{Z}\end{array}\right], \overrightarrow{S}=\left\{\begin{array}{c}\overrightarrow{U}\\ \overrightarrow{V}\\ \overrightarrow{W}\\ {\overrightarrow{\phi }}_{X}\\ {\overrightarrow{\phi }}_{\theta }\\ \overrightarrow{\Phi }\\ \overrightarrow{\Psi }\end{array}\right\}$$

(55)

In order to apply the boundary conditions at the boundary points of the problem, the boundary conditions are expressed as follows:

$$\overleftrightarrow{T}\overrightarrow{S}=\left\{0\right\}$$

(56)

where $\overleftrightarrow{T}$ is expressed as follows:

$$\overleftrightarrow{T}=\left[\begin{array}{cccccc}{\overleftrightarrow{T}}_{11}& {\overleftrightarrow{T}}_{12}& \cdots & \cdots & \cdots & {\overleftrightarrow{T}}_{17}\\ {\overleftrightarrow{T}}_{21}& {\overleftrightarrow{T}}_{22}& \cdots & \cdots & \cdots & {\overleftrightarrow{T}}_{27}\\ \vdots & \vdots & \vdots & \vdots & \vdots & \vdots \\ \vdots & \vdots & & & & \vdots \\ \vdots & \vdots & & & & \vdots \\ {\overleftrightarrow{T}}_{141}& {\overleftrightarrow{T}}_{142}& \cdots & \cdots & \cdots & {\overleftrightarrow{T}}_{147}\\ {\overleftrightarrow{T}}_{151}& {\overleftrightarrow{T}}_{152}& \cdots & \cdots & \cdots & {\overleftrightarrow{T}}_{157}\\ \vdots & \vdots & & & & \vdots \\ \vdots & \vdots & & & & \vdots \\ \vdots & \vdots & & & & \vdots \\ {\overleftrightarrow{T}}_{211}& {\overleftrightarrow{T}}_{212}& \cdots & \cdots & \cdots & {\overleftrightarrow{T}}_{217}\\ {\overleftrightarrow{T}}_{221}& {\overleftrightarrow{T}}_{222}& \cdots & \cdots & \cdots & {\overleftrightarrow{T}}_{227}\\ \vdots & \vdots & & & & \vdots \\ \vdots & \vdots & & & & \vdots \\ \vdots & \vdots & & & & \vdots \\ {\overleftrightarrow{T}}_{271}& {\overleftrightarrow{T}}_{272}& \cdots & \cdots & \cdots & {\overleftrightarrow{T}}_{277}\\ {\overleftrightarrow{T}}_{281}& {T}_{282}& \cdots & \cdots & \cdots & {\overleftrightarrow{T}}_{287}\end{array}\right]$$

(57)

• Boundary conditions of the clamped at the edge x = 0:

  $$ \mathop{T}\limits^{\leftrightarrow} _{11} = \left({\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}}{\mathop{I}\limits^{\theta }} \otimes \vec{I}_{1}^{x} } \right),{ }\mathop{T}\limits^{\leftrightarrow} _{12} = \mathop{T}\limits^{\leftrightarrow} _{13} = \mathop{T}\limits^{\leftrightarrow} _{14} = \mathop{T}\limits^{\leftrightarrow} _{15} = \mathop{T}\limits^{\leftrightarrow} _{16} = \mathop{T}\limits^{\leftrightarrow} _{17} = \left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}}{\mathop{Z}\limits ^{\theta }} \otimes \vec{Z}_{1}^{x} } \right) $$
  $$ \mathop{T}\limits^{\leftrightarrow} _{22} = \left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}}{\mathop{I}\limits ^{\theta }} \otimes \vec{I}_{1}^{x} } \right),\quad \mathop{T}\limits^{\leftrightarrow} _{21} = \mathop{T}\limits^{\leftrightarrow} _{23} = \mathop{T}\limits^{\leftrightarrow} _{34} = \mathop{T}\limits^{\leftrightarrow} _{25} = \mathop{T}\limits^{\leftrightarrow} _{26} = \mathop{T}\limits^{\leftrightarrow} _{27} = \left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}}{\mathop{Z}\limits ^{\theta }} \otimes \vec{Z}_{1}^{x} } \right) $$
  $$ \mathop{T}\limits^{\leftrightarrow} _{33} = \left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}}{\mathop{I}\limits ^{\theta }} \otimes \vec{I}_{1}^{x} } \right),{ }\quad \mathop{T}\limits^{\leftrightarrow} _{31} = \mathop{T}\limits^{\leftrightarrow} _{32} = \mathop{T}\limits^{\leftrightarrow} _{34} = \mathop{T}\limits^{\leftrightarrow} _{35} = \mathop{T}\limits^{\leftrightarrow} _{36} = \mathop{T}\limits^{\leftrightarrow} _{37} = \left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}}{\mathop{Z}\limits ^{\theta }} \otimes \vec{Z}_{1}^{x} } \right) $$
  $$ \mathop{T}\limits^{\leftrightarrow} _{44} = \left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}}{\mathop{I}\limits ^{\theta }} \otimes \vec{I}_{1}^{x} } \right),{ }\quad \mathop{T}\limits^{\leftrightarrow} _{41} = \mathop{T}\limits^{\leftrightarrow} _{42} = \mathop{T}\limits^{\leftrightarrow} _{43} = \mathop{T}\limits^{\leftrightarrow} _{45} = \mathop{T}\limits^{\leftrightarrow} _{46} = \mathop{T}\limits^{\leftrightarrow} _{47} = \left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}}{\mathop{Z}\limits ^{\theta }} \otimes \vec{Z}_{1}^{x} } \right) $$
  $$ \mathop{T}\limits^{\leftrightarrow} _{55} = \left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}}{\mathop{I}\limits ^{\theta }} \otimes \vec{I}_{1}^{x} } \right),{ }\quad \mathop{T}\limits^{\leftrightarrow} _{51} = \mathop{T}\limits^{\leftrightarrow} _{52} = \mathop{T}\limits^{\leftrightarrow} _{53} = \mathop{T}\limits^{\leftrightarrow} _{54} = \mathop{T}\limits^{\leftrightarrow} _{56} = \mathop{T}\limits^{\leftrightarrow} _{57} = \left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}}{\mathop{Z}\limits ^{\theta }} \otimes \vec{Z}_{1}^{x} } \right) $$
  $$ \mathop{T}\limits^{\leftrightarrow} _{66} = \left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}}{\mathop{I}\limits ^{\theta }} \otimes \vec{I}_{1}^{x} } \right),{ }\quad \mathop{T}\limits^{\leftrightarrow} _{61} = \mathop{T}\limits^{\leftrightarrow} _{62} = \mathop{T}\limits^{\leftrightarrow} _{63} = \mathop{T}\limits^{\leftrightarrow} _{64} = \mathop{T}\limits^{\leftrightarrow} _{65} = \mathop{T}\limits^{\leftrightarrow} _{67} = \left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}}{\mathop{Z}\limits^{\theta }} \otimes \vec{Z}_{1}^{x} } \right) $$
  $$ \mathop{T}\limits^{\leftrightarrow} _{77} = \left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}}{\mathop{I}\limits^{\theta }} \otimes \vec{I}_{1}^{x} } \right),\quad \mathop{T}\limits^{\leftrightarrow} _{71} = \mathop{T}\limits^{\leftrightarrow} _{72} = \mathop{T}\limits^{\leftrightarrow} _{73} = \mathop{T}\limits^{\leftrightarrow} _{74} = \mathop{T}\limits^{\leftrightarrow} _{75} = \mathop{T}\limits^{\leftrightarrow} _{76} = \left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}}{\mathop{Z}\limits ^{\theta }} \otimes \vec{Z}_{1}^{x} } \right) $$

  (58)

• Boundary conditions of the clamped at the edge θ = 0

  $$ \mathop{T}\limits^{\leftrightarrow} _{81} = \left( {\vec{I}_{1}^{\theta } \otimes {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}}{\mathop{I}\limits ^{x} }}} \right),{ }\quad \mathop{T}\limits^{\leftrightarrow} _{82} = \mathop{T}\limits^{\leftrightarrow} _{83} = \mathop{T}\limits^{\leftrightarrow} _{84} = \mathop{T}\limits^{\leftrightarrow} _{85} = \mathop{T}\limits^{\leftrightarrow} _{86} = \mathop{T}\limits^{\leftrightarrow} _{87} = \left( {\vec{Z}_{1}^{\theta } \otimes {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}}{\mathop{Z}\limits ^{x} }}} \right) $$
  $$ \mathop{T}\limits^{\leftrightarrow} _{92} = \left( {\vec{I}_{1}^{\theta } \otimes {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}}{\mathop{I}\limits^{x}}} } \right),\quad \mathop{T}\limits^{\leftrightarrow} _{91} = \mathop{T}\limits^{\leftrightarrow} _{93} = \mathop{T}\limits^{\leftrightarrow} _{94} = \mathop{T}\limits^{\leftrightarrow} _{95} = \mathop{T}\limits^{\leftrightarrow} _{96} = \mathop{T}\limits^{\leftrightarrow} _{97} = \left( {\vec{Z}_{1}^{\theta } \otimes {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}}{\mathop{Z}\limits^{x}}} } \right) $$
  $$ \mathop{T}\limits^{\leftrightarrow} _{103} = \left( {\vec{I}_{1}^{\theta } \otimes {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}}{\mathop{I}\limits ^{x} }}} \right),\quad { }\mathop{T}\limits^{\leftrightarrow} _{101} = \mathop{T}\limits^{\leftrightarrow} _{102} = \mathop{T}\limits^{\leftrightarrow} _{104} = \mathop{T}\limits^{\leftrightarrow} _{105} = \mathop{T}\limits^{\leftrightarrow} _{106} = \mathop{T}\limits^{\leftrightarrow} _{107} = \left( {\vec{Z}_{1}^{\theta } \otimes {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}}{\mathop{Z}\limits^{x}}} } \right) $$
  $$ \mathop{T}\limits^{\leftrightarrow} _{114} = \left( {\vec{I}_{1}^{\theta } \otimes {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}}{\mathop{I}\limits ^{x}}} } \right),\quad \mathop{T}\limits^{\leftrightarrow} _{111} = \mathop{T}\limits^{\leftrightarrow} _{112} = \mathop{T}\limits^{\leftrightarrow} _{113} = \mathop{T}\limits^{\leftrightarrow} _{115} = \mathop{T}\limits^{\leftrightarrow} _{116} = \mathop{T}\limits^{\leftrightarrow} _{117} = \left( {\vec{Z}_{1}^{\theta } \otimes {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}}{\mathop{Z}\limits^{x}}} } \right) $$
  $$ \mathop{T}\limits^{\leftrightarrow} _{125} = \left( {\vec{I}_{1}^{\theta } \otimes {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}}{\mathop{I}\limits ^{x}}} } \right),{ }\quad { }\mathop{T}\limits^{\leftrightarrow} _{121} = \mathop{T}\limits^{\leftrightarrow} _{122} = \mathop{T}\limits^{\leftrightarrow} _{123} = \mathop{T}\limits^{\leftrightarrow} _{124} = \mathop{T}\limits^{\leftrightarrow} _{126} = \mathop{T}\limits^{\leftrightarrow} _{127} = \left( {\vec{Z}_{1}^{\theta } \otimes {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}}{\mathop{Z}\limits ^{x} }}} \right) $$
  $$ \mathop{T}\limits^{\leftrightarrow} _{136} = \left( {\vec{I}_{1}^{\theta } \otimes {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}}{\mathop{I}\limits ^{x}}} } \right),\quad \mathop{T}\limits^{\leftrightarrow} _{131} = \mathop{T}\limits^{\leftrightarrow} _{132} = \mathop{T}\limits^{\leftrightarrow} _{133} = \mathop{T}\limits^{\leftrightarrow} _{134} = \mathop{T}\limits^{\leftrightarrow} _{135} = \mathop{T}\limits^{\leftrightarrow} _{137} = \left( {\vec{Z}_{1}^{\theta } \otimes {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}}{\mathop{Z}\limits ^{x} }}} \right) $$
  $$ \mathop{T}\limits^{\leftrightarrow} _{147} = \left( {\vec{I}_{1}^{\theta } \otimes {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}}{\mathop{I}\limits ^{x} }}} \right),{ }\quad \mathop{T}\limits^{\leftrightarrow} _{141} = \mathop{T}\limits^{\leftrightarrow} _{142} = \mathop{T}\limits^{\leftrightarrow} _{143} = \mathop{T}\limits^{\leftrightarrow} _{144} = \mathop{T}\limits^{\leftrightarrow} _{145} = \mathop{T}\limits^{\leftrightarrow} _{146} = \left( {\vec{Z}_{1}^{\theta } \otimes {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}}{\mathop{Z}\limits^{x} }}} \right) $$

  (59)

• Boundary conditions of the clamped at the edge x = L:

  $$ \mathop{T}\limits^{\leftrightarrow} _{151} = \left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}}{\mathop{I}\limits^{\theta }} \otimes \vec{I}_{Nx}^{x} } \right),\quad { }\mathop{T}\limits^{\leftrightarrow} _{152} = \mathop{T}\limits^{\leftrightarrow} _{153} = \mathop{T}\limits^{\leftrightarrow} _{154} = \mathop{T}\limits^{\leftrightarrow} _{155} = \mathop{T}\limits^{\leftrightarrow} _{156} = \mathop{T}\limits^{\leftrightarrow} _{157} = \left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}}{\mathop{Z}\limits^{\theta }} \otimes \vec{Z}_{Nx}^{x} } \right) $$
  $$ \mathop{T}\limits^{\leftrightarrow} _{162} = \left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}}{\mathop{I}\limits ^{\theta }} \otimes \vec{I}_{Nx}^{x} } \right),\quad \mathop{T}\limits^{\leftrightarrow} _{161} = \mathop{T}\limits^{\leftrightarrow} _{163} = \mathop{T}\limits^{\leftrightarrow} _{164} = \mathop{T}\limits^{\leftrightarrow} _{165} = \mathop{T}\limits^{\leftrightarrow} _{166} = \mathop{T}\limits^{\leftrightarrow} _{167} = \left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}}{\mathop{Z}\limits ^{\theta} } \otimes \vec{Z}_{Nx}^{x} } \right) $$
  $$ \mathop{T}\limits^{\leftrightarrow} _{173} = \left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}}{\mathop{I}\limits ^{\theta }} \otimes \vec{I}_{Nx}^{x} } \right),\quad \mathop{T}\limits^{\leftrightarrow} _{171} = \mathop{T}\limits^{\leftrightarrow} _{172} = \mathop{T}\limits^{\leftrightarrow} _{174} = \mathop{T}\limits^{\leftrightarrow} _{175} = \mathop{T}\limits^{\leftrightarrow} _{176} = \mathop{T}\limits^{\leftrightarrow} _{177} = \left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}}{\mathop{Z}\limits ^{\theta }} \otimes \vec{Z}_{Nx}^{x} } \right) $$
  $$ \mathop{T}\limits^{\leftrightarrow} _{184} = \left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}}{\mathop{I}\limits ^{\theta }} \otimes \vec{I}_{Nx}^{x} } \right),\quad \mathop{T}\limits^{\leftrightarrow} _{181} = \mathop{T}\limits^{\leftrightarrow} _{182} = \mathop{T}\limits^{\leftrightarrow} _{183} = \mathop{T}\limits^{\leftrightarrow} _{185} = \mathop{T}\limits^{\leftrightarrow} _{186} = \mathop{T}\limits^{\leftrightarrow} _{187} = \left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}}{\mathop{Z}\limits^{\theta }} \otimes \vec{Z}_{Nx}^{x} } \right) $$
  $$ \mathop{T}\limits^{\leftrightarrow} _{195} = \left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}}{\mathop{I}\limits^{\theta }} \otimes \vec{I}_{Nx}^{x} } \right),\quad { }\mathop{T}\limits^{\leftrightarrow} _{191} = \mathop{T}\limits^{\leftrightarrow} _{192} = \mathop{T}\limits^{\leftrightarrow} _{193} = \mathop{T}\limits^{\leftrightarrow} _{194} = \mathop{T}\limits^{\leftrightarrow} _{196} = \mathop{T}\limits^{\leftrightarrow} _{197} = \left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}}{\mathop{Z}\limits ^{\theta }} \otimes \vec{Z}_{Nx}^{x} } \right) $$
  $$ \mathop{T}\limits^{\leftrightarrow} _{206} = \left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}}{\mathop{I}\limits ^{\theta }} \otimes \vec{I}_{Nx}^{x} } \right),\quad \mathop{T}\limits^{\leftrightarrow} _{201} = \mathop{T}\limits^{\leftrightarrow} _{202} = \mathop{T}\limits^{\leftrightarrow} _{203} = \mathop{T}\limits^{\leftrightarrow} _{204} = \mathop{T}\limits^{\leftrightarrow} _{205} = \mathop{T}\limits^{\leftrightarrow} _{207} = \left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}}{\mathop{Z}\limits^{\theta }} \otimes \vec{Z}_{Nx}^{x} } \right) $$
  $$ \mathop{T}\limits^{\leftrightarrow} _{217} = \left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}}{\mathop{I}\limits ^{\theta }} \otimes \vec{I}_{Nx}^{x} } \right),\quad \mathop{T}\limits^{\leftrightarrow} _{211} = \mathop{T}\limits^{\leftrightarrow} _{212} = \mathop{T}\limits^{\leftrightarrow} _{213} = \mathop{T}\limits^{\leftrightarrow} _{214} = \mathop{T}\limits^{\leftrightarrow} _{215} = \mathop{T}\limits^{\leftrightarrow} _{216} = \left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}}{\mathop{Z}\limits ^{\theta }} \otimes \vec{Z}_{Nx}^{x} } \right) $$

  (60)

• Boundary conditions of the clamped at the edge $\theta$=${\theta }_{0}$:

  $$ \mathop{T}\limits^{\leftrightarrow} _{221} = \left( {\vec{I}_{N\theta }^{\theta } \otimes {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}}{\mathop{I}\limits ^{x}}} } \right),\quad \mathop{T}\limits^{\leftrightarrow} _{222} = \mathop{T}\limits^{\leftrightarrow} _{223} = \mathop{T}\limits^{\leftrightarrow} _{224} = \mathop{T}\limits^{\leftrightarrow} _{225} = \mathop{T}\limits^{\leftrightarrow} _{226} = \mathop{T}\limits^{\leftrightarrow} _{227} = \left( {\vec{Z}_{N\theta }^{\theta } \otimes {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}}{\mathop{Z}\limits ^{x}}} } \right) $$
  $$ \mathop{T}\limits^{\leftrightarrow} _{232} = \left( {\vec{I}_{N\theta }^{\theta } \otimes {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}}{\mathop{I}\limits ^{x}}} } \right),\quad \mathop{T}\limits^{\leftrightarrow} _{231} = \mathop{T}\limits^{\leftrightarrow} _{233} = \mathop{T}\limits^{\leftrightarrow} _{234} = \mathop{T}\limits^{\leftrightarrow} _{235} = \mathop{T}\limits^{\leftrightarrow} _{236} = \mathop{T}\limits^{\leftrightarrow} _{237} = \left( {\vec{Z}_{N\theta }^{\theta } \otimes {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}}{\mathop{Z}\limits ^{x}}} } \right) $$
  $$ \mathop{T}\limits^{\leftrightarrow} _{243} = \left( {\vec{I}_{N\theta }^{\theta } \otimes {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}}{\mathop{I}\limits ^{x}}} } \right),\quad \mathop{T}\limits^{\leftrightarrow} _{241} = \mathop{T}\limits^{\leftrightarrow} _{242} = \mathop{T}\limits^{\leftrightarrow} _{244} = \mathop{T}\limits^{\leftrightarrow} _{245} = \mathop{T}\limits^{\leftrightarrow} _{246} = \mathop{T}\limits^{\leftrightarrow} _{247} = \left( {\vec{Z}_{N\theta }^{\theta } \otimes {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}}{\mathop{Z}\limits ^{x}}} } \right) $$
  $$ \mathop{T}\limits^{\leftrightarrow} _{254} = \left( {\vec{I}_{N\theta }^{\theta } \otimes {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}}{\mathop{I}\limits ^{x}}} } \right),\quad \mathop{T}\limits^{\leftrightarrow} _{251} = \mathop{T}\limits^{\leftrightarrow} _{252} = \mathop{T}\limits^{\leftrightarrow} _{253} = \mathop{T}\limits^{\leftrightarrow} _{255} = \mathop{T}\limits^{\leftrightarrow} _{256} = \mathop{T}\limits^{\leftrightarrow} _{257} = \left( {\vec{Z}_{N\theta }^{\theta } \otimes {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}}{\mathop{Z}\limits ^{x} }}} \right) $$
  $$ \mathop{T}\limits^{\leftrightarrow} _{265} = \left( {\vec{I}_{N\theta }^{\theta } \otimes {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}}{\mathop{I}\limits ^{x}}} } \right),\quad \mathop{T}\limits^{\leftrightarrow} _{261} = \mathop{T}\limits^{\leftrightarrow} _{262} = \mathop{T}\limits^{\leftrightarrow} _{263} = \mathop{T}\limits^{\leftrightarrow} _{264} = \mathop{T}\limits^{\leftrightarrow} _{266} = \mathop{T}\limits^{\leftrightarrow} _{267} = \left( {\vec{Z}_{N\theta }^{\theta } \otimes {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}}{\mathop{Z}\limits^{x} }}} \right) $$
  $$ \mathop{T}\limits^{\leftrightarrow} _{276} = \left( {\vec{I}_{N\theta }^{\theta } \otimes {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}}{\mathop{I}\limits ^{x}}} } \right),\quad \mathop{T}\limits^{\leftrightarrow} _{271} = \mathop{T}\limits^{\leftrightarrow} _{272} = \mathop{T}\limits^{\leftrightarrow} _{273} = \mathop{T}\limits^{\leftrightarrow} _{274} = \mathop{T}\limits^{\leftrightarrow} _{275} = \mathop{T}\limits^{\leftrightarrow} _{277} = \left( {\vec{Z}_{N\theta }^{\theta } \otimes {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}}{\mathop{Z}\limits ^{x} }}} \right) $$
  $$ \mathop{T}\limits^{\leftrightarrow} _{287} = \left( {\vec{I}_{N\theta }^{\theta } \otimes {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}}{\mathop{I}\limits^{x}}} } \right),\quad \mathop{T}\limits^{\leftrightarrow} _{281} = \mathop{T}\limits^{\leftrightarrow} _{282} = \mathop{T}\limits^{\leftrightarrow} _{283} = \mathop{T}\limits^{\leftrightarrow} _{284} = \mathop{T}\limits^{\leftrightarrow} _{285} = \mathop{T}\limits^{\leftrightarrow} _{286} = \left( {\vec{Z}_{N\theta }^{\theta } \otimes {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}}{\mathop{Z}\limits^{x} }}} \right) $$

  (61)

• Simply boundary conditions at the edge x = 0:

  $$ \mathop{T}\limits^{\leftrightarrow} _{11} = A_{11} \left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}}{\mathop{I}\limits ^{\theta }} \otimes \vec{A}_{1}^{x} } \right) + A_{12} \frac{sin\alpha }{{a_{0} }}\left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}}{\mathop{I}\limits ^{\theta }} \otimes \vec{I}_{1}^{x} } \right),{ }\mathop{T}\limits^{\leftrightarrow} _{12} = \mathop{T}\limits^{\leftrightarrow} _{13} = \mathop{T}\limits^{\leftrightarrow} _{15} = \mathop{T}\limits^{\leftrightarrow} _{16} = \mathop{T}\limits^{\leftrightarrow} _{17} = \left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}}{\mathop{Z}\limits ^{\theta }} \otimes \vec{Z}_{1}^{x} } \right),{ }\mathop{T}\limits^{\leftrightarrow} _{14} = B_{11} \left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}}{\mathop{I}\limits ^{\theta }} \otimes \vec{A}_{1}^{x} } \right) + B_{12} \frac{sin\alpha }{{a_{0} }}\left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}}{\mathop{I}\limits ^{\theta }} \otimes \vec{I}_{1}^{x} } \right) $$
  $$ \mathop{T}\limits^{\leftrightarrow} _{22} = \left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}}{\mathop{I}\limits ^{\theta }} \otimes \vec{I}_{1}^{x} } \right),{ }\mathop{T}\limits^{\leftrightarrow} _{21} = \mathop{T}\limits^{\leftrightarrow} _{23} = \mathop{T}\limits^{\leftrightarrow} _{24} = \mathop{T}\limits^{\leftrightarrow} _{25} = \mathop{T}\limits^{\leftrightarrow} _{26} = \mathop{T}\limits^{\leftrightarrow} _{27} = \left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}}{\mathop{I}\limits ^{\theta }} \otimes \vec{Z}_{1}^{x} } \right) $$
  $$ \mathop{T}\limits^{\leftrightarrow} _{33} = \left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}}{\mathop{I}\limits ^{\theta }} \otimes \vec{I}_{1}^{x} } \right),\quad { }\mathop{T}\limits^{\leftrightarrow} _{31} = \mathop{T}\limits^{\leftrightarrow} _{32} = \mathop{T}\limits^{\leftrightarrow} _{34} = \mathop{T}\limits^{\leftrightarrow} _{35} = \mathop{T}\limits^{\leftrightarrow} _{36} = \mathop{T}\limits^{\leftrightarrow} _{37} = \left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}}{\mathop{I}\limits ^{\theta }} \otimes \vec{Z}_{1}^{x} } \right) $$
  $$ \mathop{T}\limits^{\leftrightarrow} _{41} = B_{11} \left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}}{\mathop{I}\limits ^{\theta }} \otimes \vec{A}_{1}^{x} } \right) + B_{12} \frac{sin\alpha }{{a_{0} }}\left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}}{\mathop{I}\limits ^{\theta }} \otimes \vec{I}_{1}^{x} } \right),{ }\quad \mathop{T}\limits^{\leftrightarrow} _{42} = \mathop{T}\limits^{\leftrightarrow} _{43} = \mathop{T}\limits^{\leftrightarrow} _{45} = \mathop{T}\limits^{\leftrightarrow} _{46} = \mathop{T}\limits^{\leftrightarrow} _{47} = \left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}}{\mathop{I}\limits ^{\theta }} \otimes \vec{Z}_{1}^{x} } \right) $$
  $$ \mathop{T}\limits^{\leftrightarrow} _{44} = D_{11} \left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}}{\mathop{I}\limits ^{\theta }} \otimes \vec{A}_{1}^{x} } \right) + D_{12} \frac{sin\alpha }{{a_{0} }}\left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}}{\mathop{I}\limits ^{\theta }} \otimes \vec{I}_{1}^{x} } \right) $$
  $$ \mathop{T}\limits^{\leftrightarrow} _{55} = \left( {I^{\theta } \otimes I_{1}^{x} } \right),\quad \mathop{T}\limits^{\leftrightarrow} _{51} = \mathop{T}\limits^{\leftrightarrow} _{52} = \mathop{T}\limits^{\leftrightarrow} _{53} = \mathop{T}\limits^{\leftrightarrow} _{54} = \mathop{T}\limits^{\leftrightarrow} _{56} = \mathop{T}\limits^{\leftrightarrow} _{57} = \left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}}{\mathop{Z}\limits^{\theta }} \otimes \vec{Z}_{1}^{x} } \right) $$
  $$ \mathop{T}\limits^{\leftrightarrow} _{66} = \left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}}{\mathop{I}\limits^{\theta }} \otimes \vec{I}_{1}^{x} } \right),{ }\mathop{T}\limits^{\leftrightarrow} _{61} = \mathop{T}\limits^{\leftrightarrow} _{62} = \mathop{T}\limits^{\leftrightarrow} _{63} = \mathop{T}\limits^{\leftrightarrow} _{64} = \mathop{T}\limits^{\leftrightarrow} _{65} = \mathop{T}\limits^{\leftrightarrow} _{67} = \left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}}{\mathop{Z}\limits ^{\theta }} \otimes \vec{Z}_{1}^{x} } \right) $$
  $$ \mathop{T}\limits^{\leftrightarrow} _{77} = \left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}}{\mathop{I}\limits ^{\theta }} \otimes \vec{I}_{1}^{x} } \right),{ }\mathop{T}\limits^{\leftrightarrow} _{71} = \mathop{T}\limits^{\leftrightarrow} _{72} = \mathop{T}\limits^{\leftrightarrow} _{73} = \mathop{T}\limits^{\leftrightarrow} _{74} = \mathop{T}\limits^{\leftrightarrow} _{75} = \mathop{T}\limits^{\leftrightarrow} _{76} = \left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}}{\mathop{Z}\limits ^{\theta }} \otimes \vec{Z}_{1}^{x} } \right) $$

  (62)

• Simply boundary conditions at the edge θ = 0:

  $$ \begin{aligned} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}} {T} _{{81}} & = \left( {\vec{I}_{1}^{\theta } \otimes \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}} {I} ^{x} } \right),\quad \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}} {T} _{{82}} = \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}} {T} _{{83}} = \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}} {T} _{{84}} = \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}} {T} _{{85}} = \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}} {T} _{{86}} = \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}} {T} _{{87}} = \left( {\vec{Z}_{1}^{\theta } \otimes \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}} {Z} ^{x} } \right) \\ \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}} {T} _{{92}} & = A_{{22}} \left( {\vec{A}_{1}^{\theta } \otimes \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}} {a} _{1} } \right),\quad \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}} {T} _{{91}} = \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}} {T} _{{93}} = \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}} {T} _{{94}} = \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}} {T} _{{96}} = \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}} {T} _{{97}} = \left( {\vec{Z}_{1}^{\theta } \otimes \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}} {Z} ^{x} } \right),\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}} {T} _{{95}} = B_{{22}} \left( {\vec{A}_{1}^{\theta } \otimes \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}} {a} _{1} } \right), \\ \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}} {T} _{{103}} & = \left( {\vec{I}_{1}^{\theta } \otimes \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}} {I} ^{x} } \right),\quad {\text{~}}\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}} {T} _{{101}} = \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}} {T} _{{102}} = \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}} {T} _{{104}} = \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}} {T} _{{105}} = \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}} {T} _{{106}} = \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}} {T} _{{107}} = \left( {\vec{Z}_{1}^{\theta } \otimes \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}} {Z} ^{x} } \right), \\ \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}} {T} _{{114}} & = \left( {\vec{I}_{1}^{\theta } \otimes \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}} {I} ^{x} } \right),\quad {\text{~}}\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}} {T} _{{112}} = \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}} {T} _{{113}} = \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}} {T} _{{114}} = \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}} {T} _{{115}} = \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}} {T} _{{116}} = \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}} {T} _{{117}} = \left( {\vec{Z}_{1}^{\theta } \otimes \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}} {Z} ^{x} } \right), \\ \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}} {T} _{{122}} & = B_{{22}} \left( {\vec{A}_{1}^{\theta } \otimes \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}} {a} _{1} } \right),\quad \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}} {T} _{{121}} = \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}} {T} _{{123}} = \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}} {T} _{{124}} = \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}} {T} _{{126}} = \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}} {T} _{{127}} = \left( {\vec{Z}_{1}^{\theta } \otimes \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}} {Z} ^{x} } \right),{\text{~}}\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}} {T} _{{125}} = D_{{22}} \left( {\vec{A}_{1}^{\theta } \otimes \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}} {a} _{1} } \right), \\ \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}} {T} _{{136}} & = \left( {\vec{I}_{1}^{\theta } \otimes \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}} {I} ^{x} } \right),\quad \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}} {T} _{{131}} = \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}} {T} _{{132}} = \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}} {T} _{{133}} = \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}} {T} _{{134}} = \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}} {T} _{{135}} = \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}} {T} _{{137}} = \left( {\vec{Z}_{1}^{\theta } \otimes \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}} {Z} ^{x} } \right), \\ \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}} {T} _{{147}} & = \left( {\vec{I}_{1}^{\theta } \otimes \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}} {I} ^{x} } \right),\quad \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}} {T} _{{141}} = \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}} {T} _{{142}} = \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}} {T} _{{143}} = \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}} {T} _{{144}} = \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}} {T} _{{145}} = \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}} {T} _{{146}} = \left( {\vec{Z}_{1}^{\theta } \otimes \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}} {Z} ^{x} } \right) \\ \end{aligned} $$

  (63)

• Simply boundary conditions at the edge x = L:

  $$ \begin{aligned} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}} {T} _{{151}} & = A_{{11}} \left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}} {I} ^{\theta } \otimes \vec{A}_{{Nx}}^{x} } \right) + A_{{12}} \frac{{sin\alpha }}{b}\left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}} {I} ^{\theta } \otimes \vec{I}_{{Nx}}^{x} } \right),~~~\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}} {T} _{{152}} = \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}} {T} _{{153}} = \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}} {T} _{{155}} = \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}} {T} _{{156}} = \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}} {T} _{{157}} = \left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}} {Z} ^{\theta } \otimes \vec{Z}_{{Nx}}^{x} } \right),~~~\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}} {T} _{{154}} = B_{{11}} \left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}} {I} ^{\theta } \otimes \vec{A}_{{Nx}}^{x} } \right) + B_{{12}} \frac{{sin\alpha }}{b}\left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}} {I} ^{\theta } \otimes \vec{I}_{{Nx}}^{x} } \right) \\ \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}} {T} _{{162}} & = \left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}} {I} ^{\theta } \otimes \vec{I}_{{Nx}}^{x} } \right),~~\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}} {T} _{{161}} = \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}} {T} _{{163}} = \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}} {T} _{{164}} = \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}} {T} _{{165}} = \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}} {T} _{{166}} = \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}} {T} _{{167}} = \left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}} {Z} ^{\theta } \otimes \vec{Z}_{{Nx}}^{x} } \right) \\ \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}} {T} _{{173}} & = \left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}} {I} ^{\theta } \otimes \vec{I}_{{Nx}}^{x} } \right),~~\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}} {T} _{{171}} = \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}} {T} _{{172}} = \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}} {T} _{{174}} = \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}} {T} _{{175}} = \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}} {T} _{{176}} = \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}} {T} _{{177}} = \left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}} {Z} ^{\theta } \otimes \vec{Z}_{{Nx}}^{x} } \right) \\ \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}} {T} _{{181}} & = B_{{11}} \left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}} {I} ^{\theta } \otimes \vec{A}_{{Nx}}^{x} } \right) + B_{{12}} \frac{{sin\alpha }}{b}\left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}} {I} ^{\theta } \otimes \vec{I}_{{Nx}}^{x} } \right),~~\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}} {T} _{{182}} = \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}} {T} _{{183}} = \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}} {T} _{{185}} = \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}} {T} _{{186}} = \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}} {T} _{{187}} = \left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}} {Z} ^{\theta } \otimes \vec{Z}_{{Nx}}^{x} } \right),~~~\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}} {T} _{{184}} = D_{{11}} \left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}} {I} ^{\theta } \otimes \vec{A}_{{Nx}}^{x} } \right) + D_{{12}} \frac{{sin\alpha }}{b}\left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}} {I} ^{\theta } \otimes \vec{I}_{{Nx}}^{x} } \right) \\ \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}} {T} _{{195}} & = \left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}} {I} ^{\theta } \otimes \vec{I}_{{Nx}}^{x} } \right),~\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}} {T} _{{191}} = \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}} {T} _{{192}} = \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}} {T} _{{193}} = \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}} {T} _{{194}} = \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}} {T} _{{196}} = \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}} {T} _{{197}} = \left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}} {Z} ^{\theta } \otimes \vec{Z}_{{Nx}}^{x} } \right) \\ \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}} {T} _{{206}} & = \left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}} {I} ^{\theta } \otimes \vec{I}_{{Nx}}^{x} } \right),~\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}} {T} _{{201}} = \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}} {T} _{{202}} = \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}} {T} _{{203}} = \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}} {T} _{{204}} = \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}} {T} _{{205}} = \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}} {T} _{{207}} = \left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}} {Z} ^{\theta } \otimes \vec{Z}_{{Nx}}^{x} } \right) \\ \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}} {T} _{{217}} & = \left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}} {I} ^{\theta } \otimes \vec{I}_{{Nx}}^{x} } \right),~~\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}} {T} _{{211}} = \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}} {T} _{{212}} = \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}} {T} _{{213}} = \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}} {T} _{{214}} = \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}} {T} _{{215}} = \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}} {T} _{{216}} = \left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}} {Z} ^{\theta } \otimes \vec{Z}_{{Nx}}^{x} } \right) \\ \end{aligned} $$

  (64)

• Simply boundary conditions at the edge $\theta$=${\theta }_{0}$:

  $$\begin{aligned} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}} {T} _{{221}} & = \left( {\vec{I}_{{N\theta }}^{\theta } \otimes \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}} {I} ^{x} } \right) \\ ~\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}} {T} _{{222}} & = \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}} {T} _{{223}} = \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}} {T} _{{224}} = \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}} {T} _{{225}} = \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}} {T} _{{226}} = \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}} {T} _{{227}} = \left( {\vec{Z}_{{N\theta }}^{\theta } \otimes \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}} {Z} ^{x} } \right) \\ \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}} {T} _{{232}} & = A_{{22}} \left( {\vec{A}_{{N\theta }}^{\theta } \otimes \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}} {a} _{1} } \right) \\ \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}} {T} _{{231}} & = \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}} {T} _{{233}} = \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}} {T} _{{234}} = \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}} {T} _{{236}} = \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}} {T} _{{237}} = \left( {\vec{Z}_{{N\theta }}^{\theta } \otimes \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}} {Z} ^{x} } \right) \\ \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}} {T} _{{235}} & = B_{{22}} \left( {\vec{A}_{{N\theta }}^{\theta } \otimes \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}} {a} _{1} } \right) \\ \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}} {T} _{{243}} & = \left( {\vec{I}_{{N\theta }}^{\theta } \otimes \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}} {I} ^{x} } \right) \\ \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}} {T} _{{241}} & = \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}} {T} _{{242}} = \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}} {T} _{{244}} = \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}} {T} _{{245}} = \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}} {T} _{{246}} = \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}} {T} _{{247}} = \left( {\vec{Z}_{{N\theta }}^{\theta } \otimes \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}} {Z} ^{x} } \right) \\ \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}} {T} _{{254}} & = \left( {\vec{I}_{{N\theta }}^{\theta } \otimes \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}} {I} ^{x} } \right) \\ \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}} {T} _{{252}} & = \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}} {T} _{{253}} = \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}} {T} _{{254}} = \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}} {T} _{{255}} = \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}} {T} _{{256}} = \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}} {T} _{{257}} = \left( {\vec{Z}_{{N\theta }}^{\theta } \otimes \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}} {Z} ^{x} } \right) \\ \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}} {T} _{{262}} & = B_{{22}} \left( {\vec{A}_{{N\theta }}^{\theta } \otimes \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}} {a} _{1} } \right) \\ \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}} {T} _{{261}} & = \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}} {T} _{{263}} = \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}} {T} _{{264}} = \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}} {T} _{{266}} = \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}} {T} _{{267}} = \left( {\vec{Z}_{{N\theta }}^{\theta } \otimes \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}} {Z} ^{x} } \right) \\ \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}} {T} _{{262}} & = B_{{22}} \left( {\vec{A}_{{N\theta }}^{\theta } \otimes \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}} {a} _{1} } \right) \\ \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}} {T} _{{261}} & = \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}} {T} _{{263}} = \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}} {T} _{{264}} = \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}} {T} _{{266}} = \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}} {T} _{{267}} = \left( {\vec{Z}_{{N\theta }}^{\theta } \otimes \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}} {Z} ^{x} } \right) \\ \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}} {T} _{{276}} & = \left( {\vec{I}_{{N\theta }}^{\theta } \otimes \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}} {I} ^{x} } \right) \\ \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}} {T} _{{271}} & = \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}} {T} _{{272}} = \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}} {T} _{{273}} = \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}} {T} _{{274}} = \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}} {T} _{{275}} = \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}} {T} _{{277}} = \left( {\vec{Z}_{{N\theta }}^{\theta } \otimes \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}} {Z} ^{x} } \right) \\ \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}} {T} _{{287}} & = \left( {\vec{I}_{{N\theta }}^{\theta } \otimes \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}} {I} ^{x} } \right) \\ \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}} {T} _{{281}} & = \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}} {T} _{{282}} = \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}} {T} _{{283}} = \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}} {T} _{{284}} = \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}} {T} _{{285}} = \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}} {T} _{{286}} = \left( {\vec{Z}_{{N\theta }}^{\theta } \otimes \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}} {Z} ^{x} } \right) \\ \end{aligned} $$

  (65)

By removing the governing equation at the boundary points, Eq. (54) can be expressed as follows:

$$ \overleftrightarrow {\overline{K}} \vec{S} = \omega^{2} \overleftrightarrow {\overline{M}} \vec{S} $$

(66)

By separating the columns corresponding to the border and middle points in Eqs. (54) and (58), these relationships can be expressed as follows:

$$ \overleftrightarrow {\overline{K}}_{b} \vec{S}_{b} + \overleftrightarrow {\overline{K}}_{d} \vec{S}_{d} = \omega^{2} \left( {\overleftrightarrow {\overline{M}}_{b} \vec{S}_{b} + \overleftrightarrow {\overline{M}}_{d} \vec{S}_{d} } \right) $$

(67a)

$$ \mathop{T}\limits^{\leftrightarrow} {}_{b} \vec{S}_{b} + \mathop{T}\limits^{\leftrightarrow} _{d} \vec{S}_{d} = \left\{ 0 \right\} $$

(67b)

Using Eq. (67b), the following relation can be expressed between the displacement at the boundary and intermediate points:

$$ \vec{S}_{b} = \mathop{P}\limits^{\leftrightarrow} \vec{S}_{d} $$

(68)

in which

$$ \mathop{P}\limits^{\leftrightarrow} = - \mathop{T}\limits^{\leftrightarrow} {}_{b}^{ - 1} T_{d} $$

(69)

By inserting Eq. (68) into Eq. (67a), the following relation can be expressed:

$$ \mathop{K}\limits^{\leftrightarrow} {}^{*} \vec{S}_{d} = \omega^{2} \mathop{M}\limits^{\leftrightarrow} {}^{*} \vec{S}_{d} $$

(70)

in which

$$ \mathop{K}\limits^{\leftrightarrow} {}^{*} = \overleftrightarrow {\overline{K}}_{d} + \overleftrightarrow {\overline{K}}_{b} \mathop{P}\limits^{\leftrightarrow} $$

(71)

$$ \mathop{M}\limits^{\leftrightarrow} {}^{*} = \overleftrightarrow {\overline{M}}_{d} + \overleftrightarrow {\overline{M}}_{b} \mathop{P}\limits^{\leftrightarrow} $$

(72)

The above equation is an eigenvalue problem and its solution process is as follows:

• First, the nonlinear term in (71) is omitted, and as a result, the linear eigenvalue and its corresponding eigenvector are obtained.

• Using the linear eigenvalue, the nonlinear term can be evaluated. By inserting the nonlinear expression in the eigenvalue problem, the nonlinear eigenvalue and the corresponding eigenvector will be obtained.

• The above process continues until the eigenvalues ​​for two consecutive values satisfy the following convergence relation.

$$ \frac{{||\omega_{NL} |^{r + 1} - |\omega_{NL} |^{r} |}}{{|\omega_{NL} |^{r} }} < 0.01 $$

(73)