1 Introduction

Considerable progress has been made in the past few decades in understanding the electrotechnical effects of dielectric materials due to their applications in energy storage capacitors [1], electric power conditioning, signal processing, motor starting and tunable microwave devices [2]. One of the properties which characterize such materials is flexoelectricity.Footnote 1 This is a size-dependent effect and occurs at the nanoscale in dielectric crystals where mechanical loads from strain gradients induce spontaneous polarization. The converse flexoelectric effect corresponds to the application of an external electric field to produce elastic deformation. The flexoelectric effect was noticed in 1964 by Kogan [3], given its name in 1981 by Indenbom et al. [4], and was mathematically formulated for liquid crystals in 1969 by Meyer [5].

El-Dhaba [6,7,8,9] proposed a mathematical model with applications to study the flexoelectric effect by considering the inner structure of the material belonging to cubic symmetry, thus avoiding confusion with piezoelectricity. In a later work, Atef and El-Dhaba [10] formulated piezoelectricity and flexoelectricity with different measures at the nanoscale within the so-called reduced micromorphic model [11].

Theoretical investigations of flexoelectricity have included the development of analytical models [12,13,14,15,16] to describe the behavior of dielectrics under inhomogeneous deformation, as well as numerical simulations [15, 17] to study the effects of flexoelectricity on various physical phenomena. These studies have helped elucidate the underlying mechanisms that give rise to flexoelectricity and its associated applications.

Based on the proposed theories of flexoelectricity, wave propagation problems in dielectrics are recently attracting more attention. Mirzade [18] studied the influence of flexoelectric effect on the amplitude and velocity of nonlinear strain waves in solids. Hu et al. [19] investigated the longitudinal wave propagation in a semi-infinite elastic dielectric medium, while considering the flexoelectric effect and the micro-inertia term within the context of the strain gradient theory of elasticity. They concluded that neglecting the micro-inertia term in the strain gradient theory of elasticity leads to unbounded and physically unacceptable wave velocity and group velocity. Jiao et al. in [20] studied the dispersion of plane waves propagating for an infinite piezoelectric material and the reflection of waves at the free surface. They found that the dispersion characteristics of the coupled elastic waves are fundamentally influenced by the micro-inertial effect. In addition, Jiao et al. [21] examined how plane waves behaved when passing through a flexoelectric, piezoelectric slab that was encased in two piezoelectric half-spaces, they discovered that the flexoelectric coefficients and two characteristic lengths of the microstructure had an impact on how waves propagated. They concluded that the \(P\)-type and the \(S\)-type surface waves are two new wave propagation modes that are caused by microstructure effects, and that both the micro-inertial and the strain gradient effects have an impact on both reflection and transmission waves. This can be explained by the fact that the inertial effect increases the material's effective inertance, while the strain gradient effect increases the material's effective elasticity.

The dispersion characteristics of the coupled elastic waves are fundamentally influenced by the micro-inertial effect. In their study of plane wave propagation in a micro-structured flexoelectric solid half-space, Singh and Gupta [22] demonstrated the existence of certain types of plane waves. They concluded that at very high wave numbers, the influence of the strain gradient causes the phase speeds to become unbounded and the plane waves to disperse. Additionally, plane waves propagate much more quickly in media with the strain gradient effect alone, and much slower in a medium with the flexoelectric effect alone. In a medium having a micro-inertia effect alone, the plane waves are also seen to propagate slower.

Analysis of the flexoelectric effect’s impact on the propagation of Love waves in layered composite structures that have a piezoelectric layer atop a semi-infinite isotropic elastic media was investigated by Yang et al. [23]. They concluded that the propagation of Love waves is significantly impacted by the flexoelectric effect. A complicated phase velocity with a negative/positive imaginary part results from the existence of flexoelectricity, which causes Love waves either to weaken or to intensify over time. Additionally, the thickness and flexoelectric coefficients of the guiding layer have a significant impact on the phase velocity dispersion relations. It was shown that the flexoelectric effect should not be disregarded while examining the dispersion relations of surface acoustic waves propagating in nanoscale piezoelectric materials.

Yang et al. [24] studied the effects of flexoelectricity and strain gradient elasticity on Lamb waves propagating in an infinite piezoelectric nanoplate. They concluded that flexoelectricity could decrease the phase velocity, while strain gradient elasticity could increase it. Also, the effects of flexoelectricity and strain gradient elasticity largely depend on the wave number, material properties and nanoplate thickness. In addition, acoustic wave propagation problems are complicated at the nanoscale.

In his study of Rayleigh wave propagation in semi-infinite flexoelectric dielectrics with the effects of dynamic bulk flexoelectricity, strain gradient elasticity, and micro-inertia effect, Qi [25] concluded that the presence of the strain gradient elasticity and the micro-inertia term influenced the wave velocity. The dispersion curve also requires the existence of two internal length scales. These effects are effective only for larger wave numbers. Additionally, it was discovered that the static bulk flexoelectric effect lowers Rayleigh wave velocity, particularly when the static bulk flexo-coupling coefficient is large. Another study by Papargyri-Beskou, et al. [26] for wave propagation in gradient elastic solids with structures concluded that micro-inertia term is essential for realistic dispersion waves. Gupta and Singh [27] studied the influence of static and dynamic flexoelectricity, micro-inertia, and strain gradient elasticity in the longitudinal or transverse wave propagation in an elastic solid.

Special attention was paid in this work to study the dynamical flexoelectric effect due to anti-plane point load for a half-space made of isotropic, homogeneous dielectrics, which is called Flamant–Boussinesq problem. Historical data about both scientists may be found in Maugin’s work [28]. Furthermore, "Mindlin problem" is a generalisation of "Boussinesq problem" where the stresses in an elastic half-space are subject to a sub-surface point load. Clearly "Mindlin problem" [29, 30] is more realistic than the "Boussinesq problem" in determining the mechanical and physical properties of soil and rock for the design of earthworks, foundations retaining structures, oil platforms, wind turbines structures, artificial islands, and subsea pipelines [31].

A recent study by Georgiadis and Anagnostou [32] analyzed the response of isotropic elastic materials in the frame of the first strain gradient theory of elasticity subjected to concentrated loads. They proposed solutions for the Flamant–Boussinesq problem in a half-space, and Kelvin problem in a full-space under concentrated line forces. Their solution is exact and based on integral transformation. They showed that their solution is continuous and bounded at the points of application of loads, such behavior is seen to be more natural than the singular behavior of solution obtained from the classical theory of elasticity.

The present work is organized as follows: In Sect. 2, we quote the mathematical modeling of the dynamical flexoelectricity with micro-inertia effect. The mathematical formulation of Flamant–Boussinesq problem is presented in Sect. 3 with reference to previous work. The analytical wave solution is derived in Sect. 4. Numerical results, graphs, and discussion are introduced in Sect. 5. Concluding remarks are given in Sect. 6.

2 Problem formulation

Let us consider a surface \(S\)-enclosed unbounded region that is made of an elastic and an isotropic dielectric material of volume \(V\). To define the position vector of a general point on the surface with regard to a fixed point \(O\) in space, the Cartesian coordinate system \(X_{i} , i = 1, 2\), is introduced to describe the position of each point of the elastic body in the reference frame, also, \({\mathbf{R}} = X_{i} {\mathbf{E}}_{i}\), \(i = 1,2,\) 3, is the position vector defined at each point, where the unit vectors \({\mathbf{E}}_{i}\) is the basis vector for reference coordinates defined at each point in the elastic body. After deformation of the elastic body, we use the coordinates system \(x_{i} , i = 1, 2,3\), to describe the new position of each material point consisting of the elastic body, \({\mathbf{r}} = x_{i} {\mathbf{e}}_{i}\), \(i = 1,2, 3\), is the position vector for each material point after deformation, \({\mathbf{e}}_{i }\) denotes the unit base vector defined at each material point for the current coordinate system. Due to the infinitesimal deformation, the reference coordinate system and the current coordinate system coincide. For the study of the strain gradient theory of elasticity with electric interaction, the kinematic field relations, higher-gradient field relations and electric potential are defined at any point of the medium as:

$$ \varepsilon_{ij} = \frac{1}{2}\left( {u_{i,j} + u_{j,i} } \right),\quad \eta_{ijk} = \partial_{i} \varepsilon_{jk} = \frac{1}{2}\left( {u_{j,ki} + u_{k.ji} } \right),\quad E_{i} = \phi_{,i} $$
(1)

Referring to [33, 34] for details, the variation for the Hamilton functional ultimately leads to the following field equations which should be satisfied at each material point inside the surface \(S\):

$$ \left( {\sigma_{ij} - \tau_{kij,k} } \right)_{,j} + f_{i}^{ex} = \rho \ddot{u}_{i} + m_{ij} \ddot{P}_{j} - \frac{1}{3}\rho h^{2} \ddot{u}_{i,jj} , \forall r \in V , $$
(2)
$$ E_{i}^{in} - E_{i}^{ex} + \phi_{,i} = - \zeta_{ij} \ddot{P}_{j} - m_{ij} \ddot{u}_{j} , \forall r \in V, $$
(3)
$$ P_{{i,i}} - \epsilon _{0} \phi _{{,ii}} = 0,\forall ,\,{\textbf{r}} \in V, $$
(4)

the first equation represents the augmented dynamical equation of motion with dynamical displacement, dynamical polarization and micro-inertia effects, the second equation is the dynamical equation of intramolecular force balance [35] which was derived from fundamental considerations of the equilibrium of electrical forces, while the third equation is equivalent to the vanishing of the electric displacement gradient \( D_{i,i} = 0\) (equation of quasi-electrostatics without the free charge.

The boundary conditions are:

$$ \sigma_{k}^{ex} = \left( {\sigma_{jk} - \left( {\tau_{ijk,i} + \tau_{jik,i} } \right) + \frac{1}{3}\rho h^{2} \ddot{u}_{k,j} } \right)n_{j} + \tau_{ijk,l} n_{i} n_{j} n_{l} , $$
(5)
$$ \tau_{k}^{ex} = \tau_{ijk} n_{i} n_{j} , $$
(6)
$$ q^{ex} = \left( {P_{i} - \varepsilon_{0} \phi_{,i} } \right)n_{i} , $$
(7)

where \(\lambda\) and \(\mu\) are Lamé coefficients, \( \rho\)- the mass density, \(\sigma_{ij}\)- the Cauchy stress tensor components, \(u_{i}\)- the components of displacement, \(\varepsilon_{ij}\)- the strain tensor components, \( \xi_{ij}\)- the phenomenological tensor components controlling the dynamics of polarization, \(m_{ij}\)- the dynamic flexocoupling tensor components, \( \eta_{ijk}\)- the first derivatives of the strain tensor, \( \tau_{ijk}\)- the couple stress tensor components, \( D_{i}\)- the components of electric displacement, \(E_{i}\)- the components of electric field, \(P_{i}\)- the components of polarization, \(f_{i}^{ex}\)- the components of the external body force, \( \varepsilon_{0}\)- the permittivity of vacuum, \(\phi\)- the electric potential, \(h\)- the internal length scale parameter corresponding to the micro-inertia effect, \(E_{i}^{ex}\)- the external electric field components, \( E_{i}^{in}\)- the effective local electric field components, \(q^{ex}\)- the surface electric charge density, \( \sigma_{i}^{ex}\)- the components the physical traction vector, \(\tau_{i}^{ex}\)- the double traction vector components. We note that the first boundary condition for stress involves a second time derivative of the displacement gradient. Such type of boundary conditions is said to be dissipative and is due to induce damping effects.

Following [36, 37] the constitutive relations are written in the following form:

$${\sigma }_{ij}=\lambda {\delta }_{ij}{u}_{k,k}+\mu \left({u}_{i,j}+{u}_{j,i}\right),$$
(8)
$${\tau }_{ijk}=2{\alpha }_{1}{\delta }_{jk}{u}_{i,aa}+2{\alpha }_{3}\left({\delta }_{ik}{u}_{j,aa}+{\delta }_{ij}{u}_{k,aa}\right)+2\left({\alpha }_{1}+{\alpha }_{2}\right){\delta }_{jk}{u}_{a,ai}+2\left({\alpha }_{1}+{\alpha }_{3}\right)\left({\delta }_{ij}{u}_{a,ak}+{\delta }_{ik}{u}_{a,aj}\right)+2\left({\alpha }_{4}+{\alpha }_{5}\right)\left({u}_{j,ki}+{u}_{k.ij}\right)+4{\alpha }_{5}{u}_{i,jk}+{M}^{E}{\delta }_{jk}{P}_{i}+\frac{1}{2}{N}^{E}\left({\delta }_{ij}{P}_{k}+{\delta }_{ik}{P}_{j}\right),$$
(9)
$$ E_{i}^{{}} = \chi^{E} P_{i} + \left( {M^{E} + \frac{1}{2}N^{E} } \right)u_{j,ij} + \frac{1}{2}N^{E} u_{i,jj} , $$
(10)

with

$$ \chi^{E} = \frac{1}{{\varepsilon_{0} \chi }}, M^{E} = \frac{1}{{\varepsilon_{0} \chi }}\left( {\frac{{\tilde{\mu }_{1} }}{15} + \frac{{\tilde{\mu }_{2} }}{3}} \right), N^{E} = \frac{1}{{\varepsilon_{0} \chi }}\left( {\frac{2}{15}\tilde{\mu }_{1} - \frac{{\tilde{\mu }_{2} }}{3}} \right), $$
(11)

where \(\alpha_{i} , i = 1,2, \ldots ,5\) are material constants for strain gradient theory of elasticity, \(\chi\) is the electric susceptibility, \(\tilde{\mu }_{1}\) and \(\tilde{\mu }_{2}\) are the longitudinal and transverse components of the flexoelectric tensor for isotropic material, respectively, \(\frac{\partial }{{\partial x_{i} \partial x_{j} }}\left( {\boxed{}} \right) = \left( {\boxed{}} \right)_{,ij}\) is the differentiation operator and \(\delta_{jk}\) is the Krönecker delta symbol.

3 Flamant–Boussinesq problem

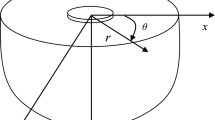
Flamant–Boussinesq problem [32, 38,39,40,41] is a two-dimensional configuration for a half-space subjected to concentrated loads in the form of line forces. Following Horgan and Miller [42], the anti-plane shear effect is always possible for any isotropic dielectric, while the anti-plane normal stress effect is generally present for an isotropic dielectrics. Consequently, in this work, we restrict further considerations to the case of an isotropic material, and the applied forces are normal wave forces at the surface of the half-space. A graphical description for the problem is shown in the following figure:

The solution is presented for the displacement, polarization, and electric potential in the half-space \(x\ge 0\), \(-\infty \le y\le \infty \) with surface at \(z=0\) made of an isotropic material, due to an applied normal wave load. All the considered functions are taken to depend only on the spatial coordinates \( x\), \(y\), in addition to time \( t\).

The solution may be taken in the following form:

$$ {\varvec{u}} = (0,0,u_{z}) ,\quad {\mathbf{P}} = (0,0,P_{z}) ,\quad {\mathbf{E}}^{in} = (0,0,E_{z} ), \quad{\mathbf{E}}^{in} = - \nabla \phi = \left(- \frac{\partial \phi }{{\partial x}},\frac{\partial \phi }{{\partial y}},0 \right), $$

with

$$ u_{z} = u_{z} \left( {x,y,t} \right), P_{z} = P_{z} \left( {x,y,t} \right), E_{z} = E_{z} \left( {x,y,t} \right), \phi = \phi \left( {x,y,t} \right). $$

The non-vanishing components of the strain tensor and its first derivatives are

$$ \begin{gathered} \varepsilon_{xz} = \frac{1}{2}\frac{{\partial u_{z} }}{\partial x},\;\varepsilon_{yz} = \frac{1}{2}\frac{{\partial u_{z} }}{\partial y},\eta_{xxz} = \frac{1}{2}\frac{{\partial^{2} u_{z} }}{{\partial x^{2} }}, \hfill \\ \eta_{yyz} = \frac{1}{2}\frac{{\partial^{2} u_{z} }}{{\partial y^{2} }},\;\eta_{yxz} = \frac{1}{2}\frac{{\partial^{2} u_{z} }}{\partial x\partial y},\;\eta_{xyz} = \frac{1}{2}\frac{{\partial^{2} u_{z} }}{\partial x\partial y}. \hfill \\ \end{gathered} $$
(12)

Therefore, Eqs. (2–4) are written as:

$$ \mu \nabla^{2} u_{z} - A\nabla^{4} u_{z} - \frac{1}{2}N^{E} \nabla^{2} P_{z} = \rho \frac{{\partial^{2} u_{z} }}{{\partial t^{2} }} + \tilde{m}\frac{{\partial^{2} P_{z} }}{{\partial t^{2} }} - \frac{1}{3}\rho h^{2} \nabla^{2} \frac{{\partial^{2} u_{z} }}{{\partial t^{2} }}, $$
(13)
$$ \chi^{E} P_{z} + \frac{1}{2}N^{E} \nabla^{2} u_{z} = - \tilde{\zeta }\frac{{\partial^{2} P_{z} }}{{\partial t^{2} }} - \tilde{m}\frac{{\partial^{2} u_{z} }}{{\partial t^{2} }}, $$
(14)
$$ \nabla^{2} \phi = 0. $$
(15)

For the dimension analysis, we use the following definitions for new dimensionless variables:

$$ \begin{array}{*{20}c} {t_{0} = \sqrt {\frac{{\rho \ell_{0}^{2} }}{\mu }} ,} & {t^{*} = \frac{t}{{t_{0} }},} & {\begin{array}{*{20}c} {\frac{{\partial^{2} }}{{\partial t^{2} }} = \frac{1}{{t_{0}^{2} }}\frac{{\partial^{2} }}{{\partial t^{*2} }},} & {x^{*} = \frac{x}{{\ell_{0} }},} & {y^{*} = \frac{y}{{\ell_{0} }},} & {\nabla^{2} = \frac{1}{{\ell_{0}^{2} }}\nabla^{*2} } \\ \end{array} } \\ \end{array} , $$

where \(t_{0}\) and \(\ell_{0}\) are the characteristic time and characteristic length, respectively. Therefore, the dimensionless physical variables are written as:

$$ u_{z}^{*} = \frac{{u_{z} }}{{\ell_{0} }}, P_{z}^{*} = \chi^{E} b_{0} P_{z} , \phi^{*} = \frac{{b_{0} }}{{\ell_{0} }}\phi , E_{z}^{*} = b_{0} E_{z}^{in} , \sigma_{ij}^{*} = \frac{{\sigma_{ij} }}{\mu }, \tau_{ijk}^{*} = \frac{{\tau_{ijk} }}{{\mu \ell_{0} }}, $$
$$ \sigma_{ij}^{{Phys^{*} }} = \frac{{\sigma_{ij}^{Phys} }}{\mu }, \sigma_{x}^{{ex^{*} }} = \frac{{\sigma_{x}^{ex} }}{\mu }, \tau_{x}^{ex} = \frac{{\tau_{x}^{ex} }}{{\mu \ell_{0} }}, q^{{ex^{*} }} = \frac{{b_{0} }}{{\varepsilon_{0} }}q^{ex} , b_{0} = \frac{{\ell_{0} }}{\mu }\frac{{\tilde{m}}}{{\tilde{\zeta }}}. $$

The asterisk will be omitted for convenience. Upon neglecting the body forces and the external electric field, Eqs. (9–11) reduce to:

$$ \nabla^{2} u_{z} - l_{1} \nabla^{4} u_{z} - l_{2} \nabla^{2} P_{z} = \frac{{\partial^{2} u_{z} }}{{\partial t^{2} }} + l_{4} \frac{{\partial^{2} P_{z} }}{{\partial t^{2} }} - l_{3} \frac{{\partial^{2} }}{{\partial t^{2} }}\left( {\nabla^{2} u_{z} } \right) $$
(16)
$$ P_{z} + l_{5} \nabla^{2} u_{z} = - l_{4} \frac{{\partial^{2} P_{z} }}{{\partial t^{2} }} - l_{6} \frac{{\partial^{2} u_{z} }}{{\partial t^{2} }}, $$
(17)
$$ \nabla^{2} \phi = 0, $$
(18)

With

$$ \begin{array}{*{20}c} {l_{1} = \frac{{At_{0}^{2} }}{{\rho \ell_{0}^{4} }},} & {l_{2} = \frac{1}{2}\frac{1}{{\ell_{0}^{2} }}\frac{{\tilde{\zeta }}}{{\tilde{m}}}\left( {\frac{2}{15}\tilde{\mu }_{1} - \frac{{\tilde{\mu }_{2} }}{3}} \right),} & {l_{3} = \frac{{h^{2} }}{{3\ell_{0}^{2} }},} \\ {l_{4} = \frac{{\varepsilon_{0} \chi }}{{t_{0}^{2} }}\tilde{\zeta },} & {l_{5} = \frac{1}{2}\frac{{\tilde{m}}}{\mu \mathop \zeta \limits }\frac{1}{{\varepsilon_{0} \chi }}\left( {\frac{2}{15}\tilde{\mu }_{1} - \frac{{\tilde{\mu }_{2} }}{3}} \right),} & {l_{6} = \frac{{\tilde{m}^{2} }}{{\rho \tilde{\zeta }}},} \\ \end{array} $$
(19)

and \(A = 2\alpha_{3} + 2\alpha_{4} + 2\alpha_{5}\), where \(\alpha_{3}\), \(\alpha_{4}\) and \(\alpha_{5}\) are strain gradient material parameters.

Equations (9–11) for the non-vanishing constitutive relations reduce to:

$$ \sigma_{xz} = \frac{{\partial u_{z} }}{\partial x}, $$
(20)
$$ \sigma_{yz} = \frac{{\partial u_{z} }}{\partial y}, $$
(21)
$$ \tau_{xzx} = l_{1} \frac{{\partial^{2} u_{z} }}{{\partial x^{2} }} + l_{7} \frac{{\partial^{2} u_{z} }}{{\partial y^{2} }} + l_{2} P_{z} , $$
(22)
$$ \tau_{yzy} = l_{1} \frac{{\partial^{2} u_{z} }}{{\partial y^{2} }} + l_{7} \frac{{\partial^{2} u_{z} }}{{\partial x^{2} }} + l_{2} P_{z} , $$
(23)
$$ \tau_{xzy} = \tau_{yzx} = l_{8} \frac{{\partial^{2} u_{z} }}{\partial x\partial y}, $$
(24)
$$ E_{z} = P_{z} + l_{5} \nabla^{2} u_{z} . $$
(25)

With

$$ l_{7} = \frac{{2\alpha_{3} }}{{\mu \ell_{0}^{2} }}, l_{8} = 2\frac{{\alpha_{4} + \alpha_{5} }}{{\mu \ell_{0}^{2} }} $$

The classical traction vector acting at the surface of the half-space, the higher-order traction forces prescribed at the surface and the external surface charges are written as:

$$ \sigma_{z}^{ex} = - \sigma_{xz} + \frac{{\partial \tau_{xzx} }}{\partial x} + \frac{{\partial \tau_{yzx} }}{\partial y} + \frac{{\partial \tau_{xzy} }}{\partial y} - l_{3} \frac{\partial }{\partial x}\left( {\frac{{\partial^{2} u_{z} }}{{\partial t^{2} }}} \right), $$
(26)
$$ \tau_{z}^{ex} = \tau_{xzx} , $$
(27)
$$ q^{ex} = \frac{\partial \phi }{{\partial x}}. $$
(28)

We note that only the \(z\)-component of the classical traction vector exists due to the shear stress, gradient of higher-order stress and micro-inertia effect. The component of the higher-order tensor \(\tau_{xzx}\) is responsible for anti-plane traction force. Moreover, the third equation gives the normal component of the electric field in terms of the electric potential, related to the surface electric charges. Equations (5–7) for the boundary conditions of Flamant–Boussinesq problem take the form:

$$ \sigma_{z}^{ex} \left( {x,y,t} \right) = f\left( {0,0,t} \right), $$
(29)
$$ \tau_{z}^{ex} = 0, $$
(30)
$$ q^{ex} = 0, $$
(31)

Or

$$ - \frac{{\partial u_{z} }}{\partial x} + l_{1} \frac{{\partial^{3} u_{z} }}{{\partial x^{3} }} + \left( {l_{7} + 2l_{8} } \right)\frac{{\partial^{3} u_{z} }}{{\partial x\partial y^{2} }} + l_{2} \frac{{\partial P_{z} }}{\partial x} - l_{3} \frac{\partial }{\partial x}\left( {\frac{{\partial^{2} u_{z} }}{{\partial t^{2} }}} \right) = f\left( {0,0,t} \right), $$
(32)
$$ l_{1} \frac{{\partial^{2} u_{z} }}{{\partial x^{2} }} + l_{7} \frac{{\partial^{2} u_{z} }}{{\partial y^{2} }} + l_{2} P_{z} = 0, $$
(33)
$$ \frac{\partial \phi }{{\partial x}} = 0. $$
(34)

Additional natural boundary conditions:

$$ u_{z} \left( {x,y,0} \right) = \left. {\frac{{\partial u_{z} \left( {x,y,t} \right)}}{\partial t}} \right|_{t = 0} = P_{z} \left( {x,y,0} \right) = \left. {\frac{{\partial P_{z} \left( {x,y,t} \right)}}{\partial t}} \right|_{t = 0} = 0. $$
(35)

Following [43, 44], the strain gradient material parameters \(\alpha_{i} , i = 1, \ldots ,5\) are given as:

$$ \left\{ {\alpha_{1} ,\alpha_{2} ,\alpha_{3} ,\alpha_{4} ,\alpha_{5} } \right\} = \frac{1}{30}\left\{ {\frac{11}{2},13, - \frac{23}{4},20, - \frac{5}{2}} \right\}\mu \ell_{0}^{2} . $$
(36)

in terms of Lamé coefficient \(\mu\) and the characteristic length \(l_{0}\).

4 Wave solution

The analytical solution of the basic equations of the problem under consideration is looked for as a harmonic wave:

$$ \left\{ {u_{z} ,P_{z} ,\phi } \right\}\left( {x,y,t} \right) = \left[ {\overline{u}_{z} ,\overline{P}_{z} ,\overline{\phi }} \right]\left( x \right){\text{e}}^{{i\left( {\ell_{0} \xi y - t_{0} \omega t} \right)}} , $$
(37)

where \(\overline{u}_{z} \left( x \right),\overline{P}_{x} \left( x \right)\) and \(\overline{\phi }\left( x \right)\) are the amplitudes of the physical quantities,\( \xi\) is the wave number, \(\omega\) is the wave frequency, and \(i\) denotes the pure imaginary unit.

Substitution from Eq. (33) into Eqs. (12–14) yields

$$ \left( {\frac{{d^{4} }}{{dx^{4} }} - a_{1} \frac{{d^{2} }}{{dx^{2} }} - a_{2} } \right)\overline{u}_{z} + \left( {a_{3} \frac{{d^{2} }}{{dx^{2} }} - a_{4} } \right)\overline{P}_{z} = 0 $$
(38)
$$ \left( {l_{5} \frac{{d^{2} }}{{dx^{2} }} - a_{5} } \right)\overline{u}_{z} + a_{6} \overline{P}_{z} = 0, $$
(39)
$$ \left( {\frac{{d^{2} }}{{dx^{2} }} - \ell_{0}^{2} \xi^{2} } \right)\overline{\phi } = 0, $$
(40)

with the following abbreviations:

$$\begin{array}{cc}{a}_{1}=\frac{1}{{l}_{1}}\left(1-{{t}}_{0}^{2}{\omega }^{2}{l}_{3}+2{\ell}_{0}^{2}{\xi }^{2}{l}_{1}\right), & {a}_{2}=\frac{1}{{l}_{1}}\left(\left(1+{\ell}_{0}^{2}{\xi }^{2}{l}_{3}\right){{t}}_{0}^{2}{\omega }^{2}-\left(1+{\ell}_{0}^{2}{\xi }^{2}{l}_{1}\right){\ell}_{0}^{2}{\xi }^{2}\right),\\ {a}_{3}=\frac{{l}_{2}}{{l}_{1}},& {a}_{4}=\frac{1}{{l}_{1}}\left({\ell}_{0}^{2}{\xi }^{2}{l}_{2}+{{t}}_{0}^{2}{\omega }^{2}{l}_{4}\right),\\ {a}_{5}={\ell}_{0}^{2}{\xi }^{2}{l}_{5}+{{t}}_{0}^{2}{\omega }^{2}{l}_{6},& {a}_{6}=1-{{t}}_{0}^{2}{\omega }^{2}{l}_{4}.\end{array}$$

Here, one takes the exponential form for the function in the boundary conditions as:

$$ f\left( {y,t} \right) = f_{0} {\text{e}}^{{i\left( {\ell_{0} \xi y - t_{0} \omega t} \right)}} , $$

where \(f_{0}\) is the amplitude of the applied wave.

Equation (36) provides the bounded solution for the electric potential function \(\phi \) in the form:

$$ \phi \left( {x,y,t} \right) = R_{0} {\text{e}}^{{i\left( {\ell_{0} \xi y - t_{0} \omega t} \right) - \ell_{0} \xi x}} , $$
(41)

where \(R_{0}\) a constant.

The coupled system of Eqs. (34–35) for the functions to \(\overline{u}_{z}\) and \(\overline{P}_{z}\) yields the differential equation:

$$ \left( {\frac{{d^{4} }}{{dx^{4} }} + a_{7} \frac{{d^{2} }}{{dx^{2} }} + a_{8} } \right)\left\{ {\begin{array}{*{20}c} {\overline{u}_{z} } \\ {\overline{P}_{z} } \\ \end{array} } \right. = 0, $$
(42)

with the characteristic equation

$$ \left( {\lambda^{4} + a_{7} \lambda^{2} + a_{8} } \right)\left\{ {\begin{array}{*{20}c} {\overline{u}_{z} } \\ {\overline{P}_{z} } \\ \end{array} } \right. = 0, $$
(43)

and the constants

$$ a_{7} = \frac{{a_{1} a_{6} - a_{3} a_{5} - a_{4} l_{5} }}{{a_{3} l_{5} - a_{6} }}, \quad a_{8} = \frac{{a_{2} a_{6} + a_{4} a_{5} }}{{a_{3} l_{5} - a_{6} }}. $$
(44)

The solution of the 4th order differential Eq. (39) produces four roots:

$$ \lambda_{1} = \pm \sqrt { - \frac{1}{2}\left( {a_{7} - \sqrt {a_{7}^{2} - 4a_{8} } } \right)} , \lambda_{2} = \pm \sqrt { - \frac{1}{2}\left( {a_{7} + \sqrt {a_{7}^{2} - 4a_{8} } } \right)} . $$
(45)

To guarantee that the roots \( \lambda_{1}\) and \(\lambda_{2}\) are real, the following restrictions are imposed: \(a_{7} - \sqrt {a_{7}^{2} - 4a_{8} } < 0, {\text{and}}\, a_{7} + \sqrt {a_{7}^{2} - 4a_{8} } < 0\), then the term \(a_{7}^{2} - 4a_{8}\) should be positive and, consequently, \(a_{7}\) should be less than zero:

$$ a_{7} < 0. $$

To avoid the unbounded solution, one chooses:

$$ \lambda_{1} = - \sqrt { - \frac{1}{2}\left( {a_{7} - \sqrt {a_{7}^{2} - 4a_{8} } } \right)}, \quad \lambda_{2} = - \sqrt { - \frac{1}{2}\left( {a_{7} + \sqrt {a_{7}^{2} - 4a_{8} } } \right)} , $$
(46)

the solution for the components of displacement \(u_{z}\) and polarization \(P_{z}\) are:

$$ u_{z} \left( {x,y,t} \right) = \mathop \sum \limits_{n = 1}^{2} G_{n} {\text{e}}^{{i\left( {\ell_{0} \xi y - t_{0} \omega t} \right) + \ell_{0} \lambda_{n} x}} , $$
(47)
$$ P_{z} \left( {x,y,t} \right) = \mathop \sum \limits_{n = 1}^{2} G_{n} M_{1n} {\text{e}}^{{i\left( {\ell_{0} \xi y - t_{0} \omega t} \right) + \ell_{0} \lambda_{n} x}} , $$
(48)
$$ \phi \left( {x,y,t} \right) = f_{0} {\text{e}}^{{i\left( {\ell_{0} \xi y - t_{0} \omega t} \right) - \ell_{0} \xi x}} . $$
(49)

Substituting Eqs. (42–43) into Eqs. (16–21), one gets:

$$ \sigma_{xz} = \ell_{0} \mathop \sum \limits_{n = 1}^{2} \lambda_{n} G_{n} {\text{e}}^{{i\left( {\ell_{0} \xi y - t_{0} \omega t} \right) + \ell_{0} \lambda_{n} x}} , $$
(50)
$$ \sigma_{yz} = i\ell_{0} \xi \mathop \sum \limits_{n = 1}^{2} G_{n} {\text{e}}^{{i\left( {\ell_{0} \xi y - t_{0} \omega t} \right) + \ell_{0} \lambda_{n} x}} , $$
(51)
$$ \tau_{xzx} = \mathop \sum \limits_{n = 1}^{2} \left( {\left( {l_{1} \lambda_{n}^{2} - \xi^{2} l_{7} } \right)\ell_{0}^{2} + l_{2} M_{1n} } \right)G_{n} {\text{e}}^{{i\left( {\ell_{0} \xi y - t_{0} \omega t} \right) + \ell_{0} \lambda_{n} x}} , $$
(52)
$$ \tau_{yzy} = \mathop \sum \limits_{n = 1}^{2} \left( {\left( {l_{7} \lambda_{n}^{2} - \xi^{2} l_{1} } \right)\ell_{0}^{2} + l_{2} M_{1n} } \right)G_{n} {\text{e}}^{{i\left( {\ell_{0} \xi y - t_{0} \omega t} \right) + \ell_{0} \lambda_{n} x}} , $$
(53)
$$ \tau_{xzy} = \tau_{yzx} = i\ell_{0}^{2} \xi l_{8} \mathop \sum \limits_{n = 1}^{2} \lambda_{n} G_{n} {\text{e}}^{{i\left( {\ell_{0} \xi y - t_{0} \omega t} \right) + \ell_{0} \lambda_{n} x}} , $$
(54)
$$ E_{z} = \mathop \sum \limits_{n = 1}^{2} \left( {\left( {\lambda_{n}^{2} - \xi^{2} } \right)\ell_{0}^{2} l_{5} + M_{1n} } \right)G_{n} {\text{e}}^{{i\left( {\ell_{0} \xi y - t_{0} \omega t} \right) + \ell_{0} \lambda_{n} x}} . $$
(55)

with

$$ M_{1n} = \frac{{a_{5} - \ell_{0}^{2} \lambda_{n}^{2} l_{5} }}{{a_{6} }}, n = 1,2. $$

The external force, higher-order force and surface charges are now expressed as:

$$ \begin{aligned}\sigma_{z}^{ex} &= \mathop \sum \limits_{n = 1}^{2} \left( {\ell_{0} \lambda_{n} \left( {t_{0}^{2} \omega^{2} l_{3} - 1 - \ell_{0}^{2} \xi^{2} l_{8} + \ell_{0}^{2} \left( {l_{1} \lambda_{n}^{2} - \xi^{2} l_{7} } \right) + l_{2} M_{1n} } \right)}\right. \\ & \quad \left.{ + i\ell_{0} \xi \left( {\left( {l_{7} \lambda_{n}^{2} - \xi^{2} l_{1} } \right)\ell_{0}^{2} + l_{2} M_{1n} } \right)} \right)G_{n} {\text{e}}^{{i\left( {\ell_{0} \xi y - t_{0} \omega t} \right) + \ell_{0} \lambda_{n} x}} , \end{aligned}$$
(56)
$$ \tau_{z}^{ex} = \mathop \sum \limits_{n = 1}^{2} \left( {\left( {l_{1} \lambda_{n}^{2} - \xi^{2} l_{7} } \right)\ell_{0}^{2} + l_{2} M_{1n} } \right)G_{n} {\text{e}}^{{i\left( {\ell_{0} \xi y - t_{0} \omega t} \right) + \ell_{0} \lambda_{n} x}} , $$
(57)
$$ q^{ex} = - \ell_{0} \xi f_{0} {\text{e}}^{{i\left( {\ell_{0} \xi y - t_{0} \omega t} \right) - \ell_{0} \xi x}} . $$
(58)

Applying the two boundary conditions (28–29), one obtains:

$$ W_{11} G_{1} + W_{12} G_{2} = f_{0} , $$
(59)
$$ Z_{11} G_{1} + Z_{12} G_{2} = 0, $$
(60)

With

$$ W_{11} = \left( {\delta_{1} + \ell_{0} l_{2} M_{11} + \ell_{0}^{3} l_{1} \lambda_{1}^{2} } \right)\lambda_{1} , W_{12} = \left( {\delta_{1} + \ell_{0} l_{2} M_{12} + \ell_{0}^{3} l_{1} \lambda_{2}^{2} } \right)\lambda_{2} , $$
$$ Z_{11} = l_{1} \ell_{0}^{2} \lambda_{1}^{2} - \ell_{0}^{2} \xi^{2} l_{7} + l_{2} M_{11} , Z_{12} = l_{1} \ell_{0}^{2} \lambda_{2}^{2} - \ell_{0}^{2} \xi^{2} l_{7} + l_{2} M_{12} , $$

where

$$ \delta_{1} = \left( {t_{0}^{2} \omega^{2} l_{3} - 1} \right)\ell_{0} - \left( {l_{7} + 2l_{8} } \right)\ell_{0}^{3} \xi^{2} . $$

The solution of Eqs. (53–54) yields:

$$ G_{1} = \frac{{f_{0} Z_{12} }}{{Z_{12} W_{11} - Z_{11} W_{12} }}, G_{2} = \frac{{f_{0} Z_{11} }}{{Z_{11} W_{12} - Z_{12} W_{11} }}, $$
(61)

this completely determines the closed form solution of the considered problem.

5 Numerical results and discussion

In the following subsections, we investigate the effect of three material parameters: the phenomenological parameter controlling the polarization, the flexoelectric coupling constant and the micro-inertia parameter on the behavior of the solution.

5.1 Material parameters

The Strontium Titanate (SrTiO3), or STO [45] is chosen as material. Its material coefficients are listed in the Table below (Table 1):

Table 1 Material parameters for STO
Full size table

5.2 Effect of the phenomenological constant \(\widetilde{{\varvec{\zeta}}}\)

In this part, we study the effect of the phenomenological tensor \(\widetilde{{\varvec{\zeta}}}\) controlling the dynamics of polarization. Three values are taken for this parameter: \(\widetilde{{\varvec{\zeta}}}=\left(1, 3, 5\right)\times {10}^{-16}.\) The following figures are obtained (Fig. 1).

Fig. 1
figure 1

Schematic representation of the anti-plane problem shear problem for flexoelectric material, where a line wave force is applied at the \(y\) axis

Full size image

At first, we look at the behavior of the solution at a fixed spatial location for which the coordinates \(\left(x,y\right)\) take the values \(\left(\mathrm{1,1}\right)\), while time runs from \(0 \,sec\), to \(30 \,sec\), \({\ell}_{0}=10 \,nm\), and \(h=10\, nm\). Figures 2 and 3 show that the damping in time of both the polarization and the electric field is stronger as parameter \(\widetilde{\zeta }\) assumes larger values. All the curves corresponding to the different values of the parameter seem to intersect the x-axis at common points, meaning that the speed of wave propagation is independent of the value taken by this parameter. Figures 4 and 5 show 3D-plots for the damped propagation of polarization and electric field with the \(x\)-coordinate and time for a given value of the parameter \(\widetilde{\zeta }\).

Fig. 2
figure 2

Propagation of the polarization wave \({P}_{z}\left(\mathrm{1,1},t\right)\) with time induced inside the medium, and of the electric field wave \({E}_{z}\left(\mathrm{1,1},t\right)\) measured at the surface of the medium for three values of parameter \(\widetilde{{\varvec{\zeta}}}\)

Full size image
Fig. 3
figure 3

Propagation of the polarization wave \({P}_{z}\left(x,\mathrm{1,1}\right)\) with \(x\)-coordinate induced inside the medium, and of the electric field wave \({E}_{z}\left(x,\mathrm{1,1}\right)\) measured at different \(x\)-coordinates at the surface of the medium for three values of parameter \(\widetilde{{\varvec{\zeta}}}\)

Full size image
Fig. 4
figure 4

Propagation of polarization wave \({P}_{z}\left(x,1,t\right)\) induced inside the medium

Full size image
Fig. 5
figure 5

Propagation of electric wave \({E}_{z}\left(x,1,t\right)\) measured at surface of the medium

Full size image

5.3 Effect of the flexocoupling constant \(\widetilde{{\varvec{m}}}\)

Here we study the effect of decreasing the order of the dynamic flexocoupling tensor \(\widetilde{{\varvec{m}}}\), for which three values are taken: \(\widetilde{{\varvec{m}}}=67.5\times \left({10}^{-15}, {10}^{-16}, {10}^{-17}\right).\) The following figures are obtained:

In contrast to the effect of the phenomenological parameter treated above, Figs.  6 and 7 illustrate the stronger damping effect with time of polarization and electric field as parameter \(\widetilde{m}\) decreases. Again, there is no tangible effect of this parameter on the speed of the wave.

Fig. 6
figure 6

Propagation of the polarization wave \({P}_{z}\left(\mathrm{1,1},t\right)\) with time induced inside the medium, and of the electric field wave \({E}_{z}\left(\mathrm{1,1},t\right)\) measured at the surface of the medium for three values of parameter \(\widetilde{m}\)

Full size image
Fig. 7
figure 7

Propagation of the polarization wave \({P}_{z}\left(x,\mathrm{1,1}\right)\) with \(x\)-coordinate induced inside the medium, and of the electric field wave \({E}_{z}\left(x,\mathrm{1,1}\right)\) with \(x\)-coordinate at the surface of the medium for three values of parameter \(\widetilde{{\varvec{m}}}\)

Full size image

Figures 8 and 9 are 3D-representations of the damped propagation of polarization and electric field.

Fig. 8
figure 8

Propagation of polarization wave \({P}_{z}\left(x,1,t\right)\) induced inside the medium

Full size image
Fig. 9
figure 9

Propagation of electric wave \({E}_{z}\left(x,1,t\right)\) measured at surface of the medium

Full size image

5.4 Effect of the micro-inertia term

In this part, we consider the following values for coordinates and parameters to study the effect of the micro-inertia term on the propagation of the mechanical wave and the electrical wave. For this, one takes \(x=10, y=0, 0\le t\le 25\), and the characteristic length scale parameter \({\ell}_{0}=10\). Besides, the computations are carried out for different values for the ratio \(h/{\ell}_{0}=0, 5, 10\).

Figures 10, 11, 12, 13, 14 and 15 depict 2D-variations of the state variables \({u}_{z}\), \({P}_{z}\) and \({E}_{z}\) with time and \(x\)-direction, respectively, for three different values of the ratio \(h/{\ell}_{0}\). Here one clearly sees that the speed of wave propagation increases as this ratio is larger.

Fig. 10
figure 10

Propagation of the displacement, polarization, and electric waves with time for three values of the ratio \(h/{\ell}_{0}=0, 5, 10.\)

Full size image
Fig. 11
figure 11

Propagation of the classical Cauchy stress tensor components with time for three values of the ratio \(h/{\ell}_{0}=0, 5, 10\)

Full size image
Fig. 12
figure 12

Propagation of the higher-order stress tensor components relative to time for three values of the ratio \(h/{\ell}_{0}=0, 5, 10\)

Full size image
Fig. 13
figure 13

Propagation of the displacement, polarization and electric waves with \(x\)-coordinate for three values of the ratio \(h/{\ell}_{0}=0, 10, 20.\)

Full size image
Fig. 14
figure 14

Propagation of the classical Cauchy stress tensor components with \(x\)-coordinate for three values of the ratio \(h/{\ell}_{0}=0, 10, 20.\)

Full size image
Fig. 15
figure 15

Propagation of the higher-order stress tensor components with \(x\)-coordinate for three values of the ratio \(h/{\ell}_{0}=0, 10, 20\)

Full size image

The following 3D-plots illustrate the damped propagation of some physical quantities at a point of application of the external force for three values of the ratio \(h/{\ell}_{0}\).

Figures 16 and 17 illustrate that the variations of \({u}_{z}\left(x,0,t\right)\) and \({P}_{z}\left(x,0,t\right)\) with the increase of the ratio \(h/{\ell}_{0}\) and in increasing in \(x-\) direction.

Fig. 16
figure 16

Propagation of the displacement wave in 3D at \(y=0\) for three values of the ratio \(h/{\ell}_{0}=0, 10, 20\)

Full size image
Fig. 17
figure 17

Propagation of the polarization wave in 3D at \(y=0\) for three values of the ratio \(h/{\ell}_{0}=0, 10, 20\)

Full size image

At all the considered locations, and at all computed time moments, the presented 2D-curves show damping with time and with the \(x\)–coordinate as should be. Moreover, the following interesting relation seems to hold almost exactly between the normal components of the electric field and the polarization vectors:

$${P}_{z}={-E}_{z}.$$

Referring to Eq. (21), this relation can hold only if the Laplacian of the normal mechanical displacement (multiplied by the non-vanishing factor \({l}_{5}\)) is a multiple of the electric field normal component. It is believed that such a relation is a direct consequence of the two-dimensional setting presently used Figs. 18, 19, 20.

Fig. 18
figure 18

Propagation of the electric field wave in 3D at \(y=0\) for three values of the ratio \(h/{\ell}_{0}=0, 10, 20\)

Full size image
Fig. 19
figure 19

Propagation of the Cauchy stress component \({\sigma }_{xz}\left(x,t\right)\) wave in 3D at \(y=0\) for three values of the ratio \(h/{\ell}_{0}=0, 10, 20.\)

Full size image
Fig. 20
figure 20

Propagation of the Cauchy stress component \({\sigma }_{yz}\left(x,t\right)\) wave in 3D at \(y=0\) for three values of the ratio \(h/{\ell}_{0}=0, 10, 20\)

Full size image

6 Concluding remarks

The Flamant–Boussinesq problem with dynamical flexoelectric effect for a half-space made of a homogeneous and isotropic dielectric material has been investigated. The half-space is subjected to a dynamic anti-plane wave applied at its surface. The strain gradient theory of elasticity is used as a framework for the study. Another coupling was considered with a new material parameter to control the dynamical polarization and displacement field. The solution of the studied model employed the harmonic wave solution method to obtain a bounded solution to the descriptive functions of the problem. Comparison between the responses of dielectric material to different cases of the material parameters is carried out. It is found that the micro-inertia term has a good significant effect on the wave propagation of physical fields [26]. Also, the effect of the two parameters \(\tilde{\upzeta }\) and \(\widetilde{\mathrm{m}}\) is investigated upon the electrical state variables induced inside the medium and at the surface of the half-space. All the internal states propagate as damped waves. The present results provide a physical insight in modeling the size-dependent electromechanical coupling in multifunctional materials [48], smart materials, systems, and devices for applications in sensors [49], actuators [49], nanogenerators [50], active controllers [51], nanorobotics and energy harvesters [52, 53]. It is believed that the presented results concerning the effect of the different physical parameters of the medium can be used in many applications, in medical apparatus such as blood pumps, to control the evolution of the mechanical and electrical status of the medium.