1 Introduction

Rigid heat conductors are classified as metal and nonmetal conductors. Examples of metal conductors are copper, aluminum, silver, and gold. Nonmetal conductors are metalloid, grease and graphite. The uses of thermal conductors in life manifests via a catenary, which is a system of overhead wires that supply electricity to a locomotive, streetcar or light rail vehicle. The study of heat wave propagation in continuous media has found growing interest in the past few studies. Such models have helped revealing interesting phenomena with practical applications in media of complex structure in which nonlinearity is tightly linked to stability in working conditions. Coleman and Newman [1] studied the implications of introducing a squared heat flux term in the free energy of the system, by which the heat flux and the temperature are treated as independent thermodynamical variables. Tarabek [2] investigated the existence of smooth solutions in one-dimensional nonlinear thermoelasticity with second sound, while Messaoudi et al. [3] considered the blow up of solutions in such systems. Ghaleb [4] and Gorgi and Montanaro [5] discussed models of nonlinear thermo-electroelasticity. Ghaleb et al. [6] proposed a model of nonlinear thermo-electroelasticity with many nonlinearities in extended thermodynamics, following Coleman. This model electroelasticity was further investigated by Abou-Dina and Ghaleb [7]. Rawy [8] discussed a restriction of this model to thermoelasticity. Shakeriaski and Ghodrat [9] studied the response of a thermoelastic material under a laser pulse in extended thermodynamics. Mahmoud et al. [10] studied nonlinear heat wave propagation in a rigid thermal conductor. In [10], solutions were obtained by different methods, and the effect of various material parameters was considered. Here is a variety of techniques which are used to find the exact solutions of nonlinear partial differential equations. Among them, the tanh and extended tanh methods [11, 12]. In [11], the extended tanh method is used to derive new soliton solutions for several forms of the fifth-order nonlinear KdV equation, Lax, Sawada–Kotera, Sawada–Kotera–Parker–Dye, Kaup–Kupershmidt, Kaup–Kupershmidt–Parker–Dye, and the Ito equations. Traveling wave solutions are obtained by using the modified extended tanh method for space-time fractional nonlinear partial differential equations [12]. In [13] the exact solutions of a compound KdV–Burgers equation are obtained, where in [14] the solitary wave solutions of the approximate equations for long water waves, the coupled KdV equations, and the dispersive long wave equations in 2 + 1 dimensions are constructed by using a homogeneous balance method. In [15] explicit formalisms for deep reductions of matrix differential equations and Darboux covariance properties are presented to explicit formulas of N-soliton solutions. In [16] Darboux transformation yields the variable separable solutions with two space-variable separated functions to find a new saddle-type ring soliton solution with completely elastic interaction and nonzero phase shifts. In [17] the \(\grave{G}/G\)-expansion method is proposed and used to obtain the (TWS) involving parameters of the KdV equation, the mKdV equation, a variant of Boussinesq equations, and the Hirota–Satsuma equations. In [18] a generalized \(\grave{G}/G\)-expansion method is proposed to seek exact solutions of the Benjamin–Bona–Mahony equation, (2+1)-dimensional generalized Zakharov–Kuznetsov equation, and a variant of Bousinessq equations. Triangular periodic wave solutions, hyperbolic function solutions, and Jacobian elliptic function solutions can be obtained as well. Moreover, it can also be used for many other nonlinear evolution equations in mathematical physics.

Here, the exact solutions are found by the unified method (UM) [19]. It has wide applications in investigating the behavior of the propagation of waves in shallow or in deep water. Solitary waves are also produced in compensated semiconductors [20] for determining the structure of pulse propagation in optical fibers. Also, solitary wave conduction appears in superionic conductors [21]. The (UM) covers most of all known methods in the literature such as the tanh, modified, and extended versions, the F-expansion, the exponential, and the \(\grave{G}/G\)-expansion method [22,23,24,25,26]. The extended unified method [27] proposed by the first author may be sufficient to replace the analysis of inspecting the symmetries of partial differential equations that result when using Lie groups.

In the present work, we investigate a one-dimensional nonlinear system of two partial differential equations describing the propagation of heat waves in an infinite rigid thermal conductor. In these equations, the basic unknowns are the temperature and the heat flux. Dependence of the wave speed on the unknowns is taken in consideration. A multitude of wave solutions is obtained and illustrated graphically. This may be of interest in studying such materials in working conditions.

In view of the nonlinearity of the governing equations, we have restricted our considerations to the Cattaneo–Vernotte model, i.e., a model containing only one thermal relaxation time. However, inclusion of more than one thermal relaxation time is also possible, and will be dealt with in future work. Such complicated models provide better description of the physics, but involve more mathematical difficulties [28, 29]. The model used in this work finds application in the continuum description of media with complex structure [30].

2 The model equation

Recently, a one-dimensional system of equations has been presented in [10] for the propagation of heat waves in rigid thermal conductors. The main characteristic of the model is nonlinearity of the equations arising from two sources:

  1. (i)

    the presence of a quadratic dependence of the free energy on heat flux.

  2. (ii)

    the dependence of the thermal relaxation time and the coefficient of heat conduction on temperature and heat flux. It reads,

$$\begin{aligned} \begin{array}{c} (1+\theta )\theta _{t}+\eta _{1}(Q_{x}-Q\,\theta _{x}-\eta \,Q^{2})=0,\\ \\ (1+(1+\mu _{1})\theta +\mu _{2}Q)Q_{t}+\frac{1}{\eta _{1}}(\eta \,Q+Q_{x}+\eta _{2}\theta \,\theta _{x}+\eta _{3}Q\,\theta _{x})=0. \end{array} \end{aligned}$$
(1)

In Eq. (1), all symbols are dimensionless

Table 1 List of symbols
Full size table

There, \(\eta =\frac{\mathrm{L}_{0}\mathrm{Q}_{0}}{\theta _{0}K_{0}}\), \(\eta _{1}=\frac{Q_{0}\sqrt{\tau _{0}}}{\sqrt{\Theta _{0}CK_{0}}}\), \(\eta _{2}=\frac{K_{1}}{K_{0}},\) \(\eta _{3}=\frac{K_{2}}{K_{0}}\). Here we are interested in studying the traveling waves solution (TWS) of Eq. (1). To this issue, we introduce the transformations \(\theta (x,t)=\psi (z),\;Q(x,t)=\varphi (z),\;z=\alpha \,x+\beta \,t.\) Thus, Eq. (1) reduces to,

$$\begin{aligned} \begin{array}{c} \begin{array}{c} \beta (\psi +1)\psi '-\eta _{1}\left( \eta \varphi {}^{2}-\alpha \varphi '+\alpha \varphi \,\psi '\right) =0,\\ \\ \end{array}\\ \varphi \left( \eta +\beta \eta _{1}\mu _{2}\varphi '+\alpha \eta _{3}\psi '\right) +\varphi '\left( \alpha +\beta \eta _{1}\left( \left( \mu _{1}+1\right) \psi +1\right) \right) +\alpha \eta _{2}\psi \,\psi '=0, \end{array} \end{aligned}$$
(2)

together with the boundary conditions \(\varphi (\infty )=A_{1}\), \(\psi (\infty )=B_{1}\), \(\varphi (-\infty )=A_{2},\psi (-\infty )=B_{2},\) where \(A_{i}\) and \(B_{i}\) are given in the parameters \(\alpha ,\beta ,\mu _{1},\eta _{i},i=1,2,3.\)

Here, the exact solutions of Eq. (2) are found using the unified method. Which asserts that, the solutions of a nonlinear partial differential equation are expressed in polynomial or rational forms in an auxiliary function that satisfies appropriate auxiliary equations.

3 Polynomial solutions of Eq. (2)

The solutions are represented in polynomial forms as,

$$\begin{aligned} \begin{array}{c} \begin{array}{c} \begin{array}{c} \begin{array}{c} \psi (z)=\sum \limits _{i=0}^{n_{1}}\,a_{i}\,g^{i}(z),\,\;\varphi (z)=\sum \limits _{i=0}^{n_{2}}\,b_{i}\,g^{i}(z),\\ \\ \end{array}\end{array}\end{array}\\ g^{\prime }(z)=\sum \limits _{i=0}^{r}\,c_{i}\,g^{i}(z). \end{array} \end{aligned}$$
(3)

We mention that, in Eq. (3) , g(z) is the auxiliary function and the second equation is the auxiliary equation. Here, \(n_{i}\) and r are integers. The objective is to find \(n_{i}\) and r. To this end, balance of the nonlinear and higher order derivative terms is invoked. In Eq. (2), the balance is between ,\(\psi \psi ^{\prime }\)and \(\psi \varphi ^{\prime }\). By writing \(\psi \sim g^{n_{1}}\), \(\varphi \sim g^{n_{2}}\) and \(g^{\prime }\sim g^{r}\), we get \(2n_{1}+(r-1)=n_{1}+n_{2}+(r-1)\). This holds when \(n_{1}=n_{2}\) and when r is an arbitrary integer \(r=1,2,3,...\)

3.1 When \(r=2\) and \(n=2\)

In this case Eq. (3) becomes

$$\begin{aligned} \begin{array}{c} \psi (z)=a_{2}g(z)^{2}+a_{1}g(z)+a_{0},\quad \varphi (z)=b_{2}g(z)^{2}+b_{1}g(z)+b_{0},\\ \\ g^{\prime }(z)=c_{2}g(z)^{2}+c_{1}g(z)+c_{0}. \end{array} \end{aligned}$$
(4)

Inserting Eq. (4) into Eq. (2) and setting the coefficients of \(g(z)^{j},j=0,1,\ldots \), equal to zero, one gets

$$\begin{aligned} \begin{array}{c} a_{0}=\frac{a_{1}c_{0}(\alpha b_{0}{{\eta _{1}}}-\beta )-\alpha b_{1}c_{0}{{\eta _{1}}}+b_{0}^{2}\eta {{\eta _{1}}}}{a_{1}\beta c_{0}},a_{2}=\frac{a_{1}b_{1}(\alpha a_{1}c_{0}-b_{0}\eta )}{4\alpha a_{1}b_{0}c_{0}+2\alpha b_{1}c_{0}-2b_{0}^{2}\eta },\\ \\ b_{2}=\frac{4a_{1}b_{0}^{3}\eta ^{2}(\alpha a_{1}c_{0}-b_{0}\eta )}{4\alpha ^{3}{{a_{1}}}^{2}{{c_{0}}}^{3}-\alpha b_{0}^{2}c_{0}\eta ^{2}},c_{1}=\frac{b_{1}c_{0}}{b_{0}},c_{2}=\frac{4a_{1}b_{0}^{2}\eta ^{2}(\alpha a_{1}c_{0}-b_{0}\eta )}{\alpha (2\alpha a_{1}c_{0}-b_{0}\eta )(2\alpha a_{1}c_{0}+b_{0}\eta )},\\ \\ {{\eta }}_{2}=-\frac{\beta b_{2}{{\eta _{1}}}(a_{2}{{\mu _{1}}}+a_{2}-b_{2}{{\mu _{2}}})}{2\alpha {{a_{2}}}^{2}},{{\eta }}_{3}=-\frac{\beta {{\eta _{1}}}(a_{2}{{\mu _{1}}}+a_{2}-b_{2}{{\mu _{2}}})}{\alpha a_{2}}-\frac{a_{2}{{\eta }}}{b_{2}},\\ \\ \begin{array}{c} {{\mu _{1}}}=\frac{(2\alpha a_{1}c_{0}-b_{0}\eta )\left( 4\alpha ^{2}{{a_{1}}}^{2}{{c_{0}}}^{2}-\alpha a_{1}b_{0}(b_{0}+6)c_{0}\eta +b_{0}^{2}\eta ^{2}\left( 3b_{0}^{2}{{\eta }1}^{2}+b_{0}+2\right) \right) }{b_{0}^{4}\eta ^{2}{{\eta }1}^{2}(5b_{0}\eta -8\alpha a_{1}c_{0})},\\ \begin{array}{c} \\ \begin{aligned} {{\mu _{2}}}&{}=-\left( \left( b\eta -2\alpha a_{1}c_{0}\left( -8\alpha ^{3}{{a_{1}}}^{3}{{c_{0}}}^{3}-6\alpha ^{2}{{a_{1}}}^{2}(b_{0}-2)b_{0}c_{0}^{2}\eta \right. \right. \right. \\ &{}\quad \left. \left. +\alpha +a_{1}b_{0}^{2}c_{0}\eta ^{2}\left( -6b_{0}^{2}\eta _{1}^{2}+7b_{0}-6\right) +{{b_{0}}}^{3}\eta ^{3}\left( 4b_{0}^{2}{{{\eta _{1}}}}^{2}-2b_{0}+1\right) \right) \right) \\ &{}\quad \left. \big /2{{b_{0}}}^{6}\eta ^{3}{{\eta }1}^{2}(5b_{0}\eta -8\alpha a_{1}c_{0})\right) ,\,\beta =\frac{4\alpha b_{0}^{2}\eta {{{\eta _{1}}}}}{2\alpha a_{1}c_{0}-b_{0}\eta }.\\ \\ \end{aligned} \end{array} \end{array} \end{array} \end{aligned}$$
(5)

Inserting Eq. (5) into Eq. (4), we have

$$\begin{aligned} \begin{aligned} \psi (z)&=\frac{1}{P}(4a_{1}^{3}c_{0}^{3}\alpha ^{3}-12a_{1}^{2}b_{0}c_{0}^{2}\eta \alpha ^{2}-5a_{1}b_{0}^{2}c_{0}\alpha \eta ^{2}+b_{0}^{3}\eta ^{3}\\&\quad +4a_{1}^{2}b_{0}c_{0}\alpha \eta \,(2a_{1}c_{0}\alpha +b_{0}\eta )\,g(z)+4a_{1}^{2}b_{0}^{2}\eta ^{2}(a_{1}c_{0}\alpha -b_{0}\eta )g(z)^{2}),\\ P&=4a_{1}b_{0}c_{0}\alpha \,\eta \,(2a_{1}c_{0}\alpha +bo\eta ),\\ \\ \varphi (z)&=b_{0}+\frac{2b_{0}^{2}}{\alpha c_{0}}g(z)+\frac{4a_{1}b_{0}^{3}\eta ^{2}(a_{1}c_{0}\alpha -bo\eta )\,g(z)^{2}}{4a_{1}^{3}c_{0}^{3}\alpha ^{3}-b_{0}^{2}c_{0}\alpha \eta ^{2}}.\\ \end{aligned} \end{aligned}$$
(6)

The solution of the auxiliary equation is

$$\begin{aligned} \begin{array}{c} g(z)=\frac{-M_{2}M_{1}\tanh \left( \frac{\eta M_{2}\left( 4\alpha ^{2}Aa_{1}^{2}b_{0}^{2}c_{0}^{2}-Ab_{0}^{4}\eta ^{2}+c_{0}z\right) }{\alpha c_{0}\sqrt{2\alpha a_{1}c_{0}-b_{0}\eta }\,(2\alpha a_{1}c_{0}b_{0}\eta )}\right) -4\alpha ^{2}a_{1}^{2}b_{0}c_{0}^{2}+b_{0}^{3}\eta ^{2}}{4\alpha a_{1}^{2}b_{0}^{2}c_{0}\eta -4a_{1}b_{0}^{3}\eta ^{2}},\\ \\ \eta>0,\;\alpha>0,\;c_{0}>0,\;b_{0}>0,\frac{b_{0}\eta }{\;4c_{0}\alpha }<a_{1}<\frac{b_{0}\eta }{c_{0}\alpha }. \end{array} \end{aligned}$$
(7)

Inserting Eq. (7) into Eq.(6), we get

$$\begin{aligned} \begin{aligned} \theta (x,t)&=\frac{1}{4P}(b_{0}(-40a_{1}^{2}c_{0}^{2}\alpha ^{2}+34a_{1}b_{0}c_{0}\eta \alpha -3b_{0}^{2}\eta ^{2})\\&\quad -2M_{1}M_{2}\tanh \left[ \frac{(A_{0}+c_{0}z)\eta M_{2}}{c_{0}\alpha M_{1}(2a_{1}c_{0}\alpha +b_{0}\eta )}\right] +bo(8a_{1}^{2}c_{0}^{2}\alpha ^{2}\\&\quad -6a_{1}b_{0}c_{0}\eta \alpha +b_{0}^{2}\eta ^{2})\tanh \left[ \frac{(A_{0}+c_{0}z)\eta M_{2}}{c_{0}\alpha M_{1}(2a_{1}c_{0}\alpha +b_{0}\eta )}\right] ^{2},\\ \\ Q(x,t)&=\frac{(b_{0}^{2}\eta -4a1c_{0}\alpha +b_{0}\eta )sech(\frac{(A_{0}+c_{0}z)\eta M_{2}}{c_{0}\alpha M_{1}(2a_{1}c_{0}\alpha +b_{0}\eta )})^{2}}{4a_{1}c_{0}(a_{1}c_{0}\alpha -b\eta )},M_{1}=\sqrt{2a_{1}c_{0}\alpha -b_{0}\eta },\\ \;M_{2}&=\sqrt{b_{0}^{3}\eta (8a_{1}^{2}c_{0}^{2}\alpha ^{2}+2a_{1}b_{0}c_{0}\eta \alpha -b_{0}^{2}\eta ^{2})},z=\alpha \,x+\beta \,t, \end{aligned} \end{aligned}$$
(8)

and P is given by Eq. (6). Here, we focus our study on the behavior of temperature and heat flux of the material with properties given in Table 2.

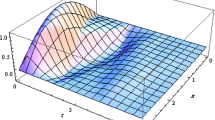
Table 2 Dimensions of the parameters
Full size table

The numerical results of the solutions in Eq. (8) for \(\theta (x,t)\) and Q(x, t) are displayed against x for different values of t in Fig. 1(i)–(ii) and (iv)–(vi), respectively. The values of \(\eta =\frac{L_{0}\phi _{0}}{\theta _{0}K_{0}},\eta _{1}=\frac{Q_{0}\sqrt{\tau _{0}}}{\sqrt{\Theta _{0}CK_{0}}}\) are taken as in [10].

Fig. 1
figure 1

(i)–(vi) When \(b_{0}=10,\,c_{0}=0.1,\,a_{1}=3,\,\alpha =2,\,A_{0}=5\). Case 1: \(\eta =0.00989078,\eta _{1}=\,1.00171\), Case 2: \(\eta =0.999621,\eta _{1}=0.999577\), Case 3: \(\eta =0.999799,\eta _{1}=1.00011\) (see Table 2)

Full size image

(i) Shows a soliton with double kinks for the temperature, which attains a steady state for large x, while it increases with time t, while (ii) shows a soliton for the heat flux.

(iii) Shows a solitary wave for the temperature, while (iv) shows a soliton for the heat flux. In (v), the behavior of the TWS of the temperature is solitary, while in (vi) it is soliton for the heat flux.

3.2 When \(r=3\) and \(n=4\)

In this case, we write,

$$\begin{aligned} \begin{array}{c} \begin{array}{c} \psi (z)=a_{4}g(z)^{4}+a_{3}g(z)^{3}+a_{2}g(z)^{2}+a_{1}g(z)+a_{0},\\ \varphi (z)=b_{4}g(z)^{4}+b_{3}g(z)^{3}+b_{2}g(z)^{2}+b_{1}g(z)+b_{0},\\ g^{\prime }(z)=(a^{2}-b^{2}g(z)^{2})g(z). \end{array}\end{array} \end{aligned}$$
(9)

Inserting Eq. (9) into Eq. (2), and by the same way as in the above, we get

$$\begin{aligned} \begin{array}{c} b_{0}=b_{1}=b_{3}=0,\;a_{1}=a_{3}=0,\\ b4=\left( b^{4}\left( M-a^{2}\left( 17a_{0}^{3}+43a_{0}^{2}+23a_{0}-3\right) \eta \right) ^{2}\right. \\ \left. a^{2}\left( 17a_{0}^{3}+43a_{0}^{2}+23a_{0}-3\right) \eta +M\right) \big /\\ \begin{array}{c} \begin{array}{c} 64a^{10}(a_{0}+2)^{2}\left( 17a_{0}^{2}+26a_{0}-3\right) ^{2}\left( 37a_{0}^{2}+98a_{0}+61\right) \eta ^{3}{{\eta _{1}}}^{4},\\ \\ \end{array}\\ b2=-\left( 3(5a_{0}+8)b^{2}\left( a^{2}\left( 17a_{0}^{3}+43a_{0}^{2}+23a_{0}-3\right) \eta -M\right) \big /\right. \\ \left. 4a^{4}(37a_{0}+61)\left( 17a_{0}^{2}+26a_{0}-3\right) \eta {{\eta _{1}}}^{2}\right) ,\\ \\ \begin{array}{c} a_{2}=\frac{3(a_{0}+1)(3a_{0}+4)b^{2}}{2a^{2}(37a_{0}+61)},a_{4}=-\frac{3(a_{0}+1)^{2}b^{4}}{2a^{4}(37a_{0}+61)},\beta {=}-\frac{\alpha {{\eta _{1}}}({{\mu _{1}}}+1)}{{{\mu _{2}}}},\\ \\ \begin{array}{c} {{\eta _{3}}}=-\frac{\beta {{\eta }1}(a_{4}{{\mu _{1}}}+a_{4}+a_{4}{{\mu _{2}}})}{\alpha a_{4}}-\frac{a_{4}{{\eta _{2}}}}{b_{4}},{{\eta _{2}}}=-\frac{\beta b_{4}{{\eta _{1}}}(a_{4}{{\mu _{1}}}+a_{4}-3b_{4}{{\mu _{2}}})}{4\alpha {{a_{4}}}^{2}},\\ \begin{array}{c} \\ \begin{array}{c} {{\mu _{1}}}=\frac{-8\alpha ^{2}a^{4}\left( a_{0}^{3}+5{{a_{0}}}^{2}+7a_{0}+2\right) {{\eta _{1}}}^{2}+\alpha a^{2}(a_{0}+1)^{2}\eta +(a_{0}+1)^{2}\eta ^{2}}{8a^{4}\alpha ^{2}a_{0}(a_{0}+2)^{2}{{\eta _{1}}}^{2}},\\ \begin{array}{c} \\ \begin{array}{c} \alpha =\frac{a^{2}\left( 17{{a_{0}}}^{3}+43{{a_{0}}}^{2}+23a_{0}-3\right) \eta -M}{16a^{4}\left( 17{{a_{0}}}^{3}+60{{a_{0}}}^{2}+49a_{0}-6\right) {{\eta _{1}}}^{2}},\beta =-\frac{\alpha {{\eta _{1}}}({{\mu _{1}}}+1)}{{{\mu }2}}.\\ \\ \end{array} \end{array} \end{array} \end{array} \end{array} \end{array} \end{array} \end{array} \end{aligned}$$
(10)

The solution of the auxiliary equation is

$$\begin{aligned} \begin{array}{c} g(z)=\frac{aA_{0}e^{a^{2}z}}{\sqrt{1+b^{2}A_{0}^{2}e^{2a^{2}z}}}.\\ \\ \end{array} \end{aligned}$$
(11)

Finally, the solutions are

$$\begin{aligned} \begin{array}{c} \theta (x,t)=a_{0}-\frac{3(a_{0}+1)^{2}A_{0}^{4}b^{4}e^{4a^{2}z}}{2(37a_{0}+61)\left( A_{0}^{2}b^{2}e^{2a^{2}z}+1\right) ^{2}}+\frac{3(a_{0}+1)(3a_{0}+4)A_{0}^{2}b^{2}e^{2a^{2}z}}{2(37a_{0}+61)\left( A_{0}^{2}b^{2}e^{2a^{2}z}+1\right) },\\ \\ \begin{array}{c} Q(x,t)=-\left( \left( 3A_{0}^{2}b^{2}e^{2a^{2}z}\left( a_{0}\left( 4A_{0}^{2}b^{2}e^{2a^{2}z}+5\right) +7A_{0}^{2}b^{2}e^{2a^{2}z}+8\right) \right. \right. \\ \begin{array}{c} \left. -\frac{M}{a^{2}\eta }+17{{a_{0}}}^{3}+43a_{0}^{2}+23a_{0}-3\right) \big /(4(37a_{0}+61)\\ \left. \left. \left( 17a_{0}^{2}+26a_{0}-3\right) \left( A_{0}^{2}b^{2}{{\eta _{1}}}e^{2a^{2}z}+{{\eta _{1}}}\right) ^{2}\right) \right) ,\;z=\alpha x+\beta t,\\ \\ \end{array}\\ M=a^{2}\eta \sqrt{-(a_{0}+1)^{2}\left( 17a_{0}^{2}+26a_{0}-3\right) \left( a_{0}^{2}\left( 48{{\eta _{1}}}^{2}-17\right) +2a_{0}\left( 96{{\eta _{1}}}^{2}-13\right) +192{{\eta }}_{1}^{2}+3\right) }. \end{array}\end{array} \end{aligned}$$
(12)

where \(b_{i},i=2,4\) are given in Eq. (10). The results of the solutions in Eq. (12) for \(\theta (x,t)\) and Q(x, t) are displayed against x for different values of t in Fig. 2(i) and (ii). We focus on case-I in Table 2 and \(\eta =\frac{L_{0}\phi _{0}}{\theta _{0}K_{0}},\eta _{1}=\frac{Q_{0}\sqrt{\tau _{0}}}{\sqrt{\Theta _{0}CK_{0}}}\).

Fig. 2
figure 2

(i) and (ii) Numerical results of the solutions in Eq. (12) for \(\theta (x,t)\) and Q(x, t) are displayed against x for different values of t when \(b_{0}=-10,\,c_{0}=0.1,\,a_{1}=3,\,\alpha =2,\,A_{0}=5\). In case-I, \(\eta =0.00989078,\eta _{1}=\,1.00171\)

Full size image
Fig. 3
figure 3

(i) and (ii) When \(\alpha =1.3,\,\beta =-2.5,\,A_{0}=-5\) and in case-I, from the Table 2, \(\eta =0.00989078,\eta _{1}=\,1.00171\) It is remarked that the temperature and heat flux increase with time

Full size image

(i) and (ii) show that the temperature and the heat flux decrease with time and attain steady states in space. The qualitative behavior is solitary wave.

4 Rational solutions of Eq. (2)

A rational solution (TWS) of Eq. (2) is written in the form

$$\begin{aligned} \begin{array}{c} \begin{array}{c} \psi (z)=\frac{a_{1}g(z)+a_{0}}{s_{1}g(z)+s_{0}},\quad \varphi (z)=\frac{b_{1}g(z)+b_{0}}{s_{1}g(z)+s_{0}},\\ \\ g^{\prime }(z)=\sum \limits _{j=0}^{j=k}c_{j}g(z)^{j}. \end{array}\end{array} \end{aligned}$$
(13)

Here, we consider two cases.

4.1 When \(k=2\)

The auxiliary equation reads

$$\begin{aligned} g^{\prime }(z)=c_{2}g(z)^{2}+c_{1}g(z)+c_{0}. \end{aligned}$$
(14)

From Eqs. (13) and (14) and insertion into Eq. (2), we have

$$\begin{aligned} \begin{aligned} c_{2}&=\frac{1}{2s_{1}},c_{1}=\frac{2\beta \,\eta \left( \sqrt{2{{\eta _{1}}}^{2}+1}{ {\eta _{1}}}^{2}-\sqrt{2{{\eta _{1}}}^{2}+1}-1\right) }{\alpha ^{2}\eta _{1}\left( 2\eta _{1}^{2}-3\right) },\,c_{0}=0\,,\\ a_{1}&=\frac{1}{c_{2}}-s_{1},\,a_{0}=\frac{4\beta \eta {{\eta _{1}}}^{3}s_{1}^{2}-\alpha ^{2}s_{0}}{\alpha ^{2}\left( \eta _{1}^{2}-1\right) },\,b_{1}=\frac{2\beta { {\eta _{1}}}s_{1}}{\alpha },\\ b_{0}&=\frac{a_{1}s_{0}(\beta -\alpha b_{1}{{c_{2}}}{{{\eta _{1}}}})+a_{0}s_{1}(\alpha b_{1}{{c_{2}}}{{{\eta _{1}}}}-\beta )+b_{1}{{\eta _{1}}}s_{1}(\alpha c_{2}s_{0}-b_{1}\eta )}{\alpha c_{2}{{\eta _{1}}}s_{1}^{2}},\\ s_{0}&=-\frac{4\left( \alpha ^{2}\beta \eta {{s_{1}}}^{2}-\alpha ^{2}\beta \eta \left( {{{{\eta _{1}}}}}^{2}-1\right) \sqrt{2{{{{\eta _{1}}}}}^{2}+1}{{s_{1}}}^{2}\right) }{\alpha ^{4}\left( 2{{{{\eta _{1}}}}}^{3}-3{{\eta _{1}}}\right) },\\ {{\eta _{2}}}&=\left( 2\alpha \beta \left( 2{{{\eta _{1}}}}^{6}-3{{\eta _{1}}}^{4}-2\sqrt{2{{\eta _{1}}}^{2}+1}{{\eta _{1}}}^{2}+2\sqrt{2{{\eta _{1}}}^{2}+1}+2\right) \right. \\&\quad +\alpha ^{2}{{\eta _{1}}}\left( 2{{\eta _{1}}}^{2}-3\right) \left( \sqrt{2{{\eta _{1}}}^{2}+1}\eta _{1}^{2}-\sqrt{2{{\eta _{1}}}^{2}+1}-1\right) +2\beta ^{2}\eta _{1}\left( 2\left( \sqrt{2{{\eta _{1}}}^{2}+1}+1\right) ({{\mu _{1}}}+2)\right. \\&\quad +\eta _{1}^{2}\left( -2\sqrt{2{{\eta _{1}}}^{2}+1}+2{{\mu _{1}}}+2\right) +2{{{\eta _{1}}}}^{6}\left( \sqrt{2{{{\eta _{1}}}}^{2}+1}+1\right. \\&\quad \left. \left. \left. \sqrt{2{{{\eta _{1}}}}^{2}+1}{{\mu _{1}}}\right) -{{{\eta _{1}}}}^{4}\left( 3\sqrt{2{{{\eta _{1}}}}^{2}+1}{{\mu _{1}}}+3\sqrt{2{{\eta _{1}}}^{2}+1}+4{{{\mu _{1}}}}+7\right) \right) \right) /\\&\alpha {{\eta _{1}}}\left( -2{{{\eta _{1}}}}^{2}+\sqrt{2{{{\eta _{1}}}}^{2}+1}+1\right) \left( -2{{{\eta _{1}}}}^{4}+{{{\eta _{1}}}}^{2}+\sqrt{2{{\eta _{1}}}+1}+1\right) ,\\ {{\eta _{3}}}&=\left( -\alpha ^{3}{{\eta _{1}}}\left( 2{{\eta _{1}}}^{2}-3\right) \left( -2{{{\eta _{1}}}}^{2}+\sqrt{2{{\eta _{1}}}^{2}+1}+1\right) \right. +2\alpha ^{2}\beta \left( 2\left( \sqrt{2{{{{\eta _{1}}}}}^{2}+1}-1\right) {{\eta _{1}}}^{4}+2\left( \sqrt{2{{{{\eta _{1}}}}}^{2}+1}+1\right) \right. \\&\quad \left. -{{{{\eta _{1}}}}}^{2}\left( 3\sqrt{2{{{\eta _{1}}}}^{2}+1}+1\right) \right) +2\alpha \beta ^{2}{{{{\eta _{1}}}}}\left( 2{{{{\eta _{1}}}}}^{4}\left( \sqrt{2{{{{\eta _{1}}}}}^{2}+1}-1\right) \right. \left. +2\left( \sqrt{2{{{{\eta _{1}}}}}^{2}+1}+1\right) -{{{{\eta _{1}}}}}^{2}\left( 3\sqrt{2{{{{\eta _{1}}}}}^{2}+1}+1\right) \right) \\&\quad +4\beta ^{3}\left( 2\sqrt{2{{{\eta _{1}}}}^{2}+1}{{{{\eta _{1}}}}}^{6}+2{{{{\eta _{1}}}}}^{2}+2\left( \sqrt{2{{{\eta _{1}}}}^{2}+1}+1\right) \right. \\&\quad \left. \left. -{{{{\eta _{1}}}}}^{4}\left( 3\sqrt{2{{{{\eta _{1}}}}}^{2}+1}+4\right) \right) \mu _{2}\right) /\left( 2\alpha ^{2}\beta \left( -2{{{{\eta _{1}}}}}^{2}+\sqrt{2{{{{\eta _{1}}}}}^{2}+1}+1\right) -2{{{{\eta _{1}}}}}^{4}+{{{{\eta _{1}}}}}^{2}+\sqrt{2{{{{\eta _{1}}}}}^{2}+1}+1\right) . \end{aligned} \end{aligned}$$
(15)

The solution of the auxiliary equation gives rise to

$$\begin{aligned} \begin{aligned} g(z)&=-\frac{1}{\alpha ^{2}\eta _{1}(-3+2\eta _{1}^{2})}(2s_{1}\beta \,\eta \,\left( -1+\sqrt{1+2\eta _{1}^{2}}(-1+\eta _{1}^{2})\right) \\&\quad (1+\tanh ((Ao+z)\,\beta \,\eta \,\left( -1+\sqrt{1+2\eta _{1}^{2}}(-1+\eta _{1}^{2}))\right) . \end{aligned} \end{aligned}$$
(16)

Finally the solutions are

$$\begin{aligned} \theta (x,t)= & {} \frac{P_{1}}{R_{1}},\quad P_{1}=1-4\eta _{1}^{4}+\sqrt{1+2\eta _{1}^{2}}\,(1+\eta _{1}^{2})+2\eta _{1}^{2}+(-1+\sqrt{1+2\eta _{1}^{2}}\nonumber \\&\qquad \qquad \left( -1+\eta _{1}^{2})\right) \,\left( 1+\tanh ((A_{0}+\alpha x+\beta t)\,\beta \,\eta \,\left( -1+\sqrt{1+2\eta _{1}^{2}}(-1+\eta _{1}^{2})\right) \right) ,\nonumber \\ R_{1}= & {} \left( -1+\sqrt{1+2\eta _{1}^{2}}(-1+\eta _{1}^{2})\right) \left( -1+\tanh ((A_{0}+\alpha x+\beta t\right) \nonumber \\&\begin{array}{c} \beta \eta \,\left( -1+\sqrt{1+2\eta _{1}^{2}}(-1+\eta _{1}^{2}))\right) ,\\ \begin{array}{c}\\ Q(x,t)=\frac{2\beta \eta _{1}\left( \tanh \left( \frac{\beta \eta \left( \sqrt{2\eta _{1}^{2}+1}{{\eta _{1}}}^{2}-\sqrt{2\eta _{1}^{2}+1}-1\right) (A_{0}+z)}{\alpha ^{2}\eta _{1}\left( 2\eta _{1}^{2}-3\right) }\right) +1\right) }{\alpha \left( \tanh \left( \frac{\beta \eta \left( \sqrt{2\eta _{1}^{2}+1}{{\eta _{1}}}^{2}-\sqrt{2\eta _{1}^{2}+1}-1\right) (A_{0}+z)}{\alpha ^{2}{{\eta _{1}}}\left( 2\eta _{1}^{2}-3\right) }\right) -1\right) },\;z=\alpha x+\beta t. \end{array} \end{array} \end{aligned}$$
(17)

The numerical results of the solutions in Eq. (17) for \(\theta (x,t)\) and Q(x, t) are displayed against x for different values of t in Fig. 3(i) and (ii), respectively.

4.2 When \(k=2\)

Here, we take the auxiliary equation

$$\begin{aligned} g^{\prime }(z)=a-bg(z)^{2}. \end{aligned}$$
(18)

By the same way, we have

$$\begin{aligned} \begin{array}{l} a=\frac{bs_{1}^{2}}{s_{0}^{2}}\;b_{1}=-\frac{b_{0}s_{1}}{s_{0}},\\ a_{1}=\frac{s_{1}\left( a_{0}^{2}b\beta s_{0}+a_{0}bs_{0}(\beta s_{0}-\alpha b_{0}{{\eta }1})+b_{0}{{\eta _{1}}}\left( 2\alpha b{{s_{0}}}^{2}+b_{0}\eta s_{1}\right) \right) }{b{{s_{0}}}^{2}(a_{0}\beta -\alpha b_{0}{{\eta _{1}}}+\beta s_{0})},\\ a_{0}=\frac{1}{2bs_{1}s_{0}\beta ^{2}\eta }(-2b^{2}s_{0}^{3}\alpha ^{2}\beta \eta _{1}+bs_{1}s_{0}\beta \eta (-2s_{0}\beta +b_{0}\alpha \eta _{1})+H),\\ \begin{array}{l} \eta _{2}=\left( 2bs_{0}a_{0}\beta -\alpha b_{0}{{\eta _{1}}}+\beta s_{0}\left( 2{{a_{0}}}^{2}b\beta ^{2}{{\eta _{1}}}({{\mu }1}+1)s_{0}\right. \right. \\ \eta +s_{1}\left( \beta b_{0}^{2}{{\eta _{1}}}^{2}({{\mu _{1}}}+1)+\alpha b_{0}{{\eta _{1}}}s_{0}-\beta {{s_{0}}}^{2}\right) +2bs_{0}^{2}(\beta s_{0}\\ (\alpha +\beta {{\eta _{1}}})+\alpha b_{0}{{\eta _{1}}}(\beta {{\eta _{1}}}{{\mu _{1}}}-\alpha ))+a_{0}\beta s_{0}\\ \left. \left. -2\alpha bb_{0}{{\eta _{1}}}^{2}({{{\mu _{1}}}}+1)+2bs_{0}(\alpha +\beta {{\eta _{1}}}({{{\mu _{1}}}}+2))-\eta {{s_{1}}}\right) \right) \Bigg /\\ \begin{array}{l} \left( \alpha 2\alpha bs_{0}^{2}+b_{0}\eta s_{1}\eta _{1}\left( 2{{a_{0}}}^{2}b\beta s_{0}\right. \right. \\ \left. \left. 2a_{0}bs_{0}(\beta s_{0}-\alpha {{b_{0}}}\eta _{1})+b_{0}{{\eta _{1}}}\left( 2\alpha b{{s_{0}}}^{2}+b_{0}\eta s_{1}\right) \right) \right) ,\\ \\ \eta _{3}=\left( s_{0}a_{0}\beta -\alpha {{b_{0}}}\eta _{1}+\beta s_{0}\left( 2b\eta s_{1}-b_{0}\eta ^{2}s_{1}^{2}\right. \right. \\ \begin{array}{l} \beta {{b_{0}}}^{2}{{\eta _{1}}}{{\mu _{2}}}+b_{0}s_{0}(\alpha +\beta {{\eta _{1}}})- \alpha {{s_{0}}}^{2}+4b^{2}s_{0}\left( \alpha {{s_{0}}}^{2}(\alpha +\beta {{\eta _{1}}})\right. \\ +a_{0}\beta {{\mu _{2}}}(a_{0}\beta -\alpha b_{0}\eta _{1})+\beta {{\mu _{2}}}s_{0}(a_{0}\beta +\alpha b_{0}{{\eta _{1}}}))))/\\ \left( \alpha ^{2}\alpha b{{s_{0}}}^{2}+b_{0}\eta s_{1}\left( 2a_{0}^{2}b\beta s_{0}+b_{0}\right. \right. \\ \left. \left. 2a_{0}bs_{0}(\beta s_{0}-\alpha b_{0}{{\eta _{1}}})+{{\eta _{1}}}\left( 2\alpha b{{s_{0}}}^{2}+b_{0}\eta s_{1}\right) \right) \right) ,\\ \\ \end{array} \end{array} \end{array}\\ H=(2bs_{0}^{2}\alpha +b_{0}s_{1}\eta )\sqrt{bs_{1}s_{0}\beta ^{2}\eta _{1}}\sqrt{-2s_{1}\beta \eta +bs_{0}\alpha ^{2}\eta _{1}}~{^{.}} \\ \end{array} \end{aligned}$$
(19)

Finally, the solutions are,

$$\begin{aligned} \begin{array}{l} \theta (x,t)=\left( 2\alpha ^{2}b^{2}\beta \eta {{\eta _{1}}}s_{1}{{s_{0}}}^{3}(\alpha b_{0}{{{\eta _{1}}}}-\beta s_{0})+4\alpha ^{4}b^{3}\beta {{{\eta _{1}}}}^{2}s_{0}^{5}\right. \\ \alpha (-b){{{\eta _{1}}}}{{s_{0}}}^{2}\left( 3\beta ^{2}{{b_{0}}}\eta ^{2}s_{1}^{2}+2\alpha H\right) +\beta \eta (-s_{1})\left( \beta {{b_{0}}}^{2}\eta ^{2}{{{\eta _{1}}}}{{s_{1}}}^{2}+Hs_{0}\right) \\ +\left( 2\alpha ^{2}b^{2}\beta \eta {{{\eta _{1}}}}s_{1}{{s_{0}}}^{3}(\beta s_{0}-\alpha {{b_{0}}}{{{\eta _{1}}}})-4\alpha ^{4}b^{3}\beta {{{\eta _{1}}}}^{2}{{s_{0}}}^{5}\right. \\ \begin{array}{c} \left. \alpha b{{\eta _{1}}}{{s_{0}}}^{2}\left( 2\alpha H-\beta ^{2}{{b_{0}}}\eta ^{2}{{s_{1}}}^{2}\right) +\beta \eta (+s_{1})\left( Hs_{0}-\beta {{b_{0}}}^{2}\eta ^{2}{{\eta _{1}}}{{s_{1}}}^{2}\right) \right) \\ \left. \tanh \left( \frac{{{s_{0}}}(A_{0}-bz)}{s_{1}}\right) \right) /\left( s_{1}s_{0}\beta \eta \left( 2\alpha ^{2}b^{2}\beta {{{\eta _{1}}}}{{s_{0}}}^{3}\right. \right. \\ \left. \alpha +b\beta b_{0}\eta {{{\eta _{1}}}}s_{1}{{s_{0}}}-H)\tanh \left( \frac{{{s_{0}}}({{A_{0}}}-bz)}{s_{1}}\right) -1\right) ,\\ \\ Q(x,t)=\frac{b_{0}(1+\tanh (\frac{s_{0}(A_{0}-bz)}{s_{1}})}{s_{0}(-1+\tanh (\frac{s_{0}(A_{0}-bz)}{s_{1}})},\;z=\beta t+\alpha x. \end{array}\\ \\ \end{array} \end{aligned}$$
(20)

The numerical results of the solutions in Eq. (20) for \(\theta (x,t)\) and Q(x, t) are displayed against x for different values of t in Fig. 4(i) and (ii), respectively. (i) and (ii) show that the temperature and heat flux increase with time.

Fig. 4
figure 4

(i) and (ii). When \(A_{0}=-5,b=0.07,s_{1}=2.5,s_{0}=1.5,b_{0}=5,\alpha =1.5,\beta =-1.5,\) and \(\eta =0.00989078,\eta _{1}=\,1.00171\)

Full size image

It is worthy to mention that the role of varying the parameters \(\eta _{2},\,\eta _{3}\), and \(\mu _{2}\) is considered, but we have observed that there is no significant contribution. So, the figures were omitted.

5 Stability analysis

Here, we analyze the stability of the steady state solutions of Eq. (1). The steady state solutions hold by setting \(\theta _{t}=0\) and \(Q_{t}=0\), where \(\theta (x,t)=h(x)\) and \(Q(x,t)=p(x),\) which satisfy the equations

$$\begin{aligned} \begin{array}{c} -\eta p(x)^{2}-p(x)h^{\prime }(x)+p^{\prime }(x)=0,\\ \\ \eta _{2}h(x)h^{\prime }(x)]+p(x)\eta +\eta _{3}h^{\prime }(x))+p^{\prime }(x)=0. \end{array} \end{aligned}$$
(21)

The solutions are \(p(x)=0,\,h(x)=h_{0}\).

We write

$$\begin{aligned} \theta (x,t)=h_{0}+\varepsilon _{1}e^{\lambda t}H(x),\quad Q(x,t)=\varepsilon _{2}e^{\lambda t}K(x). \end{aligned}$$
(22)

Substituting Eq. (22) into Eq. (1), we get

$$\begin{aligned} \begin{array}{c} \begin{array}{c} M\left( \begin{array}{c} \varepsilon _{1}\\ \varepsilon _{2} \end{array}\right) =0,\quad M=\left( \begin{array}{c@{\quad }c} m_{11} &{} m_{12}\\ m_{21} &{} m_{22} \end{array}\right) ,\\ \\ \end{array}\\ m_{11}=\lambda h(x)H(x)-{{\eta _{1}}}p(x)H'(x)+\lambda H(x),\\ \\ m_{12}=-{{\eta _{1}}}h'(x)K(x)-2\eta {{\eta _{1}}}p(x)K(x)+{{\eta _{1}}}K'(x),\\ \\ m_{21}={{\eta _{2}}}H(x)\,h'(x)+{{\eta _{2}}}h(x)\,H'(x)+{{\eta _{3}}}p(x)\,H'(x),\\ \\ \begin{array}{l} m_{22}=\frac{{{\eta _{3}}}h'(x)K(x)}{{{\eta _{1}}}}+\lambda {{\mu _{1}}}h(x)K(x)+\lambda h(x)K(x)\\ \qquad \qquad +\lambda {{\mu _{2}}}p(x)K(x)+\frac{\eta \,K(x)}{{{\eta _{1}}}}+\lambda K(x)+\frac{K'(x)}{{{\eta _{1}}}}, \end{array} \end{array} \end{aligned}$$
(23)

which gives rise

$$\begin{aligned} \begin{array}{c} {{\eta _{1}}}\left( {{{\eta _{2}}}}H(x)h'(x)+H'(x)({{{\eta _{2}}}}h(x)+{{\eta _{3}}}p(x))\right) \left( K(x)\left( h'(x)+2\eta p(x)\right) -K'(x)\right) \\ +\frac{1}{{{\eta _{1}}}}[\lambda (h(x)+1)\,H(x)-{{\eta _{1}}}p(x)H'(x)(K(x)(\eta +{{\eta _{1}}}\lambda +{{\eta _{1}}}\lambda \\ \left. \left. {{{\eta _{3}}}}h'(x)+({{{\mu _{1}}}}+1)h(x)+{{\eta _{1}}}\lambda {{{\mu _{2}}}}p(x)\right) +K'(x)\right) ]=0.\\ \\ \end{array} \end{aligned}$$
(24)

The eigenvalue problem in Eq. (24) is subjected to the boundary conditions (BCs) \(H(\pm \infty )=0\) and \(K(\pm \infty )=0.\) To this issue, we assume that

$$\begin{aligned} \begin{array}{c} H(x)=H_{0}{\left\{ \begin{array}{ll} e^{-m\,x} &{} m>0,\,x>0\\ e^{m\,x} &{} m>0,\,x<0, \end{array}\right. }\\ \\ K(x)=K_{0}{\left\{ \begin{array}{ll} e^{-m\,x} &{} m>0,\,x>0\\ e^{m\,x} &{} m>0,\,x<0. \end{array}\right. } \end{array} \end{aligned}$$
(25)

Substituting Eq. (25) into Eq. (24), we have,

$$\begin{aligned} \lambda =\frac{-\eta -\eta h_{0}\pm \sqrt{(h_{0}+1)\left( 4{{\eta _{1}}}^{3}{{\eta _{2}}}h_{0}m^{2}(h_{0}{{\mu _{1}}}+h_{0}+1)+(h_{0}+1)(m-\eta )^{2}\right) }+h_{0}m+m}{2{{\eta _{1}}}(h_{0}+1)(h_{0}{{\mu _{1}}}+h_{0}+1)}. \end{aligned}$$
(26)

We mention that the steady state solution is saddle node. The results in (26) are shown in Fig. 5 (i) and (ii).

Fig. 5
figure 5

(i), (ii)  and (ii), Eigenvalue \(\lambda \) against \(\eta ,\eta _{1}\), and m, respectively . When (i) \(h_{0}=2,m=0.5,{{\mu _{1}}}=0.3,{{\eta _{1}}}=0.1,{{\eta _{2}}}=0.1,\) (ii) \(h_{0}=2,m=0.5,{{\mu _{1}}}=0.3,\eta =0.5,{{\eta _{2}}}=1\), and (iii) \(h_{0}=0.2,\eta =0.5,{{\eta _{1}}}=0.2,{{\eta _{2}}}=0.1,{{\mu _{1}}}=0.3.\)

Full size image
  1. (i)

    the solutions are stable or unstable, and the point at \(m=0.5\) is a saddle point.

  2. (ii)

    the solutions are stable or unstable with critical point \(\eta _{1}=0.01\).

  3. (iii)

    when \(m>0.5\) the solutions are stable, when \(m<0.5\) the solutions are stable or unstable and the point at \(m=0.5\) is a saddle point.

6 Conclusions

The temperature–heat flux model equation for nonlinear heat waves in a rigid conductor is considered. Exact traveling waves solutions are found using the (UM). The results are illustrated in a variety of graphs. It is found that nonlinear heat waves are solitary waves. The attained states in space and the temperature and heat flux increase with time. The effects of the characteristic parameters, length, time, and heat flux are investigated and shown in a graph. It is found that the solutions are solitary, soliton, or soliton with double kinks. It is remarked that the stability of the solutions depends critically on the wave number of the perturbed solutions with a critical value, above it the solutions are stable. Otherwise they are unstable.

In view of the nonlinearity of the governing equations, considerations were confined to a single thermal phase lag. Cases with more than one thermal relaxation time will be considered in future work.