1 Introduction

1.1 Background

Under the cyclic loading, elastoplastic materials indicate different mechanical responses associated with the plastic deformation  [1, 2]. Ratcheting, Bauschinger effect, strain hardening, and the stress relaxation are examples of the hysteresis phenomena associated with the cyclic plasticity  [3,4,5,6]. The knowledge about the mechanical behavior of materials under the cyclic loading is essential for civil engineering in the prediction of their fatigue life  [7, 8]. The determination of material characteristics should not be based only on simple monotonic loading tests which might not include the fatigue of materials. Instead, the material response must be investigated in cyclic loading tests  [9, 10].

Most of elastoplastic materials exhibit cyclic hardening or softening under the proportional strain-controlled cyclic loading  [11,12,13,14]. Hardening defined as the increase of the yield stress in the wake of the plastic deformation shows that the yield function depends on: applied stress, the loading history, temperature, strain rate, and others  [14, 15]. Cyclic hardening and softening in various elastoplastic materials under strain-controlled cyclic loading have been widely investigated over the last few decades. Xu et al.  [16] examined the cyclic behavior of the yield point steel BLY160. The softening in stress and stiffness in the wake of the “flattening effect” of hysteresis loops was noted. The hardening of a 5052 aluminum alloy subjected to the cyclic compression–tension test was investigated in  [17]. The cyclic softening behavior of ultrafine grained Cu-Zn alloys was described in  [18]. In  [19] the cyclic hardening of PA6 aluminum in symmetrical strain-controlled cyclic tension–compression tests was presented. Materials which undergo the cyclic hardening involve increased stress in order to induce additional plastic deformation and exhibit higher cyclic yield strength than in monotonic loading tests  [20].

During the past thirty years, many constitutive models have been developed for describing inelastic responses of materials subjected to the cyclic loading  [21, 22]. Prager proposed the linear kinematic hardening model including the Bauschinger effect  [23, 24]. Frederick and Armstrong (F–A) modified the Prager’s model by adding one nonlinear relaxation term  [25, 26]. Based on the F–A kinematic hardening model, Chaboche proposed the decomposition of the nonlinear kinematic hardening into several kinematic rules used for the description of special ranges of strain  [27,28,29]. Due to the addition of several backstress components, the Chaboche model enables the better description of the material response to the external load when compared to F–A as well as the Prager model and is recommended in numerical simulations of complex cyclic phenomena, i.e., shakedown or ratcheting  [30, 31]. However, the increased number of backstresses makes the selection of hardening parameters more complicated and extends the computations time  [32].

The proper identification of hardening parameters is a very important issue under the scientific consideration  [33,34,35]. However, material hardening parameters obtained from numerical calculations can be found only with a certain precision. The improvement of the determination of hardening parameters might be achieved by various optimization methods  [36]. Nath et al.  [37] used the genetic algorithm in order to improve the simulation of ratcheting in the steel. In  [38] the multi-objective genetic algorithm with two fitness functions was applied for the parameters’ determination of the Chaboche kinematic hardening model. The computation of Chaboche hardening parameters by the Grey wolf optimization procedure is described in  [39].

The relatively new optimization method applied for cyclic loading tests is fuzzy logic. This non-deterministic computational method allows solving problems for which the knowledge about the considered model is incomplete. The application of the fuzzy set theory for the determination of Bodner–Partom model parameters is shown in  [40]. In this paper, for the first time the fuzzy logic was applied for the optimal selection of Chaboche parameters. The influence of the isotropic hardening is quite often neglected in numerical simulations of the strain-controlled cyclic loading, implying consideration of only the kinematic hardening component  [41]. Such approach does not ensure sufficient accuracy between experimental and numerical data, especially in modeling of more complex cyclic phenomena, e.g., shakedown or ratcheting. In this paper, the nonlinear Chaboche–Lemaitre (C–L) combined isotropic–kinematic hardening model was applied in numerical simulations of symmetrical strain-controlled cyclic tension–compression tests as well as the ratcheting phenomenon.

1.2 Objective and motivation

The far-reaching aim of this research is the analysis of severe plastic deformation (SPD) problems. In SPD problems the classical material processing methods are accelerated by the application of the additional cyclic load. This way, the tools forces and energy input can be reduced, the tools fatigue life can be extended, and material properties of the final product can be improved. A very good knowledge of the material properties and their variation due to the cyclic load is very important in the analysis of SPD problems. So far, commonly accepted methods for the calibration of hardening parameters can provide various sets of these parameters. The Chaboche–Lemaitre (C–L) combined isotropic–kinematic hardening model is considered in this paper. In order to choose the most reliable set of C–L hardening parameters, the fuzzy logic is used in this research for the first time. The hardening parameters are assumed to be fuzzy variables. This way, the scattering of hardening parameters is considered which confirms the results of experiments. An error of numerical approximation of the stress–strain curve registered in the symmetrical cyclic tension–compression test is the main measure of the solution convergence. This error constitutes the output fuzzy variable. The most reliable discrete (crisp) value of this error can be computed in the defuzzification step. The set of hardening parameters, for which the discrete error norm reaches the minimum, was assumed to be the optimum solution.

The advantage of the fuzzy logic analysis over the classical statistics is that the fuzzy sets theory considers not only the scattering of the input and output data, but also takes into consideration the influence of the mapping model. The set of elastic–plastic (mostly) differential equations was applied as the mapping model in this research. The material parameters calibration with the use of the fuzzy logic approach can be made even if only limited experimental results are available. This is very important when the experimental investigations are time-consuming or expensive. For a lot of data, the results of the fuzzy analysis are similar to the results of conventional statistics. Advantageous numerical processing of the experimental data can also help to reduce the number of experimental tests necessary to describe the elastic–plastic material response properly.

It is worth noting that the proposed approach, as general, can be applied not only in the identification of material parameters but also in analyses of complete sophisticated problems considered in terms of the fuzzy sets theory. It is especially important in the case of highly nonlinear and ill-conditioned problems  [42].

2 Theoretical framework

2.1 Constitutive equations

For a three-dimensional problem, the basic constitutive equations associated with both C–L combined isotropic–kinematic hardening are as follows. Here, we use the Voigt notation in which stress and strain tensors are represented as vectors.

  • The additive decomposition of the total strain increment into elastic and inelastic (plastic) components in a small-strain theory (Eq. 1):

    $$\begin{aligned} d\varvec{\varepsilon }=d\varvec{\varepsilon }^\mathrm{e}+{d\varvec{\varepsilon }}^\mathrm{p} \end{aligned}$$
    (1)

    where \(d\varvec{\varepsilon }\), \({d\varvec{\varepsilon }}^\mathrm{e}\) and \({d\varvec{\varepsilon }}^\mathrm{p}\) are the total, elastic, and plastic strain increments, respectively.

  • The Hook’s elasticity law in an incremental form (Eq. 2):

    $$\begin{aligned} d\varvec{\sigma }={\varvec{C}}d\varvec{\varepsilon }^\mathrm{e} \end{aligned}$$
    (2)

    where \(d\varvec{\sigma }\) is the stress increment and \(\varvec{C}\) is the constitutive matrix.

  • The yield surface based on the von Mises yield criterion (Eq. 3):

    $$\begin{aligned} f\left( \varvec{\sigma },\varvec{x},p \right) =\sqrt{\frac{3}{2}\left( \varvec{\sigma '}-\varvec{x} \right) \cdot \left( \varvec{\sigma '}-\varvec{x} \right) } -\sigma _{y}-r(p) \end{aligned}$$
    (3)

    where \(\varvec{\sigma '}\) is the deviatoric stress, \(\varvec{x}\) is a backstress defining the current center of the yield surface in the stress space, \(\sigma _{y}\) is the yield stress, r(p)is the isotropic hardening function describing the change of the yield surface, and dp is the effective plastic strain. The plastic flow occurs when \(f\left( \varvec{\sigma },\varvec{x},p \right) \ge 0\) otherwise; the response of the material is elastic.

  • The increment of an effective plastic strain dp (Eq. 4):

    $$\begin{aligned} dp=\sqrt{\frac{2}{3}{d\varvec{\varepsilon }}^\mathrm{p}\cdot {d\varvec{\varepsilon }}^\mathrm{p}}; \end{aligned}$$
    (4)

  • The normality condition (Eq. 5):

    $$\begin{aligned} {d\varvec{\varepsilon }}^\mathrm{p}=d\lambda \frac{\mathrm{d}f}{\mathrm{d}\varvec{\sigma }} \end{aligned}$$
    (5)

    where \(d\lambda \) is the plastic multiplier derived from the consistency condition, and \(\frac{\mathrm{d}f}{\mathrm{d}\varvec{\sigma }}=\varvec{n}\) as the normal to the yield surface determines the direction of the plastic strain increment.

  • For combined isotropic and kinematic hardening, the consistency condition is (Eq. (6))

    $$\begin{aligned} df\left( \varvec{\sigma },\varvec{x},p \right) = \frac{\partial f}{\partial \varvec{\sigma }}\cdot d\varvec{\sigma }+\frac{\partial f}{\partial \varvec{x}}\cdot d\varvec{x}+\frac{\partial f}{\partial p}dp=0. \end{aligned}$$
    (6)

    The equation for the backstress \(d\varvec{x}\) proposed by the Frederic–Armstrong model (Chaboche model with a single backstress) is given by (Eq. (7))  [43]:

    $$\begin{aligned} d\varvec{x}=\frac{2}{3}c{d\varvec{\varepsilon }}^\mathrm{p}-\gamma \varvec{x}dp \end{aligned}$$
    (7)

    where c is the kinematic hardening parameter representing the translation rate of the yield surface, and \(\gamma \) is the kinematic parameter determining the relaxation rate of the yield surface translation as the plastic deformation accumulates. Generally, c and \(\gamma \) are considered to be constant and \(c,\gamma >0\).

In C–L formulation the backstress consists of several \(x_{i}\) components \(i={1,2\ldots n }\) (Eq. (8))  [44]:

$$\begin{aligned} d\varvec{x}=\sum \limits _{i=1}^n {{d\varvec{x}}_{i} , }\qquad { d\varvec{x}}_{i}=\frac{2}{3}c_{i}{d\varvec{\varepsilon }}^\mathrm{p}-\gamma _{i}\varvec{x}_{i}dp. \end{aligned}$$
(8)

The evolution of isotropic hardening dr(p) is determined by the Voce isotropic law defined as (Eq. (9))  [45]:

$$\begin{aligned} dr\left( p \right) =b\left( Q-r \right) dp \end{aligned}$$
(9)

where Q is a saturated value of the isotropic hardening component, and b determines the rate in which the saturation is achieved.

2.2 Explicit and implicit integration of the constitutive equations

Equations (1)–(9) presented in Sect. 2 were applied in a numerical program simulating the elastic–plastic response at the point subjected to the external load. In the numerical procedure for the assumed strain increment, the plastic strain and stress increments are found. For each increment the following plastic state variables should be saved: backstresses, equivalent plastic strain, and the yield stress.

In most of the numerical computations presented in this research, the first-order forward Euler explicit integration algorithm was used. In explicit procedure the known solution for the time step \(t_{n}\) is extrapolated to the time \(t_{n+1}=t_{n}+\Delta t\). The main unknown is the plastic factor \(\lambda \) which for the flow rule associated with von Mises yield condition is equal to the equivalent plastic strain. The plastic multiplier is determined from the consistency condition enriched by the Kuhn–Tucker conditions (Eq. (10)):

$$\begin{aligned} \left\{ \begin{array}{l} \lambda \ge 0 \\ f\left( \varvec{\sigma },\varvec{x},p \right) \le 0 \\ \lambda f\left( \varvec{\sigma },\varvec{x},p \right) =0\\ \lambda df\left( \varvec{\sigma }, \varvec{x},p \right) =0 \\ \end{array}\right. \end{aligned}$$
(10)

The explicit integration presented in this paper is executed as follows:

  1. 1.

    For a given strain increment, the yield condition (3) is checked.

  2. 2.

    If \(f(\varvec{\sigma },\varvec{x},p)<0\), the material response is purely elastic and \(d\lambda =0, \lambda f\left( \varvec{\sigma }, \varvec{x},p \right) =0. \) The stress increment is calculated in line with Eq. (2).

  3. 3.

    If \(f(\varvec{\sigma },\varvec{x},p)\ge 0\), the material is in the yield state and \(d\lambda \) is computed using the following formula (Eq. (11)):

    $$\begin{aligned} d\lambda =\frac{\varvec{n}\cdot \varvec{C}d\varvec{\varepsilon }}{\varvec{n}\cdot \varvec{Cn}-\gamma \varvec{n}\cdot \varvec{x}+2/3c\varvec{n}\cdot \varvec{n+}{\partial f}/ {\partial p}}. \end{aligned}$$
    (11)
  4. 4.

    The plastic strain, the backstress, and the isotropic hardening increments at time t are calculated using Eq. (12):

    $$\begin{aligned} \left\{ {\begin{array}{l} {d\varvec{\varepsilon }}^\mathrm{p}=d\lambda \varvec{n} \\ d\varvec{x}_{i}=\frac{2}{3}c_{i}{d\varvec{\varepsilon }}^\mathrm{p}-\gamma _{i}(\varvec{x}_{i})dp \\ dr=b\left( Q-r \right) dp \\ \end{array}} \right. . \end{aligned}$$
    (12)
  5. 5.

    The stress increment \(d\varvec{\sigma }\) at time t is computed by the following formula (Eq. (13)):

    $$\begin{aligned} d\varvec{\sigma }=\varvec{C}(d\varvec{\varepsilon }-d\lambda \varvec{n}) \end{aligned}$$
    (13)

    where \(\varvec{n}\) is a normal vector at time t.

  6. 6.

    Finally, stress, plastic strain, isotropic hardening variable, and the backstress are updated for the \(t_{n+1}\) step time (Eq. (14)):

    $$\begin{aligned} \left\{ \begin{array}{*{20}c} \varvec{\sigma }_{t+\Delta t}=\varvec{\sigma }_{t}+d\varvec{\sigma }\\ \varvec{\varepsilon }^\mathrm{p}_{t+\Delta t}=\varvec{\varepsilon }^\mathrm{p}_{t}+{d\varvec{\varepsilon }}^\mathrm{p}\\ r_{t+\Delta t}=r_{t}+dr\\ {\varvec{x}_{t+\Delta t}=\varvec{x}_{t}+d\varvec{x}}.\\ \end{array} \right. \end{aligned}$$
    (14)

It can be shown that for the explicit integration algorithm for C–L combined nonlinear isotropic–kinematic hardening model in 1D case the stress increment is (Eq. (15)):

$$\begin{aligned} d\sigma =E\left( 1-\frac{E}{E+\sum _i \left( c_{i}-\mathrm{sign}\left( d\varepsilon \right) \gamma _{i}\cdot x_{i} \right) +b\left( Q-r \right) }\right) d\varepsilon . \end{aligned}$$
(15)

The main advantage of the use of the explicit integration is its simplicity  [46]; however, this method is conditionally stable and accurate only for a small time/load increment \(\Delta t\)  [47]. Here, we used four thousand strain increments for a single hysteresis loop, although acceptable results can be obtained for only four hundred strain increments.

The explicit integration is suitable if up to several hundred hysteresis loops are computed. The fuzzy logic analysis presented in this paper requires generating several hundred thousand hysteresis loops. An explicit integration is not computationally effective, and an implicit predictor–corrector procedure is applied, therefore. The implicit integration is unconditionally stable, and less time/load increments are necessary as compared to the explicit procedure. For simplicity the predictor–corrector integration procedure was derived here for only 1D case.

For a given strain increment \(\mathrm {\Delta }\varepsilon \), the trial stress is (Eq. (16)):

$$\begin{aligned} \sigma ^{tr}=\sigma +E\mathrm {\Delta }\varepsilon . \end{aligned}$$
(16)

If the trial stress is beyond the yield surface, the plastic corrector is needed (Eq. (17)):

$$\begin{aligned} \sigma ^\mathrm{corr}=-E\mathrm {\Delta }\varepsilon ^\mathrm{p}. \end{aligned}$$
(17)

Assuming that the actual stress should be related to the backstress, the yield function (see Eq. (3)) is (Eq. (18)):

$$\begin{aligned} f=\left| \sigma ^{tr}-\sigma ^\mathrm{corr}-x \right| -\sigma _{y}-r=0. \end{aligned}$$
(18)

The integration of Eq. 9 gives (Eq. (19)):

$$\begin{aligned} r\left( \varepsilon ^\mathrm{p} \right) =Q\left( 1-e^{-b(\varepsilon ^\mathrm{p}+\mathrm {\Delta }\varepsilon ^\mathrm{p})} \right) , \end{aligned}$$
(19)

and the integration of Eq. (7). with nonzero boundary conditions \({x=x}_{0}\) and \(\varepsilon ^\mathrm{p}=\varepsilon _{0}\) provides (Eq. (20)):

$$\begin{aligned} x=\frac{c}{\gamma }-\left( \frac{c}{\gamma }-x_{0} \right) e^{-\gamma \left( \varepsilon ^\mathrm{p}+\mathrm {\Delta }\varepsilon ^\mathrm{p}-\varepsilon _{0} \right) }. \end{aligned}$$
(20)

After inserting Eqs. (16), (17), (19), (20) into Eq. (18), the nonlinear equation with unknown plastic strain increment \(\mathrm {\Delta }\varepsilon ^\mathrm{p}\) is obtained. This equation can be solved numerically using, e.g., Newton’s method. The rest of the procedure is the same as in the explicit one (Eqs. (12)–(14)). Special attention should be given to signs in Eq. (20) when the load reverses.

The extension of the predictor–corrector procedure to the 3D case is straightforward. In 3D case the plastic corrector is (Eq. (21)):

$$\begin{aligned} \varvec{\sigma }^\mathrm{corr}=-3G{\Delta }\varvec{\varepsilon }^\mathrm{p} \end{aligned}$$
(21)

where G is the shearing modulus.

For a single hysteresis loop, we used only forty strain increments in the implicit integration procedure. Both integration schemes: explicit (four thousand increments in a single hysteresis loop) and implicit (forty increments) provide an excellent convergence.

3 Experimental investigation and preliminary calibration of the hardening parameters

3.1 Experimental research and the determination of the hardening parameters

The symmetrical strain-controlled cyclic tension–compression test was carried out to identify the hardening parameters as well as to assess the cyclic behavior of a PA6 aluminum alloy. The physical, chemical, and mechanical properties of tested PA6 aluminum are listed in Table 1.

Table 1 Properties of a PA6 aluminum used in experimental tests
Full size table

The experiment was carried out under strain-controlled conditions, at an ambient temperature (Fig. 1). The deformation \(\Delta \varepsilon =\pm \)2% of the 50 mm measuring base repeated for seven cycles was applied in this research. The elongation of the specimen was measured using the extensometer (ZWICK ROELL, Germany) mounted on the measuring base.

The experimental force–elongation data are converted first into engineering stress–strain relation (\(\sigma _{eng}, \varepsilon )\) and later on into true stress–strain (\(\sigma ,\varphi )\) data using Eqs. (22) and (23),

$$\begin{aligned} \sigma= & {} \sigma _\mathrm{eng}(1+\varepsilon ), \end{aligned}$$
(22)
$$\begin{aligned} \varphi= & {} \ln (1+\varepsilon ). \end{aligned}$$
(23)
Fig. 1
figure 1

The sample subjected to the cyclic tension–compression test

Full size image

In order to analyze the cyclic behavior of a PA6 aluminum using the F–A and C–L isotropic–kinematic hardening model, a set of four (F–A model) to eight parameters (C–L model with three backstresses) has to be determined. The proposed methodology to select the initial values of the hardening parameters is described in the following.

Parameters Q and b were estimated from the initial and stabilized hysteresis loops obtained from the experimental stress–strain curve registered in the symmetrical strain-controlled cyclic tension–compression test. The Q parameter was indicated as the increase in the yield stress between the initial yield stress (\(\sigma _{y0})\) and the saturated one \(\sigma _{y}\) recorded in the final stabilized loop (Eq. 24):

$$\begin{aligned} Q=\sigma _{y}-\sigma _{y0}. \end{aligned}$$
(24)

The parameter b determines the rate of the yield stress increase depending on the number of cycles up to the saturation. For low values of b, the material stabilizes relatively slow, while high values of b stabilize the isotropic hardening rapidly  [17, 48]. It was noted that the isotropic hardening for PA6 aluminum stabilizes in a few cycles. The initial values of Q and b isotropic parameters were initially considered as 150 MPa and 18, respectively.

Kinematic hardening parameters \(c_{i}\) and \(\gamma _{i}\) (\(i=1,2,3\)) were selected using two approaches based on the half-cycle or based on the stabilized hysteresis loop stress–strain data. The first method is suitable for limited experimental data when only few cycles of loading are available  [49]. The second method is recommended in the analysis of the long-term cyclic analyses.

In order to get the calibration stress–plastic strain curve, the yield stress was determined using the 0.2% offset method. At this point, the plastic strain equals zero. For each data pair of the calibration curve (\(\sigma _{k},\varepsilon ^\mathrm{p}_{k})\), the value of \(x_{k}\) is calculated as shown in Eq. (25), where \(\sigma _{i}\) is the size of the yield surface at the corresponding plastic strain for the isotropic hardening component of the yield stress (found for already computed Q and b parameters),

$$\begin{aligned} x_{k}=\sigma _{k}-\sigma _{i}. \end{aligned}$$
(25)

Next, the backstress evolution law (Eq. (26)) is used for the estimation of \(c_{i}\) and \(\gamma _{i}\) parameters,

$$\begin{aligned} x_{i}=\frac{c_{i}}{\gamma _{i}}(1-e^{-\gamma _{i}\varepsilon ^\mathrm{p}}). \end{aligned}$$
(26)

Here, for the calibration of \(c_{i}\) and \(\gamma _{i}\) parameters, the nonlinear numerical procedure implemented in commercial Simulia Abaqus software was used.

In the second tested approach, parameters \(c_{i}\) and \(\gamma _{i}\) were determined from the last stabilized cycle (Fig. 2) where the saturation of the isotropic hardening component takes place (the influence of isotropic hardening is neglected in the analysis)  [50]. The plastic strain was calculated using the additive decomposition of generalized strain assuming that each pair of data (\(\sigma _{k},\varepsilon ^\mathrm{p}_{k}\)) should be specified with the strain shifted to \(\varepsilon ^\mathrm{p}_{0}\) (Eq. (27))  [49]:

$$\begin{aligned} \varepsilon ^\mathrm{p}_{k}=\varepsilon _{k}-\frac{\sigma _{k}}{E}-\varepsilon ^\mathrm{p}_{0} \end{aligned}$$
(27)

where \(\varepsilon ^\mathrm{p}_{0}\) determines the translation of the yield surface (Fig. 2).

The value of \(x_{k}\) for each (\(\sigma _{k},\varepsilon ^\mathrm{p}_{k}\)) data pair might be calculated by the use of Eq. (28):

$$\begin{aligned} x_{k}=\sigma _{k}-\sigma ^{s} \end{aligned}$$
(28)

where \(\sigma ^{s}\) defines the stabilized size of the yield surface and might be calculated using Eq. (29):

$$\begin{aligned} \sigma ^{s}=\frac{\sigma _{1}+\sigma _{n}}{2}. \end{aligned}$$
(29)

In the calibration of \(c_{i}\) and \(\gamma _{i}\) Chaboche kinematic hardening parameters, the procedure implemented in Abaqus program was used once again.

Fig. 2
figure 2

The stress–strain curve for the stabilized hysteresis loop

Full size image

According to Chaboche  [50], three hardening rules are recommended in simulations of a stable hysteresis loop (Fig. 3). The first rule \((x_{1})\) should start hardening with a very large modulus and stabilize quickly. The second rule \((x_{2})\) should simulate the transient nonlinear portion of the stable hysteresis curve. The third rule \((x_{3})\) should be almost linear \((\gamma _{3}\rightarrow 0)\) to represent the subsequent linear part of a hysteresis curve at large strains  [51]. According to Bari and Hassan  [52], the introduction of small nonlinearity \((0{<\gamma }_{3}<9)\) improves the quality of the ratcheting simulations.

Fig. 3
figure 3

Kinematic hardening model with three backstresses

Full size image

The experimental true stress–strain curve resulting from experimental data is shown in Fig. 4. It was noted that the material tends to stabilize after seven cycles. In the identification of kinematic and isotropic parameters, the data from the first loop and alternative from the last stabilized cycle were used.

Fig. 4
figure 4

The experimental true stress–true strain curve for PA6 aluminum

Full size image

The kinematic hardening parameters for F–A and C–L hardening models computed by the half-cycle approach are given in Table 2. Numerically generated curves for such computed hardening parameters are shown in Fig. 5.

Table 2 Values of hardening parameters for the half-cycle procedure
Full size table
Fig. 5
figure 5

The comparison of experimental and numerical stress–strain curves for F–A and Voce models (a) and for the C–L isotropic–kinematic hardening model with two (b) and three (c) backstresses (half-cycle procedure)

Full size image

One can see an acceptable convergence of experimental and numerical hysteresis loops for the Frederick–Armstrong model, clear qualitative improvement of the convergence in two backstresses for the Chaboche–Lemaitre model, and only slight improvement in the three backstresses model. However, when considering ill-conditioned problems, e.g., ratcheting phenomenon, the influence of the third backstress on the solutions precision is very important.

The material kinematic hardening parameters computed in the procedure based on stabilized cycle data are listed in Table 3. The comparison of experimental and numerical curves obtained for the stabilized cycle approach is presented in Fig. 6. The differences between parameter values are associated with that the best fit is achieved for the first hysteresis loop in the half-cycle procedure and for the last loop in the stabilized hysteresis loop approach.

Table 3 Values of hardening parameters for the stabilized cycle procedure
Full size table
Fig. 6
figure 6

The comparison of experimental and numerical stress–strain curves for F–A model (a) and for the C–L isotropic–kinematic hardening model with two (b) and three (c) backstresses (stabilized cycle procedure)

Full size image

A very good fitting between experimental and numerical curves for initially calibrated hardening parameters was obtained for all tested models. However, the application of C–L model with two and three relaxation terms has improved significantly the convergence between numerical and experimental curves. Among considered C–L models, a slightly better compatibility was achieved for one with three backstresses in both tested procedures. The C–L model with three kinematic rules will be applied in other tests, therefore.

3.2 Enhancement of the hardening parameters using the least-square method

The comparison of the hysteresis loops registered in experimental tests to the numerical ones enables to calibrate the hardening parameters. In order to achieve better convergence, the optimization procedure based on the least-square method is applied next. The aim of this method is the minimization of the square of the difference between the measured stress values (\(\sigma _\mathrm{exp})\) and their numerically approximated values (\(\sigma _\mathrm{appr})\)  [53]. The error norm \(\left\| B \right\| \) is defined as (Eq. (30)):

$$\begin{aligned} \left\| B \right\| = \sqrt{\int _{0}^{\varepsilon {\max }} {{(\sigma _\mathrm{exp}-\sigma _\mathrm{appr}(c_{i},\gamma _{i},b,Q))}^{2}d\varepsilon }} \end{aligned}$$
(30)

where \(\varepsilon _{\max }\) is the maximum strain reached in the experiment.

Table 4 Values of hardening parameters for the C–L combined isotropic–kinematic hardening model with three backstresses
Full size table
Fig. 7
figure 7

The comparison of experimental and numerical stress–strain curves after the optimization procedure; C–L model with three backstresses—the half-cycle procedure (a), and C–L model—the stabilized hysteresis loop approach (b)

Full size image
Fig. 8
figure 8

Backstress and isotropic hardening versus time; C–L model with three backstresses—the half-cycle procedure (a), and the C–L model—the stabilized hysteresis loop approach (b)

Full size image

In the optimization procedure, the initially determined hardening parameters for the C–L isotropic–kinematic hardening model were randomly distorted up to 20%, and for each set the error norm (30) was computed. The hardening parameters minimizing the error norm \(\left\| B \right\| \) are presented in Table 4. Numerically generated stress–strain curves related to experimental ones are shown in Fig. 7. The plots of backstress and isotropic hardening versus time are presented in Fig. 8.

Table 5 Comparison of experimental and numerical curves for different sets of hardening parameters appointed by the least-square method with similar error norm values
Full size table

It can be seen in Fig. 7 that very good agreement between experimental and numerical curves was reached in all the cases. The application of the optimization procedure has improved the convergence in all considered cases.

4 The application of the fuzzy set theory in the determination of the hardening parameters and the selection of the most reliable data

4.1 Fuzzy logic analysis

In engineering problems the information about a considered phenomenon is quite often incomplete or insufficient. Soft computing methods, among which the fuzzy set theory is the most popular, include the presence of uncertainty of both the data and the mathematical model. Fuzzy logic enables to find the most reliable solution of the considered problem  [40].

The fuzzy set theory might be an effective tool in the determination of hardening parameters. Although the optimization procedure based on the least-square method mentioned in the previous Section enhances the convergence between experimental and numerical curves, a similar small error can be observed for various sets of hardening parameters (Table 5). The very important question arises here which set of parameters describes the model behavior in the best way. The fuzzy logic can help to select the optimal set of material hardening parameters.

The fuzzy set theory is a type of statistics which can be done even if only limited number of experimental data is available. The main advantage of the fuzzy set theory over the distance norm (30) is that the fuzzy approach considers the uncertainty of the input (experimental) data. Fuzzy analysis also takes into consideration the influence of the mapping model (unlike the classical statistics) on the output variable(s). In this research, the input fuzzy variables are material hardening parameters, while the fuzzy output variable is the error norm (30).

Another very important advantage of the fuzzy logic is that the most reliable result (crisp value) can be selected in the fuzzy solution. Our experience gained in the previous research is that the crisp value is practically independent of the form of the membership function (triangle, trapezoid, Gauss-like shape). Thus, it is an objective the most representative value of the fuzzy output variable. It is also worth noting that fuzzy logic can also easily take into consideration so-called linguistic variables, e.g., hard–soft, smooth–rough, hot–cold, high quality–poor quality, etc. (In this research, linguistic variables are not considered.) These sense-based descriptions are hard to implement in other numerical methods.

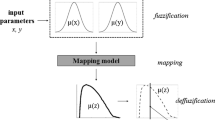
The aim of fuzzy analysis is the conversion of fuzzy input parameters into the result space using the mapping model (Fig. 9). The input variables must be first fuzzed, i.e., their membership functions should be defined. The fuzzification step provides the information about the scattering of input parameters and the acceptance of their dispersion. Here, material hardening parameters are the fuzzy input variables. The most simple triangle membership functions associated with hardening parameters are chosen for the fuzzy analysis. The ranges of the hardening parameters have been selected during the execution of the optimization procedure. The limiting values of material hardening parameters are collected from solutions providing the best fitting of numerical and experimental data.

Fig. 9
figure 9

The mapping of two sets of fuzzy input variables into the results space

Full size image

In the approximation error (30) fuzzified by the associated membership function, the crisp value can be found. This discrete value corresponds to the most reliable solution—the most expected approximation error for material hardening parameters defined with some uncertainty.

Readers not familiar with the fuzzy logic analysis can find more details in  [40, 54, 55]. Reference  [55] contains many interesting examples of the fuzzy logic applications in the analysis of structural elements and engineering structures.

From a variety of methods used in the fuzzy analysis in this research, the \(\upalpha \)-level optimization approach was applied. The principle of this method is described in the following. The membership functions associated with the fuzzy input variables are separated into the sufficient number of \(\upalpha \)-levels. For a specific \(\upalpha \)-level, the boundary \(c_{i \alpha kl},c_{i \alpha kr},\gamma _{i \alpha kl}, \gamma _{i \alpha kr}, \quad b_{\alpha kl}, b_{\alpha kr},Q_{\alpha kl}, Q_{\alpha kr}\) values are searched. For certain \( Q,b,c_{i}, \gamma _{i}\) input parameters, the minimum \(B_{\alpha kl}\) and maximum \(B_{\alpha kr}\) values are computed which define the shape of the fuzzy output membership function. The procedure is repeated for all considered \(\upalpha \)-levels. The searching of extreme B values is formulated as the optimization problem described as follows (Eq. 31):

$$\begin{aligned} \left\{ {\begin{array}{l} B=f(Q,b,c_{i}, \gamma _{i})\Rightarrow \mathrm {min}(Q,b,c_{i}, \gamma _{i})\in X_{\alpha k} \\ B=f(Q,b,c_{i}, \gamma _{i})\Rightarrow \mathrm {max}(Q,b,c_{i}, \gamma _{i})\in X_{\alpha k} \\ \end{array}} \right. \end{aligned}$$
(31)

where requirements \((Q,b,c_{i}, \gamma _{i})\in X_{\alpha k}\) define constraints of the optimization procedure.

The continuity of the mapping operator as well as the convexity of a fuzzy result space (Eq. 32) are constraints of the \(\alpha \)-level optimization  [55]. This method ensures smooth results with a smaller number of calculations in comparison to the more general extension principle approach described in  [40, 54, 55] and is recommended in structural analyses,

$$\begin{aligned} \left\{ \begin{array}{l} \mu \left( c_{i 2} \right) \ge \min \left[ \mu \left( c_{i 1} \right) , \mu \left( c_{i 3} \right) \right] \forall c_{i 1}, c_{i 2}, c_{i 3}\in X \cap c_{i 1}\le c_{i 2}\le c_{i 3} \\ \mu \left( \gamma _{i 2} \right) \ge \min \left[ \mu \left( \gamma _{i 1} \right) , \mu \left( \gamma _{i 3} \right) \right] \forall \gamma _{i 1}, \gamma _{i 2}, \gamma _{i 3}\in X \cap \gamma _{i 1}\le \gamma _{i 2}\le \gamma _{i 3} \\ \mu \left( Q_{2} \right) \ge \min \left[ \mu \left( Q_{1} \right) , \mu \left( Q_{3} \right) \right] \forall { Q}_{1}, Q_{2}, Q_{3}\in X \cap Q_{1}\le Q_{2}\le Q_{3}\\ \mu \left( b_{2} \right) \ge \min \left[ \mu \left( b_{1} \right) , \mu \left( b_{3} \right) \right] \forall { b}_{1}, b_{2}, b_{3}\in X \cap b_{1}\le b_{2}\le b_{3}. \\ \end{array} \right. \end{aligned}$$
(32)

The transformation of fuzzy results into the output crisp value is made using a decision-making algorithm based on different defuzzification methods, e.g., the rank level method, the mean of maximum, etc.  [55, 56]. The mass center method is used here in searching for the most reliable discrete values of the hardening parameters. The mass center of the output membership function \(\mu \left( B \right) \) associated with the fuzzy approximation error B (Eq. (30)) can be computed from (Eq. (33))  [55]:

$$\begin{aligned} B_{0}=\frac{\int {B\cdot \mu (B)\mathrm{d}B} }{\int {\mu (B)\mathrm{d}B} } \end{aligned}$$
(33)

where \(B_{0}\) is a crisp value of the B output variable, and \(\mu (B)\) is the membership function of the B variable.

Table 6 Hardening parameter values computed by the fuzzy logic for the C–L combined isotropic–kinematic hardening model with three backstresses
Full size table
Fig. 10
figure 10

The comparison of experimental and numerical stress–strain curves after the fuzzy logic analysis: half-cycle procedure (a), stabilized hysteresis loop approach (b)

Full size image
Fig. 11
figure 11

Backstress and isotropic hardening versus time; C–L model with three backstresses—the half-cycle procedure (a), and the C–L model—the stabilized hysteresis loop approach (b)

Full size image

The fuzzy logic-based algorithm for the calibration of hardening parameters applied in this research is as follows:

  1. 1.

    The initially determined isotropic and kinematic hardening parameters are treated as fuzzy input variables. In the fuzzification step, the variation of hardening parameters was based on the optimization procedure (the limiting values of material hardening parameters are collected from solutions providing the best fitting of numerical and experimental data). Triangular membership functions associated with hardening parameters were constructed.

  2. 2.

    Fuzzy analysis was performed using the \(\upalpha \)-level optimization method. The fuzzy output variable B and its membership function \(\mu \left( B \right) \) were calculated.

  3. 3.

    The most reliable discrete value \(B_{0}\) was found in the defuzzification step.

  4. 4.

    The procedure was repeated for randomly distorted hardening parameters. The set of distorted hardening parameters, for which the discrete approximation error \(B_{0}\) was minimal, provides the most reliable calibration.

To sum up, in the proposed fuzzy logic approach for the determination of hardening parameters, the most reliable calibration provides a very good convergence of numerical as well as experimental hysteresis curves, and small variations of these parameters will have a minimal impact on this convergence.

4.2 Results of the fuzzy logic analysis

The hardening parameters for the C–L combined isotropic–kinematic hardening model computed by the fuzzy logic are listed in Table 6. The comparison of the results obtained in the experimental investigations and results of numerical analysis including hardening parameters obtained in the fuzzy logic computations is presented in Fig. 10. A very good agreement between experimental and numerically generated stress–strain curves was achieved for both half-cycle and stabilized hysteresis loop procedures. The numerically generated plots of backstress and isotropic hardening versus time are shown in Fig. 11.

4.3 Supplementary experimental test

Although advanced fuzzy logic-based processing of experimental data can help to reduce the number of necessary experimental tests, a few experimental investigations are recommended in order to improve the quality of determined material data. For this reason, another strain-controlled cyclic tension–compression test for \(\Delta \varepsilon =\pm 4\)% was done. Unfortunately, this test was terminated in the fourth cycle as the result of the sample brittle fracture. Moreover, slight buckling of the sample was observed in the compression load. Thus, for considered PA6 aluminum the range of deformation \(\Delta \varepsilon =\pm 4\)% seems to be the limiting case. Despite technical problems, the stress–strain curve registered in experimental investigations looks accurate. The comparison of hysteresis loops for \(\Delta \varepsilon =\pm 2\)% and \(\Delta \varepsilon =\pm 4\)% is shown in Fig. 12.

Fig. 12
figure 12

Comparison of stress–strain curves registered in \(\Delta \varepsilon =\pm 2\)% and \(\Delta \varepsilon =\pm 4\)% experiments

Full size image

There is an open question how to process the data collected in several tests. The following approaches are available:

  • the analysis presented in previous Sections can be repeated for each tests, and the mean values of hardening parameters can be found,

  • the error norm (30) can be extended over all experimental tests, and a cumulative analysis can be made,

  • the error norm (30) can be enhanced by weighting factors depending on the measurements precision (test \(\Delta \varepsilon =\pm 4\)% is less reliable due to the technical problem that occurred)

  • other types of tests can be made, e.g., cyclic elastic–plastic torsions of the thick-walled cylinder,

  • non-symmetrical tests can be done as well as the influence of temperature and various strain rates can be considered in order to analyze visco-plastic effects, etc.

The appropriate approach depends on the researcher’s needs. The discussion about possible solutions is out of the scope of this paper. In this paper, the authors decided to make investigations focusing on answers to the following two questions:

  • Can hardening parameters determined in the \(\Delta \varepsilon =\pm 2\) test provide a reasonable approximation of the \(\Delta \varepsilon =\pm 4\)% test?

  • What is the distortion of hardening parameters computed separately from \(\Delta \varepsilon =\pm 2\)% and \(\Delta \varepsilon =\pm 4\)% tests?

The positive answer for the first question confirms the assumption that the fuzzy logic-based approach can help to reduce the number of experimental investigations necessary to determine the material hardening parameters. The numerical approximation of hysteresis loops registered in \(\Delta \varepsilon =\pm 4\)% test based on the hardening parameters determined in the \(\Delta \varepsilon =\pm 2\)% test is presented in Fig. 13. (The hardening parameters determined in \(\Delta \varepsilon =\pm 2\)% test are placed in the column titled “stabilized hysteresis loop” in Table 6.) Very good convergence between experimental and numerical hysteresis plot was obtained—this convergence is even better than it was expected.

Fig. 13
figure 13

Numerical approximation of a \(\Delta \varepsilon =\pm 4\)% test

Full size image

With Regard to the second question, the whole analysis was repeated for measurements registered in the \(\Delta \varepsilon =\pm 4\)% test. The values of the obtained material hardening parameters are given in the Table 7.

Table 7 Hardening parameters computed by the fuzzy logic for C–L model with three backstresses for the \(\Delta \varepsilon =\pm 4\)% test (results from the \(\Delta \varepsilon =\pm 2\)% test are placed in brackets)
Full size table

The comparison of hardening parameters presented in Table 7 shows an acceptable convergence between the fuzzy logic results for \(\Delta \varepsilon =\pm 2\)% and \(\Delta \varepsilon =\pm 4\)% tests analyzed separately. The dispersion of hardening parameters is much smaller than for those presented in Table 5.

A good knowledge of material hardening parameters extends the information about the elastic–plastic material response. The numerically generated plots of strain, stress, backstress, and isotropic hardening versus time are shown in Fig. 14. One can clearly see the nonlinear isotropic and kinematic hardening, the zones of elastic and plastic responses, as well as the saturation of the isotropic hardening.

Fig. 14
figure 14

Strain (a), stress (b), backstress (c), and isotropic hardening (d) versus time

Full size image

5 Validation of the determined the hardening parameters in a ratcheting test

In this Section, the C–L combined isotropic–kinematic hardening model is used to simulate the cyclic behavior of the ratcheting phenomenon. Ratcheting is a rate-independent elastoplastic phenomenon which occurs under the non-symmetrical loading of materials with a constant nonzero mean stress causing plastic strain increase cycle by cycle  [57,58,59,60]. If the deformation is unconstrained for a high enough mean stress, the ratchet plastic strain can lead to failure of the structure. The material response for non-symmetrical cyclic loading is very sensitive to materials hardening parameters. In the combined nonlinear isotropic/kinematic hardening, the center of the yield surface moves in the stress space due to the kinematic hardening component, and the range of the yield surface expands due to the isotropic component  [61]. It was noted that the kinematic hardening does not change the plastic strain increase in subsequent cycles of loading  [62]. The isotropic hardening component results in the gradual deceleration, quasi-shakedown or even blocking of the ratcheting phenomenon  [63].

The stress-controlled cyclic loading test has been made to validate material hardening parameters given in Table 6 in the right-hand-side column. The sample has been subjected to non-symmetrical tension–compression load. The assumed load history is presented in Fig. 15. It was selected to cause yielding for both tension and compression load in all load cycles. This test was later on numerically simulated.

Fig. 15
figure 15

The load history applied in a non-symmetrical cyclic tension–compression test

Full size image

The comparison of the results of numerical and real experiments is presented in Fig. 16. It can be seen that the experimental data are in a good agreement with numerical results which proves the correct identification of materials hardening parameters. It is worth noting that in the ratcheting test the C–L model with three backstresses is recommended.

Fig. 16
figure 16

The comparison of true stress–true strain relations obtained in experimental and numerical ratcheting tests

Full size image

Although in experiment (due to the restrictions of the testing machine) only four load cycles are registered, in the numerical test several dozen load cycles can be applied in order to observe the stabilization of the hysteresis loops caused by the isotropic hardening (Fig. 17).

Fig. 17
figure 17

Stabilization of the ratcheting test—numerical simulation

Full size image

6 Validation of the determined hardening parameters in a cyclic mean stress relaxation test

Following the stress-controlled test presented in the previous Section, the strain-controlled test is proposed here. For the maximum and minimum strains fixed (both introduce plastic deformations), the stress relaxation occurs. Due to the application of cycling loading, the progressive relaxation of initially nonzero mean stress to a saturated near-zero value will take place  [64, 65]. For constant strain amplitude, the plastic deformation would also result in the vertical shift of the stress–strain curves towards the zero-mean stress position. This shift in the vertical direction is associated with the mean-stress shift and is equivalent to the reduction of the residual stress  [66]. Both ratcheting and mean stress relaxation phenomenon are characterized by unclosed hysteresis loops. The plastic shakedown occurs after a certain number of cycles.

For the validation of the proposed Chaboche nonlinear isotropic–kinematic hardening model, the mean stress relaxation test during the asymmetrical strain cycling with constant nonzero mean strain was carried out and compared with its numerical simulations. This test in conjunction with the ratcheting could be useful for the determination of the hardening parameters.

In the mean stress relaxation test presented here, the initial deformation of the specimen \(\varepsilon _{\mathrm {init}}=1.5{\%}\) is applied. After that, the test was continued from this state with the strain variation \(\Delta \varepsilon =\pm 0.8{\%}\).

Fig. 18
figure 18

Comparison of experimental and numerical true stress–true strain curves obtained in the mean stress relaxation test

Full size image

The results of the mean stress relaxation test and its numerical verification are shown in Fig. 18. It can be seen that hysteresis loops shift downwards due to the cycling loading and tend to stabilize after a certain number of cycles. Although each hysteresis loop shifts descents, the amount of this shift varies at different strain points. One can notice the increase of the yield locus after several load cycles. It is caused by the isotropic hardening which dominates over the kinematic one. In fact, the saturated stress in the isotropic hardening is \(Q=131.4\) MPa, while the saturated back stress is \(\Sigma {c}_{{i}}/\gamma _{{i}}=96.7\, \hbox {MPa}\).

It can also be observed in Fig. 18 the good convergence between the experimental data and computational results. The Chaboche nonlinear isotropic–kinematic hardening model used in this simulation describes accurately the mean stress relaxation behavior.

Fig. 19
figure 19

Relaxation of the mean stress (experimental and numerical results) versus loading cycles

Full size image

The mean stress relaxation occurring due to the cyclic loading is shown in Fig. 19. It can be seen that the mean stress decreases with each cycle and stabilizes to a near-zero certain value. The decrease of the mean stress value is rapid during early cycles of loading, then the mean stress relaxation has nearly constant rate. Relatively good agreement between the simulation results and the experimental data of the mean stress relaxation was obtained. It shows that the proposed Chaboche nonlinear isotropic–kinematic hardening model can accurately describe the evolution of the mean stress relaxation.

7 Conclusions

The identification of material hardening parameters plays an important role both in experimental tests and in numerical simulations. The knowledge of hardening parameters is especially important in the analysis of problems with symmetric and non-symmetric cyclic loads. Unfortunately, for multi-parameter models (e.g., Chaboche–Lemaitre model with three backstresses) the calibration of the hardening parameters is not an unambiguous process. Quite good fitting of numerical simulations to the results of experiments can be reached for various sets of hardening parameters. In this paper, two approaches for hardening parameters calibrations: half-cycle procedure and stabilized hysteresis loop procedure are investigated. The application of the optimization procedure based on least-square method minimizing an approximation error was used for the enhancement of the convergence between experimental and numerical data. For the selection of the most reliable solution, an original procedure based on the fuzzy logic theory was used in this paper. Based on the analyzed results, the main conclusions are as follows:

  1. 1.

    The application of the half-cycle and the stabilized cycle procedures provide different sets of the hardening parameters, although very good convergence to the experimental data is achieved in both cases.

  2. 2.

    The use of the optimization procedure based on the least-square method has improved the convergence between experimental and numerical hysteresis loops.

  3. 3.

    The fuzzy analysis enables to select the most reliable set of hardening parameters including the scattering of both input and output data and investigates the influence of the mapping model on the final results.

  4. 4.

    Although in some sense the results of the fuzzy analysis are similar to the results of pure statistics, fuzzy logic does not require a lot of experimental data. In limit, the fuzzy analysis can be performed even if only a single measurement is available unless this measurement is enriched by the expert’s knowledge.

  5. 5.

    The good agreement between experimental and numerical results is obtained in the ratcheting and relaxation tests which prove the correct identification of material’s hardening parameters. It is worth noting that ratcheting and relaxation tests can be used in the determination of hardening parameters as supported tests or as the basic tests depending of the researcher’s needs and goals.

  6. 6.

    The comparison of hardening parameters determined separately in \(\Delta \varepsilon =\pm 2\)% and \(\Delta \varepsilon =\pm 4\)% tests shows a suitable convergence. It is not always possible to investigate the whole envelope of strains existing in the structure in service, and therefore, the extrapolation of strains reached in an experiment is possible. Such an example is the extrusion process in which strains up to even 300% or more occur.

  7. 7.

    The approximation of stress–strain curves registered in \(\Delta \varepsilon =\pm 4\)% test based on hardening parameters obtained in \(\Delta \varepsilon =\pm 2\)% test is very good. Thus, advanced numerical processing of experimental data can help to reduce the number of experimental tests necessary to determine material hardening parameters.

The numerical simulations presented here show the potential of the application of fuzzy logic for the determination of hardening parameters. The proposed fuzzy logic approach is general and can be extended to other more sophisticated models.