Skip to main content
SpringerLink
Log in

Dynamic response of an irregular heterogeneous anisotropic poroelastic composite structure due to normal moving load

  • Original Paper
  • Published:
Acta Mechanica Aims and scope Submit manuscript

Abstract

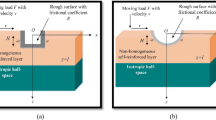
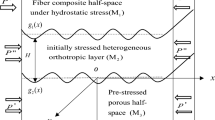
The present study is concerned with the dynamic response of an anisotropic composite structure due to a normal moving load on its irregular rough surface. The composite structure is comprised of an irregular incompressible heterogeneous transversely isotropic fluid-saturated poroelastic layer lying over a transversely isotropic substrate. The mathematical formulation of this structure gives rise to a boundary value problem with specified boundary conditions, and the perturbation method has been used to tackle the irregular surface problem. The expressions for the induced shear and normal stresses in layer and substrate of the composite structure are derived analytically in closed form due to the moving load. As a special case of the problem, the deduced expressions of the induced stresses are validated with the pre-established and standard results. The effect of several substantial parameters such as vertical depth, heterogeneity parameter, porosity parameter, frictional coefficient, irregularity depth, and irregularity factor on the induced shear as well as normal stresses of the layer and substrate has been delineated graphically by the numerical computation. Moreover, a comparative study of the various types of irregularity, namely rectangular irregularity, parabolic irregularity and no irregularity (regular boundary surface) on the induced shear and normal stresses in the layer and, substrate, is carried out by means of graphs, and some considerable peculiarities are outlined.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6

Similar content being viewed by others

References

  1. Sneddon, I.N.: The stress produced by a pulse of pressure moving along the surface of a semi-infinite solid. Rend. del Circ. Mat. di Palermo. 1, 57–62 (1952). https://doi.org/10.1007/BF02843720

    Article  MathSciNet  MATH  Google Scholar 

  2. Cole, J., Huth, J.: Stresses produced in a half plane by moving loads. J. Appl. Mech. 25, 433–436 (1958)

    MathSciNet  MATH  Google Scholar 

  3. Eason, G.: The stresses produced in a semi-infinite solid by a moving surface force. Int. J. Eng. Sci. 2, 581–609 (1965). https://doi.org/10.1016/0020-7225(62)90038-8

    Article  MATH  Google Scholar 

  4. Achenbach, J.D., Keshava, S.P., Herrmann, G.: Moving load on a plate resting on an elastic half space. J. Appl. Mech. 34, 910–914 (1967). https://doi.org/10.1115/1.3607855

    Article  Google Scholar 

  5. Chonan, S.: Moving load on a pre-stressed plate resting on a fluid half-space. Ing. Arch. 45, 171–178 (1976). https://doi.org/10.1007/BF00539779

    Article  MATH  Google Scholar 

  6. Ungar, A.: Wave generation in an elastic half-space by a normal point load moving uniformly over the free surface. Int. J. Eng. Sci. 14, 935–945 (1976). https://doi.org/10.1016/0020-7225(76)90105-1

    Article  MATH  Google Scholar 

  7. Olsson, M.: On the fundamental moving load problem. J. Sound Vib. 145, 299–307 (1991)

    Article  Google Scholar 

  8. Lee, H.P., Ng, T.Y.: Dynamic response of a cracked beam subject to a moving load. Acta Mech. 106, 221–230 (1994). https://doi.org/10.1007/BF01213564

    Article  MATH  Google Scholar 

  9. Jin, B., Liu, H.: Dynamic response of a poroelastic half space to horizontal buried loading. Int. J. Solids Struct. 38, 8053–8064 (2001). https://doi.org/10.1016/S0020-7683(00)00415-7

    Article  MATH  Google Scholar 

  10. Alekseyeva, L.A.: The dynamics of an elastic half-space under the action of a moving load. J. Appl. Math. Mech. 71, 511–518 (2007). https://doi.org/10.1016/J.JAPPMATHMECH.2007.09.005

    Article  MathSciNet  MATH  Google Scholar 

  11. Rogerson, G.A., Fu, Y.B.: An asymptotic analysis of the dispersion relation of a pre-stressed incompressible elastic plate. Acta Mech. 111, 59–74 (1995). https://doi.org/10.1007/BF01187727

    Article  MathSciNet  MATH  Google Scholar 

  12. Kumar, R., Hundal, B.S.: Surface wave propagation in a fluid-saturated incompressible porous medium. Sadhana 32, 155–166 (2007). https://doi.org/10.1007/s12046-007-0014-x

    Article  MATH  Google Scholar 

  13. Biot, M.: Theory of propagation of elastic waves in a fluid-saturated porous solid. I. Low-frequency range. J. Acoust. Soc. Am. 28, 168–178 (1956). https://doi.org/10.1121/1.1908239

    Article  MathSciNet  Google Scholar 

  14. Biot, M.A.: Mechanics of deformation and acoustic propagation in porous media. J. Appl. Phys. 33, 1482–1498 (1962). https://doi.org/10.1063/1.1728759

    Article  MathSciNet  MATH  Google Scholar 

  15. Theodorakopoulos, D.D.: Dynamic analysis of a poroelastic half-plane soil medium under moving loads. Soil Dyn. Earthq. Eng. 23, 521–533 (2003). https://doi.org/10.1016/S0267-7261(03)00074-5

    Article  Google Scholar 

  16. Jin, B.: Dynamic displacements of an infinite beam on a poroelastic half space due to a moving oscillating load. Arch. Appl. Mech. 74, 277–287 (2004). https://doi.org/10.1007/s00419-004-0349-2

    Article  MATH  Google Scholar 

  17. Lu, J.F., Jeng, D.S.: A half-space saturated poro-elastic medium subjected to a moving point load. Int. J. Solids Struct. 44, 573–586 (2007). https://doi.org/10.1016/j.ijsolstr.2006.05.020

    Article  MATH  Google Scholar 

  18. Meissner, R.: The Little Book of Planet Earth. Copernicus, Göttingen (2002)

    Google Scholar 

  19. Mahanty, M., Chattopadhyay, A., Kumar, P., Singh, A.K.: Effect of initial stress, heterogeneity and anisotropy on the propagation of seismic surface waves. Mech. Adv. Mater. Struct. (2018). https://doi.org/10.1080/15376494.2018.1472329

    Article  Google Scholar 

  20. Singh, A.K., Negi, A., Verma, A.K., Kumar, S.: Analysis of stresses induced due to a moving load on irregular initially stressed heterogeneous viscoelastic rock medium. J. Eng. Mech. 143, 04017096 (2017). https://doi.org/10.1061/(ASCE)EM.1943-7889.0001307

    Article  Google Scholar 

  21. Chattopadhyay, A., Saha, S.: Dynamic response of normal moving load in the plane of symmetry of a monoclinic half-space. Tamkang J. Sci. Eng. 9, 307–312 (2006)

    Google Scholar 

  22. Chattopadhyay, A., Gupta, S., Sharma, V.K., Kumari, P.: Stresses produced on a rough irregular half-space by a moving load. Acta Mech. 221, 271–280 (2011). https://doi.org/10.1007/s00707-011-0507-x

    Article  MATH  Google Scholar 

  23. Chattopadhyay, A., Sahu, S.A.: Stresses produced in slightly compressible, finitely deformed elastic media due to a normal moving load. Arch. Appl. Mech. 82, 699–708 (2012). https://doi.org/10.1007/s00419-011-0584-2

    Article  MATH  Google Scholar 

  24. Kaur, T., Kumar Sharma, S., Kumar Singh, A.: Dynamic response of a moving load on a micropolar half-space with irregularity. Appl. Math. Model. 40, 3535–3549 (2016). https://doi.org/10.1016/j.apm.2015.09.102

    Article  MathSciNet  MATH  Google Scholar 

  25. Chatterjee, M., Chattopadhyay, A.: Effect of moving load due to irregularity in ice sheet floating on water. Acta Mech. 228, 1749–1765 (2017). https://doi.org/10.1007/s00707-016-1786-z

    Article  MathSciNet  MATH  Google Scholar 

  26. Mukherjee, S.: Stresses produced by a load moving over the rough boundary of a semi-infinite transversely isotropic solid. Pure Appl. Geophys. 72, 45–50 (1969)

    Article  Google Scholar 

  27. Kumar, P., Chattopadhyay, A., Mahanty, M., Singh, A.K.: Stresses induced by a moving load in a composite structure with an incompressible poroviscoelastic layer. J. Eng. Mech. 145, 04019062 (2019). https://doi.org/10.1061/(asce)em.1943-7889.0001635

    Article  Google Scholar 

  28. Love, A.: A Treatise on the Mathematical Theory of Elasticity. Cambridge University Press, Cambridge (1892)

    MATH  Google Scholar 

  29. Son, M.S., Kang, Y.J.: Propagation of shear waves in a poroelastic layer constrained between two elastic layers. Appl. Math. Model. 36, 3685–3695 (2012). https://doi.org/10.1016/j.apm.2011.11.008

    Article  MathSciNet  MATH  Google Scholar 

  30. Sharma, M.D., Kumar, R., Gogna, M.L.: Surface wave propagation in a transversely isotropic elastic layer overlying a liquid saturated porous solid half-space and lying under the uniform layer of liquid. Pure Appl. Geophys. 133, 523–539 (1990). https://doi.org/10.1007/BF00878003

    Article  Google Scholar 

Download references

Acknowledgements

The authors convey their sincere thanks to Indian Institute of Technology (ISM), Dhanbad, India, for facilitating them with best research facility and for providing a Senior Research Fellowship to Mr. Pulkit Kumar. The authors also express sincere gratitude to the Ministry of Science and Technology, DST, Govt. of India, under Grant No. DST/INSPIRE FELLOWSHIP/IF160054 for providing Senior Research Fellowship to Ms. Moumita Mahanty.

Author information

Authors and Affiliations

  1. Department of Mathematics and Computing, Indian Institute of Technology (Indian School of Mines), Dhanbad, Dhanbad, Jharkhand, 826004, India

    Moumita Mahanty, Pulkit Kumar, Abhishek Kumar Singh & Amares Chattopadhyay

Authors
  1. Moumita Mahanty
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Pulkit Kumar
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Abhishek Kumar Singh
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Amares Chattopadhyay
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Pulkit Kumar.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Appendices

Appendix A

$$\begin{aligned} \overline{P_{10} }= & {} -\frac{R}{\pi D}\left( {\frac{F_{1}^{\left( 0 \right) } }{N_{1}^{\left( 0 \right) } }-2\frac{C_{1}^{\left( 0 \right) } }{N_{1}^{\left( 0 \right) } }\psi _{2} q_{2} } \right) ,\,\,\overline{P_{20} } =\frac{R}{\pi D}\left( {\frac{F_{1}^{\left( 0 \right) } }{N_{1}^{\left( 0 \right) } }-2\frac{C_{1}^{\left( 0 \right) } }{N_{1}^{\left( 0 \right) } }\psi _{1} q_{1} } \right) ,\,\,\overline{Q_{10} } =-\frac{\left( {\psi _{2} +q_{2} } \right) }{\pi D}\frac{G_{1}^{\left( 0 \right) } }{N_{1}^{\left( 0 \right) } },\\ \,\overline{Q_{20} }= & {} \frac{\left( {\psi _{1} +q_{1} } \right) }{\pi D}\frac{G_{1}^{\left( 0 \right) } }{N_{1}^{\left( 0 \right) } },\,\overline{P_{11} } =\overline{P_{10} } f\left( {kq_{1} -\gamma } \right) +\frac{{f}'}{D}\left[ {\overline{Q_{10} } b_{1} +b_{2} \overline{Q_{20} } } \right] ,\\ \overline{P_{21} }= & {} \overline{P_{20} } f\left( {kq_{2} -\gamma } \right) -\frac{{f}'}{D}\left[ {\overline{Q_{10} } b_{3} +b_{4} \overline{Q_{20} } } \right] , \\ \overline{Q_{11} }= & {} \overline{Q_{10} } f\left( {kq_{1} -\gamma } \right) -\frac{{f}'}{D}\left[ {\overline{P_{10} } b_{1} +b_{2} \overline{P_{20} } } \right] ,\,\,\overline{Q_{21} } =\overline{Q_{20} } f\left( {kq_{2} -\gamma } \right) +\frac{{f}'}{D}\left[ {\overline{P_{10} } b_{3} +b_{4} \overline{P_{20} } } \right] , \\ \overline{E_{1} }= & {} \frac{\overline{P_{1} } e^{-kq_{1} H}\left( {\psi _{1} +\chi _{2} } \right) +\overline{P_{2} } e^{-kq_{2} H}\left( {\psi _{2} +\chi _{2} } \right) }{e^{-kr_{1} H}\left( {\chi _{2} -\chi _{1} } \right) },\,\overline{E_{2} } =-\frac{\overline{P_{1} } e^{-kq_{1} H}\left( {\psi _{1} +\chi _{1} } \right) +\overline{P_{2} } e^{-kq_{2} H}\left( {\psi _{2} +\chi _{1} } \right) }{e^{-kr_{2} H}\left( {\chi _{2} -\chi _{1} } \right) },\\ D= & {} \left( {\frac{F_{1}^{\left( 0 \right) } }{N_{1}^{\left( 0 \right) } }-2\frac{C_{1}^{\left( 0 \right) } }{N_{1}^{\left( 0 \right) } }\psi _{1} q_{1} } \right) \frac{G_{1}^{\left( 0 \right) } }{N_{1}^{\left( 0 \right) } }\left( {\psi _{2} +q_{2} } \right) -\left( {\frac{F_{1}^{\left( 0 \right) } }{N_{1}^{\left( 0 \right) } }-2\frac{C_{1}^{\left( 0 \right) } }{N_{1}^{\left( 0 \right) } }\psi _{2} q_{2} } \right) \frac{G_{1}^{\left( 0 \right) } }{N_{1}^{\left( 0 \right) } }\left( {\psi _{1} +q_{1} } \right) ,\,\, \\ b_{1}= & {} \left( {\frac{G_{1}^{\left( 0 \right) } }{N_{1}^{\left( 0 \right) } }} \right) ^{2}\left( {\psi _{1} +q_{1} } \right) \left( {\psi _{2} +q_{2} } \right) +\left( {\frac{F_{1}^{\left( 0 \right) } }{N_{1}^{\left( 0 \right) } }-2\frac{C_{1}^{\left( 0 \right) } }{N_{1}^{\left( 0 \right) } }m_{2} q_{2} } \right) \left( {\left( {2-\frac{A_{1}^{\left( 0 \right) } }{N_{1}^{\left( 0 \right) } }} \right) -\frac{F_{1}^{\left( 0 \right) } }{N_{1}^{\left( 0 \right) } }\psi _{1} q_{1} } \right) , \\ b_{2}= & {} \left( {\frac{G_{1}^{\left( 0 \right) } }{N_{1}^{\left( 0 \right) } }} \right) ^{2}\left( {\psi _{2} +q_{2} } \right) ^{2}+\left( {\frac{F_{1}^{\left( 0 \right) } }{N_{1}^{\left( 0 \right) } }-2\frac{C_{1}^{\left( 0 \right) } }{N_{1}^{\left( 0 \right) } }\psi _{2} q_{2} } \right) \left( {\left( {2-\frac{A_{1}^{\left( 0 \right) } }{N_{1}^{\left( 0 \right) } }} \right) -\frac{F_{1}^{\left( 0 \right) } }{N_{1}^{\left( 0 \right) } }\psi _{2} q_{2} } \right) , \\ b_{3}= & {} \left( {\frac{G_{1}^{\left( 0 \right) } }{N_{1}^{\left( 0 \right) } }} \right) ^{2}\left( {\psi _{1} +q_{1} } \right) ^{2}+\left( {\frac{F_{1}^{\left( 0 \right) } }{N_{1}^{\left( 0 \right) } }-2\frac{C_{1}^{\left( 0 \right) } }{N_{1}^{\left( 0 \right) } }\psi _{1} q_{1} } \right) \left( {\left( {2-\frac{A_{1}^{\left( 0 \right) } }{N_{1}^{\left( 0 \right) } }} \right) -\frac{F_{1}^{\left( 0 \right) } }{N_{1}^{\left( 0 \right) } }\psi _{1} q_{1} } \right) ,\\ b_{1}= & {} \left( {\frac{G_{1}^{\left( 0 \right) } }{N_{1}^{\left( 0 \right) } }} \right) ^{2}\left( {\psi _{1} +q_{1} } \right) \left( {\psi _{2} +q_{2} } \right) +\left( {\frac{F_{1}^{\left( 0 \right) } }{N_{1}^{\left( 0 \right) } }-2\frac{C_{1}^{\left( 0 \right) } }{N_{1}^{\left( 0 \right) } }\psi _{1} q_{1} } \right) \left( {\left( {2-\frac{A_{1}^{\left( 0 \right) } }{N_{1}^{\left( 0 \right) } }} \right) -\frac{F_{1}^{\left( 0 \right) } }{N_{1}^{\left( 0 \right) } }\psi _{2} q_{2} } \right) . \end{aligned}$$

Appendix B

$$\begin{aligned} P_{11}^{\left( 1 \right) }= & {} \overline{P_{10} } fkq_{1} +\frac{{f}'}{D}\left[ {\overline{Q_{10} } b_{1} +b_{2} \overline{Q_{20} } } \right] ,\,P_{21}^{\left( 1 \right) } =\overline{P_{20} } fkq_{2} -\frac{{f}'}{D}\left[ {\overline{Q_{10} } b_{3} +b_{4} \overline{Q_{20} } } \right] , \\ Q_{11}^{\left( 1 \right) }= & {} \overline{Q_{10} } fkq_{1} -\frac{{f}'}{D}\left[ {\overline{P_{10} } b_{1} +b_{2} \overline{P_{20} } } \right] ,\,\,Q_{21}^{\left( 1 \right) } =\overline{Q_{20} } fkq_{2} +\frac{{f}'}{D}\left[ {\overline{P_{10} } b_{3} +b_{4} \overline{P_{20} } } \right] , \\ E_{1}^{\left( 1 \right) }= & {} \frac{P_{1}^{\left( 1 \right) } e^{-kq_{1} H}\left( {\psi _{1} +\chi _{2} } \right) +P_{2}^{\left( 1 \right) } e^{-kq_{2} H}\left( {\psi _{2} +\chi _{2} } \right) }{e^{-kr_{1} H}\left( {\chi _{2} -\chi _{1} } \right) },\\ E_{2}^{\left( 1 \right) }= & {} -\frac{P_{1}^{\left( 1 \right) } e^{-kq_{1} H}\left( {\psi _{1} +\chi _{1} } \right) +P_{2}^{\left( 1 \right) } e^{-kq_{2} H}\left( {\psi _{2} +\chi _{1} } \right) }{e^{-kr_{2} H}\left( {\chi _{2} -\chi _{1} } \right) },\\ E_{1}^{\left( 2 \right) }= & {} \frac{\overline{P_{10} } e^{-kq_{1} H}\left( {\psi _{1} +\chi _{2} } \right) +\overline{P_{20} } e^{-kq_{2} H}\left( {\psi _{2} +\chi _{2} } \right) }{e^{-kr_{1} H}\left( {\chi _{2} -\chi _{1} } \right) },\\ E_{2}^{\left( 2 \right) }= & {} -\frac{\overline{P_{10} } e^{-kq_{1} H}\left( {\psi _{1} +\chi _{1} } \right) +\overline{P_{20} } e^{-kq_{2} H}\left( {\psi _{2} +\chi _{1} } \right) }{e^{-kr_{2} H}\left( {\chi _{2} -\chi _{1} } \right) },\\ P_{10}^{\left( 1 \right) }= & {} -\frac{R}{\pi D}\left( {\frac{\lambda _{1} }{\mu _{1} }-2\frac{\lambda _{1} +2\mu _{1} }{\mu _{1} }\psi _{2} q_{2} } \right) ,\,\,P_{20}^{\left( 1 \right) } =\frac{R}{\pi D}\left( {\frac{\lambda _{1} }{\mu _{1} }-2\frac{\lambda _{1} +2\mu _{1} }{\mu _{1} }\psi _{1} q_{1} } \right) ,\, \\ Q_{10}^{\left( 1 \right) }= & {} -\frac{\left( {\psi _{2} +q_{2} } \right) }{\pi D},Q_{20}^{\left( 1 \right) } =\frac{\left( {\psi _{1} +q_{1} } \right) }{\pi D},\, \\ E_{1}^{\left( 3 \right) }= & {} \frac{P_{10}^{\left( 1 \right) } e^{-kq_{1} H}\left( {\psi _{1} +\chi _{2} } \right) +P_{20}^{\left( 1 \right) } e^{-kq_{2} H}\left( {\psi _{2} +\chi _{2} } \right) }{e^{-kr_{1} H}\left( {\chi _{2} -\chi _{1} } \right) },\\ E_{2}^{\left( 2 \right) }= & {} -\frac{P_{10}^{\left( 1 \right) } e^{-kq_{1} H}\left( {\psi _{1} +\chi _{1} } \right) +P_{20}^{\left( 1 \right) } e^{-kq_{2} H}\left( {\psi _{2} +\chi _{1} } \right) }{e^{-kr_{2} H}\left( {\chi _{2} -\chi _{1} } \right) }. \end{aligned}$$

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Mahanty, M., Kumar, P., Singh, A.K. et al. Dynamic response of an irregular heterogeneous anisotropic poroelastic composite structure due to normal moving load. Acta Mech 231, 2303–2321 (2020). https://doi.org/10.1007/s00707-020-02649-z

Download citation

  • Received:

  • Revised:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00707-020-02649-z

Search

Navigation