Doubly periodic array of coated cylindrical inclusions model and applications for nanocomposites

Abstract

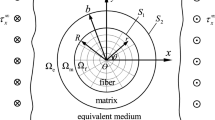
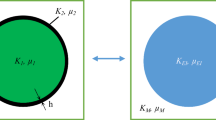
An analytical method is proposed to solve the problem of an infinite elastic matrix containing a doubly periodic array of coated cylindrical inclusions under antiplane shear. The elastic fields in the inclusions, the coatings/interphases and the matrix are derived, which are used to investigate the stresses and the effective stiffness coefficients of the nanofiber composites. Numerical examples demonstrate the size dependence of the stress and the effective stiffness coefficient, and the effects of the interphase thickness and stiffness and array configurations of the inclusions on the effective stiffness coefficient. A finite element analysis is used to benchmark the effective stiffness coefficient predicted by the proposed model, in which excellent agreement is observed. When letting the interphase be thin enough, the proposed coated inclusions model can be used to simulate the zero-thickness interface model, which is validated by the results comparisons of the two models. Instabilities of the stress fields are observed under certain conditions in simulating the zero-thickness interface model.

Appendices

Appendix A

A representative volume element (RVE) of the periodic composites is shown in Fig. 16. The periodic boundary condition can be found in the literature [20, 31] and is written as follows:

$$\begin{aligned} u_i^{j+} -u_i^{j-} =\bar{{\varepsilon }}_{ik} (x_k^{j+} -x_k^{j-} ) \end{aligned}$$

(A.1)

where $u_i^{j+}$ and $u_i^{j-}$ are the $i\hbox {th}$ displacement components for the corresponding points on the two opposite boundary surfaces of the RVE, which are perpendicular to the $x_{j}$-axis (“+” for the positive $x_{j}$ direction, “–” for the $x_{j}$ negative direction), and $\bar{{\varepsilon }}_{ik}$ is the given average strain.

Fig. 16

Solid RVE

The effective properties of a composite determine the relation between its average stresses and strains:

$$\begin{aligned} \left\{ {{\begin{array}{l} {\bar{{\sigma }}_{11} } \\ {\bar{{\sigma }}_{22} } \\ {\bar{{\sigma }}_{33} } \\ {\bar{{\sigma }}_{23} } \\ {\bar{{\sigma }}_{31} } \\ {\mathbf {\sigma }_{12} } \\ \end{array} }} \right\} =\left[ {{\begin{array}{llllll} {C_{11}^{\mathrm{eff}} }&{} {C_{12}^{\mathrm{eff}} }&{} {C_{13}^{\mathrm{eff}} }&{} {C_{14}^{\mathrm{eff}} }&{} {C_{15}^{\mathrm{eff}} }&{} {C_{16}^{\mathrm{eff}} } \\ &{} {C_{22}^{\mathrm{eff}} }&{} {C_{23}^{\mathrm{eff}} }&{} {C_{24}^{\mathrm{eff}} }&{} {C_{25}^{\mathrm{eff}} }&{} {C_{26}^{\mathrm{eff}} } \\ &{} &{} {C_{33}^{\mathrm{eff}} }&{} {C_{34}^{\mathrm{eff}} }&{} {C_{35}^{\mathrm{eff}} }&{} {C_{36}^{\mathrm{eff}} } \\ &{} &{} &{} {C_{44}^{\mathrm{eff}} }&{} {C_{45}^{\mathrm{eff}} }&{} {C_{46}^{\mathrm{eff}} } \\ &{} {SYM}&{} &{} &{} {C_{55}^{\mathrm{eff}} }&{} {C_{56}^{\mathrm{eff}} } \\ &{} &{} &{} &{} &{} {C_{66}^{\mathrm{eff}} } \\ \end{array} }} \right] \left\{ {{\begin{array}{l} {\bar{{\varepsilon }}_{11} } \\ {\bar{{\varepsilon }}_{22} } \\ {\bar{{\varepsilon }}_{33} } \\ {2\bar{{\varepsilon }}_{23} } \\ {2\bar{{\varepsilon }}_{31} } \\ {2\bar{{\varepsilon }}_{12} } \\ \end{array} }} \right\} . \end{aligned}$$

(A.2)

In order to evaluate the effective stiffness coefficients, six independent uniaxial constant strain states, i.e., three pure normal strain states and three pure sliding states, as shown in Eq. (A.3), should be applied to the RVE. Each constant strain state of the RVE is studied out by applying the periodic boundary condition Eq. (A.1) to the RVE boundaries. After determining the average stresses of the RVE corresponding to each constant strain state, the effective stiffness coefficients are calculated from Eq. (A.2),

$$\begin{aligned} \left\{ {{\begin{array}{l} {\bar{{\varepsilon }}_{11} } \\ 0 \\ 0 \\ 0 \\ 0 \\ 0 \\ \end{array} }} \right\} , \quad \left\{ {{\begin{array}{l} 0 \\ {\bar{{\varepsilon }}_{22} } \\ 0 \\ 0 \\ 0 \\ 0 \\ \end{array} }} \right\} , \quad \left\{ {{\begin{array}{l} 0 \\ 0 \\ {\bar{{\varepsilon }}_{33} } \\ 0 \\ 0 \\ 0 \\ \end{array} }} \right\} , \quad \left\{ {{\begin{array}{l} 0 \\ 0 \\ 0 \\ {2\bar{{\varepsilon }}_{23} } \\ 0 \\ 0 \\ \end{array} }} \right\} , \quad \left\{ {{\begin{array}{l} 0 \\ 0 \\ 0 \\ 0 \\ {2\bar{{\varepsilon }}_{31} } \\ 0 \\ \end{array} }} \right\} , \quad \left\{ {{\begin{array}{l} 0 \\ 0 \\ 0 \\ 0 \\ 0 \\ {2\bar{{\varepsilon }}_{12} } \\ \end{array} }} \right\} . \end{aligned}$$

(A.3)

To apply the periodic boundary conditions, the meshes in the opposite boundary surfaces of the RVE must be the same. For each pair of displacement component at two corresponding nodes on the two opposite boundary surfaces, a constraint equation is established. Although a large number of the constraint equations need to be established, it is easy to carry it out by using automatic schemes and APDL (ANSYS Programming Design Language) embedded in software package ANSYS.

For the antiplane problem, only the antiplane displacement $u_3$ is not equal to zero in the periodic boundary condition Eq. (A.1), and the antiplane average strains $\bar{{\varepsilon }}_{13}$ and $\bar{{\varepsilon }}_{23}$ need to be given in Eq. (A.2). In the present paper, the mesh was generated using the three-dimensional element Solid45. To reduce calculative time, only one element layer was set along the ${x}_{3}\hbox {-axis}$.

Appendix B

When the area of unit cell S tends to infinity, $\zeta (z)\approx \frac{1}{z}$, Eqs. (37) and (39) are degraded to

$$\begin{aligned} \tau _f= & {} \tau ^{\infty }+2G_m \sum _{k=1}^\infty {kA_k z^{k-1}} +G_m \sum _{k=1}^\infty {k\left[ {\left( {R_2^{-2k} -R_1^{-2k} } \right) \bar{{B}}_{-k} -A_k } \right] z^{k-1}}, \end{aligned}$$

(B.1)

$$\begin{aligned} \tau _m= & {} \tau ^{\infty }+G_m \sum _{k=1}^\infty {\frac{(-1)^{k}}{(k-1)!}\left[ {\bar{{A}}_k R_1^{2k} +\bar{{B}}_k \left( {R_2^{2k} -R_1^{2k} } \right) } \right] \left( {\frac{1}{z}} \right) ^{(k)}}. \end{aligned}$$

(B.2)

Equations (40) and (41) are degraded to

$$\begin{aligned}&\left( {\frac{1}{G_f }-\frac{1}{G_m }} \right) \tau ^{\infty }+\left( {\frac{1}{G_f }-\frac{1}{G_m }} \right) G_m \sum _{k=1}^\infty {k\left[ {\left( {R_2^{-2k} -R_1^{-2k} } \right) \bar{{B}}_{-k} -A_k } \right] z^{k-1}}\nonumber \\&\qquad +\,\frac{2G_m \sum _{k=1}^\infty {kA_k z^{k-1}} }{G_f }=0, \end{aligned}$$

(B.3)

$$\begin{aligned}&\left( {\frac{1}{G_p }-\frac{1}{G_m }} \right) \tau ^{\infty }-\left( {\frac{1}{G_p }-\frac{1}{G_m }} \right) G_m \sum _{k=1}^\infty {\left[ {k\left( {B_k -\bar{{B}}_{-k} R_2^{-2k} } \right) z^{k-1}} \right] } +2\frac{G_m }{G_p }\sum _{k=1}^\infty {kB_k z^{k-1}} \nonumber \\&\qquad +\,\left( {\frac{1}{G_p }-\frac{1}{G_m }} \right) G_m \sum _{k=1}^\infty {\frac{(-1)^{k}}{(k-1)!}\left[ {\left( {\bar{{A}}_k -\bar{{B}}_k } \right) R_1^{2k} +B_{-k} } \right] \left( {\frac{1}{z}} \right) ^{(k)}}\nonumber \\&\qquad -\,2\frac{G_m }{G_p }\sum _{k=1}^\infty {\left( {kB_{-k} z^{-(k+1)}} \right) } =0. \end{aligned}$$

(B.4)

From Eqs. (B.3) and (B.4), one obtains

$$\begin{aligned}&\left( {\frac{1}{G_f }-\frac{1}{G_m }} \right) \tau ^{\infty }+\left( {\frac{1}{G_f }-\frac{1}{G_m }} \right) G_m \left[ {\left( {R_2^{-2} -R_1^{-2} } \right) \bar{{B}}_{-1} -A_1 } \right] +2\frac{G_m }{G_f }A_1 =0, \end{aligned}$$

(B.5)

$$\begin{aligned}&\left( {\frac{1}{G_f }-\frac{1}{G_m }} \right) G_m \left[ {\left( {R_2^{-2k} -R_1^{-2k} } \right) \bar{{B}}_{-k} -A_k } \right] +2\frac{G_m }{G_f }A_k =0 \quad k\ge 2, \end{aligned}$$

(B.6)

$$\begin{aligned}&\left( {\frac{1}{G_p }-\frac{1}{G_m }} \right) \tau ^{\infty }-\left( {\frac{1}{G_p }-\frac{1}{G_m }} \right) G_m \left( {B_1 -\bar{{B}}_{-1} R_2^{-2} } \right) +2\frac{G_m }{G_p }B_1 =0, \end{aligned}$$

(B.7)

$$\begin{aligned}&\left( {\frac{1}{G_p }-\frac{1}{G_m }} \right) \left[ {\left( {\bar{{A}}_1 -\bar{{B}}_1 } \right) R_1^2 +B_{-1} } \right] -\frac{2}{G_p }B_{-1} =0, \end{aligned}$$

(B.8)

$$\begin{aligned}&\left( {\frac{1}{G_p }-\frac{1}{G_m }} \right) \left( {B_k -\bar{{B}}_{-k} R^{-2k}} \right) -\frac{2}{G_p }B_k =0 \quad k\ge 2, \end{aligned}$$

(B.9)

$$\begin{aligned}&\left( {\frac{1}{G_p }-\frac{1}{G_m }} \right) \left[ {\left( {\bar{{A}}_k -\bar{{B}}_k } \right) R_1^{2k} +B_{-k} } \right] -\frac{2}{G_p }B_{-k} =0 \quad k\ge 2. \end{aligned}$$

(B.10)

From Eqs. (B.6), (B.9) and (B.10), one obtains $A_k =B_k =B_{-k} =0$$(k\ge 2)$. By letting $G_p =\frac{G_s }{R_2 -R_1 }$, $A_1$, $B_1$ and $B_{-1}$ can be determined by Eqs. (B.5), (B.7) and (B.8) as follows:

$$\begin{aligned} A_1= & {} \frac{2(G_f -G_m )G_s R_2^2 \tau ^{\infty }}{\varDelta }, \end{aligned}$$

(B.11)

$$\begin{aligned} B_1= & {} \frac{R_2^2 \left[ {G_s +G_f \left( {R_2 -R_1 } \right) } \right] \left[ {G_m \left( {R_2 -R_1 } \right) -G_s } \right] \tau ^{\infty }}{\left( {R_1 -R_2 } \right) \varDelta }, \end{aligned}$$

(B.12)

$$\begin{aligned} B_{-1}= & {} \frac{R_1^2 R_2^2 \left[ {G_f \left( {R_2 -R_1 } \right) -G_s } \right] \left[ {G_m \left( {R_1 -R_2 } \right) +G_s } \right] \bar{{\tau }}^{\infty }}{\left( {R_1 -R_2 } \right) \varDelta } \end{aligned}$$

(B.13)

where $\varDelta =G_m \left[ {G_s^2 \left( {R_1 +R_2 } \right) +G_f G_m \left( {R_1 -R_2 } \right) ^{2}\left( {R_1 +R_2 } \right) +G_s \left( {G_f +G_m } \right) \left( {R_1^2 +R_2^2 } \right) } \right]$.

Noting $A_k =B_k =B_{-k} =0$$(k\ge 2)$, inserting Eqs. (B.11)–(B.13) into Eqs. (B.1) and (B.2) and letting $R_1 \rightarrow R$ and $R_2 \rightarrow R$ yield

$$\begin{aligned} \tau _f= & {} \frac{2G_f \tau ^{\infty }}{G_f +G_m +{G_s }/R}, \end{aligned}$$

(B.14)

$$\begin{aligned} \tau _m= & {} \tau ^{\infty }+\frac{G_f -G_m +{G_s }/R}{G_f +G_m +{G_s }/R}\frac{R^{2}}{z^{2}}\bar{{\tau }}^{\infty } \end{aligned}$$

(B.15)

which are coincident with the results in Ref. [32].