Skip to main content
SpringerLink
Log in

Lagrange’s equations for open systems, derived via the method of fictitious particles, and written in the Lagrange description of continuum mechanics

  • Published:
Acta Mechanica Aims and scope Submit manuscript

Abstract

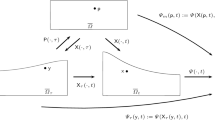
In the present paper, a formulation of Lagrange’s equations, written in the framework of the Lagrange (material) description of Continuum Mechanics, is provided for open systems. An open system is constituted by (the portion of) a continuous material body that is enclosed by a nonmaterial surface. Such a surface, through which a flow of mass takes place, is also denoted as a control surface, and the corresponding volume is called a control volume. In order to apply Lagrange’s equations of analytical mechanics, the motion and the deformation of the body is modeled in the framework of the Ritz approximation technique by means of a finite number of generalized coordinates. However, since mass may not be conserved in an open system due to the flow of mass through the control surface, the original form of Lagrange’s equations must be accomplished by proper flux terms to be considered at the control surface. In order to derive this extended form, a local version of Lagrange’s equations is derived first, using a proper mathematical manipulation of the local relation of balance of linear momentum written in the Lagrange description of Continuum Mechanics. This local form is integrated over the volume that instantaneously is enclosed by the image of the control surface in a properly chosen reference configuration. In the integrated form, the Truesdell–Toupin method of fictitious particles and generalized Reynolds transport theorems are utilized in order to exchange the integrals and the partial derivatives with respect to time and generalized coordinates and velocities. This yields the desired form of Lagrange’s equations for open systems, written in the Lagrange description of Continuum Mechanics. Illustrative examples demonstrate the consistence of this novel form with the Euler (spatial) version of Lagrange’s equations for open systems, which was derived earlier by the present authors.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Dugas R.: A History of Mechanics. Dover, New York (1988)

    MATH  Google Scholar 

  2. Casey J.: Geometrical derivation of Lagrange’s equations for a system of particles. Am. J. Phys. 62, 836–847 (1994)

    Article  MathSciNet  MATH  Google Scholar 

  3. Shabana A.A.: Dynamics of Multibody Systems, 3rd edn. Cambridge University Press, Cambridge (2005)

    Book  Google Scholar 

  4. Gignoux C., Silvestre-Brac B.: Solved Problems in Lagrangian and Hamiltonian Mechanics. Springer, Dordrecht (2009)

    Book  MATH  Google Scholar 

  5. Ziegler F.: Mechanics of Solids and Fluids, 2nd edn, 2nd print. Springer, New York (1998)

    Google Scholar 

  6. Leissa A.W.: The historical bases of the Rayleigh and Rayleigh–Ritz methods. J. Sound Vib. 287, 961–978 (2005)

    Article  Google Scholar 

  7. Goldstein H., Poole Ch., Safko J.: Classical Mechanics, 3rd edn. Addison Wesley, San Francisco (2002)

    Google Scholar 

  8. Washizu K.: Variational Methods in Elasticity and Plasticity, 2nd edn. Pergamon Press, Oxford (1974)

    Google Scholar 

  9. Truesdell, C., Toupin, R.A.: The classical field theories. In: Flügge, S. (ed.) Handbuch der Physik, vol. II/l: Prinzipien der klassischen Mechanik und Feldtheorie, pp. 226–793. Springer, Berlin (1960)

  10. Irschik, H., Holl, H. J., Hammelmüller, F.: The Rayleigh–Ritz technique and the Lagrange equations in Continuum Mechanics: formulations for material and non-material volumes. In: Irschik, H., Schlacher, K. (eds.) Advanced Dynamics and Control of Structures and Machines, CISM Courses and Lectures, vol. 444, pp. 21–36. Springer, Wien, New York (2004)

  11. Irschik H., Holl H.J.: Mechanics of variable-mass systems—Part 1: balance of mass and linear momentum. ASME Appl. Mech. Rev. 57, 145–160 (2004)

    Article  Google Scholar 

  12. Cveticanin L.: Dynamics of Machines with Variable Mass. Gordon and Breach Science, London (1998)

    MATH  Google Scholar 

  13. Mušicki D.: General energy change law for systems with variable mass. Eur. J. Mech. A/Solids 18, 719–730 (1999)

    Article  MathSciNet  MATH  Google Scholar 

  14. Cveticanin L.: Conservation laws in systems with variable mass. ASME J. Appl. Mech. 60, 954–959 (1993)

    Article  MathSciNet  MATH  Google Scholar 

  15. Pesce C.P.: The application of Lagrange equations to mechanical systems with mass explicitly dependent on position. ASME J. Appl. Mech. 70, 751–756 (2003)

    Article  MATH  Google Scholar 

  16. Pesce C.P., Tannuri E.A., Casetta L.: The Lagrange equations for systems with mass varying explicitly with position: some applications to offshore engineering. J. Braz. Soc. Mech. Sci. Eng. 28, 496–504 (2006)

    Article  Google Scholar 

  17. Irschik H., Holl H.J.: Lagrange’s equations written for a non-material volume. Acta Mech. 153, 231–248 (2002)

    Article  MATH  Google Scholar 

  18. Irschik, H., Holl, H.J.: On Langrange’s equations for open systems. In: Beskos, D.E., Stavroulakis, G.E. (eds.) CD-Rom Proceedings 10th HSTAM International Congress on Mechanics 2013, Chania, Crete, Greece, 25–27 May 2013, Invited Plenary Lecture (2013)

  19. Ziegler F.: Didaktische Aspekte in mechanischen Erhaltungssätzen. GAMM-Mitteilungen 21, 61–72 (1998)

    MATH  Google Scholar 

  20. Stangl M., Gerstmayr J., Irschik H.: An alternative approach for the analysis of non-linear vibrations of pipes conveying fluid. J. Sound Vib. 310, 493–511 (2008)

    Article  Google Scholar 

  21. Stangl M., Gerstmayr J., Irschik H.: A large deformation planar finite element for pipes conveying fluid based on the absolute nodal coordinate formulation. ASME J. Comput. Nonlinear Dyn. 4, 0310091–0310098 (2009)

    Article  Google Scholar 

  22. Païdoussis, M.P.: Fluid–structure interactions: slender structures and axial flow, vol. 1. Academic Press, London (1998), 2nd edn (2013)

  23. Ghayesh M.H., Païdoussis M.P., Amabili M.: Nonlinear dynamics of cantilevered extensible pipes conveying fluid. J. Sound Vib. 332, 6405–6418 (2013)

    Article  Google Scholar 

  24. Irschik H.: On rational treatments of the general laws of balance and jump, with emphasis on configurational formulations. Acta Mech. 194, 11–32 (2007)

    Article  MATH  Google Scholar 

  25. Casey J.: A basic power decomposition in Lagrangian mechanics. ASME J. Appl. Mech. 71, 735–738 (2004)

    Article  MATH  Google Scholar 

  26. Casetta L., Pesce C.P.: On Seliger and Whitham’s variational principle from the point of view of open hydrodynamic systems. Acta Mech. 219, 181–184 (2011)

    Article  MATH  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Institute of Technical Mechanics, Johannes Kepler University of Linz, Altenbergerstr. 69, 4040, Linz, Austria

    Hans Irschik & Helmut J. Holl

Authors
  1. Hans Irschik
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Helmut J. Holl
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Hans Irschik.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Irschik, H., Holl, H.J. Lagrange’s equations for open systems, derived via the method of fictitious particles, and written in the Lagrange description of continuum mechanics. Acta Mech 226, 63–79 (2015). https://doi.org/10.1007/s00707-014-1147-8

Download citation

  • Received:

  • Revised:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00707-014-1147-8

Keywords

Search

Navigation