Skip to main content
SpringerLink
Log in

Three-dimensional multi-field equations of a functionally graded piezoelectric thick shell with variable thickness, curvature and arbitrary nonhomogeneity

  • Published:
Acta Mechanica Aims and scope Submit manuscript

Abstract

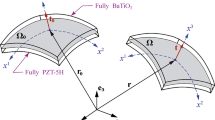
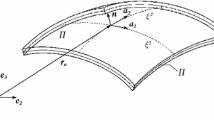
The present research develops a three-dimensional multi-field formulation of a functionally graded piezoelectric thick shell of revolution by using tensor analysis. An orthogonal curvilinear coordinate system was employed, and basic geometric equations were derived for an arbitrary thick shell of revolution with variable thickness and curvature. Mechanical and electrical properties were assumed to vary along a three-dimensional orthogonal coordinate system with arbitrary functional distribution. The functional of the introduced shell was derived by using kinetic and potential energy of the structure based on three orthogonal displacement components, electric potential and material properties. The final differential equations were derived in general state for every arbitrary structure and material property distributions. The obtained equations were reduced for functionally graded and functionally graded piezoelectric cylindrical shells and the mentioned reduced equations were verified by comparison with the literature. Trueness and generality of the present results can be justified by capability of these equations for different geometries and material properties.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

Abbreviations

A i , B i , C i (i = 1, . . . , 40), D i (i = 1, . . . , 39):

The coefficients of the partial time-dependent differential equation of system

C ijkl :

Elastic stiffness coefficient

D i :

Physical components of electric displacement

E :

Modulus of elasticity

\({\vec{E}, E_i }\) :

Vector and components of electric field, respectively

e ijk :

Piezoelectric coefficient

\({F(u_\psi, u_z, u_\theta, \phi, t)}\) :

Functional of the system

g i :

Covariant base vector

g i :

Contra-variant base vector

g ij :

Covariant metric vector

g ij :

Contra-variant metric vector

l :

Nonhomogenous index

r :

Radius of revolution for any arbitrary point

\({\overline r }\) :

Radius of revolution of mid-plane

ds :

Differential distance in meridian direction

S i , S ij :

A symbolic tensor of order one and two, respectively.

\({u_\psi, u_z, u_\theta }\) :

Orthogonal components of displacement in orthogonal coordinate system

\({\overline u }\) :

Total energy per unit volume of the structure

\({\overline u_p }\) :

Potential energy per unit volume of the structure

\({\overline u_k }\) :

Kinetic energy per unit volume of the structure

\({\dot {u}_\psi, \dot {u}_z, \dot {u}_\theta }\) :

Velocity components in the curvilinear coordinate system

dV :

Unit volume of the structure

X :

Position vector of an arbitrary point

q i , X i :

Component of position vector in Cartesian coordinate system

y :

Vertical distance of mid-plane

z :

Second component in the curvilinear coordinate system that describes normal distance of an arbitrary point from the mid-plane

v :

Poisson ratio

\({\psi }\) :

First component in the curvilinear coordinate system that describes the angle between normal to mid-plane and vertical axis (axis of revolution)

θ :

Third component in the curvilinear coordinate system that describes circumferential direction and its angle

\({\rho_\psi }\) :

Distance between mid-plane and axis of revolution along normal to mid-plane

ρ θ :

Meridian radius of curvature

ρ 1 :

\({=\rho_\psi +z}\)

ρ 2 :

 = ρ θ + z

\({\Gamma_{ijk}, \Gamma_{ij}^{k}}\) :

Christoffel symbols of first and second kind

γ ij :

Tensor component of strain

\({\varepsilon_{ij}}\) :

Physical component of strain

\({\phi }\) :

Electric potential

σ ij :

Physical components of stress tensor

η ij :

Dielectric coefficient

\({\vec{\nabla}}\) :

Del operator

\({\|\|}\) :

Describes the magnitude of a component

References

  1. Arciniega R.A., Reddy J.N.: Tensor-based finite element formulation for geometrically nonlinear analysis of shell structures. Comput. Method Appl. Mech. Eng. 196, 1048–1073 (2007)

    Article  MATH  MathSciNet  Google Scholar 

  2. Arciniega R.A., Reddy J.N.: Large deformation analysis of functionally graded shells. Int. J. Solid Struct. 44, 2036–2052 (2007)

    Article  MATH  Google Scholar 

  3. Babaei M.H., Chen Z.T.: Exact solutions for radially polarized and magnetized magnetoelectroelastic rotating cylinders. Smart Mater. Struct. 17, 025035 (2008)

    Article  Google Scholar 

  4. Brischetto S., Carrera E.: Re_ned 2D models for the analysis of functionally graded piezoelectric plates. J. Intell. Mater. Syst. Struct. 20(15), 1783–1797 (2009)

    Article  Google Scholar 

  5. Chen W.Q., Lu Y., Ye J.R., Cai J.B.: 3D electroelastic fields in a functionally graded piezoceramic hollow sphere under mechanical and electric loading. Arch. Appl. Mech. 72, 39–51 (2002)

    Article  MATH  Google Scholar 

  6. Carrera E., Brischetto S.: Piezoelectric shell theories with a priori continuous transverse electromechanical variables. J. Mech. Mater. Struct. 2(2), 377–399 (2007)

    Article  Google Scholar 

  7. Carrera E., Brischetto S.: Reissner mixed theorem applied to static analysis of piezoelectric shells. J. Intell. Mater. Syst. Struct. 18(10), 1083–1107 (2007)

    Article  Google Scholar 

  8. Dai H.L., Fu Y.M., Yang J.H.: Electromagnetoelastic behaviors of functionally graded piezoelectric solid cylinder and sphere. Acta Mech. Solida Sin. 23, 55–63 (2007)

    Article  MATH  Google Scholar 

  9. Dai H.L., Hong L., Fu Y.M., Xiao X.: Analytical solution for electromagnetothermoelastic behaviors of a functionally graded piezoelectric hollow cylinder. Appl. Math. Model. 34, 343–357 (2010)

    Article  MATH  MathSciNet  Google Scholar 

  10. Ghannad K.M., Rahimi G.H., Esmaeilzadeh Kh.S.: General plane elasticity solution of axisymmetric functionally graded thick cylindrical shell. Tech. Eng. J. Modares (in Persian) 10(3), 31–43 (2010)

    Google Scholar 

  11. Jabbari M., Sohrabpour S., Eslami M.R.: Mechanical and thermal stresses in a functionally graded hollow cylinder due to radially symmetric loads. Int. J. Press. Vessel Pip. 79, 493–497 (2002)

    Article  Google Scholar 

  12. Jabbari M., Bahtui A., Eslami M.R.: Axisymmetric mechanical and thermal stresses in thick short length FGM cylinders. Int. J. Press. Vessel Pip. 86, 296–306 (2009)

    Article  Google Scholar 

  13. Kang J.H.: Field equations, equations of motion, and energy functionals for thick shells of revolution with arbitrary curvature and variable thickness from a three-dimensional theory. Acta Mech. 188, 21–37 (2007)

    Article  MATH  Google Scholar 

  14. Khoshgoftar M.J., Ghorbanpour Arani A., Arefi M.: Thermoelastic analysis of a thick walled cylinder made of functionally graded piezoelectric material. Smart Mater. Struct. 18, 115007 (2009)

    Article  Google Scholar 

  15. Liu X., Wang Q., Quek S.T.: Analytical solution for free vibration of piezoelectric coupled moderately thick circular plates. Int. J. Solid Struct. 39, 2129–2151 (2002)

    Article  MATH  Google Scholar 

  16. Lu P., Lee H.P., Lu C.: An exact solution for functionally graded piezoelectric laminated in cylindrical bending. Int. J. Mech. Sci. 47, 437–458 (2005)

    Article  MATH  Google Scholar 

  17. Peng-Fei H., Andrew Y.T.: The transient responses of magneto-electro-elastic hollow cylinders. Smart Mater. Struct. 13, 762–776 (2004)

    Article  Google Scholar 

  18. Rahimi G.H., Arefi M., Khoshgoftar M.J.: Application and analysis of functionally graded piezoelectrical rotating cylinder as mechanical sensor subjected to pressure and thermal loads. Appl. Math. Mech. (Engl. Ed.) 32(8), 997–1008 (2011)

    Article  Google Scholar 

  19. Ray M.C., Reddy J.N.: Active control of laminated cylindrical shells using piezoelectric fiber reinforced composites. Compos. Sci. Technol. 65, 1226–1236 (2005)

    Article  Google Scholar 

  20. Sheng G.G., Wang X.: Thermoelastic vibration and buckling analysis of functionally graded piezoelectric cylindrical shells. Appl. Math. Model. 34, 2630–2643 (2010)

    Article  MATH  MathSciNet  Google Scholar 

  21. Santos H., Mota Soares C.M., Mota Soares C.A., Reddy J.N.: A finite element model for the analysis of 3D axisymmetric laminated shells with piezoelectric sensors and actuators: bending and free vibrations. Comput. Struct. 86, 940–947 (2008)

    Article  Google Scholar 

  22. Yamanouchi, M., Koizumi, M. Shiota, I.: Proceedings of the First International Symposium on Functionally Gradient Materials. Sendai, Japan (1990)

Download references

Author information

Authors and Affiliations

  1. Department of Mechanical Engineering, Tarbiat Modares University, 14115-143, Tehran, Iran

    Mohammad Arefi & G. H. Rahimi

Authors
  1. Mohammad Arefi
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. G. H. Rahimi
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to G. H. Rahimi.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Arefi, M., Rahimi, G.H. Three-dimensional multi-field equations of a functionally graded piezoelectric thick shell with variable thickness, curvature and arbitrary nonhomogeneity. Acta Mech 223, 63–79 (2012). https://doi.org/10.1007/s00707-011-0536-5

Download citation

  • Received:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00707-011-0536-5

Keywords

Search

Navigation