Abstract
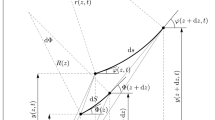
In the proposed paper, a new problem on the steady-state oscillations of an elastic infinite cone is solved for the point oscillating force enclosed to a cone’s vertex. On a cone’s conic surface, the stresses are given. The auxiliary problem for a cone truncated by a spherical surface is formulated with the aim to obtain the solution of the initial problem. The solution is constructed with the help of the integral transformation method and the method of Green’s function. The limiting transition in the solution’s formulas is carried out to obtain the exact solution of the initial problem. The calculation of the displacements and the stress wave field of the cone is performed.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
References
Achenbach J.D.: Wave propagation in elastic solids. North-Holland Publishing Co, Amsterdam (1973)
Grinchenko V.T.: The equilibrium and oscillations of the finite size bodies (in Russian). Naukova Dumka, Kiev (1978)
Babeshko V.A., Glushkov E.I., Zinchenko G.F.: The dynamic of the nonhomogenous linear elastic mediums (in Russian). Nauka, Moscow (1989)
Guz A.N., Kubenko V.D.: The theory of the shells’ non-stationary aerohydroelasticity (in Russian). Naukova Dumka, Kiev (1982)
Harris J.G.: Linear elastic waves. Cambridge Texts in Applied Mathematics, Cambridge (2001)
Bogy D.B., Wang K.C.: Plane steady vibrations of an elastic wedge. J. Elast. 5, 1–16 (1975)
Panasuk V.V., Savruk M.P., Nazarchuk Z.T.: Singular integral equations’ method in the twodimensional elasticity problems of diffraction (in Russian). Naukova Dumka, Kiev (1984)
Bardzokas D.I., Zobnin A.I., Senik A., Filshtinsky M.L.: Mathematical modelling in the problems of the mechanics of coupled fields (in Russian). URSS, Moscow (2005)
Xu R.Q.: Three-dimensional exact solutions for the free vibration of laminated transversely isotropic circular, annular and sectorial plates with unusual boundary conditions. Arch Appl. Mech. 78, 543–558 (2008)
Mykhas’kiv V.V., Khay O.M., Zhang Ch., Bostrom A.: Effective dynamic properties of 3D composite materials containing rigid penny-shaped inclusions. Waves Random Complex Media 20, 491–510 (2010)
Rayleigh J.W.: On waves propagated along the plane surface of an elastic solid. Proc. Lond. Math. Soc. 17, 4–11 (1885)
Nowacki W.: Teoria sprezystosci. Panstwowe Wydawnictwo Naukowe, Warszawa (1970)
Michel, J.H.: Some elementary distributions of stress in three dimensions. Proc. Lond. Math. Soc. Lond, 34, 24–29 (1901)
Love A.H.: A treatise on the mathematical theory of elasticity. The university press, Cambridge (1927)
Popov G.Ya.: About new transformations of the elasticity resolving equations and the new integral transformations with their application to the boundary problems of mechanics. Int. Appl. Mech. 39, 1046–1071 (2003)
Popov G.Ya: Problems of stress concentration in the neighborhood of a spherical defect. Adv. Mech. 15, 71–110 (1992)
Popov G.Ya.: The elastic stress’ concentration around dies, cuts, thin inclusions and reinforcements (in Russian). Nauka, Moskow (1982)
Popov G.Ya.: About expansion of the integral transformations’ method possibilities on the mechanics problems’ solving. J. Appl. Math. Mech. 44, 427–439 (1980)
Bateman H., Erdely A.: Higher transcendental functions, vol 2. McGraw-Hill, NY (1955)
Gradshtein L., Ryzhik L.: The tables of integrals, series and products (in Russian). Nauka, Moscow (1963)
Abramowitz M., Stegun I.: Handbook of mathematical functions. Government Print, USA (1964)
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Popov, G., Vaysfel’d, N. The steady-state oscillations of the elastic infinite cone loaded at a vertex by a concentrated force. Acta Mech 221, 261–270 (2011). https://doi.org/10.1007/s00707-011-0501-3
Received:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00707-011-0501-3