Skip to main content
SpringerLink
Log in

Asymptotic Lyapunov stability with probability one of Duffing oscillator subject to time-delayed feedback control and bounded noise excitation

  • Published:
Acta Mechanica Aims and scope Submit manuscript

Abstract

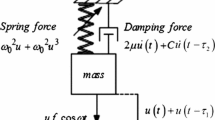
The asymptotic Lyapunov stability with probability one of a Duffing system with time-delayed feedback control under bounded noise parametric excitation is studied. First, the time-delayed feedback control force is expressed approximately in terms of the system state variables without time delay. Then, the averaged Itô stochastic differential equations for the system are derived by using the stochastic averaging method and the expression for the Lyapunov exponent of the linearized averaged Itô equations is derived. It is inferred that the Lyapunov exponent so obtained is the first approximation of the largest Lyapunov exponent of the original system, and the asymptotic Lyapunov stability with probability one of the original system can be determined approximately by using the Lyapunov exponent. Finally, the effects of time delay in feedback control on the Lyapunov exponent and the stability of the system are analyzed. The theoretical results are well verified through digital simulation.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Malek-Zavarei M., Jamshidi M.: Time-Delay Systems: Analysis, Optimization and Applications. North-Holland, New York (1987)

    MATH  Google Scholar 

  2. Stepan G.: Retarded Dynamical Systems: Stability and Characteristic Functions. Longman Scientific and Technical, Essex (1989)

    MATH  Google Scholar 

  3. Hu H.Y., Wang Z.H.: Dynamics of Controlled Mechanical Systems with Delayed Feedback. Springer, Berlin (2002)

    MATH  Google Scholar 

  4. Agrawal A.K., Yang J.N.: Effect of fixed time delay on stability and performance of actively controlled civil engineering structures. Earthquake Eng. Struct. Dyn. 26, 1169–1185 (1997)

    Article  Google Scholar 

  5. Hu H.Y., Dowell E.H., Virgin L.N.: Resonances of a harmonically forced Duffing oscillator with time delay state feedback. Nonlin. Dyn. 15, 311–327 (1998)

    Article  MATH  Google Scholar 

  6. Pu J.P.: Time delay compensation in active control of structure. ASCE J. Eng. Mech. 124, 1018–1028 (1998)

    Article  Google Scholar 

  7. Xua J., Chungb K.W.: Effects of time delayed position feedback on a van der Pol–Duffing oscillator. Physica D 180, 17–39 (2003)

    Article  MathSciNet  Google Scholar 

  8. Wang H.L., Wang Z.H., Hu H.Y.: Hopf bifurcation of an oscillator with quadratic and cubic nonlinearities and with delayed velocity feedback. Acta Mech Sin. 20, 426–434 (2004)

    Article  Google Scholar 

  9. Li X.Y., Ji J.C., Hansen C.H., Tan C.X.: The response of a Duffing-van der Pol oscillator under delayed feedback control. J. Sound Vib. 291, 644–655 (2006)

    Article  MathSciNet  Google Scholar 

  10. Ji J.C., Hansen C.H.: Stability and dynamics of a controlled van der Pol–Duffing oscillator. Chaos Solitons Fract. 28, 555–570 (2006)

    Article  MATH  MathSciNet  Google Scholar 

  11. Di Paola M., Pirrotta A.: Time delay induced effects on control of linear systems under random excitation. Probab. Eng. Mech. 16, 43–51 (2001)

    Article  Google Scholar 

  12. Bilello C., Di Paola M., Pirrotta A.: Time delay induced effects on control of non-linear systems under random excitation. Meccanica 37, 207–220 (2002)

    Article  MATH  MathSciNet  Google Scholar 

  13. Liu Z.H., Zhu W.Q.: Stochastic averaging of quasi-integrable Hamiltonian systems with delayed feedback control. J. Sound Vib. 299, 178–195 (2007)

    Article  MathSciNet  Google Scholar 

  14. Dimentberg, M.F.: A stochastic model of parametric excitation of a straight pipe due to slug flow of a two-phase fluid. In: Proceedings of the Fifth International Conference on Flow-Induced Vibrations, pp. 207–209, Brighton, UK (1991)

  15. Dimentberg M.F.: Stability and subcritical dynamics of structures with spatially disordered parametric excitation. Probab. Eng. Mech. 7, 131–134 (1992)

    Article  Google Scholar 

  16. Li Q.C., Lin Y.K.: New stochastic theory for bridge stability in turbulent flow, II. J. Eng. Mech. 121, 102–116 (1995)

    Article  Google Scholar 

  17. Ariaratnam S.T.: Stochastic stability of viscoelastic systems under bounded noise excitation. In: Naess, A., Krenk, S. (eds) Proceedings of the IUTAM Symposium on Advances in Non-linear Stochastic Mechanics, Kluwer, Dordrecht (1995)

    Google Scholar 

  18. Ariaratnam S.T., Abdelrahman N.M.: Stochastic stability of non-gyroscopic viscoelastic systems. Int. J. Solids Struct. 41, 2685–2709 (2004)

    Article  MATH  Google Scholar 

  19. Huang Z.L., Zhu W.Q., Ni Y.Q., Ko J.M.: Stochastic averaging of strongly non-linear oscillators under bounded noise excitation. J. Sound Vib. 254, 245–267 (2002)

    Article  MathSciNet  Google Scholar 

  20. Yang X., Xu W., Sun Z., Xu Y.: Responses of strongly non-linear oscillator parametrically excited by random narrow-band noise. Appl. Math. Comput. 171, 885–899 (2005)

    Article  MATH  MathSciNet  Google Scholar 

  21. Rong H.W., Meng G., Xu W., Fang T.: Response statistics of three-degree-of-freedom nonlinear system to narrow-band random excitation. Nonlin. Dyn. 32, 93–107 (2003)

    Article  MATH  MathSciNet  Google Scholar 

  22. Hein H., Lepik U.: Response of nonlinear oscillators with random frequency of excitation, revisited. J. Sound Vib. 301, 1040–1049 (2007)

    Article  Google Scholar 

  23. Khasminskii R.Z.: Sufficient and necessary conditions of almost sure asymptotic stability of a linear stochastic system. Theory Probab. Appl. 11, 390–405 (1967)

    Article  Google Scholar 

  24. Oseledec V.I.: A multiplicative ergodic theorem: Lyapunov characteristic number for dynamical systems. Trans. Moscow Math. Soc. 19, 197–231 (1968)

    MathSciNet  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Mechanics, State Key Laboratory of Fluid Power Transmission and Control, Zhejiang University, 310027, Hangzhou, People’s Republic of China

    Changshui Feng & Weiqiu Zhu

Authors
  1. Changshui Feng
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Weiqiu Zhu
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Weiqiu Zhu.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Feng, C., Zhu, W. Asymptotic Lyapunov stability with probability one of Duffing oscillator subject to time-delayed feedback control and bounded noise excitation. Acta Mech 208, 55–62 (2009). https://doi.org/10.1007/s00707-008-0126-3

Download citation

  • Received:

  • Revised:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00707-008-0126-3

Keywords

Search

Navigation