Introduction

Species have undergone important range contractions and expansions during the glacial and interglacial periods of the Pleistocene (Hewitt 1996). During the glaciations, the Central European lowlands were covered by steppe-tundra vegetation suitable for cold-adapted plant species, which were then widely distributed ('t Mannetje 2007). In the postglacial warming period, these species migrated to the cold, previously inhospitable alpine or arctic regions, but some remnant populations survived in lowland habitats with suitable conditions. A disjunct distribution in combination with a habitat type that had already existed during the glaciation is often considered to be an indicator for the glacial relict status of populations (Walter and Straka 1970). Cliffs are a typical habitat type that has existed and remained stable since glaciations, because it was hardly affected by forest recolonisation in the postglacial period or by human activity during the Holocene. Because cliffs are naturally rare and fragmented in lowland Europe, glacial relicts occurring on cliffs are suitable model species to study the effects of long-term fragmentation (Tang et al. 2010).

The effects of habitat fragmentation on the genetics of plant populations have been a topic of many recent studies (reviewed by Young et al. 1996; Leimu et al. 2006; Honnay and Jacquemyn 2007). Many rare species have been found to harbour less genetic diversity than more widespread species (compilation by Hamrick and Godt 1990; Cole 2003; Nybom 2004) due to the loss of alleles through random genetic drift (e.g. Young et al. 1996; Frankham and Wilcken 2006; Yuan et al. 2012). Furthermore, reduced gene flow among isolated populations in fragmented habitats has led to strong genetic differentiation between populations of many rare species (e.g. Fischer and Matthies 1998; Šmídová et al. 2011; Wagner et al. 2011). Loss of genetic variation and genetic differentiation is expected to increase with time since fragmentation (Coates 1988; Gitzendanner and Soltis 2000; Zawko et al. 2001). Thus, ice age relict populations that have been fragmented for a long time are expected to show strong genetic differentiation and low genetic diversity. Strong genetic differentiation has been reported for isolated alpine relict populations, such as Saxifraga cernua (Bauert et al. 1998), Erinus alpinus (Stehlik et al. 2002) and for the lowland remnant populations of Saxifraga paniculata (Reisch et al. 2003). However, not all studies have found low genetic diversity in ice age relicts (Lutz et al. 2000; Reisch et al. 2003), presumably due to the longevity of the species buffering random genetic drift. Genetic variation has profound implications for species conservation (Schaal et al. 1991; Ellstrand and Elam 1993; Ouborg et al. 2006) and assessing genetic variation within and between populations is essential for efficient conservation measures for rare species. Loss of genetic variability and increased inbreeding in small populations (Young et al. 1996; Frankham et al. 2002) may result in reduced fitness of offspring (Ellstrand and Elam 1993; Keller and Waller 2002). In the long term, reduced genetic variation may lower the evolutionary potential of a species in the face of changing environmental conditions, such as ongoing climate change.

Genetic variation is often assessed by studying the variability of neutral markers. However, adaptive loci that are responding to environmental variation may provide more relevant information on the potential of populations for rapid adaptation (Hoffmann and Willi 2008; Manel et al. 2012). Recently developed genome scan methods allow detecting candidate loci under selection on the assumption that natural selection is a locus-specific force, which increases the frequencies of locally beneficial alleles in a population (Strasburg et al. 2012). The distribution of these candidate loci among populations may then be compared with the distribution of environmental factors, such as temperature or precipitation that affect adaptive genetic variation.

We studied the genetic population structure and diversity of the endangered, long-lived plant Saxifraga rosacea Moench subsp. sponhemica (C.C. Gmel.) D.A. Webb, an endemic of Central Europe. Because of its disjunct distribution and habitat type (screes and cliffs), the species is considered to be an ice age relict (Thorn 1960; Walter and Straka 1970). We used RAPD-markers to address the following questions (1) How is genetic variation distributed among regions, populations and individuals? Does the genetic distance between populations increase with geographic distance? (2) Are populations of S. rosacea subsp. sponhemica characterised by low genetic diversity and does genetic diversity increase with population size? (3) Are there loci putatively under selection and is their frequency related to climatic variables?

Materials and methods

Species and study sites

Saxifraga rosacea subsp. sponhemica (hereafter called by its synonym S. sponhemica C.C. Gmel) is an evergreen perennial that grows either in compact cushions, formed by short and suberect shoots or as loose mats, formed by procumbent and rather long shoots (Tutin et al. 1968). Cushion size is highly variable (1–100 cm) and the number of rosettes per plant ranges from 1 to over 600. Individual rosettes are semelparous, but the genets are iteroparous. S. sponhemica is able to spread sexually via seeds and vegetatively via rosettes (pers. observation; Hemp 1996). Demographic data indicate that genets of S. sponhemica can live for several decades (Decanter, pers. comm.).

The flowers of S. sponhemica are strongly protandrous (Webb and Gornall 1989), but flowers ripen at different times within the same genet, which allows geitonogamous pollination. Common pollinators are Diptera (Muscidae and Syrphidae) and Apidae (Webb and Gornall 1989); we also observed some Coleoptera species as flower visitors. S. sponhemica has a mixed mating system with a selfing rate of about 46.8 % (Walisch unpubl.). S. sponhemica generally occurs on north to east facing rock faces, scree slopes and stone walls with no or little direct sunlight (Hemp 1996; pers. observation), which are fragmented habitats in lowland Europe. A few populations occur also on walls next to natural rock populations.

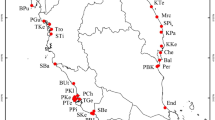
Saxifraga sponhemica has a disjunct distribution and occurs in the western part of its range in the Belgian Ardennes, the Luxembourg Oesling and the German Mid-Rhine region, with a few isolated populations in the French Jura, while in the east it occurs in the Bohemian low mountains (České středohoří) and in the Czech Bohemian Karst region (Českŷ kras), with isolated populations in the south of Moravia and in the Polish Sudetes (Webb and Gornall 1989; Fig. 1). The populations of S. sponhemica occur in regions that were not covered by glaciers during the last glaciation (Ehlers and Gibbard 2004), except for the populations in the French Jura. In most parts of its distribution area S. sponhemica is considered to be extremely rare or critically endangered and is legally protected (Korneck et al. 1996; Holub and Prochazka 2000; Colling 2005; Mirek et al. 2006).

Fig. 1
figure 1

Distribution (grey areas) of Saxifraga sponhemica (modified from Jalas and Suominen 1976). The sampling regions are marked as black dots on the map. In Luxembourg (LU) 13 populations were sampled, in Germany (DE) four, in Belgium (BE) five, in France (FR) two, and six in two regions of the Czech Republic: four in České středohoří (CZ-St), and two in Český kras (CZ-Kr)

Full size image

Sampling design

We studied 30 populations from six regions across the whole distributional range of S. sponhemica: the Ardennes, the Luxembourg Oesling, the German Mid-Rhine region, the French Jura, the České středohoří and the Českŷ kras (Fig. 1; Table 1). The geographic distances between the sampled populations within the six regions ranged from 0.1 to 14.9 km. To assess whether the studied populations formed a monophyletic group, we used ITS sequence data (ITS-1, 5.8 s and ITS-2) of three plants from each study population (Elvinger, pers. com.). We also included the sequence data from one specimen of the closely related subspecies S. rosacea subsp. rosacea. As an outgroup, we chose Saxifraga granulata. The results of a maximum likelihood tree analysis using version 3 of PhyML (Guindon and Gascuel 2003) with a GTR model of nucleotides substitution clearly indicated that all studied S. sponhemica populations formed a monophyletic group (Elvinger, pers. com.). Flow cytometry analysis of the DNA content indicated that all S. sponhemica populations had the same ploidy level (Elvinger, pers. com.).

Table 1 Genetic diversity of 30 populations of Saxifraga sponhemica
Full size table

In summer 2002 or 2003, we estimated the size of each population as the number of cushions (Table 1) and sampled 14 cushions along transects of 10–15 m length. Within each transect, we recorded the distances among the sampled plants. The minimum distance between two sampled plants was 100 cm to reduce the chance of sampling the same genetic individual repeatedly, but in populations consisting of less than 14 plants all accessible plants were sampled. In the six largest populations, we placed two transects to test for genetic structuring within the populations. Overall, 459 plants were sampled. Two fresh leaves were collected from each plant, placed in a small paper bag, and immediately frozen in liquid nitrogen. The samples were then stored at −80 °C.

RAPD-PCR

After grinding the frozen leaf material (Retsch MM200, Retsch, Haan, Germany), DNA was extracted using the DNeasy® Plant Mini Kit (QIAGEN, Germany). The DNA concentration of extracted DNA samples was determined by measuring their absorbance at 260 nm with a spectrophotometer (Biophotometer, Eppendorf, Hamburg, Germany). Amplifications were carried out in 25 μl volumes containing 5 μl of template DNA (5 ng DNA/μl); 8.575 μl ddH2O; 3 μl MgCl2 (25 mM); 0.5 μl dNTP’s (10 mM); 2.5 μl PCR buffer with (NH4)2SO4 (10×; Fermentas); 5 μl primer (5 μM); 0.3 μl Taq DNA polymerase (5 units/μl; Fermentas); and 0.125 μl BSA (20 mg/ml). The volumes were held in polycarbonate microtitre plates and covered by adhesive sealing sheets. The plates were then incubated in a thermocycler (iCycler®, Bio-Rad Laboratories) programmed with the following settings: denaturation of the DNA at 94 °C for 2 min, followed by 44 repetitive cycles consisting of denaturation for 45 s at 94 °C, annealing for 2 min 30 s at 36 °C, and extension for 2 min at 72 °C followed by a final extension phase of 5 min at 72 °C. The samples were kept at 4 °C until analysis. Amplified DNA fragments were separated by electrophoresis on precast ReadyAgarose™ 1.0 % agarose gels with ethidium bromide in 1× TBE buffer (Bio-Rad Laboratories) in an electrical field (85 V, c. 100 min). Gels were visualised under UV light and photographed using the Bio Doc system (Bio-Rad Laboratories).

In a first series of amplifications 40 10mer primers (Kits A, B from Operon Technologies, Alameda, CA) were screened in a random sequence and tested for reproducibility of the amplified fragment profile using four replicates of a single DNA extract. The first eight primers yielding good quality reproducible patterns (primers A5, A7, A9, A19, B7, B10, B17, and B18) were selected for the RAPD analysis of all 459 sampled plants (Table 2). Amplification products were scored visually for presence or absence of reliable bands using the program Quantity/One (Bio-Rad Laboratories) and were treated as phenotypes, with each band position representing a character either present or absent. The final presence–absence matrix contained scores at 61 polymorphic band positions for all samples in the study. We estimated the error rate of the RAPD genotyping by replicating 577 combinations of DNA samples and markers after DNA extraction resulting in 3,686 repeated banding scores (corresponding to 13.2 % of the total dataset). The second scoring was done by the same technician as the first one and the error rate was estimated to be 4.3 %.

Table 2 RAPD primers used
Full size table

For all genetic analyses, except for the analysis of between transect variation, we used 30 populations with only one transect per population. The RAPD fragment presence/absence matrix contained a total of 61 polymorphic loci and 380 plant samples. Because of the error rate of 4.3 %, we considered plants differing by less than four bands as putative clones belonging to the same genotype (Ehrich et al. 2008). Only one randomly chosen clone per genotype was kept in the RAPD fragment/absence matrix resulting in 352 samples used for further analysis.

Analysis of genetic diversity within populations

To estimate allele frequencies we used the Bayesian method with non-uniform prior distribution of allele frequencies (Zhivotovsky 1999) as implemented in AFLP-SURV version 1.0 (Vekemans 2002) with an estimate of Wright’s inbreeding coefficient over all populations (F IS). F IS was calculated using the Bayesian method implemented in HICKORY version 1.0.4 (Holsinger et al. 2002). Genetic diversity within populations was calculated as (1) the percentage of polymorphic loci (PPL) at the 5 % level, (2) Nei’s gene diversity (expected heterozygosity H eN) according to the method of Lynch and Milligan (1994) which uses the average expected heterozygosity of the marker loci.

Analysis of population structure

To infer population structure at the landscape level and assign individuals to the geographical regions we used the software STRUCTURE v. 2.3.4. which allows the use of dominant markers, such as RAPDs (Pritchard et al. 2000; Falush et al. 2003, 2007). We used the model of no admixture for the ancestry of the individuals without prior information of the regional membership of the populations and assumed that the allele frequencies are correlated among populations. We carried out a total of 300 runs (10 runs each for one to 30 clusters, i.e., K = 1–30) to quantify the amount of variation of the likelihood of each K. We found that a burn-in and Markov Chain Monte Carlo (MCMC) length of 105 each was sufficient as longer burn-ins or MCMC lengths did not change significantly the results. In STRUCTURE, the model choice criterion to detect the K most appropriate to describe the data is given as ‘Ln P(D)’ which is an estimate of the posterior probability of the data given K. The maximum value of Ln P(D) returned by STRUCTURE, to which we refer as L(K) afterwards, is often taken as the true value of K. However, the distribution of L(K) does often not show a clear mode for the number of groups. We used an ad hoc quantity based on the second-order rate of change of the likelihood function (∆K) with respect to K (Evanno et al. 2005) as implemented in STRUCTURE HARVESTER (Earl and von Holdt 2012). It is calculated as ∆K = m(|L(K + 1) − 2L(K) + L(K − 1)|)/sd[L(K)] where m is the mean and sd the standard deviation. The height of this modal value was used as an indicator of the signal detected by STRUCTURE to find the highest modal value. Finally, the ten runs of the simulation with the highest modal value of ∆K were aligned using the FullSearch option in CLUMPP (cluster matching and permutation program; Jakobsson and Rosenberg 2007). Convergence of the 10 replicate runs for K = 3 was high as they produced very similar clustering results as shown by the pairwise G’ (similarity function) values (>0.99) for each pair of permutated runs in CLUMPP. The mean membership coefficients were represented as a bar graph using DISTRUCT (Rosenberg 2004).

The genetic structure within and among populations was first analysed using the Bayesian method suggested by Holsinger et al. (2002) as implemented in HICKORY (version 1.0.4; Holsinger and Lewis 2006). This method allows a direct estimate of the overall F ST from dominant markers without assuming previous knowledge of the inbreeding coefficient within populations and Hardy–Weinberg equilibrium. We used HICKORY with a full model and using non-informative priors for f (estimate of F IS) and θ B (estimate of F ST). To ensure that the results were consistent we conducted several runs with default sampling parameters (burn-in = 50,000, sample = 250,000, thin = 50). The method also allowed inference of the within-population inbreeding coefficient F IS.

The genetic structure within and among populations was also analysed on the basis of RAPD allele frequencies with AFLP-SURV assuming the inbreeding coefficient calculated by HICKORY. We used 1,000 permutations to assess the significance of the calculated F ST. A pairwise genetic distance matrix with F ST values was calculated in AFLP-SURV assuming the inbreeding coefficient estimated by HICKORY and used as input for a principal coordinate analysis (PCoA). The partitioning of genetic variation among the clusters identified by STRUCTURE, geographical regions within these clusters, populations within regions, and among individuals within populations was investigated by analysis of molecular variance (AMOVA) using the R-package ade4 (Dray and Dufour 2007).

To test for isolation by distance, we applied Mantel test statistics correlating the pairwise F ST values and the geographic distance matrix using GenAlex 6.501 (Peakall and Smouse 2006, 2012). Significance levels were obtained after performing 999 random permutations for the Mantel test.

High genetic differentiation is not always a consequence of low gene flow, but can also result from a migration–drift disequilibrium when drift plays an important role, such as in small populations (Whitlock and McCauley 1999). We estimated the population-specific F ST values using BAYESCAN 2.01 (Foll and Gaggiotti 2008) with the default settings and used linear regressions to test if there was a relationship between the population-specific F ST values and measures of genetic diversity (PPL and H eN) of populations. We expect a strong relationship if genetic differentiation is strongly affected by genetic drift (both current and historical), reflecting a migration–drift disequilibrium. If on the other hand populations are in migration–drift equilibrium, no such relationship is expected (Cox et al. 2011).

Not all molecular markers are necessarily selectively neutral. We identified markers under divergent or balancing selection with the program BAYESCAN 2.01 with the false discovery rate set to 0.05 (see Foll and Gaggiotti 2008). Several methods of detecting markers under selection have recently been tested by De Mita et al. (2013). The method used by BAYESCAN 2.01 was found to be robust against deviations from the island model and yielded very few false positives in all simulations. To analyse if there is a relationship between putative non-neutral markers and climatic conditions, we obtained the following bioclimatic variables for each study site for the current conditions (interpolations of observed climate data, representative of 1950–2000) in a grid size of about one square kilometre (30 arc seconds) from the WORLDCLIM database version 1.4. (Hijmans et al. 2005): mean annual temperature, temperature seasonality, maximum temperature, minimum temperature, and annual precipitation. We reduced the climatic variables to two principle components using principle component analysis with varimax rotation. We then studied the relationship between the identified non-neutral markers and the two principal components by multiple logistic regressions, using the GLM package of R (version 3.0.1, R Core team 2013). Finally, we removed the loci identified as non-neutral from the dataset and ran a second AMOVA to compare it with the AMOVA based on the complete dataset.

Genetic structure within populations and clonal structure

The genetic structure within populations was studied by autocorrelation analyses using an estimator of the kinship coefficient for dominant markers, F ij (Hardy 2003) as implemented in SPAGeDI version 1.2. (Hardy and Vekemans 2002). This method does not assume Hardy–Weinberg genotypic proportions, but requires an estimate of the departure from these conditions (i.e., that the inbreeding coefficient is known). We used the HICKORY estimate of F IS. The kinship coefficient, F ij is defined as the probability that a random gene from individual i is identical to a random gene from individual j. To visualize and describe the spatial genetic structure (SGS) within populations of S. sponhemica, mean F ij estimates over pairs of individuals at a given distance interval r, F(r), were plotted against distance in a spatial autocorrelogram. If F(r) tends to decrease linearly with r or ln (r), the extent of SGS can be quantified by the slope (b) of a regression of mean F ij estimates on r ij or ln (r ij ). As (b) can depend on the sampling scheme used, we calculated the ratio −b/(1 − F (1)) where F (1) is the mean F ij between individuals belonging to the first distance class. F (1) can be considered as an approximation of the kinship coefficient between neighbouring individuals if the first distance class contains enough pairs of individuals. The ratio –b/(1 − F (1)) is referred to as the Sp statistic (Vekemans and Hardy 2004) and can be used to compare the extent of SGS among populations or species. Standard errors for the mean F ij estimates over pairs of individuals at a given distance interval and the regression slope (b) were assessed by a jack knifing procedure over loci. The significance level of the regression slope (b) was evaluated by comparing the observed value with the distribution of (b) obtained by 1,000 random permutations.

Results

Genetic diversity within populations

The eight RAPD primers used for analysis generated a total of 61 polymorphic bands. No private (population-specific) bands were observed. Taking into account an error rate of 4.3 %, individuals differing by up to 2.6 (rounded to 3) loci were considered as possible ramets belonging to the same clonal lineage. This resulted in 23 putative clones and 352 unique genotypes. The mean proportion of polymorphic loci (PPL) in the 30 populations was 83.8 % and varied among the populations from 47.5 to 96.7 % (Table 1). PPL was much lower in the French Jura populations than in those from Luxembourg or Germany (67 vs. 89 %, P < 0.05; Tukey’s test). Overall, mean Nei’s gene diversity (H eN) within populations using the F IS estimated by HICKORY was 0.265, and like PPL it was particularly low in the populations from the French Jura and high in those from Luxembourg and Germany, but this difference was only marginally significant (P = 0.058). None of the gene diversity measures increased significantly with population size (r < 0.29, P > 0.12).

Population structure

Using the modal value of ∆K rather than the maximum value of L(K) allowed us to identify with STRUCTURE several groups corresponding to the uppermost hierarchical level of partitioning among populations (Fig. 2). The highest modal value of ∆K was at K = 3. The first cluster identified by STRUCTURE consisted of three regions (LU, DE and FR), while the other two clusters corresponded to the Belgian (BE) and Czech regions (CZ-St and CZ-Kr) (Fig. 3).

Fig. 2
figure 2

Results of a STRUCTURE analysis (10 runs each for K = 1–30) to infer the population structure of Saxifraga sponhemica at the landscape level; ∆K is plotted as a function of K. The highest modal value of ∆K is at K = 3 corresponding to the number of geographical regions (see text for details)

Full size image
Fig. 3
figure 3

Estimated population structure of Saxifraga sponhemica inferred by a Markov chain Monte Carlo Bayesian clustering method (STRUCTURE version 2.2) of RAPD data. Each individual is represented by a vertical line, which is partitioned into a maximum of K = 3 differently shaded segments that represent the individual’s estimated membership fractions in three clusters. Vertical black lines separate the 32 populations. Runs of ten simulations were aligned using CLUMPP (see text for details). For population codes, see Table 1

Full size image

The PCoA analysis based on pairwise F ST distances revealed a clustering pattern very similar to the clusters identified by STRUCTURE (Fig. 4). Populations from the Czech Republic and Belgium formed two distinct clusters whereas the remaining populations formed one large cluster. The PCoA analyses thus confirmed that populations from Luxembourg, Germany and France are closely related.

Fig. 4
figure 4

PCoA analysis based on F st genetic distances derived from RAPD markers of 30 populations of Saxifraga sponhemica. Ovals correspond to the three clusters identified by a STRUCTURE analysis. The symbols denote six geographical regions: filled circles Ardennes (BE), unfilled circles Oesling (LU), filled squares Mid-Rhine (DE), filled triangles Jura (FR), dark filled inverted triangles České středohoří (CZ), light filled inverted triangles Český kras (CZ)

Full size image

The posterior mean Bayesian estimate in the HICKORY analysis for F IS (f) was 0.314 ± 0.124 (95 % credible interval 0.085–0.562) suggesting a moderate amount of inbreeding within populations. Estimates of F IS based on HICKORY analysis of dominant markers have to be regarded with caution, but are plausible if consistent with estimates based on other information (Holsinger and Lewis 2006). Our HICKORY estimate of F IS (f) was very similar to an estimate of F IS = 0.305 computed as F IS = s/(2 − s) (Hartl and Clark 1997) with a self-fertilisation rate (s) of 0.468. The self-fertilisation rate was estimated in a pollination experiment in a large population in Luxembourg (Walisch et al. unpublished). Furthermore, our study was based on a relatively large number of populations and loci suggesting that our inferences about F IS with HICKORY are plausible (Holsinger et al. 2002).

In the Bayesian analysis of population structure with HICKORY, the posterior mean estimate of F ST (θ B ) was slightly higher than the traditional estimate of F ST estimated by AFLP-SURV assuming the HICKORY estimate of F IS = 0.314 (F ST = 0.3836 ± 0.0032 and F ST = 0.3369 ± 0.0075, respectively). The AMOVA estimate (Φ ST = 0.377) was similar to the HICKORY estimate. The AMOVA analysis showed that there was significant genetic differentiation among the three clusters identified by STRUCTURE, the six geographical regions within the clusters, and among populations within regions (Table 3). Overall, more than 16 % of the variation was among regions. An AMOVA based only on the populations with two transects showed that the variation among transects within populations accounted for 12 % of the total genetic variation, while variation among individuals within transects accounted for another 57 %.

Table 3 Partitioning of the genetic variation of Saxifraga sponhemica by AMOVA among three genetic clusters as identified by STRUCTURE, six geographical regions within these clusters [Oesling (LU), Mid-Rhine (DE), Jura (FR), Ardennes (BE), České středohoří (CZ), and Český kras (CZ)], populations within regions, and individuals within populations
Full size table

Genetic differentiation among the populations (pairwise F st) increased with geographic distance (Fig. 5a), indicating an isolation by distance (IBD) pattern among the populations. At the regional level, we detected IBD in the western cluster, among the Luxembourg and German populations (r = 0.49, P < 0.001, Fig. 5b), but not in the eastern cluster, among the Czech populations (r = 0.22, P = 0.20). However, because of the lower number of populations in the east, the statistical power to detect IBD in the east was much lower than in the west.

Fig. 5
figure 5

The relationship between genetic distances (pairwise F st) and geographic distances for a 28 sampled populations of Saxifraga sponhemica (all populations except for BE25 and FR29 with only two samples), and for b a subset consisting of the populations from Luxembourg and Germany. P values were derived from Mantel tests. Note log scales for geographic distances

Full size image

Nei’s gene diversity of a population strongly decreased with its specific F ST value (Fig. 6; r = −0.85, P < 0.0001), and the proportion of polymorphic loci less strongly (r s = −0.39, P < 0.05), indicating that populations were not in migration–drift equilibrium. The populations BE25 and FR29 (Table 1) which consisted of only two individuals were omitted from this analysis. Using the program BAYESCAN 2.01 (Foll and Gaggiotti 2008), nine loci (15 % of all loci) were identified as outliers and were considered to be putatively under selection or linked to loci under selection. Divergence of five loci (8 %) was higher and that of four (7 %) significantly lower than under a neutral expectation indicating that directional selection may be occurring at similar frequency as balancing selection. We identified two principal components (PCs) by PCA with varimax rotation on climate variables. PC1 explained 67 % of the variation and was mainly correlated with temperature seasonality (r = −0.94), minimum temperature (r = 0.83) and annual precipitation (r = 0.82), indicating that PC1 represented decreasing continentality. PC2 explained a further 22 % of the variation and was highly correlated with maximum temperature (r = 0.98). Multiple logistic regressions indicated that the frequency of four of the five putative loci under diversifying selection were related to either one or both of the continentality and temperature gradients (Table 4). An AMOVA of a reduced data set without the putatively non-neutral molecular markers resulted in a slightly lower Φ ST value than the AMOVA based on the whole dataset (Φ ST = 0.355 vs. 0.377, respectively).

Fig. 6
figure 6

Relation between gene diversity (H eN) and the population specific F st values in Saxifraga sponhemica. The populations (BE25, FR29) with only two samples were excluded from the analysis

Full size image
Table 4 Intercepts and regression coefficients from multiple logistic regression analyses of the relationship between the frequency of four loci putatively under diversifying selection in populations of Saxifraga sponhemica and two principal components describing bioclimatic gradients (continentality and maximum temperature) among the sites
Full size table

Spatial genetic structure within populations

Spatial autocorrelation analysis within populations based on observations across all populations revealed a significant spatial genetic structure within populations of S. sponhemica in agreement with an isolation by distance model (Fig. 7). Mean kinship coefficients decreased with distance between plants in the populations (b = −0.039, P < 0.001), indicating that individual plants growing close together had a higher probability to be genetically related than plants separated by larger distances. Positive values of the mean kinship coefficient were obtained at small geographical distances (<1.5 m), suggesting that neighbouring individuals are genetically more closely related than random pairs of individuals within the populations (Fig. 7). The value for the Sp statistic was 0.041 with F (1) = 0.030.

Fig. 7
figure 7

Mean kinship coefficient between pairs of individuals in 30 populations of Saxifraga sponhemica that grow at different distances from each other assessed using 61 RAPD markers. Each of the 15 distance classes involves 202–205 pairs of individuals and the total sample consisted of 352 individuals. Means ± 1 SE. The open symbols represent significant mean kinship coefficients (P < 0.05)

Full size image

The analysis of RAPD phenotypes differing by up to three bands (4.3 % error rate) revealed that 13.7 % of samples were part of 23 putative clonal lineages. Each putative clone was restricted to a single transect. The distance between members of the same putative clone ranged from 0.15 to 6.95 m.

Discussion

Population genetic structure

We found in S. sponhemica a strong correlation between genetic and geographical distance, indicating an isolation by distance (IBD) pattern due to gene flow among geographically close populations. However, the current gene flow between most of the populations is very low or absent, because the current distribution is highly disjunct, most extant populations are strongly isolated from each other, and the seeds have no special adaptations for long-range dispersal. The observed pattern of IBD may thus reflect historical gene flow, probably dating back to the last glaciation when suitable open habitats for S. sponhemica like screes and rock cliffs were much more abundant ('t Mannetje 2007) and the species was likely to be more common. After the immigration and spread of trees, the populations of S. sponhemica would have been restricted to the few remaining open, treeless habitats and been strongly fragmented. A likely explanation for the preservation of the historical genetic pattern is the longevity and clonality of S. sponhemica, which slows down genetic drift (Aguilar et al. 2008). Other studies of long-lived ice age relicts, such as S. paniculata (Reisch et al. 2003) and Dodecatheon amethystinum (Oberle and Schaal 2011) have also found IBD among populations that are today strongly isolated.

The results of the STRUCTURE and PCoA analyses suggest that the genetic population structure of S. sponhemica is hierarchical and consists of three clusters substructured into several populations. The identified genetic groups were, however, not completely concordant with the geographic regions. The distinctness of the populations in the Belgian Ardennes, despite their close proximity to the populations in Luxembourg and Germany suggests that the Belgian populations have been separated for a longer time. The Φ ST value of 0.377 found for S. sponhemica is comparable to the average Φ ST values found in a review of a large number of studies that have used dominant molecular markers (RAPDs and AFLPs) to study genetic differentiation in plants (0.34 and 0.35, respectively) and to the mean for other plants with a mixed mating system (0.40; Nybom 2004). The strong genetic differentiation even between S. sponhemica populations that are only a few kilometre from each other indicate low gene flow due to restricted pollinator movement and very limited seed dispersal (Ægisdóttir et al. 2009; Colling et al. 2010) between the cliff and scree habitat patches although the seeds of S. sponhemica are very small. This is supported by the significant differentiation between subpopulations (transects) within populations.

Loci under natural selection

Most studies on population genetic structure using molecular genetic markers have assumed that these markers are selectively neutral. However, recent genome scan studies showed that a significant amount of among population variation can be due to selection (Strasburg et al. 2012; Manel et al. 2012). In S. sponhemica, we found that 15 % of the studied RAPD markers could be considered to be non-neutral outliers, which may be linked to loci under directional or balancing selection, a proportion similar to that found in other genome scan studies (0.4–35.5 %, Strasburg et al. 2012; 10 %, Manel et al. 2012). Variability in four of the loci putatively under selection showed a strong association with climatic gradients, suggesting adaptive genetic variation in response to climate. Climatic factors are strong selective forces and a number of studies have found that genetic variation among natural populations was related to climatic gradients (e.g., Jump et al. 2006; Richardson et al. 2009; Poncet et al. 2010; Cox et al. 2011; Manel et al. 2012). Adaptive genetic variation is important for the potential of a species to adapt to environmental changes, such as ongoing climate change (Hoffmann and Willi 2008; Manel et al. 2012), provided that favourable alleles can spread. However, gene flow is very unlikely among the widely disjunct regions in which S. sponhemica occurs.

Within population genetic structure

We found a significant spatial genetic structure within subpopulations at small distances, indicating restricted gene flow in agreement with an isolation by distance model. The Sp value of 0.041 (with F (1) = 0.030) over all loci was similar to the mean for species with a mixed mating system (0.037; Vekemans and Hardy 2004). Positive mean kinship values indicated that neighbouring individuals (<1.5 m) were genetically more closely related than random pairs of individuals. This could be due to the mixed mating system of S. sponhemica that allows geitonogamy, in combination with restricted pollen and seed dispersal. In the sampled S. sponhemica populations, putative clones occurred at a low proportion (13.7 %), but over considerable distances (up to 7 m) through the detachment of rosettes.

Genetic diversity within populations

Many studies have found that the genetic variability of populations of rare plants is lower than that of common species (see Gitzendanner and Soltis 2000; Cole 2003; Nybom 2004; references therein), a pattern that was also found in a comparison of 14 rare and common species of the Saxifragaceae (Soltis and Soltis 1991). This has been attributed to genetic drift in the often small and isolated populations of rare plants. In contrast, despite their long isolation, the overall genetic diversity of populations of S. sponhemica was similar to that found in other species with a mixed mating system (Nybom 2004). Similarly, other central European ice age relicts, such as S. paniculata (Reisch et al. 2003), and S. aizoides (Lutz et al. 2000), that occur on rocks have also maintained high genetic diversity despite a fragmented distribution. The maintenance of genetic diversity of these plants is probably due to their longevity and the long-term stability of their habitats (Young et al. 1996; Tang et al. 2010). High gene diversity, combined with moderate to high genetic differentiation and IBD has been found in a number of other cliff species, such as Centaurea wiedemanniana (Sözen and Özaydin 2010), D. amethystinum (Oberle and Schaal 2011), Dracocephalum austriacum (Dostálek et al. 2010), and Taihingia rupestris (Tang et al. 2010).

Many studies have found a relationship between the size of the populations and their genetic diversity (Leimu et al. 2006), because small populations have lost variation through genetic drift. In contrast, the genetic diversity of small S. sponhemica populations was comparable to that of larger populations. Strong reductions in genetic variability have been found in small populations of plants with a shorter generation time (Fischer and Matthies 1997; Aguilar et al. 2008). The longevity and the long-term stability of habitats of S. sponhemica might have buffered the effects of drift on genetic diversity. However, the strong relationship between genetic diversity and population specific F st values (Fig. 5) indicating a strong gene flow drift disequilibrium suggests that genetic drift has modified the population genetic structure of S. sponhemica since the postglacial isolation of the remnant populations due to forest recolonisation. The particularly low proportion of polymorphic loci in the French Jura populations could be due to founder effects during postglacial warming, because these populations are situated in valleys that had been covered by ice during the last glaciation (Bichet and Campy 2008).

Conclusions

Our results suggest that long-lived plant species like S. sponhemica can maintain historic genetic patterns despite mostly small population sizes and strong isolation. Today, the distribution of S. sponhemica is disjunct, consisting of groups of populations that have been strongly isolated from each other for a long time by the spread of trees after the ice age. The extant populations are even at a small geographical scale genetically differentiated, indicating low current gene flow. However, populations still show an isolation by distance pattern, suggesting that the underlying population genetic patterns in S. sponhemica were shaped by historical gene flow among interconnected populations during the last ice age.

Fragmentation of populations can result in genetic erosion, i.e., loss of genetic diversity and increased inbreeding (Young et al. 1996; Ouborg et al. 2006) which in turn may result in reduced fitness of plants (Ouborg et al. 1991; Fischer and Matthies 1998; Reed and Frankham 2003). In S. sponhemica, considerable genetic variability has been preserved in most populations. We identified several non-neutral markers whose occurrence correlated with climatic gradients, indicating that there is genetic differentiation among populations in traits under selection.

Saxifraga sponhemica is a rare Central European endemic species with few extant populations. Although the habitats of the species are stable and most populations do not appear to be threatened in the short term, extinction of populations due to habitat destruction has been observed (Walisch unpubl.). The small number of populations thus presents a threat to the overall survival of the species. The creation of new populations in suitable habitats within the different regions might thus be considered. Because of the significant clines in non-neutral markers, seeds from the same region should be used to avoid potential maladaptation to local conditions (Becker et al. 2006, 2008).