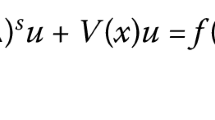Skip to main content
SpringerLink
Log in

The existence of mild and classical solutions for time fractional Fokker–Planck equations

  • Published:
Monatshefte für Mathematik Aims and scope Submit manuscript

Abstract

Time fractional Fokker–Planck equations can be used to describe the subdiffusion in an external time-and space-dependent force field F(t, x). In this paper, we convert it to the form of the following problems

$$\begin{aligned}\partial _tu-\kappa _\alpha \partial _t^{1-\alpha }\Delta u=\nabla \cdot (F\partial _t^{1-\alpha }u)+f,\end{aligned}$$

where \(\alpha \in (0,1)\). We obtain some results on existence and uniqueness of mild solutions allowing the “working space" that may have low regularity. Secondly, we analyze the relationship between “working space" and the value range of \(\alpha \) when investigating the problem of classical solutions. Finally, by constructing a suitable weighted Hölder continuous function space, the existence of classical solutions is derived without the restriction on \(\alpha \in \left( \frac{1}{2},1\right) \).

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Barkai, E., Metzler, R., Klafter, J.: From continuous time random walks to the fractional Fokker-Planck equation. Phys. Rev. E 61, 132–138 (2000)

    Article  MathSciNet  Google Scholar 

  2. Beckers, S., Yamamoto, M.: Regularity and unique existence of solution to linear diffusion equation with multiple time-fractional derivatives. In: Bredies, K., Clason, C., Kunisch, K., von Winckel, G. (eds.) Control and Optimization with PDE Constraints, pp. 45–56. Birkhäuser, Basel (2013)

  3. Eidelman, S.D., Kochubei, A.N.: Cauchy problem for fractional diffusion equations. J. Differ. Equ. 199, 211–255 (2004)

    Article  MathSciNet  Google Scholar 

  4. Fujiwara, D.: Concrete characterization of the domains of fractional powers of some elliptic differential operators of the second order. Proc. Jpn. Acad. 43(2), 82–86 (1967)

    MathSciNet  MATH  Google Scholar 

  5. Henry, B.I., Langlands, T.A.M., Straka, P.: Fractional Fokker-Planck equations for subdiffusion with space- and time-dependent forces. Phys. Rev. Lett. 105, 170602 (2010)

    Article  Google Scholar 

  6. Henry, D.: Geometric Theory of Semilinear Parabolic Equations. Lecture Notes in Math, vol. 840. Springer-Verlag, New York/Berlin (1981)

  7. Herrmann, R.: Fractional Calculus: An Introduction for Physicists. World Scientific, Singapore (2011)

    Book  Google Scholar 

  8. Hilfer, R.: Applications of Fractional Calculus in Physics. World Scientific, Singapore (2000)

    Book  Google Scholar 

  9. Huang, C., Le, K.N., Stynes, M.: A new analysis of a numerical method for the time-fractional Fokker-Planck equation with general forcing. IMA J. Numer. Anal. (2019) (to appear). https://doi.org/10.1093/imanum/drz006

  10. Kemppainen, J., Siljander, J., Zacher, R.: Representation of solutions and large- time behavior for fully nonlocal diffusion equations. J. Differ. Equ. 263(1), 149–201 (2017)

    Article  MathSciNet  Google Scholar 

  11. Kemppainen, J., Siljander, J., Vergara, V., Zacher, R.: Decay estimates for time-fractional and other non-local in time subdiffusion equations in \({\mathbb{R}}^d\). Mathematische Annalen 1–39 (2014)

  12. Kilbas, A.A., Srivastava, H.M., Trujillo, J.J.: Theory and Applications of Fractional Differential Equations, North-Holland Math. Stud., vol. 204. Elsevier Science B.V., Amsterdam (2006)

  13. Kubica, A., Yamamoto, M.: Initial-boundary value problems for fractional diffusion equations with time-dependent coefficients. Fract. Calc. Appl. Anal. 21(2), 276–311 (2018)

    Article  MathSciNet  Google Scholar 

  14. Le, K.N., McLean, W., Stynes, M.: Existence, uniqueness and regularity of the solution of the time-fractional Fokker-Planck equation with general forcing. Commun. Pure Appl. Anal. 18(5), 2789–2811 (2019)

    Article  MathSciNet  Google Scholar 

  15. Le, K.N., McLean, W., Mustapha, K.: Numerical solution of the time-fractional Fokker-Planck equation with general forcing. SIAM J. Numer. Anal. 54, 1763–1784 (2016)

    Article  MathSciNet  Google Scholar 

  16. Le, K.N., McLean, W., Stynes, M.: Existence, uniqueness and regularity of the solution of the time-fractional Fokker-Planck equation with general forcing. Commun. Pure Appl. Anal. 18(5), 2765–2787 (2019)

    Article  MathSciNet  Google Scholar 

  17. Li, L., Liu, J.G., Wang, L.: Cauchy problems for Keller-Segel type time-space fractional diffusion equation. J. Differ. Equ. 265(3), 1044–1096 (2018)

    Article  MathSciNet  Google Scholar 

  18. Luchko, Y.: Initial-boundary-value problems for the generalized multi-term time-fractional diffusion equation. J. Math. Anal. Appl. 374, 538–548 (2011)

    Article  MathSciNet  Google Scholar 

  19. McLean, W., Mustapha, K., Ali, R., Knio, O.: Well-posedness of time-fractional advection-diffusion-reaction equations. Fract. Calc. Appl. Anal. 22(4), 918–944 (2019)

    Article  MathSciNet  Google Scholar 

  20. McLean, W., Mustapha, K., Ali, R., Knio, O.: Regularity theory for time-fractional advection-diffusion-reaction equations. Comput. Math. Appl. 79(4), 947–961 (2020)

    Article  MathSciNet  Google Scholar 

  21. Metzler, R., Barkai, E., Klafter, J.: Deriving fractional Fokker-Planck equations from a generalised master equation. Europhys. Lett. 46, 431–436 (1999)

    Article  MathSciNet  Google Scholar 

  22. Metzler, R., Barkai, E., Klafter, J.: Anomalous diffusion and relaxation close to thermal equilibrium: a fractional Fokker-Planck equation approach. Phys. Rev. Lett. 82, 3563–3567 (1999)

    Article  Google Scholar 

  23. Podlubny, I.: Fractional Differential Equations. Academic Press, San Diego (1999)

    MATH  Google Scholar 

  24. Sakamoto, K., Yamamoto, M.: Initial-value-boundary-value problems for fractional diffusion-wave equations and applications to some inverse problems. J. Math. Anal. Appl. 382(1), 426–447 (2011)

    Article  MathSciNet  Google Scholar 

  25. Zhang, Q.G., Sun, H.R.: The blow-up and global existence of solutions of Cauchy problems for a time fractional diffusion equation. Topol. Methods Nonlinear Anal. 46(1), 69–92 (2015)

    Article  MathSciNet  Google Scholar 

  26. Zhou, Yong: Infinite interval problems for fractional evolution equations. Mathematics 10, 900 (2022)

    Article  Google Scholar 

  27. Zhou, Y., He, J.W., Ahmad, B., Tuan, N.H.: Existence and regularity results of a backward problem for fractional diffusion equations. Math. Meth. Appl. Sci. 42, 6775–6790 (2019)

    Article  MathSciNet  Google Scholar 

  28. Zhou, Y., He, J.W.: Well-posedness and regularity for fractional damped wave equations. Monatshefte für Mathematik 194(2), 425–458 (2021)

    Article  MathSciNet  Google Scholar 

Download references

Acknowledgements

Project supported by National Natural Science Foundation of China (12001462, 12071396) and the General Project of Hunan Provincial Education Department of China (21C0083).

Author information

Authors and Affiliations

  1. Faculty of Mathematics and Computational Science, Xiangtan University, Hunan, 411105, China

    Li Peng & Yong Zhou

  2. Faculty of Information Technology, Macau University of Science and Technology, Macao, 999078, China

    Yong Zhou

  3. National Center for Applied Mathematics, Hunan, China

    Li Peng

Authors
  1. Li Peng
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Yong Zhou
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Yong Zhou.

Additional information

Communicated by Ansgar Jüngel.

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Peng, L., Zhou, Y. The existence of mild and classical solutions for time fractional Fokker–Planck equations. Monatsh Math 199, 377–410 (2022). https://doi.org/10.1007/s00605-022-01710-4

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00605-022-01710-4

Keywords

Mathematics Subject Classification

Search

Navigation