1 Introduction

Characterization of fractured rock mass is a critical task in the development of open-pit and underground mining for the design of slopes, support means or blast optimization. Discrete Fracture Networks (DFNs) have proved to be an effective tool for the three-dimensional representation of a natural fracture network (Baecher et al. 1977; Long et al. 1982; Baecher 1983; Andersson et al. 1984; Dershowitz and Einstein 1988; Zhang et al. 2002; Miyoshi et al. 2018) and are increasingly being used in many geotechnical and mining engineering problems (Elmo et al. 2015; Elmouttie and Poropat 2012; Umili et al. 2020) e.g., in analysis of rock slope stability (Bonilla-Sierra et al. 2015), geo-mechanical and hydrological behavior of fractured rocks (Robinson 1983; Andersson et al. 1984; Lei et al. 2017), seismic attenuation and stiffness modulus dispersion Hunziker et al. (2018), and multi-physics processes, see e.g., Keilegavlen et al. (2021).

The basis of the DFN method is the characterization of fracture parameters using statistical analysis to build a computational model that explicitly represents the geometrical properties of each individual discontinuity and the topological relationships between individual discontinuities and discontinuity sets (Lei et al. 2017; Miyoshi et al. 2018). In general, the term ‘discontinuity’ groups all weak planes of geological origin, such as fractures, joints, bedding planes, cleavages and faults (Lu 1997). In what follows we are treating all these terms equivalently. Among the geometrical properties of each fracture, one may emphasize orientation, size, location, shape and aperture and their corresponding probability distributions (Baecher et al. 1977; ISRM 1978; Baecher 1983; Dershowitz and Einstein 1988; Dershowitz and Herda 1992). Other relevant characteristics may also be considered, such as genetic type, filling material (Hekmatnejad et al. 2018) and roughness (Tang et al. 2022 and Zou et al. 2022).

Traditionally, DFN models group visible fractures by orientation in families of poles (ISRM 1978) on the stereographic projection. This is done by dividing the stereogram into sectors and fitting directional probability distributions. The most frequent are the bivariate von Mises–Fisher and Bingham (Bingham 1964; Baecher 1983; Fisher et al. 1993). The goodness of the fit is assessed using the chi-squared and the Kolmogorov–Smirnov tests (Baecher 1983). Similarly, analytical probability density functions (pdfs), such as lognormal, uniform, power law, gamma, normal, etc., are used to characterize the distribution of trace lengths measured on an outcrop (Tonon and Chen 2007). Even though analytical forms seldom provide satisfactory approximations to orientation data (Baecher 1983), works in which the statistical analysis is performed in a non-parametric way are rare, see e.g., Xu and Dowd (2010), and those that treat jointly the disk orientation and size pdfs in a non-parametric way are non-existent, to the authors’ knowledge. In this work, we use directional-linear statistics as a way to jointly estimate the density functions of fracture sizes and orientations, based on the theory of directional-linear kernels by García-Portugués et al. (2013). In directional statistics, the sample space is the unit sphere, while in directional-linear statistics, the sample space is the Cartesian product of a sphere and the real line.

Because the rock mass structure is impossible to be directly observed without dismantling it completely (Priest 1993), a variety of methods must be used for sampling discontinuity data. From that observation, the ‘true’ joint density function of orientation-sizes inherent to the rock mass is inferred through stereology. Data from exposed rock faces, such as natural outcrops, excavation faces, and boreholes have proved to be useful (Tonon and Chen 2007). Among sampling techniques for deriving fracture parameters, the most utilized are in-hole images or wireline geophysical logging (Ozkaya aand Mattner 2003; Hekmatnejad et al. 2019), scanline survey, circle sampling or window survey (Priest and Hudson 1981a, b; Kulatilake et al. 2003; Kulatilake and Wu 1984; Zhang and Einstein 1998, 2000; Song and Lee 2001; Jimenez-Rodriguez and Sitar 2006), as well as digital photogrammetry and laser scanning techniques (Elmo et al. 2015; Vollgger and Cruden 2016).

The history of the problem of determining density functions of disk sizes from trace length probability density functions is well summarized by Tonon and Chen (2007). The work of Warburton (1980b) provided a starting point for estimating trace length probability density functions from disk size density functions, using stereological principles, for disks without aperture, circular in shape, parallel to each other and with centers arranged within a volume following a Poisson process, see e.g., Baecher et al. (1977). Other contributions assume fractures to be elliptical in shape (Zhang et al. 2002) (Guo et al. 2022 and Zheng et al. 2022). The inverse process, i.e., obtaining disk sizes pdf from trace lengths, was already formulated years before by Santaló (1955). However, works by Tonon and Chen (2007, 2010) showed that this relationship leads in some cases to non-positive pdf values; it also fails for bimodal or multimodal distributions. As this type of distributions is common in the field, a solution to this problem is explored in this work using one of the Bertrand’s paradoxes (Bertrand 1888; Aldous et al. 1988; Chiu and Larson 2009) and its relation with Warburton’s work (Warburton 1980a).

When characterizing rock exposures, one should consider bias effects inherent to the sampling procedure. According to Kulatilake and Wu (1984), Priest and Hudson (1981a, b), Laslett (1982), Baecher and Lanney (1978), Baecher (1983), Villaescusa and Brown (1992) and Chilès and Marsily (1993) there are four main causes of bias in the distribution of trace lengths: censoring, truncation, size and relative orientation. Censoring occurs when one or both terminations of a trace are not observable. This effect occurs when the surveying surface is finite; the disk orientation-size density function and the size, shape and orientation of the surface to be intersected have also some influence. The resulting traces may be grouped into three categories according to the number of terminations or censoring condition, namely complete, semi-bounded and bounded (White and Willis 2000). Truncation is introduced because traces shorter than a cut-off length (Baecher 1983) cannot be observed. When an observer maps traces on an outcrop, unintentional truncation occurs. Operator’s skills, and sampling scale, makes that small traces are less likely to be observed. That is what Riley (2005) called ‘the protocol adopted for recording short traces (lower truncation limit)’. Size bias occurs because longer traces are more likely to be sampled than shorter ones (Baecher 1983; Jimenez-Rodriguez and Sitar 2006) thus, large fractures are over-represented and this must be considered when estimating the true size distribution. A fourth bias effect is caused by the relative orientation between fractures and the outcrop surface: a fracture is more likely to intersect a surface the more perpendicular their relative orientations are. All these phenomena need to be suitably accounted by the model to interpret the true nature of the rock mass in the best possible way.

The spatial structure of the fractures’ support points is another fundamental aspect in DFN models. The homogeneous Poisson-Boolean point process has been widely used (Baecher et al. 1977; Kulatilake and Wu 1984; Zhang and Einstein 1998; Song and Lee 2001; Jimenez-Rodriguez and Sitar 2006; Hekmatnejad et al. 2019). Other types of point-supporting processes are the doubly stochastic Poisson, or Cox, the Levy–Lee Fractal, the non-stationary Poisson and the Gibbs processes, among others. See e.g., Aldous et al. (1988), Lee et al. (2011) and Hekmatnejad et al. (2019). The decision on the process to be applied depends on the overall breakage pattern of the rock.

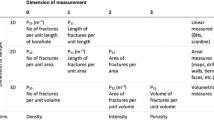
In this work, a novel distribution-free DFN generation technique is developed. It uses a directional-linear KDE to characterize the joint distribution of orientations and trace lengths in a non-parametrical way. The DFN models are calibrated using Monte Carlo realizations of the non-parametric distributions (Zheng et al. 2014 and Zheng et al. 2015). Poisson point process is used for fractures location and these are assumed to be flat and circular in shape. Triangulated surfaces are used to conduct the intersection of a disk with a three-dimensional surface; a MATLAB (MATLAB 2019) function called SurfaceIntersection.m (Tuszynski 2014) based on a triangle/triangle intersection algorithm proposed by (Moller 1998) is used for this purpose. A solution to the Bertrand paradox (Bertrand 1888; Chiu and Larson 2009) is considered to estimate disk sizes from trace lengths. Correction of sampling biases is also addressed. The experimental value of P21, i.e., length of fractures per unit area for each trace map, is fitted through the number of fractures per unit volume (P30), see (Zheng et al. 2017). Field data used to test the model were collected from photogrammetric models of non-planar highwall faces. Disk orientations are obtained by fitting a plane to the 3D coordinates of the polyline fitted to the exposed trace.

In the following sections, data collection and subsequent data processing techniques are described; the mathematical foundations of the model are developed and the calibration process presented. The results obtained from the model are shown, followed by a discussion on the approximation to calculate the trace length distributions and its validity. The influence of the surface on the distribution of trace lengths and the relation between fracture intensities is also investigated.

2 Data Overview

The experimental work was carried out at El Aljibe quarry (Almonacid de Toledo, Spain), where mylonite is mined by drilling and blasting. Discontinuities were mapped from photogrammetric models of the highwall faces of 12 blasts in which the sampling scale was about 10 mm. The blasts were arranged in two test campaigns of six blasts each, located in the same area of the pit. A major extensional fault defines two structural domains DS1 (trace maps TM1-TM6) and DS2 (trace maps TM7-TM12) with different fracture density. Bernardini et al. (2022) give an insight to data collection, discontinuity sets and a classical DFN construction using the FracMan® suite (Golder Associates 2018).

For the analysis, point clouds of the outcrops and discontinuity characteristics (dip, dip direction, and coordinates of polylines’ points) are treated in.csv format. The orientations of the 12 faces are similar with a dip direction of 228.54 ± 4° and a dip of 22.98 ± 3.59° (circular mean ± standard deviation). Because the inspected area is smaller than the area of the complete photogrammetric model, it is cropped with a MATLAB function in a way that the parameter P21 is not affected. The limits of the outcrop surface considered for the calculations are defined by the minimum and maximum coordinates of the traces. The resulting surface areas range between 200 m2 (TM6) and 390 m2 (TM10) approximately.

The number and length of the mapped fractures are shown in Table 1. It also shows the sampling window dimensions, areal fracture density P21 and the percentage of complete, semi-bounded and bounded traces. These are plotted in red, green and blue, respectively in the trace maps of the twelve faces shown in Fig. 1; complete discontinuities correspond to more than 85% of the total, while bounded fractures are observed only in five blasts. Figure 16 shows the stereograms of the experimental poles obtained for each trace map (black dots). There is an increase in the number of fractures marked in DS2 domain (trace maps TM7–TM12), due likely to the effect of the fault mentioned above. This results in a mean P21 of 0.72 m−1 for DS1 and 1.23 m−1 for DS2. The histograms of the lengths of the fractures mapped are shown in Sect. 3.1.2 (Fig. 4).

Table 1 Main characteristics of mapped discontinuities
Full size table
Fig. 1
figure 1

Trace maps of the 12 benches analyzed. Different trace termination types are given with different colors: complete (red), semi-bounded (green) and bounded (blue) censored traces. Camera line of sight (azimuth, elevation) is (128°, 20°) (colour figure online)

Full size image

3 Model Description

The DFN model proposed treats fractures individually instead of considering their belonging to a certain set or family. KDEs are suitable to this end, since they are versatile enough to be used in both directional and linear domains. A Poisson–Boolean point process has been considered to model the location of the support points which is characterized by a constant parameter, P30. Disks are described as flat and circular, although they are modeled as triacontagons.Footnote 1 Fracture sizes and orientations have been considered to be independent. Corrections are implemented to account for orientation, size, truncation and censoring biases and a method has been developed to random sampling the directional-linear KDE; this sampling method is also applicable to non-planar surfaces such as those observed in the field.

3.1 Directional-Linear Kernel to Represent Trace Maps

The DFN is based on a non-parametric distribution using the kernel density estimation for linear-directional data by García-Portugués et al. (2013).

Let Z denote a linear random variable with density fg whose support is all the real numbers. For a random sample of Z, with size n, the traditional linear KDE is given by García-Portugués et al. (2013):

$$\hat{f}_{g} \left( z \right) = \frac{1}{ng}\mathop \sum \limits_{i = 1}^{n} K_{Z} \left( {\frac{{z - Z_{i} }}{g}} \right),\,z \in {\mathbf{\mathbb{R}}}$$
(1)

where KZ is a suitable kernel smoother, and g is the bandwidth of the linear part. In this work we assume a Gaussian smoother. This linear variable may be applied for any length or size of discontinuities equivalently. And let X denote a directional random variable in Cartesian coordinates with density fh that accounts for orientation. The support of such a variable is the q-dimensional hemisphere, denoted by:

$${\omega }_{q}={\omega }_{q}\left({\Omega }_{q}\right)=\frac{{\pi }^{\frac{q+1}{2}}}{\Gamma \left(\frac{q+1}{2}\right)},\,q\ge 1$$
(2)

where ωq is the Lebesgue measure in Ωq, which is the surface area of Ωq and Γ(·) is the gamma function. For spherical data q = 2 and the Lebesgue measure in Ω2 is 2π. Likewise, for a random sample of X, the directional KDE is given by García-Portugués et al. (2013):

$${\widehat{f}}_{h}\left({\varvec{x}}\right)=\frac{{\mathrm{c}}_{h,q}\left({\mathrm{K}}_{\mathrm{L}}\right)}{n}\sum_{i=1}^{n}{\mathrm{K}}_{\mathrm{L}}\left(\frac{1-{{\varvec{x}}}^{{\varvec{T}}}{{\varvec{X}}}_{{\varvec{i}}}}{{h}^{2}}\right),\,{\varvec{x}}\in {\Omega }_{q}$$
(3)

where KL is a suitable kernel smoother, h is the bandwidth of the directional part and ch,q(KL) is a normalizing constant for any \({\varvec{x}}\in {\Omega }_{q}\), which is given by García-Portugués et al. (2013):

$${\mathrm{c}}_{h,q}{\left({\mathrm{K}}_{\mathrm{L}}\right)}^{-1}={\int }_{{\Omega }_{q}}{\mathrm{K}}_{\mathrm{L}}\left(\frac{1-{{\varvec{x}}}^{{\varvec{T}}}{\varvec{y}}}{{h}^{2}}\right){\omega }_{q}\left(d{\varvec{y}}\right)\sim {h}^{q}{{2}^{\frac{q}{2}-1}\omega }_{q-1}{\int }_{0}^{\infty }{\mathrm{K}}_{\mathrm{L}}\left(\eta \right){\eta }^{\frac{q}{2}-1}d\eta$$
(4)

In this case, the von Mises–Fisher kernel smoother has been chosen for simplicity:

$${\mathrm{K}}_{L}\left(\eta \right)={e}^{-\eta }$$
(5)

For a directional-linear random variable (X, Z) with support \({\Omega }_{q}\times {\mathbb{R}}\) and joint density fh,g, the KDE of orientation-sizes may be expressed as (García-Portugués et al. 2013):

$${\widehat{f}}_{h,g}\left({\varvec{x}},z\right)=\frac{{\mathrm{c}}_{h,q}\left({\mathrm{K}}_{\mathrm{L}}\right)}{ng}\sum_{i=1}^{n}{\mathrm{K}}_{\mathrm{L}}{\mathrm{K}}_{\mathrm{Z}}\left(\frac{1-{{\varvec{x}}}^{{\varvec{T}}}{{\varvec{X}}}_{{\varvec{i}}}}{{h}^{2}},\frac{z-{Z}_{i}}{g}\right), \left({\varvec{x}},z\right)\in {\Omega }_{q}\times {\mathbb{R}}$$
(6)

where the notation KLKZ should be understood as:

$${\mathrm{K}}_{\mathrm{L}}{\mathrm{K}}_{\mathrm{Z}}\left(a, b\right)= {\mathrm{K}}_{\mathrm{L}}\left(a\right){\mathrm{K}}_{\mathrm{Z}}\left(b\right)$$
(7)

3.1.1 Log-transformed Kernel for Linear Data

To have a kernel support positive, to prevent negative sizes in the distribution, and to meet the condition \({f}_{g}\left(0\right)=0\), a variable Z* = ln(Z) is introduced (Geenens and Wang 2018). From standard arguments, one has:

$${f}_{Z}\left(z\right)=\frac{{f}_{{Z}^{*}}\left(\mathrm{ln}z\right)}{z},\,z>0$$
(8)

which readily suggests using the estimator \({\widehat{f}}_{{Z}^{*}}\) of \({f}_{{Z}^{*}}\).

$$\widehat{{f}_{Z}}\left(z\right)=\frac{{\widehat{f}}_{{Z}^{*}}\left(\mathrm{ln}z\right)}{z},\,z>0$$
(9)

3.1.2 Optimal Bandwidths

Bandwidth selection of the KDE is an important aspect in non-parametric statistics; the rule-of-thumb (ROT) bandwidth selector hROT for directional data (García-Portugués et al. 2013) is considered in this work:

$${h}_{ROT}={\left(\frac{8{\mathrm{sinh}}^{2}\left(\widehat{\kappa }\right)}{n\widehat{\kappa }\left[\left(1+4{\widehat{\kappa }}^{2}\right)\mathrm{sinh}\left(2\widehat{\kappa }\right)-2\widehat{\kappa }\mathrm{cosh}\left(2\widehat{\kappa }\right)\right]}\right)}^{1/6}$$
(10)

The parameter \(\widehat{\kappa }\) is estimated by maximum-likelihood. The ROT selector is simple but fails when estimating directional densities with multimodality (García-Portugués 2013). This is an issue in geological discontinuity representation, since orientation measurements often present multimodality (in fact the usual procedure is to group traces by families, i.e., different modes). To solve this, we consider only data around the likeliest point in the stereogram, so that the information of the main mode is well fitted. hROT is then calculated from points that do not differ more than 45° from the likeliest point. Figure 2 shows as example the likeliest orientation and the area considered to calculate hROT with Eq. (10) in trace map TM8; the marginal KDE of orientation plotted was obtained with hROT = 0.126. The location of points more than 45° away from the likeliest pole is obtained through a parametrization of the hemisphere–cone intersection (see Sect. 3.3.2).

Fig. 2
figure 2

Example of calculation of hROT. Marginal KDE of orientations (left) and experimental poles (right) for trace map TM8. Dashed lines are the intersection of a cone of 45° with the hemisphere

Full size image

The marginal KDEs of the discontinuity orientation are shown in Fig. 3. They are constructed onto a dense equi-spaced Fibonacci grid through a MATLAB algorithm called SpiralSampleSphere.m (Semechko 2012). The likeliest orientations, which are not evident in all the graphs, are marked with white crosses. Bandwidths from Eq. (10) are given in Table 4.

Fig. 3
figure 3

Marginal KDE of orientations and likeliest points in the stereogram (white crosses) for each highwall face; data is sorted horizontally from top left to bottom right (colour figure online)

Full size image

For the linear part of the KDE, the maximum-likelihood cross-validation MLCV (García-Portugués 2013) is used for bandwidth selection; g is chosen to maximize the following quantity:

$${g}_{mlcv}=\underset{g>0}{\mathrm{argmax}}\mathrm{MLCV}\left(g\right)$$
(11)

where MLCV(g) is given by (García-Portugués 2013):

$$\mathrm{MLCV}\left(g\right)=\left({n}^{-1}\sum_{i=1}^{n}\mathrm{log}\left[\sum_{j\ne i}{\mathrm{K}}_{\mathrm{Z}}\left(\frac{{Z}_{j}-{Z}_{i}}{g}\right)\right]-\mathrm{log}\left[\left(n-1\right)g\right]\right)$$
(12)

Figure 4 shows the histograms (blue bars) and the marginal KDEs (red lines) of pseudo-trace lengths (see next section) calculated with the bandwidths obtained with Eqs. (11) and (12). They are given in Table 3

Fig. 4
figure 4

Marginal KDE of trace lengths for each highwall face. Experimental data (histograms) and KDEs (red lines); data is sorted from top left to bottom right (colour figure online)

Full size image

3.2 Trace Length-to-Fracture Size Distribution Estimation

When a fracture, in this case modeled as a circular disk of a given size, intersects a plane surface of infinite extension, the result is a line whose initial and final points are located on the perimeter of the disk. The exposure of this intersection on the surface is called trace and its length is traditionally called trace length. However, when the surface is non-planar, the intersection between the disk and the surface becomes a polyline. Its length, if measured in 3D, is that we call the ‘true’ trace length. The higher the specific area of the surface, the longer the true length is. This is an inconvenience when calculating fracturing intensity parameters that must be matched with experimental measures since these are closer to the projected length on the mean plane of the surface. This is solved by considering the pseudo-trace length of the chord that a disk forms when intersects the irregular three-dimensional surface.

The probability of a trace obtained from the intersection of a disk with a surface of infinite extension to have a certain length can be approached with the Bertrand’s Paradox (Bertrand 1888). This, however, offers several answers, all plausible, to the interpretation of the concept of randomness Chiu and Larson (2009). Intuitively, one might choose the paradox No. 3, in which the chord center is assumed to be uniformly distributed over a reference radius. This is equivalent to selecting a random point on a reference radius to become the center of a random chord (see Fig. 5).

Fig. 5
figure 5

Scheme for calculation of the pseudo-trace length distribution from a disk size distribution. \(\mathcal{D}\)= 2R disk diameter; Λ radial distance to the center of the chord; \(\mathcal{l}\) incomplete pseudo-trace length; \(\mathcal{L}\) complete pseudo-trace length. The functions and their operations represented on the right of the figure relate to Eqs. (13–20)

Full size image

Following the scheme in Fig. 5, if one starts from the basis of a disk size distribution \(\mathcal{D}\), or a disk radii distribution R = \(\mathcal{D}\)/2 (a triangular distribution has been chosen arbitrarily for the distribution of radii in the right graphs of Fig. 5), and takes any point on a reference radius of any of those disks, a distribution of lengths Λ from the center of the disk to the mentioned point can be formed. For an arbitrary disk radius r, Λ can take values between 0 and r following a uniform distribution, then Λ may be written as the product of two distributions:

$$\Lambda =R\cdot \mathrm{U}\left(\mathrm{0,1}\right)$$
(13)

where U(0,1) is the uniform distribution between 0 and 1. Equation (14) is represented as operation a on the right part of Fig. 5. From Fig. 5, the distributions of \(\mathcal{L}\), R and Λ are related by:

$$\mathcal{L}=2\sqrt{{R}^{2}-{\Lambda }^{2}}$$
(14)

Inserting Eq. (13) in Eq. (14), \(\mathcal{L}\) may be directly obtained from \(\mathcal{D}\):

$$\mathcal{L}=\mathcal{D}\sqrt{1-{\mathrm{U}}^{2}\left(\mathrm{0,1}\right)}$$
(15)

Equation (15) is equivalent to the Warburton’s relationship for estimating trace length probability density, as shown in Appendix A.1, see Eqs. (39–42). Appendix A.2 demonstrates that Eq. (15) is consistent with Bertrand’s paradox No. 3. Equation (15) is represented on the right part of Fig. 5, operation b.

Dividing the pseudo-trace lengths by their respective diameters one may obtain:

$$\frac{\mathcal{L}}{D}=Y$$
(16)

where Y is a random variable whose density function may be expressed as:

$${f}_{Y}\left(y\right)=\frac{y}{\sqrt{1-{y}^{2}}},\,y\in \left[0, 1\right]$$
(17)

A proof of the validity of Eq. (17) is offered in Appendix A.3.

In practice, the outcrop has finite extension so that some traces are censored. Thus, a modification that corrects the censoring bias has to be included. This is accomplished with a mixed random variable Ξ:

$$\mathcal{l}=\mathcal{D}\cdot \Psi$$
(18)

where \(\mathcal{l}\) is the incomplete pseudo-trace length random variable, see Fig. 5 operation d, and Ψ a new random variable resulting from multiplying Y and Ξ, see Fig. 5 operation c, using the properties of product distributions. The following cumulative distribution function has been selected for Ξ:

$$F_{{\Xi }} \left( \xi \right) = \left\{ {\begin{array}{*{20}c} {p\xi^{2}, 0 \le \xi < 1} \\ {1,\user2{ }\xi \ge 1} \\ \end{array} } \right.$$
(19)

where p is a parameter that indicates the proportion of semi-bounded traces over the total number of traces; it is one of the fitting parameters of the model. This function has been built to be a mixed random variable so that it only applies to a proportion of fractures to be treated as semi-bounded; the square has been chosen to enhance the occurrence of long traces. The resulting probability density function of Ψ is:

$${f}_{\Psi }\left(\psi \right)=-p\psi \left(\sqrt{1-{\psi }^{2}}-1\right)\left(\frac{{\psi }^{2}}{\sqrt{1-{\psi }^{2}}{\left(\sqrt{1-{\psi }^{2}}+1\right)}^{2}}+\frac{1}{\sqrt{1-{\psi }^{2}}+1}\right)-2p\psi \mathrm{ln}\left(\frac{\psi }{\sqrt{1-{\psi }^{2}}+1}\right)+\frac{\psi }{\sqrt{1-{\psi }^{2}}},\,\psi \in \left[\mathrm{0,1}\right]$$
(20)

A proof of the validity of Eq. (20) is offered in Appendix A.4.

Equation (18) is of key importance, as it directly relates trace lengths with their respective disk sizes including the censoring bias; moreover, it allows using non-analytic distributions and finite surfaces to obtain the disk size distribution for each orientation, based on the distribution of measurable trace lengths using the definition of ratio distribution:

$${\widehat{f}}_{\mathcal{D}}\left({{\varvec{X}}}_{{\varvec{i}}},D\right)={\int }_{0}^{1}\psi {f}_{\Psi }\left(\psi \right)\frac{{\widehat{f}}_{h,g}\left({{\varvec{X}}}_{{\varvec{i}}},D\psi \right)}{{\int }_{0}^{\infty }{\widehat{f}}_{h,g}\left({{\varvec{X}}}_{{\varvec{i}}},l\right)dl}d\psi$$
(21)

where the KDE \({\widehat{f}}_{h,g}\) is used. A list of quadruplets composed by the Cartesian coordinates of each pole on the unit hemisphere, and the incomplete pseudo-trace lengths, is associated to each trace map. For a given orientation \({{\varvec{X}}}_{{\varvec{i}}}\) (the first three) there is a one-dimensional function of the type \({\widehat{f}}_{h,g}\left({{\varvec{X}}}_{{\varvec{i}}},l\right)\) (see the integrand in Eq. (21)). Such function is normalized to obtain the cumulative distribution function \({\widehat{F}}_{\mathcal{l}}\). This may be done for each Xi so that a disk size distribution is obtained for each orientation. To obtain disks larger than the incomplete pseudo-trace length with which it is associated, the distribution function of experimental incomplete pseudo-trace lengths is used to calculate the probability level of a given pseudo-trace \({l}_{i}\). This level is considered in the distribution function obtained from Eq. (21) to get the respective disk size \({D}_{i}\) through:

$${\widehat{F}}_{\mathcal{D}}\left({{{\varvec{X}}}_{{\varvec{i}}},D}_{i}\right)={\widehat{F}}_{\mathcal{l}}\left({{{\varvec{X}}}_{{\varvec{i}}},l}_{i}\right)$$
(22)

where \({\widehat{F}}_{\mathcal{D}}\) is the distribution function obtained from Eq. (21).

To simplify the calculation, these functions are taken as piecewise linear. Equation (21) is solved numerically for each pseudo-trace. Figure 6 shows the result for trace map TM12 and P = 0.18. As it should, the cumulative distribution of disk sizes (in red) is shifted to the right, so that chord length percentiles are always smaller than the percentiles of fracture size.

Fig. 6
figure 6

Disk size distribution (red) for trace map TM12 from the experimental pseudo-trace length distribution (blue) (colour figure online)

Full size image

3.3 KDE Random Sampling

To construct a DFN model, the directional-linear kernel must be sampled randomly. This is done by (i) random sampling the kernel smoother, (ii) randomly selecting one of the experimental data points with replacement and (iii) adding both values. Random sampling must consider that each point has a different weight, as will be explained in Sect. 3.3.3. The properties of the kernel are associated to all points that make up the support. As a Poisson–Boolean point process, it is characterized by two fundamental properties: (i) Poisson distribution of point counts and (ii) completely random position in the bounded region (Aldous et al. 1988).

3.3.1 Random Sampling of Disk Sizes

Once KDE is sampled, the disk size is taken from the quadruplet associated to each individual discontinuity. A random value depending on the kernel smoother used and the directional bandwidth must be added or subtracted to the disk size. For convenience, it is possible to transform the linear kernel into a quantile function; let be the linear part of the KDE:

$$\mathfrak{L}\left(z,{Z}_{i};h\right)=\frac{1}{zg}{\mathrm{K}}_{\mathrm{Z}}\left(\frac{\mathrm{ln}z-\mathrm{ln}{Z}_{i}}{g}\right)$$
(23)

Since a Gaussian smoother is used, the cumulative distribution function of \(\mathfrak{L}\) is given by:

$$\wp =\frac{1}{2}+\frac{1}{2}\mathrm{erf}\left(\frac{\mathrm{ln}z-\mathrm{ln}{Z}_{i}}{g\sqrt{2}}\right)$$
(24)

where erf is the error function. Solving for z in Eq. (24), one obtains:

$$\mathrm{ln}z=\mathrm{ln}{Z}_{i}+g\sqrt{2}{\mathrm{erf}}^{-1}(2\wp -1)$$
(25)

3.3.2 Random Sampling of Orientations

For the purpose of randomly sampling orientations on the unit hemisphere, points within a certain angular distance around a pole must be selected. This may be accomplished by intersecting a cone with a random opening angle with the hemisphere and then randomly selecting one of the points on the intersection circle. This way, a parametrization of the circle \(\left(\mathrm{sin}\delta \mathrm{cos}t,\mathrm{sin}\delta \mathrm{sin}t\right)\) is carried out by mapping it onto the cone-hemisphere intersection; δ is the cone’s half angle and t a random angle between 0 and 2π. The transformation consists of a rotation and a translation, which reduces to finding a suitable orthonormal basis for \({\mathbb{R}}\) 3. Figure 7 illustrates the orientation sampling process.

Fig. 7
figure 7

Random sampling of orientations

Full size image

For the translation part, the center of the circle is shifted from the origin to:

$${\varvec{c}}=\mathrm{cos}\delta {\varvec{n}}$$
(26)

where c is the intersection of the cone’s axis with the circle’s plane and n is a unit vector which corresponds to the Cartesian coordinates of any disc’s pole. For the rotation part, the z-axis must be mapped to the normal of the intersection circle’s plane. If:

$${\varvec{n}}={\left({n}_{x},{n}_{y},{n}_{z}\right)}^{T}$$
(27)

Then let

$${\varvec{u}}=\frac{{\varvec{n}}\times {\left(\mathrm{0,0},1\right)}^{T}}{\Vert {\varvec{n}}\times {\left(\mathrm{0,0},1\right)}^{T}\Vert }$$
(28)

be a horizontal unit vector and

$${\varvec{v}}={\varvec{n}}\times {\varvec{u}}$$
(29)

With these two vectors, one may construct the parametrization:

$${\varvec{O}}{\varvec{P}}={\varvec{c}}+\mathrm{sin}\delta \mathrm{cos}t{\varvec{u}}+\mathrm{sin}\delta \mathrm{sin}t{\varvec{v}}$$
(30)

δ is derived from the von Mises kernel as a quantile function:

$$\mathrm{cos}\delta ={h}^{2}\mathrm{ln}\left\{\wp \left({e}^{2/{h}^{2}}-1\right)+1\right\}-1,\,\wp \in [\mathrm{0,1}]$$
(31)

If the z coordinate of P is positive, then it is transformed in its antipode, so that it is always on the lower hemisphere.

3.3.3 Weighting Function for Random Sampling

When sampling a joint distribution of disk orientations-sizes within a domain and intersecting them with the highwall face, a disk is more likely to intersect the surface the larger and the closer to perpendicular to the surface it is. Three joint orientation-size distributions are considered: (i) the ‘true’ distribution, (ii) the distribution of disks that intersect the surface, and (iii) the experimental distribution of pseudo-traces. Weighting must be applied to both size and orientation to obtain (i) from (ii), and vice versa. Obtaining a weighted density function from another is accomplished through the following relation (Saghir et al. 2017):

$${f}_{W}(z)=f(z)\frac{w(z)}{\mathrm{E}\left[w(Z)\right]}$$
(32)

where w(x) is an appropriate weighting function and \(\mathrm{E}[\cdot ]\) denotes mathematical expectation. Here f(z) and fW(z) correspond to distributions (i) and (ii), respectively. Equation (32) may be applied for sizes and orientations equally. w(z) may be numerically obtained by computing the ratio between the bin values of the histogram of sizes of disks that intersect the surface (distribution ii) and the histogram of sizes of all the disks generated within the domain (distribution i). These ratios fit well a power law:

$$w(z)=a{z}^{\gamma }$$
(33)

a being a constant and γ an additional fitting parameter of the model. The value of a is not relevant because it vanishes when normalizing. Baecher (1983) already considered a quadratic weighting function.

Figure 8 shows the process of obtaining γ. By way of example, five hundred thousand disks that follow a uniform distribution of diameters between 0 and 3 m and with random orientation are modeled. Green and red histograms in the left graph represent the ‘true’ distribution and the distribution of disks that intersect the surface, respectively. Note the size bias effect caused by the surface. The ratio between bin values of both histograms is shown in the right graph (blue circles). The determination coefficient of fitting Eq. (33) to these points (red line) is 0.996, a = 0.6675 ± 4.7·10–3 and γ = 0.9959 ± 8.3·10–3 at confidence level of 95%. The fact that an infinite planar surface is assumed makes γ \(\approx\) 1. For a non-planar case, γ takes values higher than 1. For the faces studied in this work, γ ranges from 1.13 to 1.48 (see Table 4 in Appendix B); γ is statistically significant in all cases.

Fig. 8
figure 8

Example of calculation of γ. Green and red histograms in the left graph represent the ‘true’ distribution of disks and the distribution of disks that intersect the surface, respectively (colour figure online)

Full size image

The bias correction due to the relative orientation between disks and the intersection surface (the classic Terzaghi correction (Terzaghi 1965) is made by the function:

$${w}_{i}=b\sqrt{1-{\left({{\varvec{\mu}}}^{{\varvec{T}}}{{\varvec{X}}}_{{\varvec{i}}}\right)}^{2}}$$
(34)

where b is a constant and μT is the average normal vector to the surface in case this is non-planar. The value of b is not relevant because it vanishes when normalizing. The vertexNormal.m function in MATLAB has been used to calculate μT which is the normal unit vector to the surface at each of the points of the face. This is a modified version from Mauldon and Xiaohai (2006).

Figure 9 shows the validity of Eq. (34) for a similar simulation, including an infinite planar surface, to that in Fig. 8. The true density function of the dot product \({{\varvec{\mu}}}^{{\varvec{T}}}{{\varvec{X}}}_{{\varvec{i}}}\) is the green histogram in the left graph, and the red one is the distribution of disks that intersect the surface. The ratio between bin values of both histograms is shown in the right graph (blue circles). Fitting Eq. (34) (red line) to these points leads to a determination coefficient of 0.9984 with b = 1.186 ± 7·10–3 at a confidence level 95%.

Fig. 9
figure 9

Weighting function for orientations. Green and red histograms in the left graph represent the ‘true’ distribution of the dot product \({{\varvec{\mu}}}^{{\varvec{T}}}{{\varvec{X}}}_{{\varvec{i}}}\) and the distribution of disks that intersect the surface, respectively (colour figure online)

Full size image

Equations (33) and (34) are combined into a single weighting function for calculating the true distribution from the distribution of disks that intersect the surface:

$${w}_{i}={\left(1-{\left({{\varvec{\mu}}}^{{\varvec{T}}}{{\varvec{X}}}_{{\varvec{i}}}\right)}^{2}\right)}^{-1/2}{{Z}_{i}}^{-\gamma }$$
(35)

3.4 Probabilistic Truncation

Truncation can be described as a ‘perfect filter’ that discards samples when a certain bound is exceeded. This work considers a ‘probabilistic filter’ that groups the sources of error cited in Sect. 1 above and truncates fractures according to a probability level associated with a threshold pseudo-trace length. A simple function that that accepts or rejects traces based on a probability level is the log-logistic distribution function:

$$F\left(l\right)=\frac{1}{1+{(l/\alpha )}^{-\beta }},\,l>0$$
(36)

where α is a scale parameter with units of length that is the trace length with a 50% chance of being observed according to the experimental protocol (e.g., ground sampling distance, operator’s skills, etc.); β is a dimensionless parameter that controls the filter steepness. Low values of β indicate both a large operation range and a low slope, while high β values indicate a sharp transition.

The filter in Eq. (36) is calibrated through probabilistic optimization. The starting point is the histogram of simulated pseudo-trace lengths for a certain trace map. Each trace has its respective length and, therefore, a probability level of being or not being observed by the operator according to Eq. (36). α and β are estimated such that experimental and simulated pseudo-trace length histograms match. A randomized algorithm based on the binornd.m routine has been developed in MATLAB. It consists in sampling a Bernoulli distribution with a vector composed of n probabilities, n being the number of disks that intersect the surface. The result is a logical vector with 0 when the trace is not observed and 1 when the trace is observed. This process is repeated one thousand times for the whole set of pseudo-trace lengths in each highwall face; for each of those realizations, a Kolmogorov–Smirnov test between the experimental and simulated histograms is performed. The average of the test P values is the parameter to be maximized. The number of disks deemed observed after this filtering is N. Figure 10 shows as an example the effect of the probabilistic filter in the simulated pseudo-trace lengths of TM3. Note that there are many small traces that have not been observed as their sizes were probably below the resolution of the experimental discontinuity detection system.

Fig. 10
figure 10

Probabilistic filter with α = 1.039 m and β = 2.375 for pseudo-trace lengths of TM3. Histogram of simulated pseudo-traces (blue), histogram of likely observed pseudo-traces (red) and marginal KDE (cyan line) of the observed traces

Full size image

4 Model Calibration and Results

The objective of the model is to estimate the value of fracture intensity P30 that replicates the experimental P21 value for each trace map. The process followed to calibrate the DFN model is summarized in Appendix C; (i) Bandwidths h and g are calculated according to Eqs. (10), (11) and (12). (ii) The pseudo-trace length KDE for each orientation is calculated using Eq. (6). (iii) The distribution of disk sizes is estimated through Eqs. (18), (21) and (22); an initial value 0.3 is chosen for the ratio p between semi-bounded traces and the total number of traces. (iv) A large number of disks are sampled according to Eqs. (26) and (30) within a domain large enough to engulf each outcrop; a cubic volume of 40 m side and two million disks (equivalent to a P30 of 31.25 m−3) are considered initially. The exponent γ of the weighting function in Eq. (35) is initially set to 1 for all the faces. In a second iteration, p and γ are recalculated from the results of the previous iteration: p is obtained by counting the number of semi-bounded traces over the total number of traces and γ by following the procedure described in Sect. 3.3.3. These values are checked for convergence:

$$\left|{p}_{i}-{p}_{i-1}\right| \wedge \left|{\gamma }_{i}-{\gamma }_{i-1}\right|<\epsilon$$
(37)

Steps (iii) to (iv) are repeated until convergence. Then (v) the probabilistic truncation process in Sect. 3.4 is applied to fit the truncation function parameters α and β in Eq. (36). The resulting mean number of traces that intersect the face after applying the probabilistic filter, N, is obtained in this process.

An estimator of P30, i.e., number of disks to be simulated within the domain to obtain the P21 observed on the surface in the field is:

$${\widehat{P}}_{30}=\lceil\frac{{\sum }_{i}{l}_{i}}{\overline{l} }/\frac{N}{TF}\rceil/V$$
(38)

where li is the pseudo-trace length of a trace observed experimentally, \(\overline{l }\) is the mean of the pseudo-trace length KDE, TF is the total number of fractures generated within the domain and V the volume of the domain.

The parameters of the model (h, g, p, γ, α and β) are summarized in Table 4 for the twelve highwall faces. Fracture intensities P30, P21 and P32 are given and also the percentage of fractures that intersect the outcrop over the total number of disks generated, N/TF. An example of DFN model is shown in Fig. 11, see others in Fig. 20, Appendix B. The scale parameter α of the log-logistic function, Eq. (36), decreases from TM1 to TM12 (Table 4). This implies that shorter traces are marked for the last faces. This might be likely caused either by local changes in rock mass due to the existence of the extensional fault that crosses the highwall faces TM11 and TM12, see Bernardini et al. (2022) for additional information. Figure 12 shows the fracturing intensity parameters for the twelve trace maps. They are in general higher for faces in DS2 domain (TM7–TM12), and they all follow a similar trend except in TM11 and TM12, where P30 increases and P21 and P32 do not. This may be explained as Table 1 shows due to an increase in the number of fractures, and a decrease in their mean sizes (raised to the second power), especially in TM12.

Fig. 11
figure 11

DFN model for trace map TM2. Disks in inverse pole figure color code (fractures with similar orientation in similar tone)

Full size image
Fig. 12
figure 12

Fracture intensity parameters P30, P21 and P32 for the faces studied

Full size image

To illustrate the model performance, Fig. 13 shows, for TM1: traces (chords) obtained from a simulation (green lines in the left graph); the marginal KDE of pseudo-trace lengths obtained from experimental data (red curve in the central graph), together with the histogram of pseudo-trace lengths obtained from the simulation (blue bars); and the map of experimental and simulated poles (black and red dots, respectively, right graph). The model is stochastically similar to the observations. The number of fractures observed to intersect the surface is 66 that coincides with the average number of simulated disks that intersect the surface. All other cases are shown in Fig. 16.

Fig. 13
figure 13

Model results for face TM1. Left: pseudo-traces, shown as green segments (the surface has some transparency and darker lines are pseudo-traces located behind the surface). Center: marginal KDE of pseudo-trace lengths obtained from experimental data (red curve: experimental; blue bars: histogram of pseudo-trace lengths from the simulation). Right: map of experimental (black dots) and simulated (red dots) poles (colour figure online)

Full size image

5 Discussion

To assess the validity of the proposed DFN model, the relations proposed by Zhang et al. (2002) for trace lengths and disk sizes must be verified and typical relations among fracture intensities must be met.

The common relations between true disk sizes and pseudo-trace lengths distributions Zhang et al. (2002) have been used to assess Eq. (17) in Sect. 3.2. Such relations were derived for some common distributions of trace length, such as lognormal, negative exponential and gamma, assuming the same distribution for both disk size and pseudo-trace length. Three numerical simulations have been performed with disk sizes following: (i) a lognormal distribution with μ = 0.5 m and σ = 0.25 m, (ii) a negative exponential distribution with μ = 0.25 m, and (iii) a gamma distribution with α = 2 and β = 0.5. The resultant distributions obtained with Eqs. (17) and (35) are shown in Fig. 14. Green histograms correspond to the true disk size distribution and the blue ones the pseudo-trace lengths. The distributions of disks that intersect the surface have also been plotted (red), as these distributions are used for calculating the pseudo-trace lengths. Table 2 summarizes the means and variances (m and v) of the different distributions obtained in the simulations. They are asymptotically equal to those obtained from the relationships provided by Zhang et al. (2002) (for a two million disk simulation they are equal to the third significant digit). Note in Fig. 14 that the distribution type of disk sizes and traces is not necessarily preserved; this is quite obvious for the lognormal and the negative exponential cases. Even if the means and variances are well estimated, the actual distributions can be grossly different.

Fig. 14
figure 14

Lognormal (left), negative exponential (center) and gamma (right) distributions of true disk sizes (green), size of disks that intersect the surface (red) and pseudo-trace lengths (blue) (colour figure online)

Full size image
Table 2 Relation between parameters (mean, m and variance, v) of the true disk size (subscript D) and the pseudo-trace length (subscript L) distributions; same colors as in Fig. 14 have been used
Full size table

A linear relationship would be expected between the fracture intensities P21 and P32 for domains with similar properties (Dershowitz and Herda 1992; Mauldon 1994; Wang 2005), with a ratio P21/P32 between 0 and 1. This applies irrespective of the disk size distribution. To verify this, values of P32 and P21 from Table 4 have been plotted, grouping them by the domain they belong to, in Fig. 15. Values of P21/P32 are also given in Table 4. Correlation coefficients are shown in the upper left part of the graph. Both P values are lower than 0.05 which indicates the relations are significant. The same relations were tried between P30 and P21, and P30 and P32, in this case without significance to the 0.05 level. P30 provides an incomplete fracture description as it only indicates the density of support points while the size of the fractures (unlike P21 and P32) is missing in it. In fact, there is probably no reason for P30 to be correlated, in general, with P32 or P21 though, for a given size distribution of fractures, more fractures will likely encompass more traces (and longer total trace length) on an intersecting surface, and more fracture surface per unit volume. To assess differences between the model developed in this work and traditional DFN models, fracture densities of the domains DS1 and DS2 built with FracMan® suite Bernardini et al. (2022) are plotted for comparison, as cyan and orange points, in Fig. 15. They fall acceptably well in the linear trends of each pair of fracture densities, especially for the DS2 case (red and orange points).

Fig. 15
figure 15

Linear correlations between P32 and P21 for the 12 highwall faces studied. DS1 (blue and cyan) and DS2 (red and orange) (colour figure online)

Full size image

The use of traditional DFN codes implies inevitably: (i) initial manual sectorization of fractures, which may introduce some bias because of the operator’s criterion; to this, the time spent in interpreting the data must be added; (ii) parametrical characterization of the families, which involves selecting some probability distribution functions based on Kolmogorov–Smirnov tests; and (iii) calibration of an intensity parameter for each family of fractures, which entails increasing computational time with increasing number of families. In our own experience with traditional codes, the third step consumes the most computational time. The calibration process of the model proposed here saves considerable amounts of time in this step, since the KDEs considers all fractures independently of the family they might belong to. As an example, the computational time the code consumes in completing an iteration for TM10 is about 75 min on a 2.2 GHz MSI GF62 8RD laptop. Most of the time, 65.2%, is spent in solving the triangle–triangle intersections that is dependent of the quantity of disks, the number of sides of each disk and the number of triangles that make up the intersection surface, a 21% in self-time (third step in Sect. 4), a 5.5% in calibrating the probabilistic filter, a 5.3% in random sampling and the rest in other subroutines.

6 Conclusions

A novel distribution-free DFN generation technique is developed, making use of directional-linear KDE to non-parametrically characterize jointly the distribution of fracture orientations and trace lengths. The non-parametric approach does not require a classification of fractures into sets as parametric models do and does not demand any statement on a particular functional distribution of trace lengths or disk diameters derived thereof.

The mathematical modeling and the application steps are explained thoroughly, with the inclusion of numerical tests of consistency where required. Bias corrections are provided for censoring, size, orientation and truncation. Censoring is addressed using a new calculation method that includes semi-bounded traces. Size and orientation biases are jointly addressed using a new weighting function. The truncation bias is corrected by a probabilistic filter capable of incorporating fractures to the DFN shorter than those observed in field measurements. This endows the model with a certain scale-independent character, not the case of traditional parametric DFN models.

The model has been applied to twelve trace maps obtained from photogrammetry of highwall faces. Disk orientations were obtained by fitting a plane to the 3D-polyline defined by the traces. The DFN models are calibrated using Monte Carlo realizations of the non-parametric distributions. A Poisson point process is used for fractures location, assumed to be flat and circular in shape. Solution No. 3 of the Bertrand paradox has proved to be effective to estimate disk sizes from trace lengths.

The experimental value of P21, is fitted through the number of fractures per unit volume (P30). The resulting fracture intensities P21 and P32 are linearly related, which supports the model validity. These intensities have been discussed with classical DFN generation systems.

While the non-parametric model does not require an assumption of a distribution type for traces and fracture diameters, its results meet the classical relations between mean and variance of trace lengths and disk diameters. It is shown however, that the distribution types of trace lengths and diameters can be markedly different, a feature that does not affect kernel-based non-parametric DFNs.