Evaluation of the Diametrical Core Deformation and Discing Analyses for In-Situ Stress Estimation and Application to the 4.9 km Deep Rock Core from the Basel Geothermal Borehole, Switzerland

Abstract

The in situ state of rock mass stresses is a key design parameter, e.g., for deep engineered geothermal systems. However, knowledge of the stress state at great depths is sparse mostly because of the lack of possible in situ tests in deep boreholes. Among different options, core-based in situ stress estimation may provide valuable stress information though core-based techniques have not yet become a standard. In this study we focus on the Diametrical Core Deformation Analysis (DCDA) technique using monzogranitic to monzonitic rock drill cores from 4.9 km depth of the Basel-1 borehole in Switzerland. With DCDA the maximum and minimum horizontal stress (S_Hmax and S_hmin) directions, and the horizontal differential stress magnitudes (∆S) can be estimated from rock cores extracted from vertical boreholes. Our study has three goals: first, to assess photogrammetric core scanning to conduct DCDA; second, to compare DCDA results with borehole breakout and stress-induced core discing fracture (CDF) data sets; and third, to investigate the impact of rock elastic anisotropy on ∆S. Our study reveals that photogrammetric scanning can be used to extract reliable core diametrical data and CDF traces. Locally aligned core pieces showed similar S_Hmax orientations, conform to borehole breakout results. However, the variability of core diametrical differences was large for the Basel-1 core pieces, which leads to a large spread of ∆S. Finally, we demonstrate that core elastic anisotropy must be considered, requiring robust estimates of rock elastic moduli, to receive valuable stress information from DCDA analyses.

1 Introduction

Knowledge of rock mass stresses is essential for engineering designs of, e.g., tunnels, underground mines, or deep geothermal reservoirs. Rock stress data can come from different sources such as earthquake focal plane solutions, borehole-based and core-based stress measurement techniques (e.g., Zang and Stephansson 2010; Heidbach et al. 2016). Depending on the applied method, stress data are derived from various spatial scales (regional to core specimen size), can contain different details of information (faulting regime, stress component orientations, to full stress tensor), and may have different levels of quality and confidence (e.g., Heidbach et al. 2010: Table 2). Where possible, multiple sources of stress information should be considered to obtain a comprehensive understanding of stresses at depth and increase estimate reliability. Boreholes are drilled and cored to explore lithology, fractures, rock and rock mass mechanical properties, and to conduct borehole testing and logging. However, the obtained drill cores are rarely considered as a prime source of stress information even though core-based stress analyses were tested and discussed since about the 1960s (e.g., Obert and Stephenson 1965; Röckel 1996) and have much advanced since then together with a better understanding of the stresses that surround boreholes. Core-based stress measurements can be grouped into methods that investigate (1) drilling-induced, macroscopic core fractures (e.g., discing fractures, petal fractures; e.g., Kulander et al. 1990; Li and Schmitt 1998; Hakala 1999; Schmitt et al. 2012, and references cited therein), (2) microscopic core damage (i.e., anelastic strain, Kaiser effect; e.g., Teufel 1983; see overview given by Zang and Stephansson 2010), and (3) core elastic deformation (e.g., Funato et al. 2012; Funato and Ito 2017).

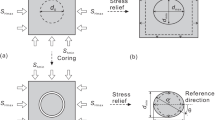
In this work, we investigate drilling-induced Core Discing Fractures (CDFs) and conduct Diametrical Core Deformation Analysis (DCDA) of rock cores extracted between 4909 and 4918 m drilled depth in the sub-vertical Basel-1 geothermal well in Switzerland to characterise stress at great depth. CDFs are oriented about perpendicular to the core axis and form due to stress redistribution at the borehole bottom upon coring as tensile fractures in rocks under high in situ stresses (e.g., Stacey 1982; Dyke 1989; Li and Schmitt 1997). Plumose markings and many modelling results support the tensile nature of CDFs (Song and Haimsson 1999, and references therein; Bankwitz and Bankwitz 1997). According to the elasto–plastic model results by Corthésy and Leite (2008), CDFs initiate in the centre of the core. This stands in contrast to their and other elastic model results suggesting that failure initiates at the core circumference, and to numerical investigation by Wu et al. (2018) who argued that the fracture origin depends also on the stress regime, i.e., only in thrust-faulting regimes CDFs originated in the middle of the core stub. In addition, Corthésy and Leite (2008) showed that progressive rock damage and failure have to be included in numerical analyses which aim at estimating in situ stresses from mapped CDFs. In vertical boreholes, CDFs are indicators for high horizontal stresses and the disc asymmetry can be used as an indicator if the vertical stress is a principal stress (e.g., Dyke 1989). According to Lim and Martin (2010), core discing initiates when the maximum principal stress normalised by the rock tensile strength is 6.5. The thickness of the discs can be used to estimate the stress magnitude, although the generality of the proposed relationship is not established; a small disc height to diameter ratio indicates greater stress (Kaga et al. 2003; Matsuki et al. 2004; Lim et al. 2006; Lim and Martin 2010). Furthermore, the shape of the disc (flat or saddle-shaped) can be used to estimate the ratio of horizontal stresses in vertical boreholes and, in case of saddle-shaped discs, the axis given by the saddle low points marks the direction of maximum horizontal stress (e.g., Dyke 1988; Maury et al. 1988; Bankwitz and Bankwitz 1997; Lim et al. 2006; Fig. 1a). For further discussion on CDFs see, e.g., Wu et al. (2018).

Fig. 1

a Sketch of a single core disc with a saddle shape. The saddle trough axis can be used to estimate the direction of S_max (and S_Hmax in the case of a vertical borehole). b Concept of using rock core radial expansion upon drilling. A core with assumed circular initial cross-section with a diameter d₀ will expand in the direction of S_max more (d_max) than in the direction of S_min (d_min) (sketch modified after Funato and Ito (2017))

Extraction of rock from a compressed rock mass leads to stress relaxation and expansion of the rock. This expansion occurs in all directions and may include elastic and anelastic behaviour. In the case of DCDA, it is assumed that rotary drilling produces initially a perfectly cylindrical core geometry which is then relaxing from the in situ stress with all radial core deformation being elastic (Funato et al. 2012). Measuring the core radii is used to infer in situ stress directions (e.g., the direction of the minimum and maximum horizontal stress, S_Hmax and S_hmin, in case of a vertical borehole), and the differential radial stress magnitude, ∆S, if the elastic properties of the rock are known (Fig. 1b).

In this study, we present a novel technique to record core fractures and measure core diameters using photogrammetric scanning, in contrast to, e.g., Funato et al. (2012), who used an optical micrometre for DCDA. In addition, we compare results of CDFs and DCDA from the Basel-1 core with borehole breakout data obtained previously (Valley and Evans 2009). Finally, we explore the impact of rock transverse isotropy on stress estimation from DCDA with three-dimensional numerical modelling.

2 Background

2.1 The Borehole Basel-1

The borehole Basel-1 (BS-1) was drilled with a T45 mud rotary drill rig by KCA Deutag between May and October 2006 in the city of Basel at 611,810.054, 270,535.874 (Swiss CH1903 coordinates) to a depth of 5009.4 m below the rotary table (RT; Fig. 2a). The elevation of the RT was at 259.34 m a.s.l. and 9.14 m above ground. All depths in Basel-1 given in this article are measured along hole from the rotary table unless stated otherwise. In the sedimentary rock cover (see Sect. 2.2) the telescoping diameters of the BS-1 borehole range from 33″ in the first 33.1 m to 14 3/4″ at 2603.5 m. In the crystalline basement the hole diameter is 9 7/8″ down to 4850 m, 8 3/8″ where a rock core was taken by Baker Huges using a surface-set diamond core bit on October 12th, 2006 (between 4909.0 and 4917.7 m; Sect. 3.1), and 8 1/2″ below 4917.7 m. The BS-1 hole is cased to a depth of 4638 m, and the remaining 371.4 m were kept uncased. Except where the rock core was obtained, the borehole was drilled destructively, and drill cuttings were collected every 5 m. The borehole direction was surveyed with an electromagnetic survey sonde to a depth of 4975.5 m. Until 3500 m depth the borehole is about vertical with a maximum deviation from vertical of 3.7° toward west at 2120 m depth. Below 3500 m the deviation from vertical increases to 7.9° toward north-west until a depth of about 4600 m, and ranges between 6.0° and 7.8° thereafter (Fig. 2b,c). The bottom of the borehole locates at 302° and 206 m horizontal distance from the standpipe (Häring et al. 2008, Geothermal Explorers 2007).

Fig. 2

a Simplified tectonic map modified after Valley and Evans (2009), together with the location of the Basel-1 (BS-1) well in the south-eastern corner of the Upper Rhine Graben. b Lithological profile, trajectory, and deviation of the Basel-1 well. c Top view of the Basel-1 well trajectory

2.2 Lithology along the Basel-1 well

The lithological profile along the Basel-1 borehole was determined primarily from analysis of drill cuttings. In addition, an about 9 m long drill core sample taken at 4.9 km depth (see Sect. 3.1) was available for lithological analysis. The crystalline basement is overlain by Quaternary, Cenozoic, Mesozoic (Jurassic and Triassic), and Permian sedimentary rocks with a collective vertical thickness of 2504 m (Fig. 2b). The borehole section between 2420 and 2516 m consists of a ‘transition zone’ containing Rotliegend siltstones and crystalline rocks. The crystalline basement is mainly composed of granitic rocks, and to a minor extent, of lamprophyric and aplitic dykes. The compositions of the granitic rocks range from hornblende-bearing, quartz-rich biotite-granites (coarser-grained) at the top of the basement to monzogranites and monzonites with decreased contents of quartz (finer-grained) at deeper borehole sections. Geochemical analysis suggests that the granitic rocks are of I-type (i.e., igneous magma origin), in contrast to the S-type granites (i.e., magma originating from partial melting of sedimentary source rocks) typically found in the southern Black Forest (Kaeser et al. 2007).

The core sample contains no natural fractures (joints or faults), as elsewhere identified along the Basel-1 well (Ziegler et al. 2015; Ziegler and Evans 2020), and consists of monzogranite and monzonite with an isotropic to slightly anisotropic structure (i.e., oriented, up to 5 cm long potassium feldspar phenocrysts and elongated clusters composed of hornblende and biotite; see Fig. 3 and Sect. 3.1). The monzogranites are brighter due to less biotite and hornblende and coarser-grained than the monzonites, which are finer-grained and have partly a porphyritic texture (compare, e.g., piece 4-1 with piece 4-2 in Fig. 3). In addition, rounded, fine-grained mafic xenoliths occur in the core (pieces 3-1 to 3-4 in Fig. 3).

Fig. 3

Overview photographs of the Basel-1 core trays and pieces as of 2016. We numbered pieces with “X–Y”, where X is the tray number and Y is the piece number, increasing with greater depth. The given depth ranges are the reported cored lengths given on the ten core trays. No core losses during drilling were noted. The grey sections are gaps originating from previous sampling and testing. Note that the initial core markings (red and black lines) have errors, i.e., the core pieces were not always aligned well. Green frames indicate locally aligned core pieces with perfectly matching ends

2.3 Rock Mechanical Properties

The mechanical properties of the Basel monzogranite summarised in Table 1 were determined by a single multi-stage confined compression test performed on a 34 mm core plug (Braun 2007) and by fullwave sonic and density log analyses. These data have been presented and analysed in Valley and Evans (2019). The interpretation of these data is ambiguous for both strength and elastic modulus. For the elastic modulus, there is an unexplained discrepancy between lab measurements and in situ estimation from sonic and density logs, that cannot be explained by the expected differences between static and dynamic moduli. For strength, the friction seems to be strongly confinement dependent. Since we are considering processes occurring in the core and around the wellbore, we use here the parameters derived for low confinement conditions. Braun (2007) estimated a tensile strength of 10.6 MPa by extrapolating a low-confinement Coulomb failure criterion. Using an approach from Perras and Diederichs (2014) based on the non-linear Hoek–Brown failure parameters, Valley and Evans (2019) estimated a tensile strength of 4 MPa. The latter seems low for crystalline rocks, while the back projection of the Coulomb failure criterion tends to overestimate tensile strength. Thus, we consider that a range from 4 to 11 MPa provides reasonable bounds on tensile strength. We refer to Valley and Evans (2019) for further details on these interpretations.

Table 1 Estimates of mechanical properties of Basel monzogranite (Braun 2007; Valley and Evans 2019)

2.4 Stress State

Various data sets from the Basel geothermal project were used to estimate the stress state. This includes injection pressure analyses reported in Häring et al. (2008), core measurements based on p- and s-wave velocity anisotropy upon loading (Rock Anisotropy Characterisation on Sample, RACOS^®; Braun 2007), borehole failure analyses (Valley and Evans 2009, 2019), and earthquake focal mechanisms analyses (e.g., Terakawa et al. 2012). We give a summary of these estimates here with the objective to present the expected stress state at the depth of the Basel core (Table 2).

Table 2 Estimate of the stress state at the depth of the Basel core (Valley and Evans 2009, 2019)

The orientation of S_Hmax of N144° on average along the entire granitic section is the most certain stress component estimated along the Basel-1 well, determined by the average orientation of almost continuous borehole breakouts (Valley and Evans 2009) and validated by inversion of focal mechanisms (Terakawa et al. 2012). At the depth of the core, the average S_Hmax orientation estimated from breakouts observations is N142°.

The vertical stress component is estimated by the integration of density logs and best approximated by a stress gradient of 24.9 MPa/km (Valley and Evans 2019). At the depth of the Basel core of 4894.3 m (True Vertical Depth (TVD) below ground surface), this implies a vertical stress magnitude of 122 MPa.

The maximum downhole pressure of 74.4 MPa reached at the casing shoe at 4638 m depth during massive fluid injection is considered as the most reliable indicator of the S_hmin magnitude. During a formation integrity test (FIT) performed at 2602 m a maximum downhole pressure of 34 MPa was reached but was still rising. Thus, this pressure likely underestimates the S_hmin magnitude. With only one reliable estimate of the S_hmin magnitude at 4638 m, the minimum principal stress gradient remains uncertain. Considerations stemming from the observation that breakout width diminishes with increasing depth suggest that the stress gradient is low (Valley and Evans 2019). Taking the possible limit scenario from these considerations, S_hmin magnitude at the depth of the Basel core (4894 m TVD below ground level) is bound between 76 and 79 MPa. This is somewhat less than the estimate of 84 MPa based on RACOS® measurement by Braun (2007).

The magnitude of S_Hmax is most uncertain. Braun (2007) suggested a stress magnitude of 160 MPa at 4910 m depth based on RACOS® measurement. However, Häring et al. (2008), who reported this result, suggested to treat it with caution. In their inversion of focal mechanisms, Terakawa et al. (2012) computed a mean stress ratio, $\overline{R} = \frac{{\sigma_{1} - \sigma_{2} }}{{\sigma_{1} - \sigma_{3} }}$, of 0.36 with a strike-slip regime, but with broad uncertainty with a one standard deviation (1σ) confidence range from 0.3 to 0.6. Assuming a strike-slip stress regime and the estimates for S_hmin and S_v above results in an S_Hmax magnitude of 147 MPa with 1σ range from 141 to 188 MPa, considering the reported mean ratio. A more recent focal mechanisms study of the Basel induced seismicity data (Kraft and Deichmann 2014) showed a mix of strike-slip and normal mechanisms, which suggest that a normal stress regime should not be excluded. Taking Terakawa et al. (2012) stress ratio in a normal stress regime implies an S_Hmax magnitude (mean stress ratio) of 106 MPa with a 1σ range from 95 to 109 MPa. An alternative estimate based on borehole breakout width observations and analyses (Valley and Evans 2019) suggested that the S_Hmax depth gradient is small. The absolute magnitude of S_Hmax is however difficult to estimate due to uncertainty in rock strength parameterisation. Their best estimate of the S_Hmax magnitude at the depth of the Basel core (4894 m TVD below ground level) is 115 MPa, suggesting a stress regime at this depth which is at the limit between normal and strike-slip conditions, i.e., consistent with focal mechanisms observations of Kraft and Deichmann (2014).

3 Methodology

3.1 Core Specimen

The BS-1 borehole was cored continuously from 4908.10 to 4917.19 m depth. The core diameter is 101 mm. 9.09 m of core were obtained (i.e., cumulative length as written on core trays with 100% core recovery; cf., Geothermal Explorers (2007) who reported a depth range from 4909.0 to 4917.7, i.e., 8.7 m cored length; Sect. 2.1) and cut into about 1 m long sections. At the time of our work 68 core pieces, some of which have saw-cut ends, were available for analyses (Fig. 3). Many of the core pieces are drilling-induced core discs with thicknesses mostly between two and four centimetres. Missing core pieces were used previously for petrographic analyses and a rock-mechanical test (Braun 2007). Each piece in this analysis was numbered with core box number-core piece number with increasing numbers from top to bottom, e.g., 4–2 (box no. 4, piece no. 2). Monzonite makes up the major portion of the BS-1 core (about 5.76 m), the monzogranite comprises about 3.03 m and the mafic enclaves about 0.3 m (for further details see Sect. 2.2). The transitions of coarser-grained monzonite to smaller-grained monzogranite and back to monzonite at about 4911.2 and 4914.5 m are reflected in the total gamma radiation values of 230–260 API between ca. 4910.7 m and 4914.9 m compared to 180–200 API in the surrounding. However, the gamma ray logging depth and core (driller’s) depth seem to have an offset of about 0.4–0.5 m.

To document the core, we used a DMT CoreScan3 to record core overview images at 10 pixel/mm resolution and unrolled scans with a resolution of 40 pixel/mm. Prior to the scans, we fitted all core pieces and established a reference line (see used convention in Fig. 4a). However, not all core pieces could be oriented with each other so that in this work we compare data sets piecewise. Note that the rock core was drilled without an orientation tool and no natural fractures were intersected, which could have facilitated the reorientation of the core by comparison with acoustic borehole wall images. In addition, the initial core orientation marks (a red and a black line) do not provide a stable orientation reference along the entire core length.

Fig. 4

a Sketch of the longitudinal core reference line and angle convention used in this study. Photographs of b the coordinate measuring of piece 7–1 using a STRATO-Apex 9106© CNC CMM at Mitutoyo, Urdorf (CH) and c representative CMM data (black dots) of one measured slice from core piece 7-1 together with fitted ellipse (dotted grey line), d_min (orange line), d_max (blue line), ∆d, and orientation of d_max. Note that we subtracted 50 mm from the measured radial values to render the ellipticity perceptible

3.2 DCDA

3.2.1 Core Geometry from Coordinate Measuring Machine

The surface geometry of four core pieces (4-1, 5-2, 6-4, and 7-1; Table 3) was measured with a Mitutoyo Strato Apex 9106 Coordinate Measuring Machine (CMM) in a climate-controlled room. In order that the core pieces obtain a constant temperature, they were stored in the testing room about 48 h prior to the measurements. Figure 4b shows the CMM setup with core piece 7-1. The used CMM sensor applied a contact force of about 0.2 N to measure the radial differences with respect to a reference cylinder of 50.5 mm radius. To define the reference cylinder axis, the CMM measured the positions of the core surface along two planes at the bottom and top ends of the core specimen, and the plane centroid points then defined the core axis. For each core piece, the radial measurements were performed in 1 mm steps along lines parallel to the cylinder axis spaced every 10° around the circumference of the sample (proceeding counter-clockwise from the reference line; Fig. 4a). The resolution of the measured coordinates is approximately 0.02 μm. The length (L) measuring error E_150,MPE (according to ISO 10360-2: 2009) is specified with 0.9 μm + 2.5L/1000 μm with the used SP25M scanning probe and offset probe tip (Fig. 4b). In this study L can be defined by our core diameter of about 101 mm and the length measuring error is 1.15 μm.

Table 3 Overview of the Basel-1 rock core pieces and conducted analyses

We used a direct least fitting approach from Halíř and Flusser (1998) to fit ellipses to each 1 mm spaced slice of 36 points obtained from CMM measurements describing core cross-sections and to calculate the maximum and minimum ellipse diameters, which we use as estimates of the maximum (d_max) and minimum (d_min) core diameters. Fitting an ellipse using 36 data points while in theory five points would be sufficient to constrain an ellipse has the implicit effect of reducing the impact of potential outliers that could arise from drilling induced core rugosity. A representative example of a fitted ellipse to our data is shown in Fig. 4c. In addition, we obtained the direction of d_max. We then compared the ratio of d_max to d_min and the direction of d_max with the results of the photogrammetric (Section 3.2.2), core discing (Section 3.3), and radial ultrasonic velocity analyses (Sect. 3.4).

3.2.2 Core Geometry from Photogrammetric Scanning

We conducted photogrammetric 3D scans of 32 core pieces from boxes 1–7, 9, and 10 using a GOM ATOS 300 Core© scanner under constant (± 1 °C) temperature conditions (Table 3). The accuracy of the core scanner ranges between about 10 and 20 μm. To aid the generation of the photogrammetric models, we coated the core pieces sparsely with a removable, about uniform, < 10 μm thin layer of antireflection coating (Helling 3D anti-glare spray with average particle size of 2.8 μm). Per core piece we made many 10 s of scans from different viewing angles, by mounting the core piece on a rotatable plate (Fig. 5a). Each scan results in a point cloud and triangular mesh. For referencing, markers were placed on the core. The GOM Scan© software references the individual point clouds and in a polygonisation step creates a single point cloud and triangular mesh that represents the 3D surface of the core (Fig. 5b). The data is saved as an stl-file. During polygonisation the sensor-specific measurement noise is considered, mesh errors are eliminated, data gaps at the reference point locations are filled, and the point clouds are smoothed and thinned. The final point clouds have a density of about 4000–5000 points per 1 mm slice in the z direction (see below). To remedy the lack of orientation inherent to the models, 2–3 cm long toothpicks were placed on the reference line on each core prior to scanning to indicate the position of the reference line and the “up” direction (i.e., positive z, towards the borehole collar), and are visible on the surveyed pieces.

Fig. 5

a Exemplary photogrammetric core scanning using a GOM ATOS 300 Core scanner. b Shaded mesh of the photogrammetrically scanned surface of core piece 7–1 (cf., Fig. 4b, c). A disc fracture surface at the upper end of the core piece and faint traces of non-detached core discs are visible. The 3D model of the 22 cm long core piece consists of 1.22 million points (~ 14 points/mm²)

After the scanning process, the photogrammetric models were oriented, i.e., the cylindrical model axis was defined and oriented vertically with the cylinder axis coordinates set to x = 0 and y = 0 and with the toothpick pointing “up” and the model was rotated so that the reference line is at y = 0. We evaluated two methodologies to orient the cylindrical point clouds. The first method is a manual, visual alignment of the core’s surface line to the z-axis using a high magnification of the 3D model in CloudCompare. The second method uses the RANSAC shape detection algorithm by Schnabel et al. (2007) as plugin in CloudCompare to fit a cylinder with circular cross-section to the point cloud, and the fitted end-faces of the cylinder, together with the point cloud, are horizontally levelled. To test the two approaches, we used two point clouds that describe perfect cylinders with a radius of 50 mm, lengths of 30 mm and 300 mm, point spacing in the longitudinal direction of 0.02 mm, a random orientation, and analysed the resulting error (i.e., the ellipticity of 1 mm thick horizontal slices of oriented cylindrical point clouds). The lengths of the two generated point cloud cylinders represent the range of core piece lengths, and the point cloud density was set to 4000–5000 per 1-mm slice, similar to actual photogrammetric models. To simulate the randomness of the point clouds representing the 3D core piece models, we rotated each slice’s points randomly around the cylinder axis. We then took the slices of 1 mm thickness from the newly aligned models and analysed via ellipse fitting d_max and d_min. Because the generated point clouds represent perfectly circular cylinders, the difference between d_max and d_min (Δd) should be zero. Thus, any non-zero Δd value indicates the “error” introduced by the tilt of the cylinder. If Δd is zero, or at least significantly lower than the expected radial deformation of the core samples, the methodologies can be used to calculate differential stress, ∆S (Sect. 3.2.3). The orientation results of the test revealed a slight tilt of the cylinder axes that led to a Δd of at most 1–2 μm, and in the best cases it was less than 1 μm. The error introduced by the tilt are thus 1–2 orders of magnitudes smaller than the expected deformations of many tens to few hundred μm. The manual alignment method produced results that were as accurate as the automated routine or better. Because of this, all analyses of photogrammetric models were performed using the visual method and the minor effect of the tilt was neglected. Finally, Δd and the orientation of d_max were obtained for each core piece, together with their standard deviations as described in Sect. 3.2.1. Circular statistics (Mardia and Jupp 2000) were used to compute mean orientation and standard deviation.

For better comparison of the CMM and photogrammetric data sets, we analysed 1 mm thick slices of the photogrammetric 3D core models and projected the mesh points along the model’s cylinder axis onto a common x–y-plane (i.e., collapsing the points to obtain a 2D data set from which the shape is determined using ellipse fitting). Note that varying the slice thickness between 0.01 and 10 mm had negligible overall effects on the resulting values of Δd and the direction of d_max. The differences were < 3 μm and < 2°, respectively. To account for the presence of fractures and other surface abnormalities (note that these cause locally smaller core diameters), we applied a filter to the calculated values of Δd. Because the expected diametrical deformation of the investigated core specimen is 50–150 μm, any value greater than 500 μm was discarded as an outlier and was not used for the analyses. Excluding slices with Δd > 300 μm and Δd < 50 μm was also tested but produced negligible differences and was not considered further.

3.2.3 Calculation of Stress Difference from Core Geometry

When a rock core is removed from the rock mass during the drilling process and transferred from its in situ, compressive stress state to an unconfined state (i.e., atmospheric pressure), unloading causes expansion of the core. Assuming isotropic, elastic material behaviour and an originally circular core cross-section, the Diametrical Core Deformation Analyses (DCDA), i.e., analysing the differences in core diameter, can be used to estimate the stress difference normal to the drill core axis. In case of a vertical borehole, the direction of the maximum core diameter, d_max, is in the direction of S_Hmax (see Fig. 1b).

We used Eq. 1 given by Funato et al. (2012) to calculate the differential stress, ∆S. Following Funato et al. (2012), we approximated the initial core diameter, d₀, which cannot be measured, with the minimum core diameter, d_min, which is not strictly correct but has a negligible impact on the estimate of differential stress (note that Δd is about three orders of magnitude smaller than d₀ in our case). The solution assumes a linear elastic and isotropic material behaviour, i.e., neglecting possible anelastic and anisotropic deformations:

$$\Delta S = S_{\max } - S_{\min } = \frac{{d_{\max } - d_{\min } }}{{d_{0} }}\, \cdot \,\frac{E}{1 + \nu } \approx \frac{{\overline{\Delta d} }}{{d_{\min } }}\, \cdot \,\frac{E}{1 + \nu }$$

(1)

E and v are the Young’s modulus and the Poisson's ratio, and $\overline{\Delta d }$ is the average of the diametrical differences (note that using 1-mm-thick core slices we calculated many values of ∆d per core piece). In addition, we calculated the average direction of d_max per core piece. We calculated ∆S for E = 65 GPa, following Valley and Evans (2019), and assumed ν = 0.22 (Braun 2007). To assess the dependency of the differential stress estimate on the parameters of Eq. 1 we conducted a simple sensitivity analysis (Sect. 4.1). Furthermore, we explored possible effects of rock anisotropy (Sect. 4.3) on the core’s diameter using numerical simulations (Sect. 4.5).

3.3 Core Discing

We analysed rock core discing to estimate the directions of S_Hmax and S_hmin based on the geometry of the core disc fractures. The saddle trough axis (i.e., concave axis of the disc; e.g., Haimson and Lee 1995; Fig. 1a) gives the direction of S_Hmax. We used unrolled 360° core photos with a resolution of 10 pixels/mm and unrolled, shaded, photogrammetric models by Gretillat (2017) to map the traces of discing fractures. The fracture traces were readily seen in the data sets due to their brighter colour compared to the surrounding rock (possibly caused by drilling mud and high microcrack density) and aperture, which led to slight depression in the core surface. The mapped fracture traces were digitised and used for identifying the locations of fracture trace high and low points. The line connecting the two low points (i.e., trough axis) gives the S_Hmax orientation. We grouped the saddle-shaped disc fractures into two classes of quality; fractures of high quality are well visible, have continuous traces along 360° of the core circumference, and each two distinctive high and low points. Also, fractures of lower quality have continuous traces along 360°, but are more difficult to identify and/or have a poorly-developed saddle-shape. Flat disc fracture traces, i.e., without saddle shape, were rare (< 2% of all identified traces) and excluded from further analyses, same as induced fractures with incomplete traces. For each core piece, all azimuths relative to the reference line of the high and low point directions were averaged using directional statistics to determine a mean value and the 1σ standard deviation. In addition, the thickness of the core discs was measured. In total, 106 saddle-shaped disc fracture traces across 16 pieces were mapped.

3.4 Radial Ultrasonic Measurements

We measured ultrasonic, compressional (p-wave) velocities in the cores’ radial directions to characterise their radial anisotropy. Ultrasonic tests were carried out with a Proceq Pundit Lab Plus© device and the data processed with PunditLink© software. A 54 kHz sender and receiver pair was used at 500 V and the signals amplified by 500 times. We set up the sensors diametrically, i.e., sender and receiver were about 101 mm apart, and no couplant was necessary given the very smooth core surface and conically shaped acoustic transducers. The tests were completed on 22 core pieces with ten measurements per position, with an angular resolution of 15° starting from the reference line (0°) to 180° (Fig. 4a), and at 1 cm intervals along the core. In total, 280 slices were measured across these 22 core pieces, for a total of 3360 velocity values (12 per slice, excluding a check value carried out at the 180° position). The onsets of the p-waves were automatically identified by the PunditLink© software, and manually corrected where necessary. Finally, we calculated the mean value for each recording position, the mean value for each azimuthal position along the core piece, and identified the minimum and maximum velocity directions per core piece. Piece lengths, measured along the reference line, ranged from 4.3 to 36.5 cm, with an average length of about 17 cm. Only core pieces without larger aperture (1–2 mm) discing fractures were used and the core ends (1–2 cm distance) were excluded from testing.

In addition, we analysed the orientation of rock foliation by optically estimating the alignment of elongated feldspar phenocrystals, and hornblende and biotite crystals (Sect. 2.2). Structure analysis was conducted on larger, well aligned core pieces only (4-1, 4-2, 5-1, 5-2, 6-1 to 6-7, 7-1, and 10-2; Fig. 3).

3.5 Numerical Simulation

We used the three-dimensional finite element code RS3 from Rocscience to investigate effects of transverse isotropy. Our model geometry consists of a 2 × 2 × 5 m block penetrated by a borehole with a diameter of 212.7 mm on the top 3 m of the block (see Sect. 2.1). A 101 mm core is preserved in the centre of the borehole. The geometry was meshed with second-order tetrahedral (10-noded) elements. A graded mesh approach was used with mesh refinement in a volume along the core and borehole that will be used for our analyses. Roller boundary conditions (zero displacement in the direction perpendicular to the model faces) were applied to the external model boundaries. Initial stress conditions are taken from Table 2 with S_v = 122 MPa, S_Hmax = 115 MPa, and S_hmin = 76 MPa. The S_Hmax magnitude stems from the best estimate by Valley and Evans (2019) but is less reliably constrained (see Sect. 2.4).

The model is run in two stages. In the first stage, the model is a full solid block, including the annulus space between the core and the wellbore wall. In the second stage, the annulus is excavated at once. When excavation occurs, the roller boundary conditions on the top of the core are removed to allow the core to fully relax.

Core diameter and core diameter changes in the model were evaluated using the following procedure. Due to model discretisation, diameters and ellipticity could not be readily determined on the model. Instead, we first selected the nodes on the core external boundary over a small slice of 2 mm located in the centre of our refined mesh volume. We project these nodes on the x–y plane and find the best fitting ellipse through the data using the direct least fitting approach from Halíř and Flusser (1998). The small and large axis of the ellipse are then our estimates of the core diameters and allow us to estimate core ellipticity.

4 Results

4.1 Diametrical Core Deformation Analysis

Table 4 shows the results of ∆d magnitudes, d_max orientations, and the calculated values of ∆S for the 30 photogrammetrically scanned core pieces. Note that most core pieces could not be aligned with the adjacent core pieces (Fig. 3) and that the lengths of the pieces and, thus, the number of 1-mm thin slices for the DCDA analysis per core piece varies considerably. Several pieces are single core discs, particularly from core trays 1 and 9, so that the data is based on very few slices (< 10). The magnitude of ∆S was calculated using Eq. 1.

Table 4 DCDA results of photogrammetric (N = 30) and CMM (N = 4) measurements. The latter data are given in italic

The one standard deviation (1σ) values of the orientations do not differ between the different lithologies and their median value is 27°. Thus, the inferred variability of S_Hmax orientation is an order of magnitude higher than the variability derived from the borehole breakouts along the wellbore length from which the core pieces were taken (± 4°). The adjacent core pieces 5-3 and 5-4 as well as 6-2 to 6-5 could be aligned well and show that the orientations of d_max are similar (168 ± 20° and 168 ± 27° for pieces 5-2 and 5-3 and ranging between 131 ± 18° and 155 ± 31° for pieces 6-3 to 6-7). The median value of Δd is 101 μm. Note that we excluded six outliers in the data set of Δd (marked with an asterisk symbol in Table 4) using box plot analysis (not shown). The outliers have extraordinarily high values of Δd and are mostly from core box 1, which showed many separate discs compared to the nondetached discs (elsewhere referred to as ‘incipient discs’) as found in the remaining core boxes. Finally, we received differential stresses, ∆S, with a median value of 53 MPa for E = 65 GPa and ν = 0.22. Core pieces of monzonitic and monzogranitic composition have about similar ∆S values. The ∆S results of individual core pieces have a large spread because the core pieces yielded a large uncertainty in Δd.

The dependencies of the differential stress estimate on the parameters of Eq. 1 are straightforward. Overestimation of E and Δd lead to overestimation of ∆S (direct dependency) and an overestimation of ν and d₀ lead to an underestimation of ∆S (inverse dependency). Let us assume base case parameters E = 65 GPa, ν = 0.22, d₀ = 101 mm, and Δd = 101 μm. This base case is inspired by the parameters expected for the Basel well (Table 1) and using the median value of Δd received from diametrical measurements of cores from boxes 2 to 10 (Table 4). Let’s also assume realistic ranges for the parameters. The typical uncertainty for the elastic parameters, E and ν, is 20%. The core diameter difference can be estimated with an accuracy of 10 µm (~ 10%). The initial core diameter may likely vary within 0.5 mm (~ 0.5%) and will be neglected in the analysis. These estimations lead to an uncertainty of -31% (∆S = 36.8 MPa; low case) and + 38% (∆S = 73.3 MPa; high case) on the stress difference. Fig. 6 illustrates the contribution of each parameter to the uncertainty estimation of the differential stress. A significant contribution arises from the uncertainty on the Young's modulus.

Fig. 6

Sensitivity of differential stress estimates (∆S) inferred from DCDA. The black dot marks the base case scenario

Figure 7 compares the results of the DCDA analysis of core pieces 4-1, 5-2, 6-4, and 7-1 using the photogrammetric technique (red) with the results received using the CMM technique (blue). The data sets include an about similar number (n) of analysed slices. The comparison is based on the magnitude of Δd and the direction of d_max of 1-mm thick slices, i.e., each point on the polar scatter plot represents one core slice. We plotted the points from the reference line (0°) to 180° and mirrored them to provide a better overall impression of the circumferential shapes apparent in the results. The CMM and photogrammetric analyses comprise very similar diametrical shapes of the four pieces. However, they are not exactly the same; the CMM data set shows less dispersed orientations of d_max. In addition, piece 6–4 exhibits few slices with up to about 200 μm larger Δd values in the photogrammetric data set than obtained in the CMM analysis. Nevertheless, the differences in average magnitudes of Δd range between 2 and 11 μm (Table 4), which is well within the assumed accuracy of the photogrammetric scanner (Sect. 3.2.2). Figure 8 presents the angular differences of the mean direction of d_max for different magnitudes of Δd between the CMM and photogrammetric techniques. The difference in mean azimuth of d_max, considering all Δd values, range between 2 and 9° and decrease to < 4° when considering values of Δd > 200 μm.

Fig. 7

Comparison of DCDA results (magnitude of ∆r, direction of d_max) of a the CMM technique (blue) and b the photogrammetric approach (red) for core pieces 4–1, 5–2, 6–4, and 7–1 (not aligned with each other). Note that each point represents a 1-mm core slice. For easier visual interpretation we mirrored the data points and, thus, displayed the differences in core slice radii, ∆r = ∆d/2, instead of ∆d

Fig. 8

Angular differences of mean d_max directions between CMM and photogrammetric results of DCDA at different magnitudes of ∆d. Overall, angular differences are ≤ 11°, and reduce to few degrees when considering larger magnitudes of ∆d

4.2 Core Discing

Figure 9a shows an example of an unrolled 360° optical core circumference image of pieces 6-1 and 6-2. Bright traces mark embedded core fractures. Figure 9b presents the mapped traces of discing fractures (black, numbered), fracture low and high points, and secondary fractures (grey) of the two pieces. The origin of the latter is not well understood.

Fig. 9

Example of a an unrolled 360° core surface image and b mapped non-detached disc fracture traces (black lines) describing saddle-shaped fracture geometries with disc low points (black dots) and high points (white dots)

In total, 106 disc fracture traces were mapped on 16 longer core pieces and 90% of these were classified as high quality, the remaining 10% are of low quality (see Sect. 3.3). The mean spacing of disc fractures ranges between about 2 cm and 4 cm and is 2.7 ± 0.08 cm on average but we recall here that most discs are not fully separated and represent partial discing. Taking the classification proposed by Lim and Martin (2010) our data would fall in the category “medium disking” or “partial disking”, implying a maximum principal stress to tensile strength ratio from 6 to 8. For our estimated tensile strength ranging from 4 to 11 MPa (Table 1) this leads to maximum stress (Smax) estimation ranging from 24 to 88 MPa.

All disc fractures comprise a saddle-shaped geometry that can be used to estimate S_Hmax and S_hmin orientations, using the low and high saddle points, respectively. The orientations of S_Hmax and S_hmin with respect to the reference line are summarised in Table 5. The orientation variability (i.e., 1σ) per piece ranges between 1° and 9° (mean 3.8°) for the orientation of S_Hmax and between 0° and 6° (mean 3.0°) for the orientation of S_hmin. The angle between S_Hmax and S_hmin is 84.2° on average, which suggests that the borehole axis is not (perfectly) parallel to a principal stress direction (or the vertical stress) (see, e.g., Dyke 1989 and Röckel 1996). Note that the BS-1 borehole is about 7.5° off from vertical in the cored section (Fig. 2b). Assuming a similar orientation of S_Hmax along the entire cored depth and considering the orientation variability within single pieces, the absolute orientation values given in Table 5 suggest that some pieces (5-2 to 6-2, 6-3 to 6-7, and 7-1 to 7-2) are well aligned, while others (e.g., 4-1 to 4-2 and 7-2 to 7-4) are not.

Table 5 Directions of S_hmin and S_Hmax with respect to the reference line inferred from the shape of the core discing fractures. ∆ gives the smaller, mean angle between the axes defined by low and high points. Note that not all pieces are aligned with each other

4.3 Diametrical P-Wave Velocities

Figure 10 shows the magnitudes of v_pmax and v_pmin of 22 core pieces (i.e., 280 core slices). V_pmax and v_pmin are on average 4753 ± 149 m/s and 4171 ± 413 m/s, respectively. The absolute velocity values are within the expected values for granitic rocks (about 4–6 m/s; e.g., Bourbié et al. 1987; Christensen 1989, and references cited therein). The angles between v_pmax and v_pmin are 90 ± 12°. Differences between v_pmax and v_pmin range between 310 and 820 m/s for all pieces. The overall ratio of v_pmax to v_pmin is 1.13 ± 0.04. This difference indicates a clear rock anisotropy. No significant differences of the velocity magnitudes and structure between monzogranite, monzonite, and mafic enclaves were found.

Fig. 10

Histograms of the magnitudes of a maximum and b minimum radial compressional wave velocities of all measured pieces and slices. The bin widths are 0.1 km/s

V_pmax and v_pmin orientations do not coincide with d_max or d_min (and disc fracture trough and high point) orientations (Fig. 11). V_pmax and d_max enclose angles of 57 ± 18°, while they are 47 ± 21° between v_pmax and disc fracture trough orientations. However, there exists a clear relationship between the velocity structure and rock structural anisotropy. The angle between the strike of the rock anisotropy plane and v_pmax ranges between − 20° and + 20° (average 2 ± 16°; compare blue and black indicators in Fig. 11). The dip of the rock foliation with respect to the core axis ranges between 73° and 84° (average 78 ± 4°).

Fig. 11

Comparison of S_Hmax orientations derived from DCDA (grey) using the photogrammetric approach (Sect. 3.2.2) and from analysis of core disc low points (red; Table 5). Note that the orientations of S_Hmax are given with respect to S_Hmax inferred from disc fracture shape set to 0°. Aligned core pieces are marked with green boxes. Blue indicates the orientation of vpmax (note that for pieces 3–2 and 6–1 no velocity data were acquired). Finally, black markers indicate the strike of the rock structural anisotropy plane where measured

4.4 Comparison of S _Hmax Directions Inferred from DCDA and Disc Fracture Geometry

Figure 11 compares per core piece the orientations of S_Hmax from DCDA and inferred from the geometric analysis of the core discs (i.e., the axis orientation defined by the low points of the saddle-shaped core discs). The angular differences range between 2° and 32° (mean 15.5°). It can clearly be seen that the 1σ-uncertainty ranges of S_Hmax orientations overlap considerably in the two data sets and that uncertainties inferred from DCDA are about one order larger than those of the disc shape analysis.

4.5 Evaluation of the Impact of Transverse Isotropy

Since our p-wave velocity measurements indicate some petrophysical anisotropy of the Basel monzogranite, we decided to use the numerical model presented in Sect. 3.5 to evaluate the impact of transverse isotropy on the evaluation of the differential stress based on the DCDA method. We do not propose here a systematic parameter analysis on all parameters but focus on a base case reproducing the conditions encountered by our Basel core, with the geometry, as well as boundary and initial conditions described in Sect. 3.5. With these conditions, the ∆S is equal to 39 MPa. For the elastic properties listed in Table 1 and assuming isotropic conditions, the core diameter difference computed using Eq. 1 is 74 µm.

To fully parametrise a transverse isotropic material, five independent elastic parameters are required: two Young’s moduli (E_x = E_y, E_z), two Poisson’s ratios (ν_xz = ν_yz, ν_xy), and the shear modulus (G_xz = G_yz). The x–y directions define the isotropy plane while the z-direction is perpendicular to it. For the sake of our analyses, we reduced the number of parameters by assuming the following simplifications:

• 1. We used the Saint–Venant simplification to express G_xz in terms of the other parameters using the following relationship: $G_{xz} = \frac{{E_{x} E_{z} }}{{E_{x} \left( {1 + 2\nu_{xz} } \right) + E_{z} }}.$

• 2. We used a single identical value of 0.22 for all Poisson’s ratios.

• 3. We expressed E_z as a function of E_x using the anisotropy index λ: E_z = λE_x.

In a first analysis we assess the general impact of anisotropy and isotropy plane orientation on the diametrical core deformation. Using the simplifications above, we can thus fully describe our transverse isotropic material model by defining the orientation of the isotropy plane relative to our vertical borehole and the anisotropy index. To produce results directly comparable to the possible behaviour of the Basel core, we used a dip angle for the isotropy plane of 78° based on observations of mineral alignment on the core samples. The dip direction is however unknown (our core is not oriented) and we used values spanning across all possible situations, from dipping toward S_Hmax to dipping toward S_hmin. The results of these analyses are presented in Fig. 12 in terms of computed core diameter differences. For isotropic models (λ = 1), all models are consistent and agree with the analytical solution of Eq. 1, i.e., the modelled conditions produce a core diameter difference of 74 µm. When the isotropy plane is almost perpendicular to S_Hmax (red case, 090/78 in Fig. 12; note that we set S_hmin arbitrarily to strike N–S), the effect of stress and stiffness anisotropy sums up generating larger core diameter differences. The opposite effect takes place when the isotropy plane is quasi perpendicular to S_hmin (blue case, 000/78 in Fig. 12) with both effects compensating themselves leading to a smaller core diameter difference. It is quite clear that the effect of material transverse isotropy is significant on the deformation of the core and should not be neglected in the core deformation analyses.

Fig. 12

Numerically simulated impact of isotropy plane orientation and anisotropy index (λ) on core diameter differences (∆d). Note that we set S_hmin arbitrarily to strike N–S

In a second set of analyses, we reduce our parametric space based on the consideration exposed in the following to compare more directly our modelling output with our core diameter deformation measurements. We put bounds on the most critical parameters. For the stress magnitude, the most uncertain one is the S_Hmax magnitude that can range at the depth of interest between 106 to 160 MPa (see Table 2), which implies a ∆S of 30 to 84 MPa. The other very uncertain parameter is the anisotropy index, λ, and the isotropy plane orientation. For λ, we considered the measured range of p-wave velocity and derived from it an anisotropy index for the dynamic Young’s moduli that we considered representative for static moduli anisotropy. This leads us to consider λ ranging from 0.59 to 0.99 with an average value of 0.77. For the isotropy plane dip, we consider the range of observed mineral fabric varying from 73° to 84°. For the azimuth we used the indication given by the angular difference between the direction of v_pmax (typically aligned with the strike of the mineral fabric) and the disc low points (considered as representative of S_Hmax direction). This leads us to consider isotropy plane azimuth ranging from 026° to 068° (average 047°) where S_Hmax direction in our simulation is arbitrarily set to W-E direction and S_hmin to N–S direction.

Using these reasonable bounds on our parameters, we simulated the range of expected core diameter differences ∆d (Fig. 13b) and compared them with the measured ∆d (Fig. 13a). We find that the simulated and observed ranges are very consistent except for the first core pieces (pieces 1-1 to 2-4) and some outliers (pieces 3-2 and 6-5). We hypothesise that at least some of these specific outliers may be caused by more damage (pieces 1-1 to 1–22 and 3-2 are more heavily disced, piece 2-4 seemed affected by a steep drilling induced fracture; Fig. 3) and, thus, the assumption of purely elastic deformation may not be fulfilled.

Fig. 13

Comparison between a measured and b modelled core diametrical differences (∆d). Note that we set S_hmin arbitrarily to strike N-S

5 Discussion

5.1 High Spatial Resolution Estimation of Core Diametrical Geometry Using Photogrammetry

To date, precise measurements of rock core diameters on the order of micrometres are carried out, e.g., by the optical micrometre developed by Funato and Chen (2005) using Keyence LS-7000 series digital micrometre sensors. Intact core pieces of few decimetre lengths are selected and their diameter is measured at a few distances along the core. The diametrical accuracy is about 1–3 μm and the azimuthal resolution is set to few degrees depending on core rotation speed. A least square regression is used to fit a sinusoidal curve to the average data acquired at different core piece depths (e.g., Ito et al. 2013). The technique yields high-precision diametrical data at few instances along intact core pieces (low spatial resolution). In this research, we explored an unconventional technique, i.e., photogrammetric scanning, to record core geometry at high spatial resolution. Indeed, compared to the optical micrometre, the photogrammetric approach acquires millions of measurement points from different viewing angles (i.e., one point cloud per view) that are used to calculate the object’s (i.e., core’s) surface geometry with an accuracy of about 10–20 μm (Sect. 3.2.2). To assess the geometric quality of core diametrical shape inferred from this new technique we measured four core pieces with a coordinate measuring machine (CMM) with an accuracy of about 1 μm; Section 3.2.1; Fig. 7). The cores that we used in this study originate from the 5 km deep Basel-1 borehole (Häring et al. 2008; Ziegler et al. 2015; Fig. 2). The orientations of the maximum core diameters were assumed to follow the longer axes of fitted ellipsoids to the photogrammetric and CMM data sets. The angular differences between photogrammetrically derived and CMM core diameter orientations range between 2 and 9° when considering all data (Fig. 8). Thus, the angular differences are small and well within the individual orientational variability of few tens of degrees (Table 4). Likewise, the measured values of ∆d are similar, i.e., they differ by 2–12 μm (2–10%), which is within the assumed error of the photogrammetric scanner and our analysis routine. Thus, the photogrammetric technique proved to be adequate for performing DCDA in a quasi-continuous manner over the core length (high spatial-resolution). Omitting antireflection coating of the core pieces, which may be difficult to apply with homogenous thickness onto the core specimen (Sect. 3.2.2), and selecting specific photogrammetric scanners for the core sample size are possible improvements for the accuracy of photogrammetric data acquisition.

5.2 Stress Orientation Estimation

Using the Basel-1 core, our ability to estimate the stress orientation from core indicators is limited because the Basel-1 core is not oriented. However, we can explore the relative consistency between independent estimators. One source of information is the occurrence of embedded core discing fractures identified on core images and photogrammetric data (Fig. 5b). Analysis of the mostly saddle-shaped disc fractures revealed consistent S_Hmax orientations of aligned core pieces, and a low variability of on average 4°. In the depth interval between 4909 and 4917 m, where coring took place, stress-induced borehole breakouts occur on opposite sides of the borehole. Valley and Evans (2015) identified borehole breakout orientations systematically for every 0.4 m in the given depth interval (i.e., 46 data points). The breakouts occurred at 51.7 ± 3.3° and 232.8 ± 4.1° clockwise from North. The orientation variability of S_Hmax derived from borehole breakouts is essentially the same as for S_Hmax inferred from disc fractures. Assuming that S_Hmax orientation does not vary considerably over the cored section, which is supported by borehole breakout analysis results along this section, we used the disc fracture geometry as a new reference instead of our initial, arbitrary reference line (see Sect. 3.3). Considering the 1σ-variability in S_Hmax orientations derived from the DCDA analysis of on average ± 27°, we find a good agreement between the S_Hmax orientations of the DCDA and disc fracture analyses. The two independent methods yield angular differences in S_Hmax below 22.5° for 13 out of 16 core pieces (Fig. 11). It is worth to note that mapping induced facture traces of the Basel-1 core yielded prime discing fractures and secondary fractures. The secondary fractures form partial traces of mostly < 180° of the core circumference (marked as grey dots in Fig. 9b), locating often between the low points of the disc fractures. Their appearance is frequent but not as systematic as the saddle-shaped discing fractures. The origin of these secondary induced fractures is unclear.

5.3 Stress Magnitude Estimation

Our analyses provide two new independent estimates for the S_Hmax magnitude stemming from DCDA and core disk thickness to diameter ratio. For DCDA, using our best-case estimates for mechanical properties and assuming linear elastic and isotropic material behaviour, the inferred median ∆S value using DCDA with ∆d measurements on Basel-1 core pieces was 53 MPa, which is within the uncertainty range derived from other stress estimation techniques at the Basel deep borehole. However, we recognise that this estimate can be affected by various effects, including elastic anisotropy and non-elastic behaviour. Our assessment of transversal isotropy on ∆S results showed that rock anisotropy must be considered to obtain reasonable stress estimates (Fig. 12). The comparison between measured and simulated diameter differences, considering rock anisotropy, are coherent except for a few pieces (Fig. 13). This indicates that in the case of the granitic core of Basel-1, anelastic deformation in the radial direction is not dominant even after core storage for more than ten years. This suggests that outside the process zones of brittle fracturing the rock behaves primarily in an elastic manner and that time-dependent effects are relatively small compared to the given uncertainties of Δd. This is consistent with results by Lim et al. (2012) who found that stress-induced transgranular microcracks in Lac du Bonnet granite “formed in a plane perpendicular to the core axis”, i.e., they are not greatly affecting radial strains. This is valid for our low porosity crystalline rock cores, but unlikely to be generalised to other lithologies.

In our situation, the usefulness of the DCDA analyses for better constraining the stress magnitudes, particularly the magnitude of S_Hmax, is limited largely because of the large uncertainty in our estimate of the elastic modulus and elastic anisotropy. This is a limitation of our study, but this is not a limitation of the method. Indeed, elastic moduli and anisotropy could be measured on core plugs. We did not perform such analyses yet because our investigations were limited to non-destructive methods, but this is something subject to further studies. Another limitation for the estimation of the stress magnitude is the large variability observed in the diametrical difference value (Table 4). We believe that this variability is inherent to the method because the measurements are taken at the grain scale and most rock type are very heterogeneous at this scale. This limitation applies to all stress measurement techniques that are taking place at a small scale as for example strain measurements during rock overcoring (Sjöberg et al. 2003). Combining numerous measurements is the typical approach for averaging out the variability, but such an approach is not satisfying when only a limited number of measurements are available as this is for example typically the case for the overcoring technique. The data processing for the DCDA approach based on photogrammetric scanning could be largely automatised making averaging possible for upscaling the stress measurements (Martin et al. 1990). If applied massively on continuous cores, it would permit to derive continuous stress profiles, an opportunity not readily available for most stress measurement techniques.

Analysis of the core disc thickness/diameter ratio led to an estimate of S_max ranging between 24 and 88 MPa based on the empirical relationship derived by Lim and Martin (2010). This is significantly lower than the estimates from other stress indicators. The lower range, which stems from a low 4 MPa tensile strength estimate, is certainly too low as it would imply magnitudes lower than S_hmin. However, the stress estimate from the disc shape is directly dependent on the tensile strength estimate. Where measurements are available, the estimate of tensile strength can vary quite widely due to the presence of heterogeneities and micro-defects leading to the initiation and propagation of unstable tensile fractures. An order of magnitude variability, from the order of 1 MPa in a test strongly influenced by heterogeneities to the order of 10 MPa or more in more homogeneous specimens, is not uncommon and will have a direct influence on the stress magnitude estimation. In our situation, the tensile strength is weakly constrained by only indirect considerations. On the other hand, assuming that the in situ stress magnitude of S_max is equal to S_v (122 MPa) and that the observed ratio of disc thickness to disc diameter is 0.27, would imply a tensile strength of 15–20 MPa, which would be unusually high for the tensile strength of coarse-grained crystalline rocks reported in the literature (e.g., Perras and Diederichs, 2014). Thus, another possible explanation for the observed discrepancies is that the relationship by Lim and Martin (2010) is not valid in our situation. This could be due to the difference in core diameter. Their study is based on a core diameter of 45 mm whereas our cores are 101 mm. This could explain why we observe less discing as the relationship by Lim and Martin (2010) predicts. Another explanation is that the relationship neglects the influence of the magnitude of the intermediate and minimum principal stresses. It is conceivable that the minimum and intermediate stress values have an influence, and that the stress conditions at Basel and at the AECL's URL, from which Lim and Martin's (2010) analyses were derived, differ. Other conditions between Basel and Manitoba’s URL, including thermal and fluid pressure conditions, clearly differ. Thus, effects including thermo-mechanical processes or the influence of fluid pressures could contribute to the observed discrepancies.

6 Conclusion

In this study we show that photogrammetric scan data of high-quality rock cores can be used to conduct Diametrical Core Deformation Analysis (DCDA). The photogrammetric method yields sufficient but about one order of magnitude lower accuracy than typical coordinate measurement machines (CMMs) or optical micrometres. Besides the diametrical data the photogrammetric technique captures core fracture traces, such as embedded stress-induced disc fracture traces, and the geometry of fracture surfaces at the ends of core pieces. As an example, we explored DCDA and core discing fractures of the 5 km deep Basel borehole. The photogrammetric technique produced consistent core geometry data compared to the results extracted from highly accurate CMM data. The differences in diametrical difference (∆d) between the two methods were between 2 and 11 μm and the angular differences of the inferred S_Hmax directions were between 2° and 9°. The Basel-1 core pieces are not oriented to North, which made our analysis complicated, and only few core pieces could be mated in six discontinuous groups of core pieces. Nevertheless, the piece-by-piece 1σ-variability of the orientation of S_Hmax based on core discing fractures was found to be about 4°, which is about the same for borehole breakout data from the same depth interval (4909‒4917 m). Finally, the consistent discing geometry could be used as a new core reference.

DCDA assumes that the rock core behaves perfectly linear elastic and isotropic (e.g., Funato et al. 2012). In our study we neglect possible radial anelastic strains, presuming most anelastic strain occurred axially and not radially as supported by core discing. Using the best estimate of available rock elastic modulus and Poisson’s ratio from the Basel core, we received a median horizontal stress differences, ∆S, of 53 MPa using the isotropic analytical solution. We explored the dependency of inferred horizontal stress difference on transverse isotropy. Some Basel rock core pieces showed a slightly anisotropic structure and vp, captured radially around the rock cores, revealed a systematic and clear maximum to minimum velocity ratio of on average 1.13. Our numerical analysis highlighted a strong effect of transverse isotropy, which may lead to substantial under- and overestimation of horizontal stress differences. Considering transverse rock isotropy and upper and lower bounds for maximum horizontal stress, rock isotropy plane orientation, anisotropy index, and elastic modulus, we simulated ∆d values ranging between 30 and 150 μm, which are similar to the measured 1σ-variability and consistent with a stress regime at the limit between normal and strike-slip. Our finding suggests that DCDA does not only require micrometre resolution data sets, but unless elastic moduli and their potential anisotropy are not locally and accurately estimated (e.g., using bi-axial loading tests) the output of the DCDA in terms of stress differences are highly uncertain.