The Stress Field in a Standardized Brazilian Disc: The Influence of the Loading Type Acting on the Actual Contact Length

Abstract

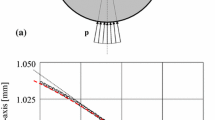
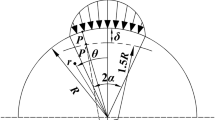
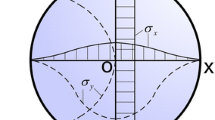
The aim of the present study was to determine the stress field developed in a Brazilian disc under conditions closely approaching those of the actual test executed according to the standardized procedure suggested by the International Society for Rock Mechanics. Advantage is taken of a recently introduced analytic solution for a mixed fundamental contact problem where the disc and the jaw are considered as a system of two interacting elastic bodies. Using the outcomes of that study, the complex potentials method is employed here for the solution of a first fundamental problem for a Brazilian disc under a parabolic load distribution. Analytic full-field formulae for the components of the stress field developed in the disc are given. The solution is then applied for the case of a disc made from Dionysos marble. The results are compared to existing ones obtained from solutions adopting statically equivalent loads either in the form of distributed (uniform or sinusoidally) radial pressure acting along the actual contact rim or in the form of diametrically acting point (line) loads. While the stress field in the major part of the disc seems to be rather insensitive to the exact load application mode, critical differences are detected in the vicinity of the loaded arc of the disc. The solution is assessed according to the results of a short series of Brazilian disc tests with PMMA specimens. The agreement between theoretical predictions and experimental data is satisfactory. Finally, it is indicated that, as opposed to previous solutions, the stress field (even at the disc’s center) is a non-linear function of the externally applied load depending, among others, indirectly on the properties of the disc’s and jaw’s materials, the combination of which dictates the extent of the contact angle.

Appendices

Appendix I

1.1 A Note on the Complex Potential in Case of Circular Load Distribution

Consider the circular distribution:

$$ P(\tau ) = \frac{1}{{3R_{1} K}}\sqrt {\ell^{2} - \tau^{2} } $$

Under the obvious simplifications: $\ell \approx \ell^{\prime } = R{ \sin }\omega_{\text{o}} ,\tau \approx \tau^{\prime } = R{ \cos }\vartheta$ (R = R ₁) becomes:

$$ P(\vartheta ) = \frac{1}{3K}\sqrt {{ \sin }^{2} \omega_{\text{o}} - { \cos }^{2} \vartheta } $$

Equivalently, since ${ \cos }\vartheta = \left( {s + \overline{s} } \right)/2$, it can be written as:

$$ P(s) = \frac{1}{3K}\sqrt {{ \sin }^{2} \omega_{\text{o}} - \frac{1}{2} - \frac{{s^{2} }}{4} - \frac{1}{{4s^{2} }}} ,\quad s = {\text{e}}^{{{\text{i}}\vartheta }} . $$

Therefore on the loaded rims (in the fictitious ζ-plane) it holds that:

$$ \sigma_{\rho \rho }^{ + } = - P(s) = - \frac{1}{3K}\sqrt {{ \sin }^{2} \omega_{\text{o}} - \frac{1}{2} - \frac{{s^{2} }}{4} - \frac{1}{{4s^{2} }}} . $$

Inserting the above value for $\sigma_{\rho \rho }^{ + }$ in the general formula:

$$ \Upphi (\zeta ) = \frac{1}{{2\pi {\text{i}}}}\int\limits_{\gamma } {\frac{{\sigma_{\rho \rho }^{ + } (s)}}{s - \zeta }} {\text{d}}s - \frac{1}{4\pi }\int\limits_{0}^{2\pi } {\sigma_{\rho \rho }^{ + } (\vartheta )} {\text{d}}\vartheta \quad \left( {{\text{Eq}}. \, 25} \right), $$

an integral appears of the form:

$$ \int {\frac{{\sqrt {C - s^{2} - \frac{1}{{s^{2} }}} }}{s - \zeta }} {\text{d}}s $$

A closed form solution for such an integral is not available.

Appendix II

2.1 An Alternative Load Distribution

Taking the squares of both sides of the second of Eqs. (14), for R ₁ = R, it follows that:

$$ P(\tau )^{2} + \left( {\frac{\tau }{3RK}} \right)^{2} = \left( {\frac{\ell }{3RK}} \right)^{2} , $$

which represents the equation of a circle of radius $\frac{\ell }{3RK}$.

A parabola (red color in the following figure) of the same area (demanded to insure static equivalence between the circular and the parabolic radial pressure distributions) that intersects the x-axis at the points $\mp \frac{\ell }{3RK}$ is described by the equation:

$$ P(\tau ) = \frac{\pi \ell }{8RK} - \frac{\pi }{8RK}\frac{\tau }{\ell }^{2} = \frac{\pi \ell }{8RK}\left[ {1 - \left( {\frac{\tau }{\ell }} \right)^{2} } \right]. $$

See Fig. 14.

Fig. 14

Cyclic versus parabolic pressure distribution