Skip to main content
SpringerLink
Log in

Generalized complex structures and Lie brackets

  • Published:
Bulletin of the Brazilian Mathematical Society, New Series Aims and scope Submit manuscript

Abstract

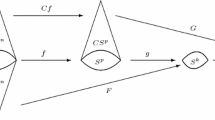
We remark that the equations underlying the notion of generalized complex structure have simple geometric meaning when passing to Lie algebroids/groupoids.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. M. Abouzaid and M. Boyarchenko. Local structure of generalized complex manifolds. J. Symplectic Geom., 4 (2006), 43–62.

    MATH  MathSciNet  Google Scholar 

  2. B. Anos. Monge-Ampère equations and generalized complex geometry — the twodimensional case. J. Geom. Phys., 57 (2007), 841–853.

    Article  MathSciNet  Google Scholar 

  3. H. Bursztyn, M. Crainic, A. Weinstein and C. Zhu. Integration of twisted Dirac brackets. Duke Math. J., 123 (2004), 549–607.

    Article  MATH  MathSciNet  Google Scholar 

  4. H. Bursztyn and O. Radko. Gauge equivalence of Dirac structures and symplectic groupoids. Ann. Inst. Fourier (Grenoble), 53 (2003), 309–337.

    Article  MATH  MathSciNet  Google Scholar 

  5. A. Cattaneo and G. Felder. Poisson sigma models and symplectic groupoids. In: “Quantization of singular symplectic quotients”, Progr. Math. 198, 61–93, Birkhäuser, Basel (2001).

    Chapter  Google Scholar 

  6. T. Courant. Dirac manifolds. Trans. Amer. Math. Soc., 319 (1990), 631–661.

    Article  MATH  MathSciNet  Google Scholar 

  7. M. Crainic and R. Fernandes. Integrability of Lie brackets. Ann. of Math., 157 (2003), 575–620.

    Article  MATH  MathSciNet  Google Scholar 

  8. M. Crainic and R. Fernandes. Integrability of Poisson brackets. J. of Differential Geometry, 66 (2004), 71–137.

    MATH  MathSciNet  Google Scholar 

  9. M. Gualtieri. Generalized complex geometry. Preprint math.DG/0404451, revised version: math/0703298.

  10. N. Hitchin. Generalized Calabi-Yau manifolds. Q.J. Math., 54 (2003), 281–308.

    Article  MATH  MathSciNet  Google Scholar 

  11. U. Lindstrom, R. Minasian, A. Tomasiello and M. Zabzine. Generalized complex manifolds and supersymmetry, to appear in Comm.Math.Phys, e-Print Archive: hep-th/0405085.

  12. Z.J. Liu, A. Weinstein and P. Xu. Manin triples for Lie bialgebroids. J. Differential Geom., 45 (1997), 547–574.

    MathSciNet  Google Scholar 

  13. K. Mackenzie and P. Xu. Lie bialgebroids and Poisson groupoids. Duke Math. J., 73 (1994), 415–452.

    Article  MATH  MathSciNet  Google Scholar 

  14. M. Stienon and P. Xu. Poisson quasi-Nijenhuis manifolds. Comm. Math. Phys., 270 (2007), 709–725.

    Article  MATH  MathSciNet  Google Scholar 

  15. R. Zucchini. A sigma model field theoretic realization of Hitchin’s generalized complex geometry. Preprint hep-th/0409181.

  16. A. Weinstein. Algébroides de Lie complexes sur les variétés réelles, mini-course (and private discussions) at l’Ecole Polytechnique, November (2004).

Download references

Author information

Authors and Affiliations

  1. Department of Mathematics, Utrecht University, P.O. Box 80.010, 3508 TA, Utrecht, The Netherlands

    Marius Crainic

Authors
  1. Marius Crainic
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Marius Crainic.

Additional information

Research supported by NWO (Vidi project no. 639.032.712).

About this article

Cite this article

Crainic, M. Generalized complex structures and Lie brackets. Bull Braz Math Soc, New Series 42, 559–578 (2011). https://doi.org/10.1007/s00574-011-0029-0

Download citation

  • Received:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00574-011-0029-0

Keywords

Mathematical subject classification

Search

Navigation