On the implementation of adaptive sliding mode robust controller in the stabilization of electrically actuated micro-tunable capacitor

Abstract

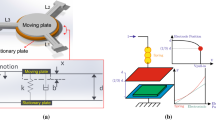
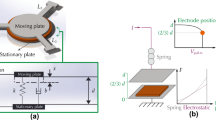
Parallel-plates based micro-tunable capacitors are known to have low travel ranges, which deteriorate as going even lower in terms of their initials gap sizes. Such conditions have put strict requirements on the operation of such designs and hence hindering their use in numerous practical applications requiring high tunability. This work is proposed to examine the possibility to implement a closed-loop control strategy to increase the maximum capacitance and therefore tunability of micro tunable capacitors. The suggested control strategy is implemented on an electrostatically actuated parallel-plates (one stationary and one movable) based micro-capacitor and had an objective to stabilize the movable electrode when it is close to the fixed one for the sake of maximizing its maximum capacitance and possibly improving its overall tunability. Robustness of the micro-capacitor to the so-called pull-in phenomenon (short-circuit instability) when using the closed loop control scheme is studied. Indeed, an adaptive sliding mode controller is designed to compensate the effects of uncertainty, disturbance and eliminate any possibility for chattering phenomenon. The controller proficiencies in terms of stabilizing the micro-capacitor and its robustness to uncertainty as well as disturbance have been thoroughly examined. Furthermore, the effects of the control parameters on the behavior of micro-capacitor, such as overshoot, settling time, steady state error, robustness to uncertainty, external disturbances and to the chattering phenomenon, have been completely inspected. The obtained results indicated satisfactory proficiency and trustworthiness of the proposed control strategy to achieve high level of tunability and maximum capacitance.

Appendix

1.1 Appendix A: Proof of the controller stability

If we consider a Lyapunov function described by the below expression:

$$ v = \frac{1}{2}\left[ {s^{2} + \left( {\alpha + \hat{\alpha }} \right)^{2} + \left( {\beta + \hat{\beta }} \right)^{2} + \mu^{2} + \theta^{2} } \right] $$

(10)

Its time derivative can therefore be written as follows:

$$ \dot{v} = s\dot{s} + \dot{\hat{\alpha }}\left( {\alpha + \hat{\alpha }} \right) + \dot{\hat{\beta }}\left( {\beta + \hat{\beta }} \right) + \mu \dot{\mu } + \theta \dot{\theta } $$

(11)

If we consider a sliding surface governed by the following state equation: $s = \dot{e}_{1} + k_{s} e_{1} = e_{2} + k_{s} e_{1}$, therefore for $\dot{s}$ the following relationship cab be also valid:

$$ \begin{aligned}\dot{s} & = \dot{e}_{2} + k_{s} \dot{e}_{1} = \dot{e}_{2} + k_{s} e_{2} \\ \dot{s}_{2} & = f\left( {x,t} \right) + g\left( {x,t} \right)u + d\left( t \right) + \Delta F\left( {x,t} \right) - \ddot{x}_{d} + k_{s} e_{2}\\ \end{aligned} $$

(12)

Substituting Eq. (12) into Eq. (11), we can write:

$$ \dot{v} = s\left[ {f\left( {x,t} \right) + g\left( {x,t} \right)u + d\left( t \right) + \Delta F\left( {x,t} \right) - \ddot{x}_{d} + k_{s} e_{2} } \right] + \dot{\hat{\alpha }}\left( {\alpha + \hat{\alpha }} \right) + \dot{\hat{\beta }}\left( {\beta + \hat{\beta }} \right) + \mu \dot{\mu } + \theta \dot{\theta } $$

(13)

Next, substituting the control law of Eq. (3) and the related relationship of $\dot{\hat{\alpha }}$, $\dot{\hat{\beta }}$, $\dot{\mu }$, and $\dot{\theta }$ into Eq. (13), the time derivative of the Lyapunov function $\dot{v}$ can be re-written as:

$$ \dot{v} = s\left[ { - \left( {\hat{\alpha } + \hat{\beta } + \mu } \right)\tanh \left( {\theta s} \right) + d\left( t \right) + \Delta F\left( {x,t} \right)} \right] - \left| s \right|\left( {\hat{\alpha } + \alpha } \right) - \left| s \right|\left( {\hat{\beta } + \beta } \right) - p\left| s \right|\left| {e_{1} } \right| - q\left| s \right|\left| {e_{1} } \right| $$

(14)

According to the assumed conditions: $\left| {\Delta F\left( {x,t} \right)} \right| \le \alpha$ and $\left| {d\left( t \right)} \right| \le \beta$, consequently the following conditions can also be verified: $s\Delta F\left( {x,t} \right) \le \left| s \right|\alpha$ and $sd\left( t \right) \le \left| s \right|\beta$.

Assuming the abovementioned relationships, the following inequality can be obtained for $\dot{v}$:

$$ \begin{aligned} \dot{v} & \le - \left( {\hat{\alpha } + \hat{\beta } + \mu } \right)s\tanh \left( {\theta s} \right) + \left| s \right|\beta + \left| s \right|\alpha - \left| s \right|\left( {\hat{\alpha } + \alpha } \right) \\ &\quad - \left| s \right|\left( {\hat{\beta } + \beta } \right) - \mu p\left| s \right|\left| {e_{1} } \right| - \theta q\left| s \right|\left| {e_{1} } \right| \\ \dot{v} & \le - \left( {\hat{\alpha } + \hat{\beta } + \mu } \right)s\tanh \left( {\theta s} \right) \\& \quad - \left| s \right|\left( {\hat{\alpha } + \hat{\beta } + \mu p\left| {e_{1} } \right| + \theta q\left| {e_{1} } \right|} \right) \\ \end{aligned} $$

(15)

Knowing that: $s\tanh \left( {\theta s} \right) = \left| s \right|\left| {\tanh \left( {\theta s} \right)} \right|$ (Aghababa and Akbari 2012), $\dot{v}$ can be finally re-written as follows:

$$ \dot{v} \le - \left| s \right|\left\{ {\left( {\hat{\alpha } + \hat{\beta }} \right)\left[ {\left| {\tanh \left( {\theta s} \right)} \right| + 1} \right] + \mu \left[ {\left| {\tanh \left( {\theta s} \right)} \right| + p\left| {e_{1} } \right|} \right] + \theta q\left| {e_{1} } \right|} \right\} $$

(16)

The term inside of brackets “{}” represents a positive number, and subsequently the condition $\dot{v} \le - \left| s \right|\left\{ \eta \right\}$ for the presented controller is therefore guaranteed, for which $\eta$ represents a positive number.