Skip to main content
SpringerLink
Log in

Stability analysis of restrained nanotubes placed in electromagnetic field

  • Technical Paper
  • Published:
Microsystem Technologies Aims and scope Submit manuscript

Abstract

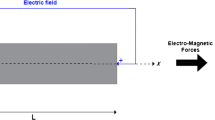
In this present work, buckling analysis of restrained nanotubes placed in electromagnetic field is studied on the basis of Euler–Bernoulli beam theory in conjunction with Eringen’s nonlocal elasticity theory. The modal displacement function is assumed for the stability analysis in order to discretize the derived governing equation. A Fourier sine series with Stoke’s transformation is utilized to investigate the buckling response. The essential advantage of this transformation is its ability of dealing with various boundary conditions to determine the buckling loads. For demonstrate the effects of various parameters such as Hartmann parameter, spring parameter and mode number on the stability response and critical buckling load of electromagnetic nanobeam a detailed study is presented. Variations of buckling loads, critical buckling loads and buckling load ratios of the nanobeam are exhibited with a number of tables and plotted figures. The results obtained from the analysis are discussed on the tables and figures.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14

Similar content being viewed by others

References

  • Aifantis EC (1999) Strain gradient interpretation of size effects. Int J Fract 95:299–314

    Google Scholar 

  • Akgöz B, Civalek Ö (2016) Bending analysis of embedded carbon nanotubes resting on an elastic foundation using strain gradient theory. Acta Astronaut 119:1–12

    Google Scholar 

  • Arda M (2018) vibration analysis of an axially loaded viscoelastic nanobeam. Int J Eng Appl Sci 10(3):252–263

    Google Scholar 

  • Arda M, Aydogdu M (2017) Buckling of eccentrically loaded carbon nanotubes. In: Bendikienė R, Juzėnas K (eds) Solid state phenomena, vol 267. Trans Tech Publications Ltd. pp 151–156

  • Arda M, Aydogdu M (2018) Longitudinal magnetic field effect on torsional vibration of carbon nanotubes. J Comput Appl Mech 49(2):304–313

    Google Scholar 

  • Arda M, Aydogdu M (2019a) Dynamic stability of harmonically excited nanobeams including axial inertia. J Vib Control 25(4):820–833

    MathSciNet  Google Scholar 

  • Arda M, Aydogdu M (2019b) Torsional dynamics of coaxial nanotubes with different lengths in viscoelastic medium. Microsyst Technol 25(10):3943–3957

    Google Scholar 

  • Arda M, Aydogdu M (2019c) Dynamic Analysis of a Viscoelastic Nanobeam. In: Karjust K, Kübarsepp J, Otto T, Hussainova I (eds) Key engineering materials, vol 799. Trans Tech Publications, pp 223–229

  • Avcar M (2014) Free vibration analysis of beams considering dif-ferent geometric characteristics and boundary conditions. System 4(2):2

    Google Scholar 

  • Chakraverty S, Jena SK (2018) Free vibration of single walled carbon nanotube resting on exponentially varying elastic foundation, curved layer. Structures 5:260–272

    Google Scholar 

  • Civalek Ö, Akgöz B (2010) Free vibration analysis of micro-tubules as cytoskeleton components: nonlocal Euler-Bernoulli beam modeling. Sci Iranica Trans B Mech Eng 17:367–375

    MATH  Google Scholar 

  • Civalek Ö, Demir Ç (2011) Bending analysis of microtubules using nonlocal Euler–Bernoulli beam theory. Appl Math Model 35:2053–2067

    MathSciNet  MATH  Google Scholar 

  • Civalek Ö, Demir C (2016) A simple mathematical model of microtubules surrounded by an elastic matrix by nonlocal finite element method. Appl Math Comput 289:335–352

    MathSciNet  MATH  Google Scholar 

  • Demir C, Civalek Ö (2013) Torsional and longitudinal frequency and wave response of microtubules based on the nonlocal continuum and nonlocal discrete models. Appl Math Modell 37(22):9355–9367

    MATH  Google Scholar 

  • Eltaher MA, Emam SA, Mahmoud FF (2013) Static and stability analysis of nonlocal functionally graded nanobeams. Compos Struct 96:82–88

    Google Scholar 

  • Eringen AC (1967) Theory of micropolar plates. J Appl Math Phys 18:12–30

    Google Scholar 

  • Eringen AC (1972) Nonlocal polar elastic continua. Int J Eng Sci 10:1–16

    MathSciNet  MATH  Google Scholar 

  • Eringen AC (1983) On differential equations of nonlocal elas-ticity and solutions of screw dislocation and surface waves. J Appl Phys 54:4703–4710

    Google Scholar 

  • Giunta G, Crisafulli D, Belouettar S, Carrera E (2011) Hierar-chical theories for the free vibration analysis of functionally graded beams. Compos Struct 94(1):68–74

    Google Scholar 

  • Gorgani HH, Adeli MM, Hosseini M (2019) Pull-in behavior of functionally graded micro/nano-beams for MEMS and NEMS switches. Microsyst Technol 25(8):3165–3173

    Google Scholar 

  • Gürses M, Akgöz B, Civalek Ö (2012) Mathematical model-ing of vibration problem of nano-sized annular sector plates using the nonlocal continuum theory via eight-node discrete singular convolution transformation. Appl Math Comput 219:3226–3240

    MathSciNet  MATH  Google Scholar 

  • Jena SK, Chakraverty S (2018a) Free vibration analysis of Euler-Bernoulli nanobeam using differential transform method. Int J Comput Mater Sci Eng 7:1850020

    Google Scholar 

  • Jena SK, Chakraverty S (2018b) Free vibration analysis of variable cross-section single layered graphene nano-ribbons (SLGNRs) using differential quadrature method. Front Built Environ 4:63

    Google Scholar 

  • Jena SK, Chakraverty S (2018c) Free vibration analysis of single walled carbon nanotube with exponentially varying stiffness, curved layer. Structures 5:201–212

    Google Scholar 

  • Jena RM, Chakraverty S (2019a) residual power series method for solving time-fractional model of vibration equa-tion of large membranes. J Appl Comput Mech 5:603–615

    Google Scholar 

  • Jena SK, Chakraverty S (2019b) Differential quadrature and differential transformation methods in buckling analysis of nanobeams, curved layer. Structures 6:68–76

    Google Scholar 

  • Jena SK, Chakraverty S (2019c) Dynamic behavior of an electromagnetic nanobeam using the Haar wavelet method and the higher-order Haar wavelet method. Eur Phys J Plus 134:538

    Google Scholar 

  • Jena SK, Chakraverty S, Jena RM, Tornabene F (2019a) A novel fractional nonlocal model and its application in buckling analysis of Euler-Bernoulli nanobeam. Mater Res Express 6:1–17

    Google Scholar 

  • Jena SK, Chakraverty S, Tornabene F (2019b) Vibration characteristics of nanobeam with exponentially varying flexural rigidity resting online early vary ingelastic foundation using differential quadrature method. Mater Res Express 6:1–13

    Google Scholar 

  • Jena SK, Chakraverty S, Tornabene F (2019c) Dynamical behavior of nanobeam embedded in constant, linear, parabolic and sinusoidal types of winkler elastic foundation using first-order nonlocal strain gradient model. Mater Res Express 6:0850f2

    Google Scholar 

  • Jena RM, Chakraverty S, Jena SK (2019d) Dynamic response analysis of fractionally damped beams subjected to external loads using homotopy analysis method. J Appl Comput Mech 5:355–366

    Google Scholar 

  • Jena SK, Chakraverty S, Tornabene F (2019e) Buckling behavior of nanobeams placed in electromagnetic field using shifted Chebyshev polynomials-based Rayleigh-Ritz method. Nanomaterials 9(1326):1–15

    Google Scholar 

  • Khalili SMR, Jafari AA, Eftekhari SA (2010) A mixed Ritz-DQ method for forced vibration of functionally graded beams carrying moving loads. Compos Struct 92(10):2497–2511

    Google Scholar 

  • Koiter WT (1964) Couple stresses in the theory of elasticity: I and II. Proc K Ned Akad Wet B Phys Sci 67:17–44

    MathSciNet  MATH  Google Scholar 

  • Lam DCC, Yang F, Chong ACM, Wang J, Tong P (2003) Experiments and theory in strain gradient elasticity. J Mech Phys Solids 51(8):1477–1508

    MATH  Google Scholar 

  • Li SR, Batra RC (2013) Relations between buckling loads of functionally graded Timoshenko and homogeneous Euler-Bernoulli beams. Compos Struct 95:5–9

    Google Scholar 

  • Lu P, Lee HP, Lu C, Zhang PQ (2006) Dynamic proper-ties of flexural beams using a nonlocal elasticity model. J Appl Phys 99:73510–73518

    Google Scholar 

  • Mercan K, Civalek Ö (2016a) Buckling analysis of silicon carbide nanotubes (SiCNTs). Int J Eng Appl Sci 8(2):101–108

    MathSciNet  Google Scholar 

  • Mercan K, Civalek Ö (2016b) DSC method for buckling analysis of boron nitride nanotube (BNNT) surrounded by an elastic matrix. Compos Struct 143:300–309

    Google Scholar 

  • Mercan K, Demir Ç, Akgöz B, Civalek Ö (2015) Coordi-nate transformation for sector and annular sector shaped graphene sheets on silicone matrix. Int J Eng Appl Sci 7(2):56–73

    Google Scholar 

  • Miandoab EM, Yousefi-Koma A, Pishkenari HN (2015) Nonlocal and strain gradient based model for electrostatically actuated silicon nano-beams. Microsyst Technol 21(2):457–464

    MATH  Google Scholar 

  • Mindlin RD (1963) Influence of couple-stresses on stress concen-trations. Exp Mech 3(1):1–7

    Google Scholar 

  • Mindlin RD (1965) Second gradient of strain, surface-tension in linear elasticity. Int J Solids Struct 1(4):417–438

    Google Scholar 

  • Mindlin RD, Tiersten HF (1962) Effects of couple-stresses in linear elasticity. Arch Ration Mech Anal 11:415–448

    MathSciNet  MATH  Google Scholar 

  • Murmu T, Pradhan SC (2009) Small-scale effect on the vibration of nonuniform nanocantilever based on nonlocal elasticity theory. Phys E 41:1451–1456

    Google Scholar 

  • Numanoğlu HM, Akgöz B, Civalek Ö (2018) On dynamic analysis of nanorods. Int J Eng Sci 130:33–50

    Google Scholar 

  • Rahmani O, Pedram O (2014) Analysis and modeling the size effect on vibration of functionally graded nanobeams based on nonlocal Timoshenko beam theory. Int J Eng Sci 77:55–70

    MathSciNet  MATH  Google Scholar 

  • Reddy JN, Pang SD (2008) Nonlocal continuum theories of beam for the analysis of carbon nanotubes. J Appl Phys 103:1–16

    Google Scholar 

  • Setoodeh AR, Khosrownejad M, Malekzadeh P (2011) Exact nonlocal solution for post buckling of single-walled carbon nanotubes. Phys E 43:1730–1737

    Google Scholar 

  • Thai HT (2012) A nonlocal beam theory for bending, buckling, and vibration of nanobeams. Int J Eng Sci 52:56–64

    MathSciNet  MATH  Google Scholar 

  • Toupin RA (1962) Elastic materials with couple-stresses. Arch Ration Mech Anal 11(1):385–414

    MathSciNet  MATH  Google Scholar 

  • Uzun B, Civalek Ö (2019a) Nonlocal FEM formulation for vibration analysis of nanowires on elastic matrix with different materials. Math Comput Appl 24(2):38

    MathSciNet  Google Scholar 

  • Uzun B, Civalek Ö (2019b) Free vibration analysis Silicon nanowires surrounded by elastic matrix by nonlocal finite element method. Adv Nano Res 7(2):99

    Google Scholar 

  • Uzun B, Yaylı MÖ (2020) Nonlocal vibration analysis of Ti-6Al-4V/ZrO2 functionally graded nanobeam on elastic matrix. Arab J Geosci 13(4):1–10

    Google Scholar 

  • Uzun B, Numanoglu HM, Civalek Ö (2018) Free vibration analysis of BNNT with different cross-Sections via non-local FEM. J of Comput Appl Mech 49(2):252–260

    Google Scholar 

  • Uzun B, Yaylı MÖ, Deliktaş B (2020) Free vibration of FG nanobeam using a finite-element method. Micro Nano Lett 15(1):35–40

    Google Scholar 

  • Wang CM, Kitipornchai S, Lim CW, Eisenberger M (2008) Beam bending solutions based on nonlocal Timoshenko beam theory. J Eng Mech 134:475–481

    Google Scholar 

  • Yang F, Chong ACM, Lam DCC, Tong P (2002) Couple stress based strain gradient theory for elasticity. Int J Solids Struct 39(10):2731–2743

    MATH  Google Scholar 

  • Yayli MÖ (2015a) Buckling analysis of a rotationally re-strained single walled carbon nanotube. Acta Phys Pol A 127(3):678–683

    Google Scholar 

  • Yayli MÖ (2015b) Stability analysis of gradient elastic microbeams with arbitrary boundary conditions. J Mech Sci Technol 29(8):3373–3380

    Google Scholar 

  • Yayli MÖ (2016a) Buckling analysis of a rotationally re-strained single walled carbon nanotube embedded ın an elastic medium using nonlocal elasticity. Int J Eng Appl Sci 8(2):40–50

    Google Scholar 

  • Yayli MÖ (2016b) An analytical solution for free vibrations of a cantilever nanobeam with a spring mass system. Int J Eng Appl Sci 7(4):10–18

    Google Scholar 

  • Zakaria M, Al Harthy AM (2017) Free vibration of pre-tensioned electromagnetic nanobeams, IOSR. J Math 13:47–55

    Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Civil Engineering, Faculty of Engineering, Bursa Uludag University, Görükle Campus, 16059, Bursa, Turkey

    Büşra Uzun, Uğur Kafkas & Mustafa Özgür Yaylı

Authors
  1. Büşra Uzun
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Uğur Kafkas
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Mustafa Özgür Yaylı
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Büşra Uzun.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Uzun, B., Kafkas, U. & Yaylı, M.Ö. Stability analysis of restrained nanotubes placed in electromagnetic field. Microsyst Technol 26, 3725–3736 (2020). https://doi.org/10.1007/s00542-020-04847-0

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00542-020-04847-0

Search

Navigation