Skip to main content
SpringerLink
Log in

Effect of rotation and gravity on the reflection of P-waves from thermo-magneto-microstretch medium in the context of three phase lag model with initial stress

  • Technical Paper
  • Published:
Microsystem Technologies Aims and scope Submit manuscript

Abstract

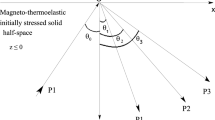
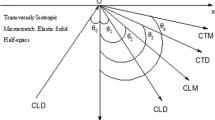
In this paper the linear theory of the thermoelasticity has been employed to study the effect the reflection of plane harmonic waves from a semi-infinite elastic solid under the effect of the magnetic field , rotation, initial stress and gravity. The medium under consideration is traction free, homogeneous, isotropic, as well as with three-phase-lag. The normal mode analysis is used to solve the resulting non-dimensional coupled equations. The expressions for the reflection coefficients, which are the relations of the amplitudes of the reflected waves to the amplitude of the incident waves, are obtained similarly, the reflection coefficient ratio variations with the angle of incident under different conditions are shown graphically. Comparisons are made with the results predicted by different theories Lord-Shulman theory (L-S), the Green-Naghdi theory of type III (G-N III) and the three-phase-lag model in the absence and presence of a magnetic field, rotation, initial stress and gravity. The results indicate that the effect of rotation, magnetic field, initial stress and gravity field are very pronounced.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14

Similar content being viewed by others

References

  • Abd-Alla AM, Othman MIA, Abo-Dahab SM (2016a) Reflection of plane waves from electro-magneto-thermoelastic half-space with a dual-phase. CMC-Comp Mater Cont 51:63–79

    Google Scholar 

  • Abd-Alla AM, Abo-Dahab SM, Kilany AA (2016b) SV-waves incidence at interface between solid–liquid media under electromagnetic field and initial stress in the context of the thermoelastic theories. J Therm Stress 39:960–976

    Article  Google Scholar 

  • Abd-Alla AM, Abo-Dahab SM, Alotabi Hind A (2017a) On the influence of thermal stress and magnetic field in thermoelastic half-space without energy dissipation. J Therm Stress 40:213–230

    Article  Google Scholar 

  • Abd-Alla AM, Abo-Dahab SM, Khan Aftab (2017b) Rotational effect of thermoelastic Stoneley, Love and Rayleigh waves in fibre-reinforced anisotropic general viscoelastic media of higher order. Struct Eng Mech 61:221–230

    Article  Google Scholar 

  • Abd-Alla AM, Abo-Dahab SM, Alotabi Hind A (2017c) Propagation of a thermoelastic wave in a half-space of a homogeneous isotropic material subjected to the effect of gravity field. Arch Civil Mech Eng 17:564–573

    Article  Google Scholar 

  • Abo-Dahab SM, Abd-Alla AM (2016) Green Lindsay model on reflection and refraction of p- and SV-waves at interface between solid–liquid media presence in magnetic field and initial stress. J Vib Cont 22(12):3426–3438

    Article  MathSciNet  MATH  Google Scholar 

  • Abo-Dahab SM, Biswas S (2017) Effect of rotation on Rayleigh waves in magneto-thermoelastic transversely isotropic medium with thermal relaxation times. J Electromagn Waves Appl 31(15):1485–1507

    Article  Google Scholar 

  • Abo-Dahab SM, Abd-Alla AM, Alqarni AJ (2017) A two-dimensional problem with rotation and magnetic field in the context of four thermoelastic theories. Results Phys 7:2742–2751

    Article  Google Scholar 

  • Ailawalia P, Narah NS (2009) Effect of rotation in generalized thermoelastic solid under the influence of gravity with an overlying infinite thermoelastic fluid. Appl Math Mech 30:1505–1518

    Article  MathSciNet  MATH  Google Scholar 

  • Chakraborty N, Singh MC (2011a) Reflection and refraction of a plane thermoelastic wave at a solid–solid interface under perfect boundary condition, in presence of normal initial stress. Appl Math Model 35(11):5286–5301

    Article  MathSciNet  MATH  Google Scholar 

  • Chakraborty N, Singh MC (2011b) Reflection and refraction of a plane thermoelastic plane wave at a solid–solid Interface under perfect boundary condition, in presence of normal initial stress. Appl Math Model 35:5286–5301

    Article  MathSciNet  MATH  Google Scholar 

  • Elsagheer M, Abo-Dahab SM (2016) Reflection of thermoelastic waves from insulated boundary fibre-reinforced half-space under influence of rotation and magnetic field. Appl Math Inf Sci 10(3):1129–1140

    Article  Google Scholar 

  • Kumar R, Kaur M (2014) Reflection and refraction of plane waves at the interface of an elastic solid and microstretch thermoelastic solid with microtemperatures. Arch Appl Mech 84(4):571–590

    Article  MATH  Google Scholar 

  • Lykotrafitis G, Georgiadis HG, Brock LM (2001) Three-dimensional thermoelastic wave motions in a half-space under the action of a buried source. Int J Solid Struct 38:4857–4878

    Article  MATH  Google Scholar 

  • Othman MIA, Song YQ (2008) Reflection of magneto-thermoelastic waves with two relaxation times and temperature dependent elastic moduli. Appl Math Model 32(4):483–500

    Article  MathSciNet  MATH  Google Scholar 

  • Othman MIA, Lotfy Kh, Farouk RM (2010) Generalized thermomicrostretch elastic medium with temperature dependent properties for different theories. Eng Anal Bound Elem 34(3):229–237

    Article  MathSciNet  MATH  Google Scholar 

  • Said SM (2015) Deformation of a rotating two-temperature generalized magneto-thermo-elastic medium with internal heat source due to hydrostatic initial stress. Meccanica 50:115–123

    Article  Google Scholar 

  • Said SM (2016a) Two-temperature generalized magneto-thermoelastic medium for dual-phase-lag model under the effect of gravity field and hydrostatic initial stress. Multidiscip Model Mater Struct 12(2):362–383

    Article  Google Scholar 

  • Said SM (2016b) Influence of gravity on generalized magneto-thermoelastic medium for three-phase-lag model. J Comput Appl Math 291:50–68

    Article  MathSciNet  Google Scholar 

  • Singh B (2008) Effect of hydrostatic initial stresses on waves in a thermoelastic solid half-space. Appl Math Comput 198(2):494–505

    MathSciNet  MATH  Google Scholar 

  • Xiong C, Guo Y (2016) Effect of variable properties and moving heat source on magnetothermoelastic problem under fractional order thermoelasticity. Adv Mater Sci Eng 2016:12

    Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Mathematics, Faculty of Science, South Valley University, Qena, 83523, Egypt

    S. M. Abo-Dahab

  2. Department of Mathematics, Faculty of Science, Taif University, Taif, Saudi Arabia

    S. M. Abo-Dahab

  3. Department of Mathematics, Faculty of Science, Sohag University, Sohag, 82524, Egypt

    A. M. Abd-Alla, A. A. Kilany & M. Elsagheer

Authors
  1. S. M. Abo-Dahab
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. A. M. Abd-Alla
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. A. A. Kilany
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. M. Elsagheer
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to A. M. Abd-Alla.

Appendix

Appendix

We represent \(A,\,B,\,C,\,D\) and \(E\) in terms \(L = C_{k} - \iota C_{\nu } \omega - C_{T} \omega^{2} ,\quad M = \zeta_{0} + \zeta_{1} \omega^{2} ,\) \(N = \zeta_{8} + \zeta_{9} \omega^{2} ,\quad R = - \frac{{C_{2}^{2} }}{{\omega^{*2} }} + \omega^{2} ,\quad S = \frac{{2kc_{0}^{2} }}{{\gamma \omega^{*2} }} - \frac{{j\rho c_{0}^{2} \omega^{2} }}{\gamma }\) as follow:

$$A = \frac{{C_{1}^{2} }}{{c_{0}^{2} }}L,$$
$$\begin{aligned} B & = - LR - \zeta_{5} \frac{{C_{3}^{2} }}{{\omega^{*2} }}L - \frac{{\zeta_{10} kC_{1}^{2} }}{{\gamma \omega^{*2} }}L + \frac{{C_{1}^{2} }}{{c_{0}^{2} }}(LS - \omega^{2} \tau_{q}^{*} - \zeta_{4} \varepsilon_{1} \omega^{2} \tau_{q}^{*} - LM - LN - \zeta_{2} \zeta_{6} \sin^{2} \theta L), \\ C & = \omega^{2} \tau_{q}^{*} R - a_{0} \varepsilon_{2} \omega^{2} \tau_{q}^{*} + \varepsilon_{2} \omega^{2} \tau_{q}^{*} \zeta_{4} \frac{{C_{3}^{2} }}{{\omega^{*2} }} + \, \varepsilon_{1} \omega^{2} \tau_{q}^{*} \zeta_{4} R + a_{0} \varepsilon_{1} \omega^{2} \tau_{q}^{*} \zeta_{5} + LMR + \omega^{2} \tau_{q}^{*} \frac{{C_{1}^{2} }}{{c_{0}^{2} }}M + LNR \\ & \quad + \omega^{2} \tau_{q}^{*} \frac{{C_{1}^{2} }}{{c_{0}^{2} }}N - LRS - \omega^{2} \tau_{q}^{*} \frac{{C_{1}^{2} }}{{c_{0}^{2} }}S + \omega^{2} \tau_{q}^{*} \zeta_{5} \frac{{C_{3}^{2} }}{{\omega^{*2} }} + \zeta_{2} \zeta_{6} \sin^{2} \theta LR + \zeta_{2} \zeta_{6} \omega^{2} \tau_{q}^{*} \sin^{2} \theta \frac{{C_{1}^{2} }}{{c_{0}^{2} }} \\ & \quad + \zeta_{5} \frac{{C_{3}^{2} }}{{\omega^{*2} }}LN + \varepsilon_{1} \omega^{2} \tau_{q}^{*} \zeta_{4} \frac{{C_{1}^{2} }}{{c_{0}^{2} }}N - \zeta_{5} \frac{{C_{3}^{2} }}{{\omega^{*2} }}LS - \varepsilon_{1} \omega^{2} \tau_{q}^{*} \zeta_{4} \frac{{C_{1}^{2} }}{{c_{0}^{2} }}S + \zeta_{10} \frac{{kc_{0}^{2} }}{{\gamma \omega^{*2} }}LR + \zeta_{10} \omega^{2} \tau_{q}^{*} \frac{{kC_{1}^{2} }}{{\gamma \omega^{*2} }} \\ & \quad - \zeta_{3} \zeta_{7} \omega^{2} \frac{{C_{1}^{2} }}{{c_{0}^{2} }}L + \frac{{C_{1}^{2} }}{{c_{0}^{2} }}LMN - \frac{{C_{1}^{2} }}{{c_{0}^{2} }}LMS - \frac{{C_{1}^{2} }}{{c_{0}^{2} }}LNS + \zeta_{5} \zeta_{10} \frac{{C_{3}^{2} kc_{0}^{2} }}{{\gamma \omega^{*4} }}L + \varepsilon_{1} \omega^{2} \tau_{q}^{*} \zeta_{4} \zeta_{10} \frac{{kC_{1}^{2} }}{{\gamma \omega^{*2} }} \\ & \quad - \zeta_{2} \zeta_{6} \sin^{2} \theta \frac{{C_{1}^{2} }}{{c_{0}^{2} }}LS + \zeta_{10} \frac{{kC_{1}^{2} }}{{\gamma \omega^{*2} }}LM, \\ \end{aligned}$$
$$\begin{aligned} D & = a_{0} \varepsilon_{2} \omega^{2} \tau_{q}^{*} M + a_{0} \varepsilon_{2} \omega^{2} \tau_{q}^{*} N - a_{0} \varepsilon_{2} \omega^{2} \tau_{q}^{*} S - \omega^{2} \tau_{q}^{*} MR - \omega^{2} \tau_{q}^{*} NR + \omega^{2} \tau_{q}^{*} RS - \varepsilon_{2} \omega^{2} \tau_{q}^{*} \zeta_{4} \frac{{C_{3}^{2} }}{{\omega^{*2} }}N \\ & \quad + \varepsilon_{2} \omega^{2} \tau_{q}^{*} \zeta_{4} \frac{{C_{3}^{2} }}{{\omega^{*2} }}S + a_{0} \varepsilon_{2} \omega^{2} \tau_{q}^{*} \zeta_{2} \zeta_{6} \sin^{2} \theta + a_{0} \varepsilon_{2} \omega^{2} \tau_{q}^{*} \zeta_{10} \frac{{kc_{0}^{2} }}{{\gamma \omega^{*2} }} + \zeta_{3} \zeta_{7} \omega^{2} LR + \zeta_{3} \zeta_{7} \omega^{4} \tau_{q}^{*} \frac{{C_{1}^{2} }}{{c_{0}^{2} }} \\ & \quad - \zeta_{2} \zeta_{6} \omega^{2} \tau_{q}^{*} \sin^{2} \theta R\, - \omega^{2} \tau_{q}^{*} \zeta_{5} \frac{{C_{3}^{2} }}{{\omega^{*2} }}N - \varepsilon_{1} \omega^{2} \tau_{q}^{*} \zeta_{4} NR + \omega^{2} \tau_{q}^{*} \zeta_{5} \frac{{C_{3}^{2} }}{{\omega^{*2} }}S + \varepsilon_{1} \omega^{2} \tau_{q}^{*} \zeta_{4} RS \\ & \quad - \omega^{2} \tau_{q}^{*} \zeta_{10} \frac{{kc_{0}^{2} }}{{\gamma \omega^{*2} }}R - a_{0} \varepsilon_{1} \omega^{2} \tau_{q}^{*} \zeta_{5} N + a_{0} \varepsilon_{1} \omega^{2} \tau_{q}^{*} \zeta_{5} S - LMNR - \omega^{2} \tau_{q}^{*} \frac{{C_{1}^{2} }}{{c_{0}^{2} }}MN + LMRS \\ & \quad + \omega^{2} \tau_{q}^{*} \frac{{C_{1}^{2} }}{{c_{0}^{2} }}MS + LNRS + \omega^{2} \tau_{q}^{*} \frac{{C_{1}^{2} }}{{c_{0}^{2} }}NS - \omega^{2} \tau_{q}^{*} \zeta_{5} \zeta_{10} \frac{{C_{3}^{2} }}{{\omega^{*2} }}\frac{{kc_{0}^{2} }}{{\gamma \omega^{*2} }} + \omega^{2} \tau_{q}^{*} \zeta_{2} \zeta_{6} \sin^{2} \theta \frac{{C_{1}^{2} }}{{c_{0}^{2} }}S \\ & \quad - \varepsilon_{1} \omega^{2} \tau_{q}^{*} \zeta_{4} \zeta_{10} \frac{{kc_{0}^{2} }}{{\gamma \omega^{*2} }}R - a_{0} \varepsilon_{1} \omega^{2} \tau_{q}^{*} \zeta_{5} \zeta_{10} \frac{{kc_{0}^{2} }}{{\gamma \omega^{*2} }} + \zeta_{2} \zeta_{6} \sin^{2} \theta LRS\, - \zeta_{3} \zeta_{7} \omega^{2} \frac{{C_{1}^{2} }}{{c_{0}^{2} }}LS \\ & \quad + \zeta_{5} \frac{{C_{3}^{2} }}{{\omega^{*2} }}LNS + \varepsilon_{1} \omega^{2} \tau_{q}^{*} \zeta_{4} \frac{{C_{1}^{2} }}{{c_{0}^{2} }}NS - \zeta_{10} \frac{{kc_{0}^{2} }}{{\gamma \omega^{*2} }}LMR - \zeta_{10} \frac{{kC_{1}^{2} }}{{\gamma \omega^{*2} }}M + \frac{{C_{1}^{2} }}{{c_{0}^{2} }}LMNS \\ & \quad - \varepsilon_{2} \omega^{2} \tau_{q}^{*} \zeta_{4} \zeta_{10} \frac{{C_{3}^{2} kc_{0}^{2} }}{{\gamma \omega^{*4} }}, \\ \end{aligned}$$
$$\begin{aligned} E & = a_{0} \varepsilon_{2} \omega^{4} \tau_{q}^{*} \zeta_{3} \zeta_{7} - a_{0} \varepsilon_{2} \omega^{2} \tau_{q}^{*} MN + a_{0} \varepsilon_{2} \omega^{2} \tau_{q}^{*} MS + a_{0} \varepsilon_{2} \omega^{2} \tau_{q}^{*} NS + \omega^{4} \tau_{q}^{*} \zeta_{3} \zeta_{7} R + \omega^{2} \tau_{q}^{*} MNR \\ & \quad - \omega^{2} \tau_{q}^{*} MRS + \zeta_{3} \zeta_{7} \omega^{2} LRS + \omega^{4} \tau_{q}^{*} \zeta_{3} \zeta_{7} \frac{{C_{1}^{2} }}{{c_{0}^{2} }}S - \omega^{2} \tau_{q}^{*} \zeta_{2} \zeta_{6} \sin^{2} \theta RS - a_{0} \varepsilon_{2} \omega^{2} \tau_{q}^{*} \zeta_{10} \frac{{kc_{0}^{2} }}{{\gamma \omega^{*2} }}M\, \\ & \quad - \omega^{2} \tau_{q}^{*} \zeta_{5} \frac{{C_{3}^{2} }}{{\omega^{*2} }}NS - \varepsilon_{1} \omega^{2} \tau_{q}^{*} \zeta_{4} NRS + \omega^{2} \tau_{q}^{*} \zeta_{10} \frac{{kc_{0}^{2} }}{{\gamma \omega^{*2} }}MR - a_{0} \varepsilon_{1} \omega^{2} \tau_{q}^{*} \zeta_{5} NS - LMNRS \\ & \quad - \omega^{2} \tau_{q}^{*} \frac{{C_{1}^{2} }}{{c_{0}^{2} }}MNS - \varepsilon_{2} \omega^{2} \tau_{q}^{*} \zeta_{4} \frac{{C_{3}^{2} }}{{\omega^{*2} }}NS + a_{0} \varepsilon_{2} \omega^{2} \tau_{q}^{*} \zeta_{2} \zeta_{6} \sin^{2} \theta S - \omega^{2} \tau_{q}^{*} NRS, \\ \end{aligned}$$
$$F = a_{0} \varepsilon_{2} \omega^{4} \tau_{q}^{*} \zeta_{3} \zeta_{7} S - a_{0} \varepsilon_{2} \omega^{2} \tau_{q}^{*} MNS - \omega^{2} \tau_{q}^{*} \zeta_{3} \zeta_{7} \omega^{2} RS + \omega^{2} \tau_{q}^{*} MNRS.$$

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Abo-Dahab, S.M., Abd-Alla, A.M., Kilany, A.A. et al. Effect of rotation and gravity on the reflection of P-waves from thermo-magneto-microstretch medium in the context of three phase lag model with initial stress. Microsyst Technol 24, 3357–3369 (2018). https://doi.org/10.1007/s00542-017-3697-x

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00542-017-3697-x

Search

Navigation