Effect of gas rarefaction on the quality factors of micro-beam resonators

Abstract

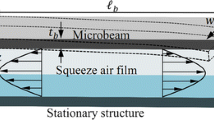
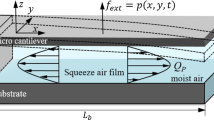
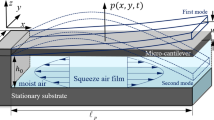
The external squeeze film damping (SFD) of microelectromechanical systems (MEMS) resonators is a dominant factor to lower the quality factor (Q-factor) due to their large surface area to volume ratio and small spacing. To improve the Q-factor of MEMS resonators, the effect of gas rarefaction (low gas ambient pressure in thin gas film thickness) or operating in higher mode should be considered in SFD analysis. The modified molecular gas lubrication (MMGL) equation is applied for modeling the SFD with gas rarefaction effects taken into consideration. The effects of inverse Knudsen number, surface accommodation coefficients (ACs) and operating frequency on SFD are discussed. The combined effects of SFD, thermoelastic damping (TED) and anchor loss on the total Q-factors of MEMS resonators are considered. The contribution of SFD on the total Q-factor (weighting of SFD) is also discussed. The results show that weighting of SFD could be decrease at low inverse Knudsen number or low ACs or operating at high resonant frequencies.

Appendices

Appendix 1

In the case of flexural vibration of homogeneous rectangular beams, Zener (1937, 1938) have developed a simple approximate expression to estimate $Q_{TED}$ with various vibrational frequencies ($\omega_{n}$) of the thin beams as following

$$\frac{1}{Q} = \left( {\frac{{E\alpha_{S}^{2} T_{0} }}{{\rho_{m} C_{p} }}} \right)\left( {\frac{{\omega_{n} \tau_{R} }}{{1 + (\omega_{n} \tau_{R} )^{2} }}} \right)$$

(12)

The thermal relaxation times ($\tau_{R}$) associated with the transverse thermal modes of the thin beams given by

$$\tau_{R} = \frac{{\rho_{m} C_{p} t_{b}^{2} }}{{\pi^{2} \kappa }}$$

(13)

In the Zener’s the standard theory of TED, the internal friction of the vibrational structures, is analytically given by Eqs. (12) and (13) as functions of the properties of material, thermal relaxation time and vibrational frequency of the thin beams. When $\omega_{n} \ll \tau_{R}^{ - 1}$, the vibration is isothermal, the vibrational system is remained in thermal equilibrium. When $\omega_{n} \gg \tau_{R}^{ - 1}$, the vibration is adiabatic, the vibrational system has no time to relax. Thus, there is a little energy dissipated for each case. On the other hand, when the vibrational frequency is very close to the effective thermal relaxation time ($\omega_{n} \cong \tau_{R}^{ - 1}$) or ($\omega_{n} \tau_{R} \cong 1$), maximum of internal friction of the beam occurs at position of dissipation peak or so-called Debye peak.

Appendix 2

TED, which is one of dominant damping sources in micro-beam resonators, is very sensitive with the mode of resonator. The operating properties of material are used in this comparison with thermal conductivity $\kappa$ = 90 [W/(m K)], specific heat capacity $C_{P}$ = 700 [J/(kg K)], thermal expansion coefficient $\alpha_{S} = 2.6 \times 10^{ - 6}$ (1/K), initial beam temperature $T_{0}$ = 300 (K). As listed in Table 2, the magnitude of $Q_{TED}$ varies significantly with the modes of the micro-beam resonator. TED increases and reaches to a maximum value at the 7th mode, and then the $Q_{TED}$ decreases as the mode of micro-beam resonator increase. That’s because of the internal friction of flexural micro-beam resonator becomes more pronounced when the vibrational frequency is nearly closed to the structural relaxation time ($\omega_{n} \cong \tau_{R}^{ - 1}$). Also, the calculated results of $Q_{TED}$ were compared against with the analytical results that calculate from the model of Zener (1937, 1938) (see Appendix 1) for various flexural modes of micro-beam resonator with the some errors. The errors may come from the simple assumption of Zener’s equation with the structure is very thin and there is no stress perpendicular to the plane. While looking at the 3D model in detail, we found that stresses and their spatial derivations have components of equal magnitude in all three directions. Thus, the results of $Q_{TED}$ are numerically computed by the 3D model are approximately agreed to that of Zener’s calculation.

Anchor loss is another important damping in MEMS resonators, can also become dominant in higher modes of the resonators. In Table 3, the results of Q-factor of anchor loss ($Q_{anch}$) are calculated from the model’s Hao et al. (2003) for various flexural modes of the micro-beam resonator. The values of $C_{F(n)}$, which is related to various resonant modes, can be obtained from the results of Hao’s paper for various modes of micro-beam resonators. The valid conditions of ${{\lambda_{T} } \mathord{\left/ {\vphantom {{\lambda_{T} } {w_{b} }}} \right. \kern-0pt} {w_{b} }} \gg 1$ in Eq. (9) can be satisfied for various resonant mode conditions. The $Q_{anch}$ decreases significantly (anchor loss increases) as the mode of resonator increases (higher vibrational frequency).

Appendix 3

In Sect. 2, we proposed the governing equations of the transverse vibration equation (Eq. 2), the MMGL equation (Eq. 5) and the thermal equation (Eq. 8) for the TED and the SFD problem on the Q-factors of the micro-beam resonators. For further derivations, we linearize these equations (Eqs. 2, 5, 8) by assuming small variations for transverse displacement of the beam, gas film pressure and temperature of the beam ($p_{a}$, $h_{0}$ and $T_{0}$ are constants) as

$$h(x,y,t) = h_{0} - w(x,y,t)$$

(14)

$$p(x,y,t) = p_{a} + \bar{p}(x,y,t)$$

(15)

$$T(x,y,t) = T_{0} + \bar{T}(x,y,t)$$

(16)

The Poiseuille flow rate may thus be expressed as

$$Q_{P} (D) = Q_{P} (D_{0} ) + \left( {\frac{{\partial Q_{P} }}{\partial p}} \right) \cdot \bar{p} - \left( {\frac{{\partial Q_{P} }}{\partial h}} \right) \cdot w$$

(17)

The equation for the transverse displacement of the micro-beam (Leissa 1969), Eq. (2), is

$$D_{b} \left( {\frac{{\partial^{4} w}}{{\partial x^{4} }} + 2\frac{{\partial^{4} w}}{{\partial x^{2} \partial y^{2} }} + \frac{{\partial^{4} w}}{{\partial y^{4} }}} \right) + \rho_{m} t_{b} \frac{{\partial^{2} w}}{{\partial t^{2} }} = - \bar{p}(x,y,t)$$

(18)

with boundary conditions at the fixed edges $x = 0$

$$w(x,y,t) = 0$$

(19)

$$\frac{\partial w(x,y,t)}{\partial x} = 0$$

(20)

and at the free edges:

$$\frac{{\partial^{2} w(x,y,t)}}{{\partial x^{2} }} = \frac{{\partial^{3} w(x,y,t)}}{{\partial x^{3} }} = 0\;{\text{at}}\;x = \ell_{b}$$

(21)

$$\frac{{\partial^{2} w(x,y,t)}}{{\partial y^{2} }} = \frac{{\partial^{3} w(x,y,t)}}{{\partial y^{3} }} = 0\;{\text{at}}\;y = 0\;{\text{and}}\;y = w_{b}$$

(22)

Substituting Eqs. (14), (15) and (17) into Eq. (5), we can obtain the linearized MMGL equation as

$$\frac{\partial }{\partial x}\left( {\frac{{p_{a} h_{0}^{3} }}{{12\mu_{0} }}\frac{{\partial \bar{p}}}{\partial x}Q_{P} (D_{0} )} \right) + \frac{\partial }{\partial y}\left( {\frac{{p_{a} h_{0}^{3} }}{{12\mu_{0} }}\frac{{\partial \bar{p}}}{\partial y}Q_{P} (D_{0} )} \right)\; = \left( {h_{0} \frac{{\partial \bar{p}}}{\partial t} - p_{a} \frac{\partial w}{\partial t}} \right)$$

(23)

The linearized pressure boundary conditions are

$$\bar{p}(x,0,t) = \bar{p}(x,w_{b} ,t) = \bar{p}(\ell_{b} ,y,t) = 0$$

(24)

$$\frac{{\partial \bar{p}(0,y,t)}}{\partial x} = 0$$

(25)

The linearized thermal equation for the micro-beam resonators can be obtained as

$$\nabla \cdot (\kappa \nabla \bar{T}) = \rho_{m} C_{p} \frac{{\partial \bar{T}}}{\partial t} + \frac{{E\alpha_{S} T_{0} }}{1 - 2v} \cdot \frac{{\partial (\varepsilon_{x} + \varepsilon_{y} + \varepsilon_{z} )}}{\partial t}$$

(26)

Thermal gradients are set zero for all the boundaries of the beam

$$\frac{{\partial \bar{T}}}{\partial x} = 0\;{\text{at}}\;x = 0\;{\text{and}}\;x = \ell_{b}$$

(27)

$$\frac{{\partial \bar{T}}}{\partial y} = 0\;{\text{at}}\;y = 0\;{\text{and}}\;y = w_{b}$$

(28)

$$\frac{{\partial \bar{T}}}{\partial z} = 0\;{\text{at}}\;z = 0\;{\text{and}}\;z = t_{b}$$

(29)

The harmonic variations of the transverse displacement of the beam, gas film pressure and beam temperature are given by

$$w(x,y,t) = \tilde{w}(x,y)e^{\lambda t}$$

(30)

$$\bar{p}(x,y,t) = \tilde{p}(x,y)e^{\lambda t}$$

(31)

$$\bar{T}(x,y,t) = \tilde{T}(x,y)e^{\lambda t}$$

(32)

By substituting Eqs. (30) and (31) into Eq. (18), we can obtain

$$D_{b} \left( {\frac{{\partial^{4} \tilde{w}}}{{\partial x^{4} }} + 2\frac{{\partial^{4} \tilde{w}}}{{\partial x^{2} \partial y^{2} }} + \frac{{\partial^{4} \tilde{w}}}{{\partial y^{4} }}} \right) + \tilde{p} = - \lambda^{2} \rho_{m} t_{b} \tilde{w}$$

(33)

with corresponding boundary conditions

$$\tilde{w}(x,y) = 0,\;\frac{{\partial \tilde{w}(x,y)}}{\partial x} = 0\;{\text{at}}\;x = 0$$

(34)

$$\frac{{\partial^{2} \tilde{w}(x,y)}}{{\partial x^{2} }} = \frac{{\partial^{3} \tilde{w}(x,y)}}{{\partial x^{3} }} = 0\;{\text{at}}\;x = \ell_{b}$$

(35)

$$\frac{{\partial^{2} \tilde{w}(x,y)}}{{\partial y^{2} }} = \frac{{\partial^{3} \tilde{w}(x,y)}}{{\partial y^{3} }} = 0\;{\text{at}}\;y = 0\;{\text{and}}\;y = w_{b}$$

(36)

Then we substitute Eqs. (30) and (31) into Eq. (23), we can obtain

$$\frac{\partial }{\partial x}\left( {\frac{{p_{a} h_{0}^{3} }}{{12\mu_{0} }}\frac{{\partial (\tilde{p})}}{\partial x}Q_{P} (D_{0} )} \right) + \frac{\partial }{\partial y}\left( {\frac{{p_{a} h_{0}^{3} }}{{12\mu_{0} }}\frac{{\partial (\tilde{p})}}{\partial y}Q_{P} (D_{0} )} \right)\; = \lambda \left( {h_{0} \tilde{p} - p_{a} \tilde{w}} \right)$$

(37)

with corresponding boundary conditions

$$\tilde{p}(x,0) = \tilde{p}(x,w_{b} ) = \tilde{p}(\ell_{b} ,y) = 0$$

(38)

$$\frac{{\partial \tilde{p}(0,y)}}{\partial x} = 0$$

(39)

Next, we substitute Eqs. (30) and (32) into Eq. (26), we can obtain

$$\nabla (\kappa \cdot \nabla \tilde{T}) = \lambda \left( {\rho_{m} C_{p} \tilde{T} + \frac{{E\alpha_{S} T_{0} }}{1 - 2v}\tilde{w}} \right)$$

(40)

with corresponding boundary conditions for themal problem

$$\frac{{\partial \tilde{T}}}{\partial x} = 0\;at\;x = 0\;\text{and}\;x = \ell_{b}$$

(41)

$$\frac{{\partial \tilde{T}}}{\partial y} = 0\;at\;y = 0\;{\text{and}}\;y = w_{b}$$

(42)

$$\frac{{\partial \tilde{T}}}{\partial z} = 0\;at\;z = 0\;{\text{and}}\;z = t_{b}$$

(43)

From the eigenvalue problems of Eqs. (33–39), we can solve the eigenvalue ($\lambda$) for the SFD of the micro-beam resonators by the finite element methods (FEM) (Reddy 1993), thus $Q_{SFD} = \left| {\frac{{\text{Im} (\lambda )}}{{2\text{Re} (\lambda )}}} \right|$. From the eigenvalue problems of Eqs. (33–36) and Eqs. (40-43), we can solve the eigenvalue ($\lambda$) for the TED of the micro-beam resonators by the FEM, thus $Q_{TED} = \left| {\frac{{\text{Im} (\lambda )}}{{2\text{Re} (\lambda )}}} \right|$.