On uniqueness of vector-valued minimizers of the Ginzburg-Landau functional in annular domains

Abstract.

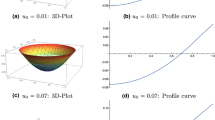
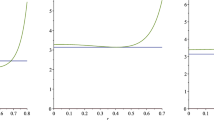
Consider a class of Sobolev functions satisfying a prescribed degree condition on the boundary of a planar annular domain. It is shown that, within this class, the Ginzburg-Landau functional possesses the unique, radially symmetric minimizer, provided that the annulus is sufficiently narrow. This result is known to be false for wide annuli where vortices are energetically feasible. The estimate for the critical radius below which the uniqueness of the minimizer is guaranteed is obtained as well.