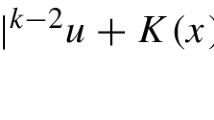Multiplicity results for (p, q)-Laplacian equations with critical exponent in ${\mathbb {R}}^N$ and negative energy

Abstract

We prove existence results in all of ${\mathbb {R}}^N$ for an elliptic problem of (p, q)-Laplacian type involving a critical term, nonnegative weights and a positive parameter $\lambda$. In particular, under suitable conditions on the exponents of the nonlinearity, we prove existence of infinitely many weak solutions with negative energy when $\lambda$ belongs to a certain interval. Our proofs use variational methods and the concentration compactness principle. Towards this aim we give a detailed proof of tight convergence of a suitable sequence.

1 Introduction

In this paper we are interested in nontrivial weak solutions in $D^{1,p}({\mathbb {R}}^N)\cap D^{1,q}({\mathbb {R}}^N)$ of the following nonlinear elliptic problem of (p, q)-Laplacian type involving a critical term

where $\Delta _{m}u=\text{ div }(|Du|^{m-2}D u)$ is the m-Laplacian of u, $1<q<p<N$, $p^{*}=\frac{Np}{N-p}$ is the critical Sobolev’s exponent, the parameter $\lambda$ is positive, the exponent k is such that $1<k<p^*$ and the weights are nontrivial and satisfy

$$\begin{aligned} 0\le V\in L^{r}({\mathbb {R}}^{N}), \quad r=\frac{p^{*}}{p^{*}-k}, \end{aligned}$$

(1)

and

$$\begin{aligned} 0\le K\in C({\mathbb R}^N) \cap L^\infty ({\mathbb R}^N) \end{aligned}$$

(2)

In particular, by using variational methods and concentration compactness principles, we prove multiplicity results for solutions of $({\mathcal {P}})$ with negative energy when

$$\begin{aligned} 1<q<k<p<N. \end{aligned}$$

(3)

Towards this aim, we have to deal with a particular property for a sequence of measures called “tightness”, following a probabilistic terminology, required in the second concentration compactness principle by Lions [27,28,29,30]. We faced this delicate point in Lemma 7 below for all k with $1<k<p^*$.

We recall that a first serious problem on unbounded domains is the loss of compactness of the Sobolev’s embeddings, which renders variational techniques more delicate.

In addition, critical problems in ${\mathbb {R}}^N$ represent one of the most dramatic cases of loss of compactness and have been studied intensively in the last 25 years, starting with the pioneering paper by Brezis and Nirenberg [6] for the Laplacian. Later, the p-Laplacian case in the entire ${\mathbb {R}}^N$ was investigated by many authors, we refer to [2, 12, 13, 16, 23, 42] in exterior domains, [17] with double critical nonlinearities, [15, 20] and the references therein. Among these papers, we mention that by Swanson and Yu [42], in which they consider morally the subcase of $({\mathcal {P}})$ with $p<k<p^*$ and $\lambda =1$, that is with no parameter.

The single p-Laplacian case of $({\mathcal {P}})$ in a bounded domain without weights is completely described for all parameter $\lambda >0$ by Garcia Azorero and Peral in [3], where they obtain, among other results, two positive values $\lambda _0, \, \lambda _1$ such that existence of a nontrivial solution holds for $\lambda \ge \lambda _0$ if $1<p<k<p^*$, while existence of infinitely many solution holds if $1<k<p$ for $\lambda \in (0,\lambda _1)$.

Critical Dirichlet problems for (p, q)-Laplacian on bounded domains are studied in [26] where the authors extend partially the multiplicity result due to [3], again without weights, for $1<k<p$, then in [21] where it is proved that the analogous result given in [26] holds when weights are included if k satisfies further restrictions beyond $p<k<p^*$. Furthermore, in [43] the case $1<q<p<k<p^*$ is treated obtaining the existence of a nontrivial solution for $\lambda \ge \lambda _0>0$ (see also [14] for $p>q\ge 2$).

Among papers on bounded domains, we mention that by Cherfils and Il’yasov [10], in which, in the subcritical case, nonexistence of solutions for $\lambda$ small and existence for $\lambda$ large can be deduced by using a suitable nonlinear spectral analysis. In this direction, we quote the papers by Papageorgiu et al. [36, 38]; in particular, in the first they study existence of ground state solutions for a differential operator given by the sum of a p-Laplacian and of a weighted q-Laplace operator with a positive $L^\infty$ weight not bounded away from zero, while in [36] they give existence of a continuous spectrum for the Dirichlet problem with a differential operator given by a linear combination of p and q-Laplacian, so that existence of solutions occurs. For a detailed theory on the subject we refer to the book [37].

Moving to the unbounded case, the situation is fairly delicate. Furthermore, condition $({\mathcal {P}})$ is new, since only the cases $1<k<q<p$ or $1<q<p<k<p^*$ are partially investigated in literature, respectively in [9, 22] and in [31], as far as we know.

The (p, q)-Laplacian problem $({\mathcal {P}})$ comes from a general reaction-diffusion system

$$\begin{aligned} u_{t}-\Delta _{p}u-\Delta _{q}u=c(x,u). \end{aligned}$$

(4)

The system has wide range of applications in physics and related sciences, such as biophysics, chemical reaction and plasma physics. In such applications, the function u describes a concentration, the p and q Laplacian terms in (4) correspond to the diffusion where the diffusion coefficient is $|D u|^{p-2}+|D u|^{q-2}$, whereas the term c(x, u) is the reaction and relates to sources and loss processes. Typically, in chemical and biological applications, the reaction term c(x, u) has a polynomial form with respect to the concentration u.

The case $q=2$, that is (p, 2)-Laplacian, recently was studied by Papageorgiou et al. in [33, 34] and [35], where they prove existence and multiplicity theorems by using a variational approach and Morse theory with $p>2$. In particular, in [33], they consider parametric equations when the parameter $\lambda$ is near to the principal eigenvalue $\lambda _{1}(p)>0$ of $(-\Delta _{p},W_{0}^{1,p}(\Omega ))$, while in [34] and [35], they consider equations where the reaction term satisfies particular conditions which imply the resonance of problem at $\pm \infty$ and at $0^{\pm }$.

Another important example, widely studied, in which a subcase of problem $({\mathcal {P}})$ appears, is the study of solitary waves or solitons which are special solutions whose profile remains unchanged under the evolution in time, of the nonlinear Schrödinger equation see [7, 10, 41], of the typical form

$$\begin{aligned} i \frac{\partial \psi }{\partial t}+\Delta \psi +\Delta _q \psi -U(x)\psi +|\psi |^{k-1}\psi =0, \quad 2<k<2^*, \end{aligned}$$

(5)

where i is the imaginary unit and the function U is the potential. In particular, a function $\psi (x,t)=e^{-i\omega t}u(x)$ is a standing-wave solution of (5), where $\omega \in {\mathbb {R}}$ is the energy, if and only if the function u satisfies

$$\begin{aligned} -\Delta u-\Delta _q u+[U(x)-\omega ]u=|u|^{k-1}u. \end{aligned}$$

The subcase of (5) when $q=2$ and a cubic nonlinearity, $k=3$, is involved is called the Gross–Pitaevskii equation.

A strategy to prove multiplicity of solutions of $({\mathcal {P}})$, is to apply the result of multiple critical points for the energy functional $E_\lambda$ associated to $({\mathcal {P}})$, given by

$$\begin{aligned} E_{\lambda }(u)=\frac{1}{p}\Vert D u\Vert _p^{p}+\frac{1}{q}\Vert D u\Vert _q^{q} -\frac{\lambda }{k}\int _{{\mathbb {R}}^N}V|u|^{k}dx-\frac{1}{p^{*}}\int _{{\mathbb {R}}^N}K|u|^{p^{*}}dx. \end{aligned}$$

(6)

In particular, we make use of the classical multiplicity result by Rabinowitz in [39] for even functionals, so that 0 is a critical point and critical points occur in antipodal pairs. Under further conditions, the functional possesses additional critical points. Precisely, we apply Theorem 1.9 in [39] in which the Krasnoselskii genus is involved with its properties and furthermore the standard and crucial compactness condition (PS)$_c$ is required to be satisfied by $E_\lambda$, for $c<0$. This is a delicate point, indeed for critical problems in all of ${\mathbb {R}}^N$ this compactness condition is often loss, for this reason some of the papers treating problems on unbounded domains use special function spaces where the compactness is preserved, such as spaces of radially symmetric functions or weighted Sobolev spaces.

In our setting, we have to face with the well known loss of compactness by concentration, which occurs in every problem with critical growth, even on bounded domains. Indeed, one of the hard part in the proof of the main result of the paper will be devoted to a careful analysis of Palais Smale sequences to understand the consequences of spreading or concentration of mass. For this aim, as discussed before, in order to recover compactness, in the spirit of the celebrated first concentration compactness principle by Lions [27,28,29,30], we have to deal with tight convergence (see also [4]). Roughly speaking, “tightness” tells that the values of the functions should belong, in a suitable integral sense, to some compact set, see Lemma I.1 in [27]. As a consequence, in the second concentration compactness principle it is required the notion of tight convergence for a sequence of measures, which is the weak star convergence of measures in the dual space of bounded functions. We point out that the unbounded case is sensibly more complicated than the bounded case since, only in the latter case, tight convergence of a sequence of measures reduces morally to standard convergence of measures, which is the weak star convergence of measures in the dual space of functions vanishing at infinity. Generally, tight convergence is stronger than standard convergence of measures. For details in this direction, we refer to Sect. 4 based on the book by Fonseca and Leoni [18]. In this context, Lemma 7 is completely new since it contains the proof of the tight convergence in ${\mathbb {R}}^N$ of a sequence of measures connected to $(PS)_c$ sequences for every $c<0$, in the spirit of the nice paper by Swanson and Yu in [42] devoted to the p-Laplacian and essentially with no parameter. In particular, in Lemma 7 we prove tight convergence for all $\lambda >0$ when $p<k<p^*$, while for $\lambda$ small, when $1<k<p$, provided that the weight K is nonnegative.

We are now ready to state our main result, which completes and extends Theorem 1.1 in [22] to the new case (3).

Theorem 1

Let $N\ge 3$ and $1<q<k<p<N$. Assume that V satisfies (1) and furthermore $V>0$ on some open subset $\Omega _V\subset {\mathbb {R}}^{N}$, with $|\Omega _V|>0$.

Let K verify (2). If $\Vert K\Vert _{\infty }$ is sufficiently small, then there exist $\lambda _{*}, \lambda ^{*}>0$, with $\lambda _{*}<\lambda ^{*}$, such that, for all $\lambda \in (\lambda _{*},\lambda ^{*})$, problem $({\mathcal {P}})$ has a sequence of weak solutions with negative energy, that is $E_{\lambda }(u)<0$.

We observe that condition $\Vert K\Vert _{\infty }$ sufficiently small guarantees that $\Vert K\Vert _{\infty }$ satisfies a certain inequality given in (70) so that $\lambda _{*}<\lambda ^{*}$. In particular, since $\lambda ^*=C/\Vert V\Vert _r\cdot \Vert K\Vert _\infty ^{(p-k)/(p^*-p)}$, for some $C=C(p,k,N)>0$, then $\lambda ^*\rightarrow \infty$ when $\Vert K\Vert _{\infty }\rightarrow 0$.

The proof of Theorem 1 is based on concentration compactness principle, on the use of the truncated energy functional and on the theory of Krasnoselskii genus, introduced in [24]. As a standard procedure, we have first to prove the boundedness of (PS)$_c$ sequences, $c\in {\mathbb {R}}$, for $E_\lambda (u)$, which we obtain in Lemma 4 for all k such that $1<k<p^*$. Then, we have to face to the main difficulty of the paper which consists in verifying the compactness Palais Smale condition at level c for $E_\lambda (u)$ when the critical values c are negative, the point were the lack of compactness becomes manifest. To solve this problem, as described before, we have to deal with tight convergence of $(|u_n|^{p^*})_n$. We emphasize that, due to the new condition (3), the qualitative behavior of $E_\lambda (u)$ is completely different with respect to the case treated in [9] and in [22].

The paper is organized as follows. In Sect. 2, we recall some classical definitions as well as some regularity results on $E_\lambda (u)$, while in Sect. 3 we prove some properties of Palais Smale sequences. In Sect. 4 we state the two concentration compactness principles due to Lions in [27] and [29] and, following the book of Fonseca and Leoni [18], we discuss with all details the relation between tight convergence and standard convergence of sequences of measures, including also the statement of Prohorov Theorem; in addition Sect. 4 contains Lemmas 7 and 8, which are the two crucial lemmas for the proof of the main theorem of the paper. The truncated functional is introduced in Sect. 5 and its properties are listed. Finally, the proof of Theorem 1 is developed in Sect. 6 together with the statement of classical theorems useful in the proof, such as Deformation Lemma and some well known properties of the Krasnoselskii genus.

2 Preliminaries

In this section we state some preliminary results, as well as some notations, useful in the proofs of the main theorem of the paper, given in the Sect. 6.

In what follows, we denote with X the reflexive Banach space $D^{1,p}({\mathbb {R}}^N)\cap D^{1,q}({\mathbb {R}}^N)$, where $D^{1,p}({\mathbb {R}}^N)=\{u\in L^{p^{*}}({\mathbb {R}}^N): Du\in L^{p} ({\mathbb {R}}^N)\}$, endowed with the norm

$$\begin{aligned} \Vert u\Vert :=\Vert u\Vert _{X}=\Vert u\Vert _{D^{1,p}({\mathbb {R}}^N)}+\Vert u\Vert _{D^{1,q}({\mathbb {R}}^N)}=\Vert Du\Vert _{p}+\Vert Du\Vert _{q} \end{aligned}$$

(7)

where $\Vert \cdot \Vert _{p}$ is the $L^p$ norm in ${\mathbb {R}}^N$. Furthermore, we denote by S the Sobolev’s constant, i.e

$$\begin{aligned} S=\inf \left\{ \frac{\Vert D u\Vert ^p_{p}}{\Vert u\Vert ^p_{p^{*}}}: u\in D^{1,p}({\mathbb {R}}^N), u\ne 0\right\} . \end{aligned}$$

(8)

We recall that the value S is achieved in $D^{1,p}({\mathbb {R}}^N)$, for details we refer to Appendix A in [17].

Of course, the functional $E_\lambda$ is well defined in X, indeed if $u\in X$, by Hölder’s inequality with the exponents $r=p^*/(p^*-k)$, $r'=p^*/k$, we have

$$\begin{aligned} E_\lambda (u)\le \frac{1}{p}\Vert u\Vert ^p +\frac{1}{q}\Vert u\Vert ^q+\frac{\lambda }{k}\Vert V\Vert _{r}\Vert u\Vert _{p^{*}}^{k}+ \frac{1}{p^*}\Vert K\Vert _\infty \Vert u\Vert _{p^*}^{p^*}<\infty , \end{aligned}$$

thanks to (1) and (2).

The proof of the regularity of $E_\lambda$ is almost standard, but for completeness we include it. Obviously, it is enough to study the regularity of the functionals

$$\begin{aligned} J(u)=\int _{{\mathbb {R}}^N} V|u|^{k}dx\quad \text {and} \quad H(u)=\int _{{\mathbb {R}}^N} K|u|^{p^{*}}dx. \end{aligned}$$

Now, we first analyze the regularity of J.

Lemma 1

If $V\in L^{r}\left( {\mathbb {R}}^N\right)$, then J(u) is weakly continuous on $D^{1,p}({\mathbb {R}}^N)$. Moreover, J(u) is continuously differentiable and $J': D^{1,p}({\mathbb {R}}^N)\rightarrow [D^{1,p}({\mathbb {R}}^N)]'$ is given by

$$\begin{aligned} J'(u)\psi =k\int _{{\mathbb {R}}^N} V|u|^{k-2}u\psi dx, \end{aligned}$$

(9)

for all $\psi \in D^{1,p}({\mathbb {R}}^N)$.

Proof

Let $(u_{n})_{n}\in D^{1,p}({\mathbb {R}}^N)$ such that $u_n \rightharpoonup u$ in $D^{1,p}({\mathbb {R}}^N)$, thus $u_{n}\rightharpoonup u \,\ \text {in} \,\ L^{p^{*}}({\mathbb {R}}^N)$ and $(u_{n})_{n}$ is bounded in $D^{1,p}({\mathbb {R}}^N)$, in $L^{p^{*}}({\mathbb {R}}^N)$ and also $(|u_n|^k)_n$ in $L^{p^{*}/k}({\mathbb {R}}^N)$ since we have $\Vert |u_{n}|^{k}\Vert _{p^{*}/k}=\Vert u_{n}\Vert ^{k}_{p^{*}}$. Furthermore, by the compactness of the embedding,

$$\begin{aligned} u_n\rightarrow u \,\ \text {in} \,\ L^{s}(\omega ),\quad \omega \Subset {\mathbb {R}}^N,\quad 1\le s<p^*. \end{aligned}$$

Consequently, by using an increasing sequence of compact sets whose union is ${\mathbb {R}}^N$ and a diagonal argument, we also have

$$\begin{aligned} u_n(x)\rightarrow u(x) \text{ a.e. } \text{ in } {\mathbb {R}}^N. \end{aligned}$$

(10)

In turn, by Hölder’s inequality, $\Vert V |u_{n}|^{k}\Vert _1\le C\Vert V\Vert _r<\infty$ by (1) so that using Lebesgue dominated convergence Theorem we have

$$\begin{aligned} J(u_n)=\int _{{\mathbb {R}}^N} V|u_{n}|^{k}dx\rightarrow \int _{{\mathbb {R}}^N} V|u|^{k}dx=J(u), \end{aligned}$$

namely, weak continuity holds. In order to prove $J\in C^{1}$ it is enough to show that J has continuous Gâteaux derivative. Let $u, \psi \in D^{1,p}({\mathbb {R}}^N)$ and $0<|t|<1$, it follows

$$\begin{aligned} \frac{J(u+t\psi )-J(u)}{t}=\int _{{\mathbb {R}}^N}V\frac{|u+t\psi |^{k}-|u|^{k}}{t} dx, \end{aligned}$$

(11)

By the mean value Theorem there exists $\lambda \in (0,1)$ such that

$$\begin{aligned} \frac{\bigl ||u+t\psi |^{k}-|u|^{k}\bigr |}{t}=k|u+\lambda t\psi |^{k-1}|\psi | \le k \bigl (|u|^{k-1}|\psi | +|\psi |^{k}\bigr ). \end{aligned}$$

We now use Hölder’s inequality twice with exponents r, $p^{*}/(k-1)$, $p^{*}$ and r, $p^*/k$ respectively, so that

$$\begin{aligned} \int _{{\mathbb {R}}^N}V\bigl (|u|^{k-1}|\psi |+|\psi |^{k}\bigr ) dx \le \Vert V\Vert _{r}\Vert \psi \Vert _{p^{*}}\left( \Vert u\Vert _{p^{*}}^{k-1}+\Vert \psi \Vert _{p^{*}}^{k-1}\right) . \end{aligned}$$

that is $V\bigl (|u|^{k-1}|\psi |+|\psi |^{k}\bigr )\in L^1({\mathbb {R}}^N)$, thus, by letting $t\rightarrow 0$ in (11), thanks to the Lebesgue dominated convergence Theorem, we have that J is Gâteaux differentiable and (9) holds with $'$ in the Gâteaux sense.

In order to check the differentiability of J, it remains to prove continuity of the Gâteaux derivative. Let $u_{n}\rightarrow u$ in $D^{1,p}({\mathbb {R}}^N)$ then, up to subsequences, by (10), $u_n(x)\rightarrow u(x)$ a.e. in ${\mathbb {R}}^N$, furthermore there exists $U\in L^{p^{*}}({\mathbb {R}}^N)$ such that $|u_n(x)|\le U(x)$ a.e. in ${\mathbb {R}}^N$. For simplicity let $W(u)=V|u|^{k-2}u$ and we show that $W(u)\in L^{(p^*)'}({\mathbb {R}}^N)$, indeed

$$\begin{aligned} |W(u)|^{(p^{*})'}= |V|^{(p^{*})'}|u|^{(k-1)(p^{*})'}\le |V|^r+|u|^{p^*}, \end{aligned}$$

where in the last inequality we have applied Young’s inequality with exponents $r/(p^{*})'$ and $(p^*-1)/(k-1)$. Thus,

$$\begin{aligned}&|W(u_n)-W(u)|^{(p^{*})'}\le c ( |W(u_n)|^{(p^{*})'}+|W(u)|^{(p^{*})'})\\&\quad \le c\bigl (|V|^r +|U|^{p^{*}}+|u|^{p^{*}}\bigr ) \in L^1({\mathbb {R}}^N),\quad c>0, \end{aligned}$$

so that by Lebesgue dominated convergence Theorem, we get

$$\begin{aligned} \lim _{n\rightarrow \infty }\int _{{\mathbb {R}}^N}|W(u_n)-W(u)|^{(p^{*})'}dx=0 \end{aligned}$$

(12)

since, $W(u_n(x))\rightarrow W(u(x))$ a.e. in ${\mathbb {R}}^N$, by continuity of W.

Finally, by Hölder’s inequality, for all $\psi \in D^{1,p}({\mathbb {R}}^N)$, we have

$$\begin{aligned} |\bigl (J'(u_n)-J'(u)\bigr )\psi |\le k\int _{{\mathbb {R}}^N} |W(u_n)-W(u)||\psi |dx\le k\Vert W(u_n)-W(u)\Vert _{(p^{*})'} \Vert \psi \Vert _{p^*}, \end{aligned}$$

consequently,

$$\begin{aligned} \Vert J'(u_{n})-J'(u)\Vert _{[D^{1,p}({\mathbb {R}}^N)]'}\le C \Vert W(u_{n})-W(u)\Vert _{(p^{*})'}\rightarrow 0 \end{aligned}$$

as $n\rightarrow \infty$ thanks to (12). Actually, we have proved that for every sequence $u_n\rightarrow u$ in $D^{1,p}({\mathbb {R}}^N)$, there is a subsequence respect to which $J'$ is sequentially continuous, from this it is an elementary exercise to conclude that $J'$ is sequentially continuous in all of $[D^{1,p}({\mathbb {R}}^N)]'$. In turn, $J\in C^{1}$. $\square$

Analogously, it holds the following.

Lemma 2

If $K\in L^{\infty }({\mathbb {R}}^N)$, then H(u) is continuously differentiable in $D^{1,p}({\mathbb {R}}^N)$ and its derivative $H': D^{1,p}({\mathbb {R}}^N)\rightarrow [D^{1,p}({\mathbb {R}}^N)]'$ is given by

$$\begin{aligned} H'(u)\psi =p^{*}\int _{{\mathbb {R}}^N} K|u|^{p^{*}-2}u\psi dx, \end{aligned}$$

for all $\psi \in D^{1,p}({\mathbb {R}}^N)$.

Finally, using the continuity of the embedding $D^{1,p}({\mathbb {R}}^N)\hookrightarrow L^{p^{*}}({\mathbb {R}}^N)$, so that if $u_n\rightarrow u$ in X, that is $u_n\rightarrow u$ $D^{1,p}({\mathbb {R}}^N)$ and in $D^{1,q}({\mathbb {R}}^N)$, then

$$\begin{aligned} u_n\rightarrow u\quad \text {in } L^{p^*}({\mathbb {R}}^N),\qquad Du_n\rightarrow Du \quad \text {in } L^{p}({\mathbb {R}}^N) \text { and in } L^{q}({\mathbb {R}}^N). \end{aligned}$$

Since the first two terms of $E_{\lambda }$ are norms with exponents $p,q>1$, and thanks to Lemmas 1 and 2, then immediately $E_{\lambda }\in C^{1}(X)$, with $E'_\lambda : X\rightarrow X'$ and it results

$$\begin{aligned} \begin{aligned} E'_{\lambda }(u)\psi&=\int _{{\mathbb {R}}^N}|D u|^{p-2}D u D\psi dx+\int _{{\mathbb {R}}^N}|D u|^{q-2} D uD\psi dx \\&\quad -\lambda \int _{{\mathbb {R}}^N}V|u|^{k-2}u\psi dx-\int _{{\mathbb {R}}^N}K|u|^{p^{*}-2}u\psi dx. \end{aligned} \end{aligned}$$

(13)

for all $\psi \in X$.

A weak solution of problem $({\mathcal {P}})$ is a function $u\in X$ such that

$$\begin{aligned} E'_{\lambda }(u)\psi =0\quad \text { for all }\psi \in X, \end{aligned}$$

that is u is a critical point of the functional $E_{\lambda }$ or equivalently, by (13), u satisfies the weak formulation of problem $({\mathcal {P}})$, namely

$$\begin{aligned}&\int _{{\mathbb {R}}^N}|D u|^{p-2}D uD\psi dx+\int _{{\mathbb {R}}^N}| D u|^{q-2}D uD\psi dx\\&\quad =\lambda \int _{{\mathbb {R}}^N}V|u|^{k-2}u\psi dx+\int _{{\mathbb {R}}^N}K|u|^{p^{*}-2}u\psi dx \end{aligned}$$

for all $\psi \in X$.

Now, we present a results about convergence that is also needed in our discussion.

Lemma 3

(Lemma 2.7, [25]) Let $\Omega$ be an open set in ${\mathbb {R}}^N$, $\alpha , \beta$ positive numbers and $a(x,\xi )$ in $C(\Omega \times {\mathbb {R}}^N,{\mathbb {R}}^N)$ such that

• (1) $\alpha |\xi |^{s}\le a(x,\xi )\xi$ for all $(x,\xi )\in \Omega \times {\mathbb {R}}^N$;

• (2) $|a(x,\xi )|\le \beta |\xi |^{s-1}$ for all $(x,\xi )\in \Omega \times {\mathbb {R}}^N$;

• (3) $(a(x,\xi )-a(x,\eta ))(\xi ,\eta )>0$ for all $(x,\xi )\in \Omega \times {\mathbb {R}}^N$ with $\xi \ne \eta$.

Consider $(u_{n})_{n}, u\in W^{1,s}(\Omega )$, $s>1$, then $D u_{n}\rightarrow D u$ in $L^{s}(\Omega )$ if and only if

$$\begin{aligned} \lim _{n\rightarrow \infty }\int _{\Omega }\Big (a(x,D u_{n}(x))-a(x,D u(x))\Big )\Big (D u_{n}(x)-D u(x)\Big )dx=0. \end{aligned}$$

3 On Palais Smale sequences

First, we briefly recall the basic definitions.

Definition 1

Let Y be a Banach space and $E: Y\rightarrow {\mathbb {R}}$ be a differentiable functional. A sequence $(u_{n})_{n}\subset Y$ is called a $(PS)_{c}$ sequence for E if $E(u_{k})\rightarrow c$ and $E'(u_{k})\rightarrow 0$ as $k\rightarrow \infty$. Moreover, we say that E satisfies the $(PS)_{c}$ condition if every $(PS)_{c}$ sequence for E has a converging subsequence in Y.

In the next result, we prove the first main property for $(PS)_{c}$ sequences for the functional $E_{\lambda }(u)$ defined in (6). We point out that here the value k does not satisfies (3), but simply $1<k<p^*$.

Lemma 4

Assume $1<k<p^*$, $1<q<p$. Let (1) and (2) be verified and let $(u_{n})_{n}\subset X$ be a $(PS)_{c}$ sequence for $E_{\lambda }(u)$ defined in (6) for all $c\in {\mathbb {R}}$. Then $(u_{n})_{n}$ is bounded in X.

In particular, if $1<k<p$ and $c<0$, it holds

$$\begin{aligned} \Vert u_n\Vert _{p^*}\le \, C_* \lambda ^{1/(p-k)}, \qquad C_*=\biggl [\frac{N(p^*-k)}{Skp^*}\Vert V\Vert _r\biggr ]^{1/(p-k)}, \end{aligned}$$

(14)

where S is the Sobolev’s constant.

Proof

Let $(u_{n})_{n}\subset X$ be a $(PS)_{c}$ sequence of $E_{\lambda }(u)$ for all $c\in {\mathbb {R}}$ namely, by Definition 1,

$$\begin{aligned} E_{\lambda }(u_{n})=c+o(1), \,\ E'_{\lambda }(u_{n})=o(1)\quad \text {as} \quad n\rightarrow \infty , \end{aligned}$$

so that $|E'_{\lambda }(u_{n})(u_{n})|\le \Vert u_{n}\Vert$ for n large. Now we divide the proof in two cases.

Case $1<k<p$: by (13), thanks to (8) and Hölder’s inequality with exponents r and $r'$ we have

$$\begin{aligned} \begin{aligned} c +o(1) +o(1)\Vert u_{n}\Vert&= E_{\lambda }(u_{n})- \frac{1}{p^{*}}E'_{\lambda }(u_{n})u_{n}\\&\ge \left( \frac{1}{p}-\frac{1}{p^{*}}\right) \Vert D u_n\Vert _p^p+\left( \frac{1}{q}-\frac{1}{p^{*}} \right) \Vert D u_n\Vert _q^q\\&\qquad -\lambda \left( \frac{1}{k}-\frac{1}{p^{*}}\right) S^{-k/p}\Vert V\Vert _r \Vert D u_{n}\Vert ^{k}_{p} \end{aligned} \end{aligned}$$

(15)

where we have used that $V\in L^{r}({\mathbb {R}}^N)$ and $\Vert u\Vert _{p^{*}}S^{1/p}\le \Vert D u\Vert _{p}$ for all $u\in D^{1,p}({\mathbb {R}}^N)$. Consequently, writing explicitly $\Vert \cdot \Vert$ given in (7), we get

$$\begin{aligned} c+\Vert u_{n}\Vert _{D^{1,q}} - c_{2}\Vert u_{n}\Vert _{D^{1,q}}^{q}\ge c_{1}\Vert u_{n}\Vert _{D^{1,p}}^{p} - \lambda c_{3}\Vert u_{n}\Vert _{D^{1,p}}^{k} -\Vert u_{n}\Vert _{D^{1,p}}, \end{aligned}$$

(16)

where $c_{1}, c_{2}, c_{3}$ are positive constants independent of n. From (16) it immediately follows that $\Vert u_n\Vert$ should be bounded, indeed if $\Vert u_{n}\Vert _{D^{1,q}}\rightarrow \infty$ and $(\Vert u_{n}\Vert _{D^{1,p}})_n$ bounded, then by letting $n\rightarrow \infty$ in (16) we obtain a contradiction since the left hand side goes to $-\infty$, being $q>1$ while the right term is bounded. If $\Vert u_{n}\Vert _{D^{1,p}}\rightarrow \infty$ as $n\rightarrow \infty$ and $(\Vert u_{n}\Vert _{D^{1,q}})_{n}$ is bounded, then by letting $n\rightarrow \infty$ in (16) we obtain a contradiction since the right hand side goes to $\infty$, being $p>1$ and $p>k$, while the left term is bounded. Finally if $\Vert u_{n}\Vert _{D^{1,p}}, \Vert u_{n}\Vert _{D^{1,q}}\rightarrow \infty$ then the left hand side of (16) goes to $-\infty$ while the right goes to $\infty$. This last contradiction concludes the proof of the first case.

Case $p\le k<p^*$: arguing as in (15), with $1/p^*$ replaced by 1/k, since $K(x)\ge 0$ in ${\mathbb {R}}^N$, we obtain

$$\begin{aligned} c+\Vert u_{n}\Vert _{D^{1,q}} - c'_{2}\Vert u_{n}\Vert _{D^{1,q}}^{q}\ge c'_{1}\Vert u_{n}\Vert _{D^{1,p}}^{p} -\Vert u_{n }\Vert _{D^{1,p}}, \end{aligned}$$

(17)

where $c'_{1}, c'_{2}$ are positive constants independent of n. From (17), using a similar argument as in the first case, it follows that $\Vert u_n\Vert$ should be bounded in X.

To obtain (14), it is enough to observe that using the boundedness of $(u_n)_n$, from (15), being $c<0$, it follows, for n large, that

$$\begin{aligned} \frac{1}{N}\Vert D u_n\Vert _p^p-\lambda \left( \frac{1}{k}-\frac{1}{p^{*}}\right) S^{-k/p} \Vert V\Vert _r \Vert D u_{n}\Vert ^k_p\le 0, \end{aligned}$$

so that

$$\begin{aligned} \Vert D u_{n}\Vert ^{p-k}_{p}\le \lambda S^{-k/p}\frac{N(p^*-k)}{kp^*}\Vert V\Vert _r, \end{aligned}$$

which yields (14) by virtue of Sobolev’s inequality and for $1<k<p$.

Thus, the proof is completed. $\square$

4 Concentration compactness

Before stating the first concentration compactness lemma due to Lions in [27], we recall, for completeness, some well known notions, following [18]. Let Y be a locally compact Hausdorff space and let $M(Y, {\mathbb {R}})$ be the space of all finite signed Radon measures (cfr. Definitions 1.5, 1.166 and 1.55 in [18]). In this setting, we have

$$\begin{aligned} (C_0(Y))'=M(Y, {\mathbb {R}}), \end{aligned}$$

where $C_0(Y)$ is the space of all continuous functions that vanish at infinity or, equivalently, it is the completion of $C_c(Y)$, i.e. the space of all functions whose support is compact, relative by the supremum norm $\Vert \cdot \Vert _\infty$. First, we recall the definition of the (standard) convergence of measures, also called in some works, [29, 30] and [32], weak convergence of measures.

Definition 2

A sequence of measures $(\mu _n)_n\in M(Y, {\mathbb {R}})$ converges (standard) to a measure $\mu \in M(Y, {\mathbb {R}})$, that is $\mu _n \rightharpoonup \mu$, if for every $\varphi \in C_0(Y)$

$$\begin{aligned} \int _Y \varphi d\mu _n \rightarrow \int _Y \varphi d\mu , \quad \text {as} \quad n\rightarrow \infty . \end{aligned}$$

Equivalently, the (standard) convergence of measures is the weak star convergence of measures respect to $(C_0(Y))'$.

Now, let $C_b(Y)$ be the space of real bounded functions defined in Y and we report the definition of tight convergence of measures in the same setting as above.

Definition 3

A sequence of measures $(\mu _n)_n\in M(Y, {\mathbb {R}})$ converges tightly to a measure $\mu \in M(Y, {\mathbb {R}})$, that is $\mu _n\overset{*}{\rightharpoonup } \mu$, if for every $\varphi \in C_b(Y)$

$$\begin{aligned} \int _Y \varphi d\mu _n \rightarrow \int _Y \varphi d\mu , \quad \text {as} \quad n\rightarrow \infty . \end{aligned}$$

Equivalently, the tight convergence of measures is the weak star convergence respect to $(C_b(Y))'$.

Remark 1

It is known that the dual spaces of $C_c(Y)$ and $C_0(Y)$ coincide, up to isomorphisms, while $(C_b(Y))'$ is larger. Thus, the tight convergence is stronger than the (standard) convergence of measures, unless Y is compact, since in this case $C_0(Y)=C_c(Y)=C_b(Y)$ so that $(C_b(Y))'$ is still the set of signed Radon measures. Of course if Y is only bounded, the above equalities hold for ${\overline{Y}}$. If Y is unbounded, then the dual of $C_b(Y)$ is the space of regular finitely additive signed measures (see Sections 1.3.3 and 1.3.4 in [18]).

Now we are ready to present the first concentration compactness lemma.

Lemma 5

(Lemma I.1, [27]) Let $(\rho _n)_n$ be a sequence in $L^1({\mathbb {R}}^N)$ satisfying

$$\begin{aligned} \rho _n\ge 0 \,\, \text {in} \,\, {\mathbb {R}}^N, \qquad \int _{{\mathbb {R}}^N}\rho _n dx=\Lambda , \end{aligned}$$

where $\Lambda >0$ is fixed. Indeed, up to a subsequence, one of the following three situations hold:

• (a) (Compactness) There exists a sequence $(y_n)_{n}$ in ${\mathbb {R}}^N$ such that $\rho _n(\cdot +y_n)$ is tight that is for any $\varepsilon >0$ there exists $0<R_\varepsilon <\infty$ for which

  $$\begin{aligned} \int _{B_{R_\varepsilon }(y_n)}\rho _n(x) dx \ge \Lambda -\varepsilon \quad \hbox { for all }n\in {\mathbb {N}}\hbox { large}. \end{aligned}$$

• (b) (Vanishing) For all $R>0$ there holds

  $$\begin{aligned} \lim _{n\rightarrow \infty }\left( \sup _{y\in {\mathbb {R}}^N}\int _{B_R(y)}\rho _n(x) dx\right) =0. \end{aligned}$$

• (c) (Dichotomy) There exists $\ell \in (0,\Lambda )$ such that for any $\varepsilon >0$ there exists $n_0\ge 1$ and $0\le \rho _n^1, \rho _n^2\in L^1({\mathbb {R}}^N)$ satisfying for $n\ge n_0$

  $$\begin{aligned}&\int _{{\mathbb {R}}^N} [\rho _n(x)-(\rho _n^1(x)+\rho _n^2(x))]dx\le \varepsilon \\&\biggl | \int _{{\mathbb {R}}^N} \rho _n^1(x) dx -\ell \biggr |\le \varepsilon \\&\biggl | \int _{{\mathbb {R}}^N} \rho _n^2(x) dx -(\Lambda -\ell ) \biggr |\le \varepsilon \\&\text {dist}\bigl (\hbox {Supp}(\rho _n^1), \hbox {Supp}(\rho _n^2)\bigr )\rightarrow \infty \quad \text {as} \quad n\rightarrow \infty . \end{aligned}$$

The following theorem gives a sufficient condition to obtain the tight convergence for a sequence of bounded Borel measures.

Theorem 2

((Prohorov) Theorem 1.208, [18]) Let Y be a metric space and let $(\mu _n)_n$ be a sequence of bounded Borel measure. Assume that for all $\varepsilon >0$ there exists a compact set $K_\varepsilon \subset Y$ such that

$$\begin{aligned} \sup _{n} [\mu _n(Y {\setminus } K_{\varepsilon })]\le \varepsilon . \end{aligned}$$

(18)

Then there exist a subsequence $(\mu _{n_k})_k \subset (\mu _n)_n$ and a Borel measure $\mu$ such that $\mu _{n_k}\overset{*}{\rightharpoonup } \mu$.

Remark 2

From Proposition 1.202 in [18], any sequence of bounded measures admits a subsequence which converges in the sense of Definition 2. Thus, from Theorem 2, to obtain the tight convergence in the sense of Definition 3 we need, in addition to the boundedness of the sequence, that for all $\varepsilon >0$ there exists a compact set $K_\varepsilon$ such that (18) holds. From Lemma 5, the compactness condition (a) assert that, for the translated measures $\mu _n:=\rho _n(y_n+\cdot )$ condition (18) is satisfied, therefore, the sequence of translated measures $(\mu _n)_n$ admits a subsequence which converges tightly.

Now we are ready to state the second concentration compactness lemma.

Lemma 6

(Lemma I.1, [29]) Assume $1\le p< N/m$, $m\ge 1$ and $p^*_m=Np/(N-mp)$, with $p^*_1=p^*$. Let $(u_{n})_{n}$ be a bounded sequence in $D^{m,p}({\mathbb {R}}^N)$ converging weakly to some u and such that $|D^{m}u_{n}|^{p}$ converges weakly to $\mu$ and $|u_{n}|^{p^*_m}$ converges tightly to $\nu$ where $\mu$, $\nu$ are bounded nonnegative measures on ${\mathbb {R}}^N$. Then we have:

• (i) There exist some at most countable set J and two families $(x_{j})_{j\in J}$ of distinct points in ${\mathbb {R}}^N$ and $(\nu _{j})_{j\in J}$ of a positive numbers such that

  $$\begin{aligned} \nu =|u|^{p^*_m}+ \sum _{j\in J}\nu _{j}\delta _{x_{j}}. \end{aligned}$$

  where $\delta _{x}$ is the Dirac-mass of mass 1 concentrated at $x\in {\mathbb {R}}^{N}$.

• (ii) In addition we have

  $$\begin{aligned} \mu \ge |D^{m}u|^{p}+\sum _{j\in J}\mu _{j}\delta _{x_{j}} \end{aligned}$$

  for some $\mu _{j}>0$ satisfying $S\nu _{j}^{p/p^*_m}\le \mu _{j},$ for all j and with S the Sobolev’s constant, hence

  $$\begin{aligned} \sum _{j\in J}\nu _{j}^{p/p^*_m}<\infty . \end{aligned}$$

Thus, to apply Lemma 6, we need that $|u_{n}|^{p^{*}}\overset{*}{\rightharpoonup }\nu$, with $\nu$ bounded nonnegative measure. This property, up to subsequences, follows immediately if we consider a bounded sequence $(u_n)_n$ in $D^{1,p}(\Omega )$ with $\Omega$ bounded, indeed by standard extensions theorems we may assume, without loss of generality that $(u_n)_n\subset D^{1,p}({\mathbb {R}}^N)$ and $|u_{n}|^{p^{*}}\overset{*}{\rightharpoonup }\nu$, by Remarks 1 and 2. Contrarily, in the case of a bounded sequence $(u_n)_n$ in $D^{1,p}({\mathbb {R}}^N)$, to obtain the tight convergence, we need to exclude Vanishing and Dicothomy in Lemma 5.

The following two lemmas are crucial in the proof of Theorem 1, given in Sect. 6.

Lemma 7

Let $1<q<p$. Assume that V and K satisfy (1) and (2). Define, for $1<k<p$,

$$\begin{aligned} {\overline{\lambda }}^*:=S^{(p^*-k)/(p^*-p)}\frac{k}{N} \biggl (\frac{p^*}{p^*-k}\biggr )^{k/p} \biggl (\frac{p}{p-k}\biggr )^{(p-k)/p}\frac{1}{\Vert V\Vert _r\Vert K\Vert _\infty ^{(p-k)/(p^*-p)}}, \end{aligned}$$

where S is the Sobolev’s constant. If $c<0$ and either $p<k<p^*$ and $\lambda \in (0,\infty )$ or

$$\begin{aligned} 1<k<p\quad \text {and}\quad \lambda \in (0, {\overline{\lambda }}^*), \end{aligned}$$

(19)

then every $(PS)_c$ sequence, $(u_n)_n$, for $E_{\lambda }$ is such that, up to subsequences,

$$\begin{aligned} \nu _n=|u_n|^{p^*}dx\overset{*}{\rightharpoonup } \nu , \end{aligned}$$

where $\nu$ is a bounded nonnegative measure.

Proof

Let $(u_{n})_n$ be a (PS)$_{c}$ sequence. Thus, as $n\rightarrow \infty$,

$$\begin{aligned} \frac{1}{p}\Vert D u_n\Vert _p^p+\frac{1}{q}\Vert D u_n\Vert _q^q -\frac{\lambda }{k}\int _{{\mathbb {R}}^N}V|u_n|^{k}dx -\frac{1}{p^{*}}\int _{{\mathbb {R}}^N}K|u_n|^{p^{*}}dx =c+o_n(1) \end{aligned}$$

(20)

and

$$\begin{aligned} \Vert D u_n\Vert _p^p+\Vert D u_n\Vert _q^q -\lambda \int _{{\mathbb {R}}^N}V|u_n|^{k}dx-\int _{{\mathbb {R}}^N}K|u_n|^{p^{*}}dx=\Vert u_n\Vert o_n(1), \end{aligned}$$

(21)

where $o_n(1)\rightarrow 0$ as $n\rightarrow \infty$ and $\Vert \cdot \Vert$ is the norm given in (7). Using Lemma 4, the sequence $(u_{n})_n$ is bounded in X. By Banach Alaoglu Theorem, since X is a reflexive space, there exists $u\in X$ such that, up to subsequences, $u_{n}\rightharpoonup u$ in X,

$$\begin{aligned}&u_{n}\rightharpoonup u \,\ \text {in} \,\ L^{p^{*}}({\mathbb {R}}^N),\quad u_{n}\rightharpoonup u \,\ \text {in} \,\ L^{q^{*}}({\mathbb {R}}^N),\\&D u_{n}\rightharpoonup D u \,\ \text {in} \,\ L^{p}({\mathbb {R}}^N), \quad D u_{n} \rightharpoonup D u \,\ \text {in} \,\ L^{q}({\mathbb {R}}^N). \end{aligned}$$

Moreover, (10) is in force, namely

$$\begin{aligned} u_n(x)\rightarrow u(x) \text{ a.e. } \text{ in } {\mathbb {R}}^N. \end{aligned}$$

Consider the auxiliary sequence of functions $(z_n)_n$, $z_n(x)\ge 0$ in ${\mathbb {R}}^N$ for all $n\in {\mathbb {N}}$, given by

$$\begin{aligned} z_n(x)= |D u_n(x)|^p +|D u_n(x)|^q+|u_n(x)|^{p^*}+\lambda V(x)|u_n(x)|^k. \end{aligned}$$

Define $\eta _n=z_n dx$. We claim that $\eta _n$ converges tightly to a bounded nonnegative measure $\eta$ on ${\mathbb {R}}^N$, that is, $z_n\overset{*}{\rightharpoonup } \eta$. First, we prove that there is $\Lambda >0$ such that

$$\begin{aligned} \lim _{n\rightarrow \infty }\int _{{\mathbb {R}}^N}z_n(x) dx=\Lambda >0 \quad \text {as}\,\,n\rightarrow \infty . \end{aligned}$$

(22)

Indeed, by weak convergence, the sequences $(\Vert Du_n\Vert _p)_n$, $(\Vert u_n\Vert _{p^*})_n$, $(\Vert Du_n\Vert _q)_n$ are bounded so that, by the Bolzano-Weiestrass Theorem, up to subsequences, there exist L, M, $Q \ge 0$ such that

$$\begin{aligned} L=\lim _{n\rightarrow \infty }\Vert Du_n\Vert _p^p,\quad M=\lim _{n\rightarrow \infty }\Vert u_n\Vert _{p^*}^{p^*},\quad Q=\lim _{n\rightarrow \infty }\Vert Du_n\Vert _q^q. \end{aligned}$$

Actually $L,M>0$. Indeed, using (1), (2) and Hölder’s inequality with exponents r and $p^*/k$, we have

$$\begin{aligned} E_\lambda (u_n)\ge \frac{1}{p}\Vert D u_n\Vert _p^p-\frac{\lambda }{k}\Vert V\Vert _r\Vert u_n\Vert _{p^*}^k- \Vert K\Vert _\infty \Vert u_n\Vert _{p^*}^{p^*}. \end{aligned}$$

Hence, if $M=0$, then, by letting $n\rightarrow \infty$, thanks to (20), we arrive to $0\le L/p \le c<0$ which is a contradiction. Thus, $M>0$ and Sobolev’s inequality gives $L>0$.

The continuity of the functional J in $L^{p^*}({\mathbb {R}}^N)$, J given in Lemma 1, implies the existence of the following limit

$$\begin{aligned} \lim _{n\rightarrow \infty }\int _{{\mathbb {R}}^N} V|u_n|^k dx=:H. \end{aligned}$$

(23)

Clearly $H\ge 0$. We claim that $H>0$. Multiplying (20) by $p^*$ and then subtracting (21), we obtain, as $n\rightarrow \infty$,

$$\begin{aligned}&\biggl (\frac{p^*}{p}-1\biggr )\Vert D u_n\Vert _p^{p}+\biggl (\frac{p^*}{q}-1\biggr ) \Vert D u_n\Vert _q^{q}\\&\quad -\lambda \biggl (\frac{p^*}{k}-1\biggr )\int _{{\mathbb {R}}^N}V|u_n|^{k}dx=cp^*+\Vert u_n\Vert o_n(1). \end{aligned}$$

By letting $n\rightarrow \infty$, since $(u_n)_n$ is bounded in X, we get

$$\begin{aligned} \biggl (\frac{p^*}{p}-1\biggr )L+\biggl (\frac{p^*}{q}-1\biggr )Q-\lambda \biggl (\frac{p^*}{k}-1\biggr ) H=cp^*, \end{aligned}$$

since $p, \,q,\, k<p^*$, $\lambda >0$, $L>0$ and $Q\ge 0$, necessarily $H>0$ being $c<0$. Consequently, condition (22) holds with $\Lambda =L+Q+M+\lambda H>0$. We can apply Lemma 5 to the sequence $(z_n)_n$. Hence, up to a subsequence, three situations can occur: Compactness, Vanishing or Dichotomy. In particular, thanks to Theorem 2 (cfr. Remark 2), Compactness is equivalent to tightness so that we have to exclude Vanishing and Dichothomy for the sequence $(z_n)_n$.

We immediately see that Vanishing cannot occur. Indeed from (22), we can assume that there exists $R_1\in (0,\infty )$ such that $\int _{B_{R_1}(0)}z_n(x) dx\ge \Lambda /2>0$, in turn (b) in Lemma 5 fails.

To prove that Dichotomy cannot hold, we argue by contradiction and we assume that there exists $\ell \in (0,\Lambda )$ such that for all $\varepsilon >0$, there exist $R>0$, $\ell \in (0,\Lambda )$, $(R_n)_n$, with $2R<R_n\rightarrow \infty$ and $(y_n)_n$ in ${\mathbb {R}}^N$ such that, for all n large, we get

$$\begin{aligned} \begin{aligned}&\biggl | \int _ {B_{R}(y_n)}z_n(x)dx - \ell \,\biggr |<\varepsilon ,\\&\biggl | \int _ {{\mathbb {R}}^N{\setminus } B_{R_n}(y_n)}z_n(x)dx\, + \ell -\Lambda \biggr |<\varepsilon ,\\&\biggl | \int _ {D_n}z_n(x)dx \, \biggr | <\varepsilon ,\quad D_n=B_{R_n}(y_n){\setminus } B_{R}(y_n). \end{aligned} \end{aligned}$$

(24)

Let $\varphi \in C_c^\infty ({\mathbb {R}}^N)$ be such that $0\le \varphi \le 1$ in ${\mathbb {R}}^N$, $\varphi _{|B_1(0)}\equiv 1$ and $\varphi _{|B_2(0)^c}\equiv 0$. We define $u_n^1=\varphi ^1_n u_n$ and $u_n^2=(1-\varphi ^2_n) u_n$, where

$$\begin{aligned} \varphi ^1_n(x):=\varphi \biggl (\frac{x-y_n}{R}\biggl ),\qquad \varphi ^2_n(x):=\varphi \biggl (\frac{x-y_n}{R_n}\biggl ), \end{aligned}$$

for all $x\in {\mathbb {R}}^N$ and all $n\in {\mathbb {N}}$. Then, $\hbox {Supp}(u_n^1)=\{x\in {\mathbb {R}}^N : |x-y_n|\le 2R\}$ and $\hbox {Supp}(u_n^2)=\{x\in {\mathbb {R}}^N : |x-y_n|\ge R_n\}$ are disjoint sets for every $n\in {\mathbb {N}}$. In addition, $\text{ dist }\bigl (\hbox {Supp}(u_n^1),\,\hbox {Supp}(u_n^2)\bigl )\rightarrow \infty$. In particular, it follows

$$\begin{aligned} \int _{{\mathbb {R}}^N}|D u_n^1|^p\,dx=\int _{B_{R}(y_n)}|D u_n|^p\, dx+\int _{D_n}\bigl [|\varphi _n^1|^p|D u_n|^p + |u_n^1|^p|D \varphi _n^1|^p\bigr ]dx \end{aligned}$$

and

$$\begin{aligned} \int _{{\mathbb {R}}^N}|D u_n^2|^p\,dx=\int _{{\mathbb {R}}^N {\setminus } B_{2R_n}(y_n)}|D u_n|^p\, dx +\int _{D_n}\bigl [(1-\varphi _n^2)^p|D u_n|^p+ |u_n^2|^p|D \varphi _n^2|^p\bigr ]dx. \end{aligned}$$

So that, by (24) and the facts that $\Vert D\varphi ^1_n\Vert _\infty \le c/R$, $\Vert D\varphi ^2_n\Vert _\infty \le c/R_n$, this yields

$$\begin{aligned}&\int _{{\mathbb {R}}^N}|D u_n^1|^p\,dx=\int _{B_{R}(y_n)}|D u_n|^p\, dx+o_\varepsilon (1), \\&\int _{{\mathbb {R}}^N}|D u_n^2|^p\,dx=\int _{{\mathbb {R}}^N {\setminus } B_{2R_n}(y_n)}\!\!|D u_n|^p\, dx +o_\varepsilon (1), \end{aligned}$$

where $o_\varepsilon (1)\rightarrow 0$ as $\varepsilon \rightarrow 0$. Similar formulas hold for $\int _{{\mathbb {R}}^N}|D u_n^i|^q dx$, $i=1,2$. Furthermore, by Hölder’s inequality and (24), we get

$$\begin{aligned} \int _{{\mathbb {R}}^N}V|u_n^1|^{k}dx= & {} \int _{B_{R}(y_n)}\!V|u_n|^{k}dx+o_\varepsilon (1),\\ \int _{{\mathbb {R}}^N}V|u_n^2|^{k}dx= & {} \int _{{\mathbb {R}}^N {\setminus } B_{2R_n}(y_n)}\!\!V|u_n|^{k}dx +o_\varepsilon (1). \end{aligned}$$

Similar formulas hold for $\int _{{\mathbb {R}}^N}K|u_n^i|^{p^{*}} dx$, $i=1,2$. Consequently, (20), (21), (24) give, respectively,

$$\begin{aligned} \begin{aligned}&\sum _{i=1}^2\biggr (\frac{1}{p}\Vert D u_n^i\Vert _p^p+\frac{1}{q}\Vert D u_n^i\Vert _q^q -\frac{\lambda }{k} \int _{{\mathbb {R}}^N}V|u_n^i|^{k}dx\\&\quad -\frac{1}{p^{*}}\int _{{\mathbb {R}}^N}K|u_n^i|^{p^{*}}dx\biggl )=c+o_n(1)+o_\varepsilon (1), \end{aligned} \end{aligned}$$

(25)

and

$$\begin{aligned}&\sum _{i=1}^2\biggr (\Vert D u_n^i\Vert _p^p+\Vert D u_n^i\Vert _q^q -\lambda \int _{{\mathbb {R}}^N}V|u_n^i|^{k}dx- \int _{{\mathbb {R}}^N}K|u_n^i|^{p^{*}}dx\biggl )\nonumber \\&\quad =\sum _{i=1}^2 \Vert u_n^i\Vert o_n(1)+o_\varepsilon (1) \end{aligned}$$

(26)

where we first let $n\rightarrow \infty$ and then $\varepsilon \rightarrow 0$. As above, eventually passing to subsequences, there exist nonnegative limits $\alpha _i, \beta _i$, $i=1,2$, defined by

$$\begin{aligned} \alpha _i=\lim _{n\rightarrow \infty }\int _{{\mathbb {R}}^N}V|u_n^i|^kdx \quad \text {and}\quad \beta _i=\lim _{n\rightarrow \infty }\int _{{\mathbb {R}}^N}K|u_n^i|^{p^*}dx. \end{aligned}$$

Now, replacing the values of $\alpha _i$, $\beta _i$ in (26) we obtain as $n\rightarrow \infty$

$$\begin{aligned} \sum _{i=1}^2 \bigl (\Vert D u_n^i\Vert _p^{p}+\Vert D u_n^i\Vert _q^{q}\bigr )=\sum _{i=1}^2 \bigl ( \lambda \alpha _i+\beta _i+ \Vert u_n^i\Vert o_n(1) \bigr )+o_\varepsilon (1). \end{aligned}$$

Multiplying (25) by q and p, respectively, and then subtracting (26), both evaluated in $u_n^i$, we obtain

$$\begin{aligned} \begin{aligned} \sum _{i=1}^2\Vert D u_n^i\Vert _p^{p}&=\sum _{i=1}^2 \biggl (\lambda \frac{p(q-k)}{k(q-p)} \int _{{\mathbb {R}}^N}V|u_n^i|^{k}+\frac{p(q-p^*)}{p^*(q-p)}\int _{{\mathbb {R}}^N}K|u_n^i|^{p^*}dx\\&\quad +\Vert u_n^i\Vert o_n(1) \biggr )+c\frac{qp}{q-p}+o_\varepsilon (1) \end{aligned} \end{aligned}$$

and

$$\begin{aligned} \begin{aligned} \sum _{i=1}^2\Vert D u_n^i\Vert _q^{q}&=\sum _{i=1}^2 \biggl (\lambda \frac{q(p-k)}{k(p-q)} \int _{{\mathbb {R}}^N}V|u_n^i|^{k}- \frac{q(p^*-p)}{p^*(p-q)}\int _{{\mathbb {R}}^N}K|u_n^i|^{p^*}dx\\&\quad +\Vert u_n^i\Vert o_n(1) \biggr )+c\frac{pq}{p-q} +o_\varepsilon (1), \end{aligned} \end{aligned}$$

from which we deduce, for $n\rightarrow \infty$ e since $\Vert u_n^i\Vert$ is bounded,

$$\begin{aligned} \sum _{i=1}^2\Vert D u_n^i\Vert _p^{p}=\sum _{i=1}^2 \biggl (\lambda \frac{p(q-k)}{k(q-p)}\alpha _i +\frac{p(q-p^*)}{p^*(q-p)}\beta _i\biggr )+c\frac{qp}{q-p}+ o_n(1)+o_\varepsilon (1) \end{aligned}$$

(27)

and

$$\begin{aligned} \sum _{i=1}^2\Vert D u_n^i\Vert _q^{q}=\sum _{i=1}^2 \biggl (\lambda \frac{q(p-k)}{k(p-q)}\alpha _i - \frac{q(p^*-p)}{p^*(p-q)}\beta _i\biggr )+c\frac{pq}{p-q}+o_n(1)+o_\varepsilon (1), \end{aligned}$$

(28)

as $\varepsilon \rightarrow 0$. In particular, since $q<p$ and using that the left hand side is nonnegative, then (27) and (28) give, respectively,

$$\begin{aligned} c\le \biggl (\frac{1}{q}-\frac{1}{p^*}\biggr ) (\beta _1+\beta _2)- \lambda \biggl (\frac{1}{k}-\frac{1}{q} \biggr )(\alpha _1+\alpha _2), \end{aligned}$$

(29)

and

$$\begin{aligned} c\ge \frac{\beta _1+\beta _2}{N}-\lambda \biggl (\frac{1}{k}-\frac{1}{p} \biggr )(\alpha _1+\alpha _2). \end{aligned}$$

(30)

If $q<p<k<p^*$, then (29) is trivial, while (30) cannot occur since $c<0$ but the right hand side is positive being $p<k$. This contradiction proves that, in this case, Compactness holds.

We claim that inequality (30) cannot occur also when $1<k<p$, so that we have covered both cases $q<k<p$ and $1<k\le q<p$. At this aim note that, from (24), it follows either $\alpha _1=0$ or $\alpha _2=0$ depending whether $(y_n)_n$ is unbounded or not. Indeed, if $(y_n)_n$ is unbounded then $\hbox {Supp}(u_n^1)$ reduces to the empty set when $n\rightarrow \infty$, consequently, from

$$\begin{aligned} \int _{B_R(y_n)}V|u_n|^kdx\le \Vert V\Vert _{L^r(B_R(y_n))}\Vert u_n\Vert _{p^*}^{k}\le C\Vert V\Vert _{L^r(B_R(y_n))}, \end{aligned}$$

(31)

where C is the constant obtained from the boundedness of the (PS)$_c$ sequence and thanks to the continuity of the embedding of $D^{1,p}({\mathbb {R}}^N)$ in $L^{p^*}({\mathbb {R}}^N)$, then, thanks to (1) we can apply Lebesgue dominated convergence Theorem to the function $\chi _{B_R(y_n)}V^r$, obtaining

$$\begin{aligned} \begin{aligned} \alpha _1&=\lim _{n\rightarrow \infty }\int _{{\mathbb {R}}^N}V|u_n^1|^kdx=\lim _{n\rightarrow \infty }\int _{B_R(y_n)}V|u_n|^kdx\\&\le C \lim _{n\rightarrow \infty }\Vert V\Vert _{L^r(B_R(y_n))}=0 \end{aligned} \end{aligned}$$

by virtue of $|B_R(y_n)|\rightarrow \emptyset$ when $n\rightarrow \infty$ since $y_n\rightarrow \infty$.

On the other hand, if $(y_n)_n$ is bounded, then arguing as above and noting that in this case $\hbox {Supp}(u_n^2)$ becomes the empty set for $n\rightarrow \infty$, we get $\alpha _2=0$.

First, consider the case $\alpha _2=0$, of course $\alpha _1>0$ since

$$\begin{aligned} \alpha _1+\alpha _2+o(1)=\lim _{n\rightarrow \infty }\int _{{\mathbb {R}}^N} V|u_n|^k dx=H>0. \end{aligned}$$

From (26) with $i=2$, by the definition of $\beta _2$ and Sobolev’s inequality we get, as in [42],

$$\begin{aligned} \begin{aligned} \beta _2+o_\varepsilon (1)&=\lim _{n\rightarrow \infty } \biggl \{ \Vert D u_n^2\Vert _p^p+\Vert D u_n^2\Vert _q^q\biggr \}\ge \lim _{n\rightarrow \infty } \Vert D u_n^2\Vert _p^p\\&\ge S \lim _{n\rightarrow \infty } \Vert u_n^2\Vert _{p^*}^p\ge S \beta _2^{(N-p)/N} \Vert K\Vert _\infty ^{-(N-p)/N}, \end{aligned} \end{aligned}$$

yielding

$$\begin{aligned} \beta _2\ge S^{N/p}\Vert K\Vert _\infty ^{-(N-p)/p}. \end{aligned}$$

(32)

Inserting (32) in (30) and using that $\beta _1\ge 0$, we have

$$\begin{aligned} c\ge \frac{S^{N/p}}{N\Vert K\Vert _\infty ^{(N-p)/p}}- \lambda \alpha _1\biggl (\frac{1}{k}-\frac{1}{p}\biggr ) \end{aligned}$$

which is a contradiction since $c<0$ while the right hand side is nonnegative if $\lambda$ satisfies (19)$_2$ thanks to

$$\begin{aligned} \alpha _1\le \alpha _1+\alpha _2\le \Vert V\Vert _r \lim _{n\rightarrow \infty } \Vert u_n\Vert _{p^*}^k \le \lambda ^{k/(p-k)}\Vert V\Vert _r^{p/(p-k)} \biggl [ \frac{N(p^*-k)}{Sp^*k} \biggr ]^{k/(p-k)}, \end{aligned}$$

where we have used Sobolev’s inequality and (14). In the case $\alpha _1=0$, we can repeat the argument above to reach the required contradiction. The proof of the claim is so concluded, in other words, Compactness holds also in case (19).

Consequently, the first concentration compactness principle guarantees that there exists a sequence $(y_n)_n$ in ${\mathbb {R}}^N$ such that $z_n(\cdot +y_n)$ is tight in the sense of Lemma 5, that is for arbitrary $\varepsilon > 0$ there exists $R=R(\varepsilon )\in (0,\infty )$ with

$$\begin{aligned} \int _{{\mathbb {R}}^N {\setminus } B_{R}(y_n)}z_n(x) dx<\varepsilon , \end{aligned}$$

(33)

so that

$$\begin{aligned} \int _{{\mathbb {R}}^N{\setminus } B_{R}(y_n)}V|u_n|^k dx<\varepsilon \end{aligned}$$

(34)

from the definition of $(z_n)_n$. It must be that $(y_n)_n$ is a bounded sequence otherwise if $y_n\rightarrow \infty$ then

$$\begin{aligned} \lim _{n\rightarrow \infty }\int _{|x-y_n|<R}V|u_n|^k dx=0, \end{aligned}$$

thus, combining the above limit with (34), we arrive to

$$\begin{aligned} \lim _{n\rightarrow \infty }\int _{{\mathbb {R}}^N}V|u_n|^k dx=0, \end{aligned}$$

contradicting $H>0$ in (23).

Hence, we can replace $y_n$ by 0 in (33) to obtain the tightness of $z_n$. Moreover, since

$$\begin{aligned} \int _{{\mathbb {R}}^N {\setminus } B_{R}}|u_n|^{p^*} dx\le \int _{{\mathbb {R}}^N {\setminus } B_{R}}z_n(x) dx <\varepsilon \end{aligned}$$

where $B_R$ is the ball centered at the origin and radius R, we obtain the tightness of $|u_n|^{p^*}$. Finally, we define for all $n\in {\mathbb {N}}$ the measure $\nu _n=|u_n|^{p^*}dx$ on ${\mathbb {R}}^N$ which is nonnegative, bounded since $M>0$, and such that verifies all the assumptions of Theorem 2 thus, it admits a subsequence which converges tightly (cfr. Remark 2) to $\nu$, a bounded non negative measure on ${\mathbb {R}}^N$, that is $\nu _n\overset{*}{\rightharpoonup } \nu$ as claimed. The proof is complete. $\square$

Lemma 8

Let $1<k<p$. If $c<0$ then there exists ${\hat{\lambda }}^*>0$ such that $E_{\lambda }$ satisfies (PS)$_{c}$ condition for all $\lambda \in (0,{\hat{\lambda }}^*]$, where ${\hat{\lambda }}^*$ is defined as follows

$$\begin{aligned} {\hat{\lambda }}^*=S^{(p^*-k)/(p^*-p)} \frac{kp^*}{N(p^*-k)}\cdot \frac{1}{\Vert V\Vert _r\cdot \Vert K\Vert _\infty ^{(p-k)/(p^*-p)}}. \end{aligned}$$

(35)

Proof

Let $(u_{n})_n$ be a (PS)$_{c}$ sequence, clearly $(u_{n})_n$ is bounded in X by Lemma 4. Furthermore, since ${\hat{\lambda }}^{*}<{\overline{\lambda }}^{*}$, then Lemma 7 implies that there exists $u\in X$ such that, up to subsequences, we get

• (I) $u_{n}\rightharpoonup u$ in X,

• (II) Since $Du_{n}\rightharpoonup Du$ in $L^{p}({\mathbb {R}}^N)$ and $Du_{n}\rightharpoonup Du$ in $L^{q}({\mathbb {R}}^N)$, then the sequence of measures $(|Du_n|^pdx+|Du_n|^q dx)_n$ is bounded, thus we have

  $$\begin{aligned} |Du_{n}|^{p}dx+|Du_{n}|^{q}dx\rightharpoonup \mu , \end{aligned}$$

• (III) $(|u_n|^{p^*}dx)_n$ converges tightly to $\nu$,

where $\mu , \nu$ are bounded nonnegative measures on ${\mathbb {R}}^N$. Applying (i) of Lemma 6, there exist at most countable set J, a family $(x_j)_{j\in J}$ of distinct points in ${\mathbb {R}}^N$ and two families $(\nu _j)_{j\in J}, \,(\mu _j)_{j\in J}\in ]0,\infty [$ such that

$$\begin{aligned} \nu= & {} |u|^{p^{*}}+\sum _{j\in J}\nu _{j}\delta _{x_{j}}\nonumber \\ \mu\ge & {} |Du|^{p}+|Du|^q+\sum _{j\in J}\mu _{j}\delta _{x_{j}} \end{aligned}$$

(36)

where $\delta _x$ is the Dirac-mass of mass 1 concentrated at $x\in {\mathbb {R}}^N$, with $\nu _j$ and $\mu _j$ satisfying

$$\begin{aligned} S\nu _{j}^{p/p^{*}}\le \mu _{j}. \end{aligned}$$

(37)

Take a standard cut-off function $\psi \in C_{c}^{\infty }({\mathbb {R}}^N)$, such that $0\le \psi \le 1$ in ${\mathbb {R}}^N$, $\psi =0$ for $|x|>1$, $\psi =1$ for $|x|\le 1/2$. For each index $j\in J$ and each $0<\varepsilon <1$, define

$$\begin{aligned} \psi _{\varepsilon }(x):=\psi \left( \frac{x-x_{j}}{\varepsilon }\right) . \end{aligned}$$

Since $E'_{\lambda }(u_{n})\psi \rightarrow 0$ for all $\psi \in X$ being $(u_{n})_n$ a $(PS)_c$ sequence, choosing $\psi =\psi _{\varepsilon }u_{n}$ in (13) we have, as $n\rightarrow \infty$

$$\begin{aligned} \begin{aligned}&\int _{{\mathbb {R}}^N}u_{n}(|D u_{n}|^{p-2}+|D u_{n}|^{q-2})D u_{n}D\psi _{\varepsilon }dx =\lambda \int _{{\mathbb {R}}^N}V|u_{n}|^{k}\psi _{\varepsilon }dx\\&\quad +\int _{{\mathbb {R}}^N}K |u_{n}|^{p^{*}}\psi _{\varepsilon }dx -\int _{{\mathbb {R}}^N}\left( |D u_{n}|^{p}+|D u_{n}|^{q}\right) \psi _{\varepsilon } dx+o(1). \end{aligned} \end{aligned}$$

(38)

Now, being $(u_{n})_n$ bounded in $L^{p^{*}}({\mathbb {R}}^N)$ then also $(|u_{n}|^{k})_n$ is bounded in $L^{{p^*}/k}({\mathbb {R}}^N)$. Furthermore, since $D^{1,p}({\mathbb {R}}^N)\hookrightarrow \hookrightarrow L^{{p^{*}}/k}(\omega )$ for $\omega \Subset {\mathbb {R}}^N$, being $p^*/k<p^*$, taking for instance $\omega ={\overline{B}}_{\varepsilon }(x_{j})$ and using (10), we have, up to subsequences, $|u_{n}|^{k}\rightarrow |u|^k$ in $L^{{p^{*}}/k}(\omega )$ , $|u_{n}(x)|^{k}\rightarrow |u(x)|^{k}$ a.e. in $\omega$ and there exists $w_1\in L^{{p^{*}}/k}(\omega )$ such that $|u_{n}(x)|^k\le w_1(x)$ a.e. in $\omega$. Thus, $V|u_{n}|^{k}\psi _{\varepsilon }\le V w_1\in L^{1}(\omega )$ a.e. in $\omega$ and in turn by the Lebesgue dominated convergence Theorem, we get

$$\begin{aligned} \lim _{n\rightarrow \infty }\int _{{\mathbb {R}}^N}V|u_{n}|^{k}\psi _{\varepsilon }dx= \int _{{\mathbb {R}}^N}V|u|^{k}\psi _{\varepsilon }dx. \end{aligned}$$

(39)

Consequently, using (II), (III) and (39) in (38), we obtain

$$\begin{aligned} \begin{aligned}&\lim _{n\rightarrow \infty }\left( \int _{{\mathbb {R}}^N}u_{n}|D u_{n}|^{p-2}D u_{n}D\psi _{\varepsilon }dx +\int _{{\mathbb {R}}^N}u_{n}|D u_{n}|^{q-2}D u_{n}D\psi _{\varepsilon }dx\right) \\&\quad =\lambda \int _{{\mathbb {R}}^N}V|u|^{k}\psi _{\varepsilon }dx+\int _{{\mathbb {R}}^N}K\psi _{\varepsilon } d\nu -\int _{{\mathbb {R}}^N}\psi _{\varepsilon }d\mu . \end{aligned} \end{aligned}$$

(40)

From Hölder’s inequality, we have

$$\begin{aligned} \begin{aligned}&\left| \int _{{\mathbb {R}}^N}u_{n}|D u_{n}|^{p-2}D u_{n}D\psi _{\varepsilon }dx\right| \le \left\| D u_{n}\right\| _{p}^{p-1}\left( \int _{{\mathbb {R}}^N} |u_{n}|^{p} |D\psi _{\varepsilon }|^{p} dx \right) ^{1/p}\\&\quad \le \Vert u_n\Vert ^{p-1}\left( \int _{B_{\varepsilon }(x_{j})} |u_{n}|^{p} |D\psi _{\varepsilon }|^{p} dx \right) ^{1/p}. \end{aligned} \end{aligned}$$

(41)

Furthermore, arguing as above and since $D^{1,p}({\mathbb {R}}^N)\hookrightarrow \hookrightarrow L^{p}(\omega )$ for $\omega \Subset {\mathbb {R}}^N$, being $p<p^*$, then taking for instance $\omega ={\overline{B}}_{\varepsilon }(x_{j})$, we have $u_n\rightarrow u$ in $L^{p}(\omega )$, $u_n(x)\rightarrow u(x)$ a.e. in $\omega$, up to subsequences, and there exists $w_2\in L^p(\omega )$ such that $|u_{n}(x)|\le w_2(x)$ a.e. in $\omega$. Thus, $|u_n(x) D\psi _{\varepsilon }(x)|\le C w_2(x)$ a.e. in $\omega$, as well as in ${\mathbb {R}}^N$, and in turn, Lebesgue dominated convergence Theorem gives

$$\begin{aligned} |u_{n}D\psi _{\varepsilon }|\rightarrow |uD\psi _{\varepsilon }| \ \text {in} \ L^{p}({\mathbb {R}}^N). \end{aligned}$$

(42)

Consequently, passing to the limit for $n\rightarrow \infty$ in (41), using the boundedness of $(u_n)_n$, Hölder’s inequality with exponents $N/(N-p)$ and N/p, we obtain, thanks to (42),

$$\begin{aligned} \begin{aligned}&\lim _{n\rightarrow \infty }\left| \int _{{\mathbb {R}}^N}u_{n}|D u_{n}|^{p-2}D u_{n}D\psi _{\varepsilon }dx\right| \le C\left( \int _{B_{\varepsilon }(x_{j})}|u|^{p}|D\psi _{\varepsilon }|^{p}dx\right) ^{1/p}\\&\quad \le C\left( \int _{B_{\varepsilon }(x_{j})}|u|^{p^*}dx\right) ^{1/p^*} \left( \int _{B_{\varepsilon } (x_{j})}|D\psi _{\varepsilon }|^{N}dx\right) ^{1/N}\\&\quad \le C\left( \int _{B_{\varepsilon }(x_{j})}|u|^{p^{*}}dx\right) ^{1/p^{*}}, \end{aligned} \end{aligned}$$

(43)

where in the last inequality we have used the properties of $\psi _{\varepsilon }$. Similarly, by replacing p with q, we gain

$$\begin{aligned} \lim _{n\rightarrow \infty }\left| \int _{{\mathbb {R}}^N}u_{n}|D u_{n}|^{q-2}D u_{n}D\psi _{\varepsilon }dx\right| \le C\left( \int _{B_{\varepsilon }(x_{j})}|u|^{q^{*}}dx\right) ^{1/q^{*}}. \end{aligned}$$

In turn, by letting $\varepsilon \rightarrow 0$ and then $n\rightarrow \infty$, being $u\in L^{p^{*}}({\mathbb {R}}^N)\cap L^{q^{*}}({\mathbb {R}}^N)$, we obtain

$$\begin{aligned} \int _{{\mathbb {R}}^N}u_{n}|D u_{n}|^{p-2}D u_{n}D\psi _{\varepsilon }dx\rightarrow 0, \qquad \int _{{\mathbb {R}}^N} u_{n}|D u_{n}|^{q-2}D u_{n}D\psi _{\varepsilon }dx\rightarrow 0, \end{aligned}$$

and, arguing as in (31),

$$\begin{aligned} \int _{{\mathbb {R}}^N}V|u_{n}|^{k}\psi _{\varepsilon }dx\le \int _{B_{\varepsilon }(x_{j})}V|u_{n}|^{k}dx\rightarrow 0 \quad \text {as} \quad \varepsilon \rightarrow 0. \end{aligned}$$

Hence, from (40), if $\varepsilon \rightarrow 0$ we deduce

$$\begin{aligned} K(x_{j})\nu _{j}=\mu _{j}. \end{aligned}$$

(44)

This equality establishes that the concentration of the measure $\mu$ cannot occur at points where $K(x_{j})=0$, moreover, combining (44) and (37), then $S\nu _j^{p/p^*-1}\le K(x_j)$, in particular, $\nu _{j}=0$ if $K(x_{j})=0$, so that the measure $\nu$ cannot concentrate in those points. Hence the set $X_J:=\{x_j: j\in J\}$ does not contain the points $x_{j}$ which are zeros for K.

Let $J_2:=\{j\in J: K(x_j)>0\}$, we claim that $J_2=\emptyset$. From (37) and (44), it follows,

$$\begin{aligned} \nu _{j}\ge \left( \frac{S}{K(x_{j})}\right) ^{N/p}\ge \left( \frac{S}{\Vert K\Vert _\infty }\right) ^{N/p},\qquad j\in J_2. \end{aligned}$$

(45)

To prove the claim, we show that (45) cannot occur for $\lambda$ belonging to a suitable interval. We first note that condition (45) forces that $|J_2|<\infty$ being $\nu$ a bounded measure, indeed, integrating (36), we get, thanks to (45),

$$\begin{aligned} \infty >\int _{{\mathbb {R}}^N}d\nu =\Vert u_n\Vert _{p^*}^{p^*}+\int _{\{x_j\}}\sum _{j\in J_2}\nu _j\delta _{x_j}dx \ge \Vert u_n\Vert _{p^*}^{p^*}+\left( \frac{S}{\Vert K\Vert _\infty }\right) ^{N/p}|J_2|. \end{aligned}$$

On the other hand, $q<p$ forces $1/q-1/p^*>1/N$ and using that $0\le \psi _\varepsilon \le 1$, thanks to (14) and (15), we get

$$\begin{aligned} \begin{aligned} 0>c+o(1)\Vert u_{n}\Vert&\ge \frac{1}{N}\int _{{\mathbb {R}}^N}\bigl (|D u_{n}|^{p}+|D u_{n}|^{q}\bigr )\psi _\varepsilon dx -\lambda \frac{p^{*}-k}{kp^{*}}\Vert V\Vert _{r}\Vert u_{n}\Vert _{p^{*}}^{k}\\&\ge \frac{1}{N}\int _{B_\varepsilon (x_j)}\bigl (|D u_{n}|^{p}+|D u_{n}|^{q}\bigr )dx\,-(C_*)^k\,\frac{p^{*}-k}{kp^{*}}\Vert V\Vert _{r}\lambda ^{p/(p-k)}, \end{aligned} \end{aligned}$$

so that, letting $n\rightarrow \infty$ and using (II), (44) and (45), we arrive to

$$\begin{aligned} 0>c\ge \frac{1}{N}\mu _j- C\lambda ^{p/(p-k)}\ge \frac{1}{N}S^{N/p}\Vert K\Vert _{\infty }^{(p-N)/p}- C\lambda ^{p/(p-k)}, \end{aligned}$$

(46)

where

$$\begin{aligned} C=\left( \frac{N}{S}\right) ^{k/(p-k)} \left( \frac{\Vert V\Vert _r(p^*-k)}{kp^{*}}\right) ^{p/(p-k)}. \end{aligned}$$

If $\lambda \in (0,{\hat{\lambda }}^*]$, then (46) produces the required contradiction, so that $J_2=\emptyset$, concluding the proof of the claim.

On the other hand, a possible concentration at infinity is refused by tightness but, for completeness, we give the proof of it following the idea of Chabrowski in [8] and Ben-Naoum et. al in [4]. Let $R>0$ and define

$$\begin{aligned} \nu _{\infty }:= & {} \lim _{R\rightarrow \infty }\limsup _{n\rightarrow \infty }\int _{|x|>R}|u_{n}|^{p^{*}}dx,\\ \mu _{\infty }:= & {} \lim _{R\rightarrow \infty }\limsup _{n\rightarrow \infty }\int _{|x|>R}\left( |D u_{n}|^{p}+|D u_{n}|^{q}\right) dx. \end{aligned}$$

It is clear that $\nu _{\infty }$ and $\mu _{\infty }$ both exist and are finite. Now we claim that the analogous of (37) holds, precisely

$$\begin{aligned} S\nu _{\infty }^{p/p^{*}}\le \mu _{\infty }. \end{aligned}$$

(47)

Take, as before, another cut off function $\psi _{R}\in C^{\infty }({\mathbb {R}}^N)$ such that $0\le \psi _{R}\le 1$ in ${\mathbb {R}}^{N}$, $\psi _R(x)=0$ for $|x|<R$ and $\psi _{R}(x)=1$ for $|x|>2R$. By (8) we can write

$$\begin{aligned} \begin{aligned} S^{1/p}\left( \int _{{\mathbb {R}}^N }|u_n|^{p^*}|\psi _R|^{p^{*}}dx\right) ^{1/p^{*}}&\le \left( \int _{{\mathbb {R}}^N }\left( |Du_n|^{p}+|Du_n|^{q}\right) |\psi _R|^{p}dx\right) ^{1/p}\\&\quad + \left( \int _{{\mathbb {R}}^N }|u_n|^{p}|D\psi _R|^{p}dx\right) ^{1/p} \end{aligned} \end{aligned}$$

(48)

where we used $(a+b)^{\alpha }\le c(a^{\alpha }+b^{\alpha })$ first with $\alpha =p>1$ and then with $\alpha =1/p<1$.

On the other hand, by the properties of $\psi _R$, we obtain

$$\begin{aligned} \int _{|x|>2R}|D u_{n}|^pdx\le \int _{{\mathbb {R}}^N}|D u_{n}|^p\psi _{R}^{p}dx\le \int _{|x|>R}|D u_{n}|^pdx \end{aligned}$$

and similar inequalities hold for $|D u_{n}|^q$ and $|u_{n}|^{p^{*}}$ for all $n\in {\mathbb {N}}$. Consequently, by using the definitions of $\nu _\infty$ and $\mu _\infty$, we immediately deduce

$$\begin{aligned} \lim _{R\rightarrow \infty }\limsup _{n\rightarrow \infty }\int _{{\mathbb {R}}^N}\left( |D u_{n}|^{p}+|D u_{n}|^{q}\right) \psi _{R}^{p}dx =\mu _{\infty } \end{aligned}$$

(49)

and

$$\begin{aligned} \lim _{R\rightarrow \infty }\limsup _{n\rightarrow \infty }\int _{{\mathbb {R}}^N}|u_{n}|^{p^*}|\psi _{R}|^{p^{*}}dx=\nu _{\infty }, \end{aligned}$$

(50)

while, from $\hbox {Supp}(D\psi _{R})=B_{2R}{\setminus } B_R$, we get

$$\begin{aligned} \lim _{R\rightarrow \infty }\limsup _{n\rightarrow \infty }\left( \int _{{\mathbb {R}}^N}|u_{n}|^p|D\psi _{R}|^p dx\right) ^{1/p}=0. \end{aligned}$$

(51)

In turn, replacing in (48), inequalities (49), (50) and (51), we arrive to (47).

Then, from $E'_{\lambda }(u_{n})\psi \rightarrow 0$ for all $\psi \in X$ as $n\rightarrow \infty$ being $(u_{n})_{n}$ a $(PS)_c$ sequence, choosing $\psi =\psi _R u_n$ in (13), we get

$$\begin{aligned} \begin{aligned}&\int _{R<|x|<2R}u_n\bigl ([D u_{n}|^{p-2} +|D u_{n}|^{q-2}\bigr ) Du_nD\psi _{R}dx =\lambda \int _{|x|>R}V|u_{n}|^{k}\psi _{R}dx\\&\quad +\int _{|x|>R}K|u_{n}|^{p^{*}}\psi _{R}dx -\int _{|x|>R}\bigl (|D u_{n}|^{p}+|D u_{n}|^{q}\bigr )\psi _{R}dx+o(1), \end{aligned} \end{aligned}$$

(52)

as $n\rightarrow \infty$. Similarly to the proof of (43), we have

$$\begin{aligned} \limsup _{n\rightarrow \infty }\left| \int _{{\mathbb {R}}^N}u_{n}|D u_{n}|^{p-2}D u_{n}D\psi _{R}dx\right| \le C \left( \int _{R<|x|<2R}|u|^{p^{*}}dx\right) ^{1/p^{*}}, \end{aligned}$$

and

$$\begin{aligned} \limsup _{n\rightarrow \infty }\left| \int _{{\mathbb {R}}^N}u_{n}|D u_{n}|^{q-2}D u_{n}D\psi _{R}dx\right| \le C \left( \int _{R<|x|<2R}|u|^{q^{*}}dx\right) ^{1/q^{*}}, \end{aligned}$$

so that, using that $u\in L^{p^*}({\mathbb {R}}^N)\cap L^{q^*}({\mathbb {R}}^N)$, from (52) we obtain

$$\begin{aligned} \lim _{R\rightarrow \infty }\limsup _{n\rightarrow \infty }\left\{ \lambda \int _{{\mathbb {R}}^N}V|u_{n}|^{k}\psi _{R}dx+ \int _{{\mathbb {R}}^N}K|u_{n}|^{p^{*}}\psi _{R}dx\right\} =\mu _{\infty }. \end{aligned}$$

(53)

Furthermore, we have

$$\begin{aligned} \lim _{R\rightarrow \infty }\limsup _{n\rightarrow \infty }\int _{{\mathbb {R}}^N}V|u_{n}|^{k}\psi _{R}dx \le \lim _{R\rightarrow \infty }\limsup _{n\rightarrow \infty }\Vert V\Vert _{L^r(|x|>R)}\Vert u_n\Vert ^k_{L^{p^*}(|x|>R)}= 0, \end{aligned}$$

(54)

being $(u_n)_n$ bounded in $L^{p^{*}}({\mathbb {R}}^N)$ and by definition of $\nu _\infty$, we gain

$$\begin{aligned} \lim _{R\rightarrow \infty }\limsup _{n\rightarrow \infty }\left\{ \int _{{\mathbb {R}}^N}K|u_{n}|^{p^{*}}\psi _{R}dx\right\} \le \Vert K\Vert _{\infty }\nu _{\infty }. \end{aligned}$$

(55)

Thanks to (47), (53), (54) and (55) we have so obtained

$$\begin{aligned} \Vert K\Vert _{\infty }\nu _{\infty }\ge \mu _{\infty }\ge S \nu _{\infty }^{p/p^*}. \end{aligned}$$

Reasoning as above, we deduce that concentration at infinity cannot occur if $\lambda \in (0,\hat{\lambda ^*}]$.

Consequently

$$\begin{aligned} \lim _{n\rightarrow \infty }\int _{{\mathbb {R}}^N}|u_{n}|^{p^{*}}dx=\int _{{\mathbb {R}}^N}|u|^{p^{*}}dx. \end{aligned}$$

Furthermore, since $u_n(x)\rightarrow u(x)$ a.e. in ${\mathbb {R}}^N$ from (10), then Brezis Lieb Lemma in [5], implies

$$\begin{aligned} \lim _{n\rightarrow \infty }\int _{{\mathbb {R}}^N}|u_{n}-u|^{p^{*}}dx=0, \end{aligned}$$

thus

$$\begin{aligned} \lim _{n\rightarrow \infty }\int _{{\mathbb {R}}^N}K|u_{n}|^{p^{*}-1}|u_{n}-u|dx=0, \end{aligned}$$

(56)

since $(u_{n})_{n}$ is bounded in X and

$$\begin{aligned} 0\le \int _{{\mathbb {R}}^N}K|u_{n}|^{p^{*}-1}|u_{n}-u|dx \le \Vert K\Vert _{\infty }\Vert u_{n}\Vert _{p^{*}}^{p^{*}-1}\left( \int _{{\mathbb {R}}^N}|u_{n}-u|^{p^{*}}dx\right) ^{1/p^{*}}. \end{aligned}$$

A similar argument shows that

$$\begin{aligned} \lim _{n\rightarrow \infty }\int _{{\mathbb {R}}^N}V|u_{n}|^{k-1}|u_{n}-u|dx=0. \end{aligned}$$

(57)

Now we define

$$\begin{aligned} <A_{p}(u), \varphi >=\int _{{\mathbb {R}}^N}|D u|^{p-2}D uD\varphi dx, \end{aligned}$$

for all $u,\varphi \in X$. Using (13) with $\psi =u_n-u$, we have

$$\begin{aligned} \begin{aligned}&\lim _{n\rightarrow \infty }\biggl [<A_{p}(u_{n}), u_{n}-u>+<A_{q}(u_{n}), u_{n}-u>\\&\quad -\lambda \int _{{\mathbb {R}}^N}V|u_{n}|^{k-2}u_{n}(u_{n}-u)dx-\int _{{\mathbb {R}}^N} K|u_{n}|^{p^{*}-2}u_{n}(u_{n}-u)dx\biggr ]=0, \end{aligned} \end{aligned}$$

so that, by (56) and (57),

$$\begin{aligned} \lim _{n\rightarrow \infty }\bigl [\langle A_{p}(u_{n}), u_{n}-u \rangle +\langle A_{q}(u_{n}), u_{n}-u\rangle \bigr ]=0. \end{aligned}$$

(58)

Using the monotonicity of $A_{q}$, see [19], we have

$$\begin{aligned} \langle A_{p}(u_{n})+A_{q}(u), u_{n}-u \rangle \,\,\le \,\,\langle A_{p}(u_{n})+A_{q}(u_{n}), u_{n}-u \rangle , \end{aligned}$$

thus, applying the limsup to both terms and using (58) we get

$$\begin{aligned} \limsup _{n\rightarrow \infty }\bigl [ \langle A_{p}(u_{n}), u_{n}-u \rangle + \langle A_q(u), u_{n}-u \rangle \bigr ]\le 0 \end{aligned}$$

(59)

Since $u_{n}\rightharpoonup u$ in $D^{1,q}({\mathbb {R}}^N)$, then $\langle A_q(u), u_{n}-u \rangle \rightarrow 0$ as $n\rightarrow \infty$, in turn (59) gives

$$\begin{aligned} \limsup _{n\rightarrow \infty } \langle A_{p}(u_{n}), u_{n}-u \rangle \le 0. \end{aligned}$$

(60)

On the other hand, using the monotonicity of $A_{p}$ and the definition of weak convergence, we obtain, thanks to (60),

$$\begin{aligned} 0\le \limsup _{n\rightarrow \infty }\langle A_{p}(u_{n})-A_{p}(u), u_{n}-u \rangle =\limsup _{n\rightarrow \infty } \langle A_{p}(u_{n}), u_{n}-u\rangle \le 0 \end{aligned}$$

which gives

$$\begin{aligned} \lim _{n\rightarrow \infty }\langle A_{p}(u_{n})-A_{p}(u), u_{n}-u \rangle =0. \end{aligned}$$

(61)

The same argument holds for $A_{q}$. Thus, by virtue of Lemma 3 applied with $a(x,\xi )=|\xi |^{p-2}\xi$, condition (61) is equivalent to

$$\begin{aligned} \lim _{n\rightarrow \infty }\int _{{\mathbb {R}}^N}|D(u_{n}-u)|^{p}dx=0, \quad \lim _{n\rightarrow \infty }\int _{{\mathbb {R}}^N}|D(u_{n}-u)|^{q}dx=0, \end{aligned}$$

that is the strong convergence in $L^p({\mathbb {R}}^N)$ and in $L^q({\mathbb {R}}^N)$ of the sequence $(D u_n)_n$. In turn, by Sobolev Gagliardo Niremberg’s inequality, we obtain the required property, namely $E_\lambda (u)$ satisfies $(PS)_c$ condition for every $c<0$. The proof is complete. $\square$

5 The truncated functional

In this section, for all $1<k<p$, we define $E_\infty$, the truncated functional of $E_\lambda$. First, by Hölder’s and Sobolev’s inequalities we have, for all $u\in X$,

$$\begin{aligned} E_{\lambda }(u)\ge \frac{1}{p}\Vert u\Vert ^{p}_{D^{1,p}}-\lambda c_{1}\Vert u\Vert ^{k}_{D^{1,p}}- c_{2}\Vert u\Vert ^{p^{*}}_{D^{1,p}}. \end{aligned}$$

where $c_1=S^{-k/p}\Vert V\Vert _r/k$ and $c_2=S^{-p^*/p}\Vert K\Vert _\infty /p^*$.

Define $h(t)=t^{p}/p-\lambda c_{1}t^{k}-c_{2}t^{p^{*}}$ in ${\mathbb {R}}_0^+$ and write

$$\begin{aligned} h(t)=t^k{\hat{h}}(t),\qquad {\hat{h}}(t):= -\lambda c_{1} + \frac{1}{p}t^{p-k}-c_{2}t^{p^{*}-k}, \end{aligned}$$

in turn ${\hat{h}}(0)<0$, ${\hat{h}}(t)\rightarrow -\infty$ as $t\rightarrow \infty$ and ${\hat{h}}'(t)>0$ for $t>0$ close to 0. Thus, there exists $T>0$ such that

$$\begin{aligned} {\hat{h}}'(T)=0, \qquad T= \biggl [\frac{p-k}{c_2p(p^*-k)}\biggr ]^{1/(p^*-p)}. \end{aligned}$$

If ${\hat{h}}(T)>0$, there exist $T_{0}$ and $T_{1}$, with $0<T_{0}<T<T_{1}$ such that ${{\hat{h}}}(T_{0})={{\hat{h}}}(T_{1})=0$. Let

$$\begin{aligned} \lambda ^*=S^{(p^*-k)/(p^*-p)} \frac{k(p^*-p)}{p(p^*-k)}\biggl (\frac{p^*(p-k)}{p(p^*-k)}\biggr )^{(p-k)/(p^*-p)} \cdot \frac{1}{\Vert V\Vert _r\cdot \Vert K\Vert _\infty ^{(p-k)/(p^*-p)}}, \end{aligned}$$

(62)

then if $\lambda <\lambda ^*$, it holds

$$\begin{aligned} {\hat{h}}(T)=(p^*-p)\biggl (\frac{p-k}{c_2}\bigg )^{(p-k)/(p^*-p)}\biggl (\frac{1}{p(p^*-k)}\bigg )^{(p^*-k)/(p^*-p)} -\lambda c_1>0, \end{aligned}$$

so that, since $h(T_{0})=h(T_{1})=0$, being $h(t)=t^k{\hat{h}}(t)$, we have

$$\begin{aligned} h(t)>0, \,\, \text {in}\,\, (T_0,T_1), \qquad h(t)\le 0, \,\ \text {in} \, [0, T_{0}] \cup [T_1,\infty ), \end{aligned}$$

cfr. Figure 1. In particular, we have $\lambda ^*<{\hat{\lambda }}^*$, with ${\hat{\lambda }}^*$ given in (35), since

$$\begin{aligned} \frac{kp^*}{N(p^*-k)}>\frac{k(p^*-p)}{p(p^*-k)}\biggl (\frac{p^*(p-k)}{p(p^*-k)}\biggr )^{(p-k)/(p^*-p)} \end{aligned}$$

which is equivalent to

$$\begin{aligned} 1>\frac{N(p^*-p)}{p^* p}\biggl (\frac{p^*(p-k)}{p(p^*-k)}\biggr )^{(p-k)/(p^*-p)}, \end{aligned}$$

but $N(p^*-p)/p^* p=1$, hence the above inequality reduces to ${p^*(p-k)}/{p(p^*-k)}<1$ which trivially holds, being $p^*>p$.

Fig. 1

h(t)

Next, take a cutoff function $\tau \in C^{\infty }({\mathbb {R}}_0^+)$, nonincreasing and such that $\tau (t)=1$ if $0\le t\le T_{0}$ and $\tau (t)=0$ if $t\ge T_{1}$. We consider the truncated functional

$$\begin{aligned} E_{\infty }(u)=\frac{1}{p}\Vert D u\Vert _p^{p}+\frac{1}{q}\Vert D u\Vert _q^{q}-\frac{\lambda }{k}\int _{{\mathbb {R}}^N}V|u|^{k}dx -\frac{\tau \left( \Vert u\Vert _{D^{1,p}}\right) }{p^{*}} \int _{{\mathbb {R}}^N}K|u|^{p^{*}}dx \end{aligned}$$

and define

$$\begin{aligned} {\overline{h}}(t)=\frac{1}{p}t^{p}-\lambda c_{1}t^{k}-c_{2}t^{p^{*}}\tau (t),\quad t\in {\mathbb {R}}_0^+, \end{aligned}$$

then ${\overline{h}}(t)\rightarrow \infty$ as $t\rightarrow \infty$ and ${\overline{h}} (t)\ge h(t)$ for all $t\ge 0$ so that

$$\begin{aligned} \begin{aligned} {\overline{h}} (t)&=h(t) \text { in } (0, T_{0}),\,\,\, {\overline{h}} (T_0)={\overline{h}} (T_0)=0, \,\,\,\\ {\overline{h}}(t)&\ge h(t)>0 \text { in } (T_{0},T_{1}),\,\,\, {\overline{h}}(T_1)>0, \end{aligned} \end{aligned}$$

(63)

furthermore, ${\overline{h}}(t)>0$ in $(T_{1},\infty )$ since, for $t\ge T_1$, it holds ${\overline{h}}(t)=t^k\kappa (t)$ with $\kappa (t)=\frac{1}{p}t^{p-k}-\lambda c_{1}$ which is strictly increasing and positive in $(T_{1},\infty )$, cfr. Fig. 2.

Fig. 2

${\overline{h}}(t)$

Thus, $E_{\infty }(u)\ge {\overline{h}}\left( \Vert u\Vert _{D^{1,p}}\right)$ for all $u\in X$ and

$$\begin{aligned} E_{\lambda }(u)=E_{\infty }(u) \quad \text {if}\quad 0\le \Vert u \Vert _{D^{1,p}}\le T_{0}. \end{aligned}$$

(64)

Furthermore, by the regularity both of $\tau$ and of $E_\lambda$ it follows that $E_{\infty }(u)\in C^{1}(X,{\mathbb {R}})$.

Lemma 9

Let $E_{\infty }$ be the truncated functional of $E_\lambda$.

• (a) If $E_{\infty }(u)<0$, then $\Vert u\Vert _{D^{1,p}}<T_{0}$ and $E_{\lambda }(v)=E_{\infty }(v)$ for all v in a small enough neighborhood of u.

• (b) For all $\lambda \in (0,\lambda ^{*})$, $E_{\infty }(u)$ satisfies the $(PS)_{c}$ condition for $c<0$.

Proof

We prove (a) by contradiction. If $\Vert u\Vert _{D^{1,p}}\in [T_{0},\infty )$, by the above analysis we see that

$$\begin{aligned} E_{\infty }(u)\ge {\overline{h}}\left( \Vert u\Vert _{D^{1,p}}\right) \ge 0. \end{aligned}$$

This contradicts $E_{\infty }(u)<0$, thus $\Vert u\Vert _{D^{1,p}}<T_{0}$ and the last part of (a) is a consequence of the continuity of $E_{\infty }$ and (63)$_1$.

About claim (b), if $c<0$ and $(u_n)_n\subset X$ is a $(PS)_{c}$ sequence of $E_{\infty }$, then we may assume that $E_{\infty }(u_n)<0$ and $E'_{\infty }(u_n)\rightarrow 0$ as $n\rightarrow \infty$. By (a), we have $\Vert u_n\Vert _{D^{1,p}}<T_0$, so that $E_{\infty }(u_n)=E_{\lambda }(u_n)$ and $E'_{\infty }(u_n)=E'_{\lambda }(u_n)$. By Lemma 8, since $\lambda ^*<\hat{\lambda ^*}$, $E_{\lambda }$ satisfies $(PS)_{c}$ condition for $c<0$, thus there is a convergent subsequence $(u_n)_n$ in X. In other words, $E_{\infty }$ satisfies $(PS)_{c}$ condition for every $c<0$. The proof is complete. $\square$

6 Proof of Theorem 1

In this section we prove the main existence Theorem 1, whose statment is given in the Introduction, but, first, we recall briefly the definition of the genus inspired by [1]. Let Y be a real Banach space and let

$$\begin{aligned} \Sigma =\left\{ A\subset Y \backslash \left\{ 0\right\} | \,\ A \ \text {closed and symmetric}\ u\in A\Rightarrow -u\in A\right\} . \end{aligned}$$

Let $A\in \Sigma$, the genus $\gamma \left( A\right)$ of A is defined as the smallest integer N such that there exists $\Phi \in C\left( Y,{\mathbb {R}}^N\backslash \left\{ 0\right\} \right)$ such that $\Phi$ is odd and $\Phi \left( x\right) \ne 0$ for all $x\in A$. We set $\gamma \left( \emptyset \right) =0$ and $\gamma \left( A\right) =\infty$ if there are no integers with the above property.

The main properties of genus will be listed in the next proposition.

Proposition 1

Let $A,B\in \Sigma$, then

• a) If there exists $f\in C(A,Y)$ odd, then $\gamma (A)\le \gamma (f(A))$;

• b) If $A\subset B$ then $\gamma (A)\le \gamma (B)$;

• c) If there exists an odd homeomorphism between A and B, then $\gamma (A)=\gamma (B)$;

• d) If $S^{N-1}$ is the unit sphere in ${\mathbb {R}}^N$ then $\gamma (S^{N-1})=N$;

• e) $\gamma (A\cup B)\le \gamma (A)+\gamma (B)$;

• f) If $\gamma (B)<\infty$ then $\gamma (\overline{A{\setminus } B})\ge \gamma (A)-\gamma (B)$;

• g) If A is compact then $\gamma (A)<\infty$ and there exists a $\delta >0$ such that $\gamma (A)=\gamma (N_{\delta }(A))$, where $N_{\delta }(A)=\left\{ x\in Y: d(x,A)\le \delta \right\}$;

• h) If W is a subspace of X with codimension k and $\gamma (A)>k$ then $A\cap W\ne \emptyset$.

Remark 3

In particular, as emphasized by Struwe in Observation 5.5 in [40], if $A\in \Sigma$ is a finite collection of antipodal pairs $u_i$ and $-u_i$, then $\gamma (A)=1$.

For completeness, we recall the classical Deformation Lemma (see [39]).

Lemma 10

Let Y be a Banach space and consider $f\in C^{1}(Y,{\mathbb {R}})$ satisfying the (PS) condition. If $c\in {\mathbb {R}}$ and N is any neighborhood of

$$\begin{aligned} K_{c,f}:=\left\{ u\in Y: f(u)=c, f'(u)=0\right\} , \end{aligned}$$

then there exist $\eta (t,u)=\eta _{t}(u)\in C(\left[ 0,1\right] \times Y,Y)$ and constants ${\overline{\varepsilon }}>\varepsilon >0$ such that

• (1) $\eta _{0}(u)=u$ for all $u\in Y$;

• (2) $\eta _{t}(u)=u$ for all $u\notin f^{-1}\left[ c-{\overline{\varepsilon }}, c+{\overline{\varepsilon }}\right]$;

• (3) $\eta _{t}(u)=u$ is a homeomorphism of Y onto Y, for all $t\in [0,1]$;

• (4) $f(\eta _{t}(u))\le f(u)$ for all $t\in [0,1]$ and for all $u\in Y$;

• (5) $\eta _{1}(f^{c+\varepsilon }\backslash N)\subset f^{c-\varepsilon }$, where $f^{c}=\left\{ u\in Y: f(u)\le c\right\}$, for all $c\in {\mathbb {R}}$;

• (6) if $K_{c}=\emptyset$, $\eta _{1}(f^{c+\varepsilon })\subset f^{c-\varepsilon }$;

• (7) if f is even, $\eta _{t}$ is odd in u.

Note that, following Remark 3.5 in [40], it is enough to assume that (PS) condition holds at level c. Now, we are ready to prove our main result, that is the existence Theorem 1, whose statement is given in the Introduction.

Proof of Theorem 1.

Proof

Let $K_c=K_{c, E_{\infty }}=\left\{ u\in X:\, E_{\infty }(u)=c, \,\,E'_{\infty }(u)=0\right\} \,$ and take $m\in {\mathbb {N}}^+$. For $1\le j\le m$ define

$$\begin{aligned} c_{j}=\inf _{A\in \Sigma _{j}}\sup _{u\in A}E_{\infty }(u) \end{aligned}$$

where

$$\begin{aligned} \Sigma _{j}=\left\{ A\subset X\backslash \left\{ 0\right\} : A \ \text {is closed in} \ X,\,\, -A=A,\,\,\gamma (A)\ge j\right\} . \end{aligned}$$

We claim that

$$\begin{aligned} -\infty<c_j<0\quad \text {for all } j\ge 1. \end{aligned}$$

(65)

To reach the claim it is enough to prove that for all $j\in {\mathbb {N}}$, there is an $\varepsilon _{j}=\varepsilon (j)>0$ such that

$$\begin{aligned} \gamma (E_{\infty }^{-\varepsilon _{j}})\ge j, \,\ \text {where} \,\ E_{\infty }^{a}=\left\{ u\in X:\, E_{\infty }(u)\le a\right\} \quad \text {with} \quad a\in {\mathbb {R}}. \end{aligned}$$

(66)

Let $\Omega \subset {\mathbb {R}}^N$, $|\Omega |>0$, be a bounded open set in which $V>0$, eventually $\Omega \subset \Omega _V$ where $\Omega _V$ is given in the hypothesis. Extending functions u in $D^{1,p}_{0}(\Omega )$ by 0 outside $\Omega$, where $D_{0}^{1,p}(\Omega )$ is the closure of $C^{\infty }_{0}(\Omega )$ in the norm $\Vert u\Vert _{D^{1,p}_{0}(\Omega )} =\Vert D u\Vert _{L^p(\Omega )}$, then $u\in D^{1,p}({\mathbb {R}}^N)$ and we can assume that $D^{1,p}_{0}(\Omega )\subset X$. Let $W_{j}$ be a j-dimensional subspace of $D^{1,p}_{0}(\Omega )$. For every $v\in W_{j}$ with $\Vert v\Vert _{D^{1,p}_{0}(\Omega )}=1$, from the assumptions of V it is easy to see that there exists a $d_{j}>0$ such that

$$\begin{aligned} \int _{\Omega }V|v|^{k}dx\ge d_{j}. \end{aligned}$$

(67)

Since $W_{j}$ is a finite-dimensional space, all the norms in $W_{j}$ are equivalent. Thus, we can define

$$\begin{aligned} \begin{aligned}&a_{j}=\sup \left\{ \Vert D v\Vert _{q}^{q}: v\in W_{j}, \Vert v\Vert _{D^{1,p}_{0}(\Omega )}=1 \right\}<\infty ,\\&b_{j}=\sup \left\{ \Vert v\Vert _{p^{*}}^{p^{*}}: v\in W_{j}, \Vert v\Vert _{D^{1,p}_{0}(\Omega )}=1 \right\} <\infty . \end{aligned} \end{aligned}$$

(68)

On the other hand, for $t\in (0,T_{0})$, by (64) and since $K(x)\ge 0$ in ${\mathbb {R}}^N$, we arrive to

$$\begin{aligned} E_{\infty }(tv)=E_{\lambda }(tv)=\frac{1}{p}t^{p}+\frac{t^{q}}{q}\Vert D v\Vert _{q}^{q}-\frac{\lambda t^{k}}{k} \int _{\Omega }V|v|^{k}dx-\frac{t^{p^{*}}}{p^{*}}\int _{\Omega }K|v|^{p^{*}}dx, \end{aligned}$$

for every $v\in W_{j}$ with $\Vert v\Vert _{D^{1,p}_{0}(\Omega )}=1$. Now we obtain, thanks to (67) and (68),

$$\begin{aligned} E_{\infty }(tv)\le t^{q}\left( \frac{a_{j}}{q}-\frac{\lambda d_{j}}{k}t^{k-q} +\frac{1}{p} t^{p-q}\right) ,\quad t\in (0,T_0). \end{aligned}$$

Fig. 3

$\eta (t)$

Let

$$\begin{aligned} \eta (t)=c_3 -\lambda \frac{c_4}{k-q}t^{k-q}+\frac{c_5}{p-q}t^{p-q}, \end{aligned}$$

with positive constants given by $c_3={a_{j}}/q$, $c_4=d_{j}(k-q)/k$ and $c_5=(p-q)/p$, cfr. Fig. 3.

We prove first that there exists $T^{*}>0$ such that for all $\lambda >0$

$$\begin{aligned} \eta '(T^*)=0, \quad \eta (t)\ge \eta (T^*) \quad \text {in}\quad (0,T^*). \end{aligned}$$

(69)

First, we observe that $\eta (0)=c_3>0$, $\eta (t)\rightarrow \infty$ when $t\rightarrow \infty$ and $\eta '(t)<0$ when $t\rightarrow 0^{+}$, since $\eta '(t)=t^{k-q-1}\bigl (-\lambda c_4+c_5 t^{p-k}\bigr )$ and $p>k$. Moreover, from $\eta '(t)/t^{k-q-1}$ is strictly increasing, we deduce that there exists a unique $T^{*}>0$ such that $\eta '(T^*)=0$, with $T^{*}$ minimum for $\eta$, precisely $T^{*}=(\lambda c_4/c_5)^{1/(p-k)}$ and

$$\begin{aligned} \eta (T^*)=c_3 -\lambda ^{(p-q)/(p-k)} \Biggl ( \frac{c_4^{p-q}}{c_5^{k-q}}\Biggr )^{1/(p-k)} \frac{p-k}{(k-q)(p-q)}. \end{aligned}$$

In particular, $\eta (T^{*})<0$ if and only if $\lambda >\lambda _*$, where

$$\begin{aligned} \begin{aligned} \lambda _*&=\frac{c_5^{(k-q)/(p-q)}}{c_4}\Biggl (\frac{c_3(k-q)(p-q)}{p-k}\Biggr )^{(p-k)/(p-q)} \\&=\left( \frac{a_{j}}{q(p-k)}\right) ^{(p-k)/(p-q)}{p}^{(q-k)/(p-q)} \frac{k(p-q)}{d_{j}(k-q)^{(k-q)/(p-q)}}. \end{aligned} \end{aligned}$$

It holds $\lambda _*<\lambda ^*$, with $\lambda ^*$ defined in (62), if

$$\begin{aligned} \begin{aligned} \Vert K\Vert _\infty <&p^*\left( \frac{S}{p^*-k}\right) ^{(p^*-k)/(p-k)}\left( \frac{q}{a_{j}}\right) ^{(p^*-p)/(p-q)} \left( \frac{d_j(p^*-p)}{(p-q)\Vert V\Vert _r}\right) ^{(p^*-p)/(p-k)}\\&\quad \cdot (k-q)^{(k-q)(p^*-p)/(p-q)(p-k)}\left( 1-\frac{k}{p}\right) ^{(p^*-q)/(p-q)}, \end{aligned} \end{aligned}$$

(70)

say for $\Vert K\Vert _\infty$ sufficiently small.

Finally, we prove that $T^*\in (0,T_0)$ if $\lambda <\lambda ^*$. From $h(t)\le E_\lambda (tv)\le t^q\eta (t)$ for all $t>0$ and $v\in W_j$ with $\Vert v\Vert _{D^{1,p}_0}=1$, we deduce $h(T^*)<0$ so that $T^*\in (0,T_0)$ or $T^*>T_1$. Assume by contradiction that $T^*>T_1$, then $T^*>T$ or equivalently, using the explicit values of $T^*$ and T,

$$\begin{aligned} \lambda > \biggl [S^{p^*/p}\frac{p^*(p-k)}{\Vert K\Vert _\infty p(p^*-k)}\biggr ]^{(p-k)/(p^*-p)}\frac{k(p-q)}{d_j(k-q)p}. \end{aligned}$$

Since $\lambda <\lambda ^*$, then

$$\begin{aligned} S^{-k/p}\frac{\Vert V\Vert _r}{d_j}< \frac{k-q}{p-q}\cdot \frac{p^*-p}{p^*-k}<1, \end{aligned}$$

(71)

but, by (67), we have $d_j \le \Vert V\Vert _r \Vert v\Vert _{p^*}^k\le S^{-k/p}\Vert V\Vert _r$ being $\Vert v\Vert _{D^{1,p}_0}=1$, so that (71) produces the required contradiction since $S^{-k/p}{\Vert V\Vert _r}/{d_j}\ge 1$. Consequently, $T^*\in (0,T_0)$.

Thus, (69) is verified for $T^*\in (0,T_0)$ and with $\eta (T^*)<0$ if $\lambda \in (\lambda _{*},\lambda ^{*})$, consequently

$$\begin{aligned} E_{\infty }(T^* v)\le -\varepsilon _j<0,\qquad \varepsilon _j=-(T^*)^q\eta (T^*). \end{aligned}$$

Denote $S_{T^*}=\left\{ v \in X: \Vert v\Vert _{D^{1,p}_{0}(\Omega )}=T^*\right\} ,$ then $S_{T^*}\cap W_{j}\subset E_{\infty }^{-\varepsilon _{j}}$. By Proposition 1,

$$\begin{aligned} \gamma (E_{\infty }^{-\varepsilon _{j}})\ge \gamma (S_{T^*}\cap W_{j})=j, \end{aligned}$$

which proves (66). Consequently, $E_{\infty }^{-\varepsilon _{j}}\in \Sigma _{j}$, in turn

$$\begin{aligned} c_j\le \sup _{u\in E_{\infty }^{-\varepsilon _{j}}}E_{\infty }(u)\le -\varepsilon _{j}<0. \end{aligned}$$

Furthermore, $E_{\infty }$ is bounded from below, hence $c_{j}>-\infty$ (that is why we consider $E_{\infty }$ instead of $E_{\lambda }$), thus the proof of claim (65) is concluded.

By [11] and [39], it follows from (65) that $c_j$, $j\in {\mathbb {N}}$, is a critical value for $E_\infty$. Then, from Lemma 9, we see that $E_{\infty }$ satisfies the $(PS)_{c_j}$ condition for all $c_j<0$ and this implies that $K_{c_j}$ is a compact set, hence $\gamma (K_{c_j})<\infty$ by virtue of Proposition 1.

We claim that, if for some $j\in {\mathbb {N}}$ there is an $i\ge 1$ such that if

$$\begin{aligned} c=c_{j}=c_{j+1}=\dots =c_{j+i},\quad \text {then}\quad \gamma (K_{c})\ge i+1. \end{aligned}$$

(72)

In particular, as a consequence of Remark 3 (cfr. Lemma 5.6 Chapter II in [40]), if $\gamma (K_{c})>1$ then $K_{c}$ is infinite.

The proof is almost standard, but for completeness we enclose it. We proceed by contradiction. If $\gamma (K_{c})\le i$, there exists a closed and symmetric set U with $K_{c}\subset U$ and $\gamma (U)\le i$, since $c<0$, we can also assume that the closed set $U\subset E_{\infty }^{0}$. Using Lemma 10-(5), there is an odd homeomorphism $\eta :[0,1]\times X\rightarrow X$ such that $\eta _1(E_{\infty }^{c+\delta }\backslash U)\subset E_{\infty }^{c-\delta }$ for some $\delta \in (0,-c)$. From definition of $c=c_{j+i}$, there exists an $A\in \Sigma _{j+i}$ for which $\sup _{u\in A} E_{\infty }(u)<c+\delta$. Thus, from Proposition 10, (2) and (5) respectively,

$$\begin{aligned} \eta _1(A\backslash U)\subset \eta _1(E_{\infty }^{c+\delta }\backslash U)\subset E_{\infty }^{c-\delta }, \end{aligned}$$

which means

$$\begin{aligned} \sup _{u\in \eta _1(A\backslash U)} E_{\infty }(u)\le c-\delta . \end{aligned}$$

(73)

But Proposition 1-(a),(b) and (f) being $\gamma (U)<\infty$ and since $A{\setminus } U$ is closed, reveals that

$$\begin{aligned} \gamma (\overline{\eta _1(A\backslash U) })\ge \gamma (\eta _1(A\backslash U) )\ge \gamma ({A\backslash U}) =\gamma (\overline{A\backslash U})\ge \gamma (A)-\gamma (U)\ge j. \end{aligned}$$

Hence $\overline{\eta _1(A\backslash U)}\in \Sigma _{j}$, so that by definition of $c_j$ and thanks to (73),

$$\begin{aligned} c=c_{j}\le \sup _{u \in \overline{\eta _1(A\backslash U)}} E_{\infty }(u)=\sup _{u \in \eta _1(A\backslash U)} E_{\infty }(u) \le c-\delta . \end{aligned}$$

This contradiction proves claim (72).

To complete the proof, we observe that for all $j\in {\mathbb {N}}^+$, we have

$$\begin{aligned} \Sigma _{j+1}\subset \Sigma _{j}\quad \text {and}\quad c_{j}\le c_{j+1}<0. \end{aligned}$$

If all $c_{j}$ are distinct, then $\gamma (K_{c_{j}})\ge 1$, so that $K_{c_{j}}\ne \emptyset$ and thus $(c_{j})_j$ is a sequence of distinct negative critical values of $E_{\infty }$, thus a sequence of solutions with negative energy is obtained, as required.

If for some $j_{0}$, there exists an $i\ge 1$ such that

$$\begin{aligned} c=c_{j_{0}}=c_{j_{0}+1}=\dots =c_{j_{0}+i}, \end{aligned}$$

from (72) we have $\gamma (K_{c_{j_{0}}})\ge i+1>1$, which shows that $K_{c_{j_{0}}}$ has infinitely many distinct elements. Also in this case we arrive to a sequence of solutions with negative energy.

By Lemma 9, then $E_{\lambda }(u)=E_{\infty }(u)$ when $E_{\infty }(u)<0$, so that the functional $E_{\lambda }(u)$, being even, possesses at least m pairs of critical nonzero points of with negative critical values. Therefore, problem $({\mathcal {P}})$ has at least 2m weak nontrivial solutions with negative energy. $\square$