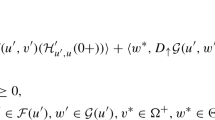Skip to main content
SpringerLink
Log in

The p-capacitary Orlicz–Hadamard variational formula and Orlicz–Minkowski problems

  • Published:
Calculus of Variations and Partial Differential Equations Aims and scope Submit manuscript

Abstract

In this paper, combining the p-capacity for \(p\in (1, n)\) with the Orlicz addition of convex domains, we develop the p-capacitary Orlicz–Brunn–Minkowski theory. In particular, the Orlicz \(L_{\phi }\) mixed p-capacity of two convex domains is introduced and its geometric interpretation is obtained by the p-capacitary Orlicz–Hadamard variational formula. The p-capacitary Orlicz–Brunn–Minkowski and Orlicz–Minkowski inequalities are established, and the equivalence of these two inequalities are discussed as well. The p-capacitary Orlicz–Minkowski problem is proposed and solved under some mild conditions on the involving functions and measures. In particular, we provide the solutions for the normalized p-capacitary \(L_q\) Minkowski problems with \(q>1\) for both discrete and general measures.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Akman, M., Gong, J., Hineman, J., Lewis, J., Vogel, A.: The Brunn–Minkowski inequality and a Minkowski problem for nonlinear capacity, preprint. arXiv:1709.00447

  2. Aleksandrov, A.: On the theory of mixed volume. III. Extension of two theorems of Minkowski on convex polyhedra to arbitrary convex bodies. Mat. Sb. (N.S.) 2, 27–46 (1938) (in Russian)

  3. Borell, C.: Capacitary inequalities of the Brunn–Minkowski type. Math. Ann. 263, 179–184 (1983)

    Article  MathSciNet  MATH  Google Scholar 

  4. Böröczky, K.: Stronger versions of the Orlicz–Petty projection inequality. J. Differ. Geom. 95, 215–247 (2013)

    Article  MathSciNet  MATH  Google Scholar 

  5. Böröczky, K., Hegedus, P., Zhu, G.: On the discrete logarithmic Minkowski problem. Int. Math. Res. Not. 2016, 1807–1838 (2016)

    Article  MathSciNet  MATH  Google Scholar 

  6. Böröczky, K., Lutwak, E., Yang, D., Zhang, G.: The log-Brunn–Minkowski inequality. Adv. Math. 231, 1974–1997 (2012)

    Article  MathSciNet  MATH  Google Scholar 

  7. Böröczky, K., Lutwak, E., Yang, D., Zhang, G.: The logarithmic Minkowski problem. J. Am. Math. Soc. 26, 831–852 (2013)

    Article  MathSciNet  MATH  Google Scholar 

  8. Caffarelli, L., Jerison, D., Lieb, E.: On the case of equality in the Brunn–Minkowski inequality for capacity. Adv. Math. 117, 193–207 (1996)

    Article  MathSciNet  MATH  Google Scholar 

  9. Chen, W.: \(L_p\) Minkowski problem with not necessarily positive data. Adv. Math. 201, 77–89 (2006)

    Article  MathSciNet  MATH  Google Scholar 

  10. Chou, K., Wang, X.: The \(L_p\) Minkowski problem and the Minkowski problem in centroaffine geometry. Adv. Math. 205, 33–83 (2006)

    Article  MathSciNet  MATH  Google Scholar 

  11. Colesanti, A., Salani, P.: The Brunn–Minkowski inequality for \(p\)-capacity of convex bodies. Math. Ann. 327, 459–479 (2003)

    Article  MathSciNet  MATH  Google Scholar 

  12. Colesanti, A., Nyström, K., Salani, P., Xiao, J., Yang, D., Zhang, G.: The Hadamard variational formula and the Minkowski problem for \(p\)-capacity. Adv. Math. 285, 1511–1588 (2015)

    Article  MathSciNet  MATH  Google Scholar 

  13. Evans, E., Gariepy, R.: Measure Theory and Fine Properties of Functions. CRC Press, Boca Raton (1992)

    MATH  Google Scholar 

  14. Gardner, R.: The Brunn–Minkowski inequality. Bull. Am. Math. Soc. 39, 355–405 (2002)

    Article  MathSciNet  MATH  Google Scholar 

  15. Gardner, R., Hug, D., Weil, W.: Operations between sets in geometry. J. Eur. Math. Soc. 15, 2297–2352 (2013)

    Article  MathSciNet  MATH  Google Scholar 

  16. Gardner, R., Hug, D., Weil, W.: The Orlicz–Brunn–Minkowski theory: a general framework, additions, and inequalities. J. Differ. Geom. 97, 427–476 (2014)

    Article  MathSciNet  MATH  Google Scholar 

  17. Gardner, R., Hug, D., Weil, W., Ye, D.: The dual Orlicz–Brunn–Minkowski theory. J. Math. Anal. Appl. 430, 810–829 (2015)

    Article  MathSciNet  MATH  Google Scholar 

  18. Haberl, C., Lutwak, E., Yang, D., Zhang, G.: The even Orlicz Minkowski problem. Adv. Math. 224, 2485–2510 (2010)

    Article  MathSciNet  MATH  Google Scholar 

  19. Haberl, C., Parapatits, L.: The centro-affine Hadwiger theorem. J. Am. Math. Soc. 27, 685–705 (2014)

    Article  MathSciNet  MATH  Google Scholar 

  20. Hou, S., Ye, D.: Orlicz addition for measures and an optimization problem for the \(f\)-divergence, preprint. arXiv:1606.02155

  21. Hu, C., Ma, X., Shen, C.: On the Christoffel–Minkowski problem of Firey’s \(p\)-sum. Calc. Var. Partial Differ. Equ. 21, 137–155 (2004)

    Article  MathSciNet  MATH  Google Scholar 

  22. Huang, Q., He, B.: On the Orlicz Minkowski problem for polytopes. Discrete Comput. Geom. 48, 281–297 (2012)

    Article  MathSciNet  MATH  Google Scholar 

  23. Hug, D., Lutwak, E., Yang, D., Zhang, G.: On the \(L_p\) Minkowski problem for polytope. Discrete Comput. Geom. 33, 699–715 (2005)

    Article  MathSciNet  MATH  Google Scholar 

  24. Jerison, D.: A Minkowski problem for electrostatic capacity. Acta Math. 176, 1–47 (1996)

    Article  MathSciNet  MATH  Google Scholar 

  25. Jerison, D.: The direct method in the calculus of variations for convex bodies. Adv. Math. 122, 262–279 (1996)

    Article  MathSciNet  MATH  Google Scholar 

  26. Lewis, J.: Capacitary functions in convex rings. Arch. Ration. Mech. Anal. 66, 201–224 (1977)

    Article  MathSciNet  MATH  Google Scholar 

  27. Lewis, J., Nyström, K.: Boundary behaviour for \(p\)-harmonic functions in Lipschitz and starlike Lipschitz ring domains. Ann. Sci. Éc. Norm. Supér. 40, 765–813 (2007)

    Article  MathSciNet  MATH  Google Scholar 

  28. Lewis, J., Nyström, K.: Regularity and free boundary regularity for the \(p\)-Laplacian in Lipschitz and \(C^1\)-domains. Ann. Acad. Sci. Fenn. Math. 33, 523–548 (2008)

    MathSciNet  MATH  Google Scholar 

  29. Ludwig, M.: General affine surface areas. Adv. Math. 224, 2346–2360 (2010)

    Article  MathSciNet  MATH  Google Scholar 

  30. Lutwak, E.: The Brunn–Minkowski–Firey theory I: mixed volumes and the Minkowski problem. J. Differ. Geom. 38, 131–150 (1993)

    Article  MathSciNet  MATH  Google Scholar 

  31. Lutwak, E., Yang, D., Zhang, G.: On the \(L_p\)-Minkowski problem. Trans. Am. Math. Soc. 356, 4359–4370 (2004)

    Article  MathSciNet  MATH  Google Scholar 

  32. Lutwak, E., Yang, D., Zhang, G.: Orlicz projection bodies. Adv. Math. 223, 220–242 (2010)

    Article  MathSciNet  MATH  Google Scholar 

  33. Lutwak, E., Yang, D., Zhang, G.: Orlicz centroid bodies. J. Differ. Geom. 84, 365–387 (2010)

    Article  MathSciNet  MATH  Google Scholar 

  34. Protasov, V.: On possible generalizations of convex addition. Vestnik Moskov. Univ. Ser. I Mat. Mekh. 71, 13–18 (in Russian); translation in Moscow Univ. Math. Bull. 54(1999), 12–17 (1999)

  35. Protasov, V.: A generalized joint spectral radius. A geometric approach. Izv. Ross. Akad. Nauk Ser. Mat. 61, 99–136 (in Russian); translation in Izv. Math. 61(1997), 995–1030 (1997)

  36. Schneider, R.: Convex Bodies: The Brunn–Minkowski Theory, 2nd expanded edn. Cambridge University Press, Cambridge (2014)

    Google Scholar 

  37. Stancu, A.: The discrete planar \(L_0\)-Minkowski problem. Adv. Math. 167, 160–174 (2002)

    Article  MathSciNet  MATH  Google Scholar 

  38. Stancu, A.: On the number of solutions to the discrete two-dimensional \(L_0\)-Minkowski problem. Adv. Math. 180, 290–323 (2003)

    Article  MathSciNet  MATH  Google Scholar 

  39. Stancu, A.: The necessary condition for the discrete \(L_0\)-Minkowski problem in \(\mathbb{R}^2\). J. Geom. 88, 162–168 (2008)

    Article  MathSciNet  MATH  Google Scholar 

  40. Umanskiy, V.: On solvability of two-dimensional \(L_p\)-Minkowski problem. Adv. Math. 180, 176–186 (2003)

    Article  MathSciNet  MATH  Google Scholar 

  41. Xi, D., Leng, G.: Dar’s conjecture and the log-Brunn–Minkowski inequality. J. Differ. Geom. 103, 145–189 (2016)

    Article  MathSciNet  MATH  Google Scholar 

  42. Xi, D., Jin, H., Leng, G.: The Orlicz Brunn–Minkowski inequality. Adv. Math. 260, 350–374 (2014)

    Article  MathSciNet  MATH  Google Scholar 

  43. Ye, D.: Inequalities for general mixed affine surface areas. J. Lond. Math. Soc. 85, 101–120 (2012)

    Article  MathSciNet  MATH  Google Scholar 

  44. Ye, D.: On the monotone properties of general affine surfaces under the Steiner symmetrization. Indiana Univ. Math. J. 14, 1–19 (2014)

    Article  MathSciNet  MATH  Google Scholar 

  45. Ye, D.: New Orlicz affine isoperimetric inequalities. J. Math. Anal. Appl. 427, 905–929 (2015)

    Article  MathSciNet  MATH  Google Scholar 

  46. Ye, D.: Dual Orlicz–Brunn–Minkowski theory: dual Orlicz \(L_{\phi }\) affine and geominimal surface areas. J. Math. Anal. Appl. 443, 352–371 (2016)

    Article  MathSciNet  MATH  Google Scholar 

  47. Zhu, B., Hong, H., Ye, D.: The Orlicz–Petty bodies. Int. Math. Res. Not. arXiv:1611.04436 (in press)

  48. Zhu, G.: The logarithmic Minkowski problem for polytopes. Adv. Math. 262, 909–931 (2014)

    Article  MathSciNet  MATH  Google Scholar 

  49. Zhu, G.: The \(L_p\) Minkowski problem for polytopes for \(0 < p < 1\). J. Funct. Anal. 269, 1070–1094 (2015)

    Article  MathSciNet  MATH  Google Scholar 

  50. Zhu, G.: The centro-affine Minkowski problem for polytopes. J. Differ. Geom. 101, 159–174 (2015)

    Article  MathSciNet  MATH  Google Scholar 

  51. Zhu, G.: The \(L_p\) Minkowski problem for polytopes for \(p < 0\). Indiana Univ. Math. J. 66, 1333–1350 (2017)

    Article  MathSciNet  MATH  Google Scholar 

  52. Zou, D., Xiong, G.: Orlicz–John ellipsoids. Adv. Math. 265, 132–168 (2014)

    Article  MathSciNet  MATH  Google Scholar 

  53. Zou, D., Xiong, G.: A unified treatment for \(L_p\) Brunn–Minkowski type inequalities. Commun. Anal. Geom. arXiv:1607.07141 (in press)

Download references

Acknowledgements

Deping Ye is supported by a NSERC grant. The authors are greatly indebted to Dr. J. Xiao for his valuable discussions and to the referee for many valuable comments which improve largely the quality of the paper.

Author information

Authors and Affiliations

  1. Department of Mathematics and Statistics, Memorial University of Newfoundland, St. John’s, NL, A1C 5S7, Canada

    Han Hong & Deping Ye

  2. Department of Mathematical and Statistical Sciences, University of Alberta, Edmonton, AB, T6G 2G1, Canada

    Ning Zhang

Authors
  1. Han Hong
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Deping Ye
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Ning Zhang
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Ning Zhang.

Additional information

Communicated by L. Caffarelli.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Hong, H., Ye, D. & Zhang, N. The p-capacitary Orlicz–Hadamard variational formula and Orlicz–Minkowski problems. Calc. Var. 57, 5 (2018). https://doi.org/10.1007/s00526-017-1278-6

Download citation

  • Received:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s00526-017-1278-6

Mathematics Subject Classification

Search

Navigation