Abstract
Given a smooth manifold M and a totally nonholonomic distribution \(\Delta \subset TM \) of rank \(d\ge 3\), we study the effect of singular curves on the topology of the space of horizontal paths joining two points on M. Singular curves are critical points of the endpoint map \(F\,{:}\,\gamma \mapsto \gamma (1)\) defined on the space \(\Omega \) of horizontal paths starting at a fixed point x. We consider a sub-Riemannian energy \(J\,{:}\,\Omega (y)\rightarrow \mathbb R\), where \(\Omega (y)=F^{-1}(y)\) is the space of horizontal paths connecting x with y, and study those singular paths that do not influence the homotopy type of the Lebesgue sets \(\{\gamma \in \Omega (y)\,|\,J(\gamma )\le E\}\). We call them homotopically invisible. It turns out that for \(d\ge 3\) generic sub-Riemannian structures in the sense of Chitour et al. (J Differ Geom 73(1):45–73, 2006) have only homotopically invisible singular curves. Our results can be seen as a first step for developing the calculus of variations on the singular space of horizontal curves (in this direction we prove a sub-Riemannian minimax principle and discuss some applications).


Similar content being viewed by others
Notes
This definition requires the choice of an inner product in each fiber (a sub-Riemannian structure on \(\Delta \)) in order to integrate the square of the norm of \(\dot{\gamma }\), but the fact of being integrable is independent of the chosen structure (we refer the reader to [2, 14, 15] for more details).
Note that, when \(\Omega (y)\) is singular it is not clear yet what a “critical point” for J should be; this will be clarified below.
We recall that \(\overrightarrow{H}\) is defined by the equation \(\iota _{\overrightarrow{H}}\omega =-dH\)
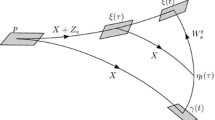
Here we chose \(\tilde{r} \) such that \(2\tilde{r}\subset W_1\) in order to guarantee that:
$$\begin{aligned} \text {clos}\left( (\phi ^u)^{-1}(U_3\times 2\tilde{r}ac/3B)\right) \subset \text {clos}\left( U_3\times \tilde{r} B\right) . \end{aligned}$$(7)We will need this property in the proof of Corollary 8.
This follows from this elementary fact. Let \(F\,{:}\,P\times K\rightarrow \mathbb {R}\) be a continuous function, where P and K are (just) topological spaces and K is compact. Define \(f(p)=\max _{k\in K}F(p,k)\). Then f is continuous (and the analogue statement with \(\max \) replaced with \(\min \) is also true). The proof is easy and left to the reader.
References
Agrachev, A.A., Boscain, U., Barilari, D.: Introduction to Riemannian and sub-Riemannian geometry, lectures notes version. https://webusers.imj-prg.fr/~davide.barilari/ABB-SRnotes-110715.pdf. Accessed 11 July 2015
Agrachev, A.A., Boscain, U., Barilari, D.: In geometry, analysis and dynamics on sub-Riemannian manifolds, vol. II, EMS, October 2016 (2016)
Agrachev, A.A., Sachkov, Y.L.: Control Theory from the Geometric Viewpoint, vol. 87. Springer, Berlin (2013)
Boarotto, F., Lerario, A.: Homotopy properties of horizontal loop spaces and a theorem of Serre in sub-Riemannian geometry. http://arxiv.org/pdf/1502.07452.pdf
Chang, K.: Infinite Dimensional Morse Theory and Multiple Solution Problems. Birkhäuser, Boston (1993)
Chitour, Y., Jean, F., Trélat, E.: Genericity results for singular curves. J. Differ. Geom. 73(1), 45–73 (2006)
Chitour, Y., Jean, F., Trélat, E.: Singular trajectories of control-affine systems. SIAM J. Control Optim. 47(2), 1078–1095 (2008)
Clarke, F.H.: On the inverse function theorem. Pac. J. Math. 64(1), 97–102 (1976)
Clarke, F.H.: Optimization and Nonsmooth Analysis, Canadian Mathematical Society Series of Monographs and Advanced Texts. Wiley, New York (1983)
Lerario, A., Mondino, A.: Homotopy properties of horizontal loop-spaces and applications to closed sub-Riemannian geodesics. http://arxiv.org/pdf/1509.07000v1
Dominy, J., Rabitz, H.: Dynamic homotopy and landscape dynamical set topology in quantum control. J. Math. Phys. 53, 082201 (2012). doi:10.1063/1.4742375
Hatcher, A.: Algebraic Topology. Cambridge University Press, Cambridge (2002)
Hurewicz, W.: On the concept of fiber space. Proc. Natl. Acad. Sci. USA 41(11), 956–961 (1955)
Montgomery, R.: A tour of sub-Riemannian geometries, their geodesics and applications. AMS Mathematical Surveys and Monographs No. 91 (2006)
Rifford, L.: Sub-Riemannian geometry and optimal transport. Springer Briefs in Mathematics. Springer, Cham (2014)
Sarychev, A.V.: On homotopy properties of the space of trajectories of a completely nonholonomic differential system. Sov. Math. Dokl. 42, 674–678 (1991)
Serre, J.P.: Homologie singuliere Des espaces fibres. Ann. Math. Second Ser. 54(3), 425–505 (1951)
Smale, S.: Regular curves on Riemannian manifolds. Trans. Am. Math. Soc. 87, 492–512 (1958)
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by A. Malchiodi.
Rights and permissions
About this article
Cite this article
Agrachev, A.A., Boarotto, F. & Lerario, A. Homotopically invisible singular curves. Calc. Var. 56, 105 (2017). https://doi.org/10.1007/s00526-017-1203-z
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s00526-017-1203-z