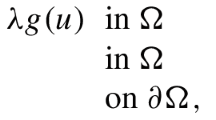Abstract
We prove the existence of solutions of a class of quasilinear elliptic problems with Dirichlet boundary conditions of the following form
where \(\Omega \subset \mathbb R^N\) is a bounded domain, \(N\ge 2\), the differential operator is \(Lu= -\hbox {div}( |\nabla u|^{p-2}\nabla u )-\lambda _1 |u|^{p-2}u\) with \(X=W^{1,p}_0(\Omega )\) or \(Lu= \Delta ^2u -\lambda _1 u\) with \(X=H^2_0(\Omega )\), the nonlinearity is given by \(g(u)=(u^+ )^q\) or \(g(u)=|u|^{q-1}u\) i.e. it is a superlinear, at most critical, term and \(f\) is a small reaction term. We give an abstract formulation for which solutions are found by minimization on an appropriate subset of the Nehari manifold associated to our problem. Our method can be also applied to other related problems involving indefinite weights.
Similar content being viewed by others
References
Badiale, M., Serra, E.: Semilinear Elliptic Equations for Beginners. Universitext. Springer, London (2011). Existence results via the variational approach
de Figueiredo, D.: Positive solutions of semilinear elliptic problems, differential equations. Lecture Notes in Mathematics, vol. 957, pp. 34–87. Springer, Berlin (1982)
Cuesta, M., De Coster, C.: A resonant-superlinear elliptic problem revisited. Adv. Nonl. Stud. 13, 97–114 (2013)
Cuesta, M., de Figueiredo, D., Srikanth, P.N.: On a resonant-superlinear elliptic problem. Calc. Var. Part. Differ. Equ. 17, 221–233 (2003)
de Figueiredo, D., Yang Jianfu: Critical superlinear Ambrosetti-Prodi problems. Top. Meth. Nonlin. Anal. 14, 59–80 (1999)
Drabek, P., Takac, P.: Poincaré inequality and Palais-Smale condition for the \(p\)-laplacian. Calc. Var. Part. Differ. Equ. 29, 31–58 (2007)
Fleckinger, J., Takac, P.: An improved Poincaré inequality and the \(p\)-laplacian at resonance for p> 2. Adv. Differ. Equ. 7, 951–971 (2002)
Kannan, R., Ortega, R.: Landesman-Lazer conditions for problems with “one-sided unbounded” nonlinearities. Nonl. Anal. T.M.A. 9 (1985), 1313–1317
Kannan, R., Ortega, R.: Superlinear elliptic boundary value problems. Czechoslovak Mathematical J. 37, 386–399 (1987)
Ortega, J.H., Zuazua, E.: Generic simplicity of the spectrum and stabilization for a plate equation. SIAM J. Cont. Optim. 39:1585–1614 + SIAM. J. Control. Optim. 42(2003), 1905–1910 (2001)
Tarantello, G.: On nonhomogeneous elliptic equations involving critical Sobolev exponent. Ann. I.H.P. Sect. C 9, 281–304 (1992)
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by A. Malchiodi.
Rights and permissions
About this article
Cite this article
Cuesta, M., De Coster, C. Superlinear critical resonant problems with small forcing term. Calc. Var. 54, 349–363 (2015). https://doi.org/10.1007/s00526-014-0788-8
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00526-014-0788-8