Skip to main content
SpringerLink
Log in

A MAS approach for vehicle routing problem

  • Original Article
  • Published:
Neural Computing and Applications Aims and scope Submit manuscript

Abstract

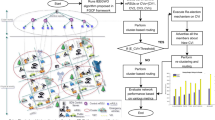
The Vehicle Routing Problem (VRP) is a class of well-known combinatorial optimization problems. The great interest in the VRP is due to its practical importance, as well as the difficulty in solving it. The Capacitated Vehicle Routing Problem (CVRP) is the most common variant of the VRP. Most of the approaches that have been developed to solve this problem tend to solve the problem in a centralized way. There has been very little research done into solving this problem in a distributed manner. In this paper, we propose an innovative approach for solving CVRP in a distributed manner based on multi-agent systems and using the game theory, which consists of three types of intelligent agents: customer agent, vehicle agent, and depot agent and includes the two phases: cluster construction and clusters optimization. The cluster construction phase consists of playing a Game Theoretic Clustering Algorithm by customer agents to divide the customers into several clusters, each consisting of a cluster head and several member customers. Then, we present a Game Theoretic Clusters Optimization Algorithm for the cluster optimization phase, which is played by vehicle agents to minimize the cost of each vehicle’s route to optimize the quality of the solution. The performance of the proposed approach is evaluated on 48 instances from 10 standard benchmark sets and compared with some state-of-the-art methods in terms of execution time and quality of solutions. Our experiments illustrated that the proposed method can compete or even outperform much more complex algorithms.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9

Similar content being viewed by others

References

  1. Ai TJ, Kachitvichyanukul V (2009) Particle swarm optimization and two solution representations for solving the capacitated vehicle routing problem. Comput Ind Eng 56(1):380–387

    Google Scholar 

  2. Akkarajitsakul K, Hossain E, Niyato D, Kim DI (2011) Game theoretic approaches for multiple access in wireless networks: a survey. IEEE Commun Surv Tut 13(3):372–395

    Google Scholar 

  3. Alba E, Dorronsoro B (2006) Computing nine new best-so-far solutions for capacitated VRP with a cellular genetic algorithm. Inf Process Lett 98(6):225–230

    MathSciNet  MATH  Google Scholar 

  4. Alipour MM, Razavi SN (2015) A new multiagent reinforcement learning algorithm to solve the symmetric traveling salesman problem. Multiagent Grid Syst 11(2):107–119

    Google Scholar 

  5. Alipour MM, Razavi SN (2019) A new local search heuristic based on nearest insertion into the convex hull for solving Euclidean TSP. Int J Oper Res 34(3):409–429

    MathSciNet  Google Scholar 

  6. Alipour MM, Razavi SN, Derakhshi MRF, Balafar MA (2018) A hybrid algorithm using a genetic algorithm and multiagent reinforcement learning heuristic to solve the traveling salesman problem. Neural Comput App 30(9):2935–2951

    Google Scholar 

  7. AlSkaif T, Zapata MG, Bellalta B (2015) Game theory for energy efficiency in wireless sensor networks: latest trends. J Netw Comput Appl 54:33–61

    Google Scholar 

  8. Amous M, Toumi S, Jarboui B, Eddaly M (2017) A variable neighborhood search algorithm for the capacitated vehicle routing problem. Elect Notes Disc Math 58:231–238

    MathSciNet  MATH  Google Scholar 

  9. Aragão DP, Novaes AG, Luna MMM (2015) A multi agent based system to enable dynamic vehicle routing. TRANSPORTES 23(1):69–77

    Google Scholar 

  10. Asawasakulsorn A (2015) Transportation collaboration: partner selection criteria and interorganizational system design issues for supporting trust. Int J Bus Inf, 4(2).

  11. Augerat P, Belenguer JM, Benavent E, Corberán A, Naddef D, Rinaldi G (1995) Computational results with a branch and cut code for the capacitated vehicle routing problem. IMAG.

  12. Baker BM, Ayechew M (2003) A genetic algorithm for the vehicle routing problem. Comput Oper Res 30(5):787–800

    MathSciNet  MATH  Google Scholar 

  13. Baldacci R, Toth P, Vigo D (2010) Exact algorithms for routing problems under vehicle capacity constraints. Ann Oper Res 175(1):213–245

    MathSciNet  MATH  Google Scholar 

  14. Barbucha D, Jedrzejowicz P (2008) Multi-agent platform for solving the dynamic vehicle routing problem. Paper presented at the Intelligent Transportation Systems, 2008. ITSC 2008. 11th International IEEE Conference on.

  15. Barbucha D, Jȩdrzejowicz P (2009) Agent-based approach to the dynamic vehicle routing problem. In: Demazeau Y, Pavón J, Corchado JM, Bajo J (eds) 7th International Conference on Practical Applications of Agents and Multi-Agent Systems (PAAMS 2009). Advances in Intelligent and Soft Computing, vol 55. Springer, Berlin, Heidelberg, 169–178.

  16. Bodin L, Golden B (1981) Classification in vehicle routing and scheduling. Networks 11(2):97–108

    Google Scholar 

  17. Bouzid MC, Haddadene HA, Salhi S (2017) An integration of Lagrangian split and VNS: The case of the capacitated vehicle routing problem. Comput Oper Res 78:513–525

    MathSciNet  MATH  Google Scholar 

  18. Bullnheimer B, Hartl RF, Strauss C (1999) Applying the ant system to the vehicle routing problem. In Meta-heuristics (pp. 285–296): Springer.

  19. Chan FT, Zhang T (2011) The impact of collaborative transportation management on supply chain performance: a simulation approach. Expert Syst Appl 38(3):2319–2329

    Google Scholar 

  20. Charilas DE, Panagopoulos AD (2010) A survey on game theory applications in wireless networks. Comput Netw 54(18):3421–3430

    MATH  Google Scholar 

  21. Chen A-L, Yang G-K, Wu Z-M (2006) Hybrid discrete particle swarm optimization algorithm for capacitated vehicle routing problem. J Zhejiang Univ Sci A 7(4):607–614

    MATH  Google Scholar 

  22. Christofides N, Eilon S (1969) An algorithm for the vehicle-dispatching problem. ORiON: The Journal of ORSSA, 309–318.

  23. Christofides N, Mingozzi A, Toth P (1979) The vehicle routing problem. In: Christofides N, Mingozzi A, Toth P, Sandi C (eds) Combinatorial optimization. Wiley, Chichester, pp 315–338

    MATH  Google Scholar 

  24. Clarke G, Wright JW (1964) Scheduling of vehicles from a central depot to a number of delivery points. Oper Res 12:568–581

    Google Scholar 

  25. Cornuéjols G, Harche F (1993) Polyhedral study of the capacitated vehicle routing problem. Math Program 60:21–52

    MathSciNet  MATH  Google Scholar 

  26. Dan Z, Cai L, Zheng L (2009) Improved multi-agent system for the vehicle routing problem with time windows. Tsinghua Sci Technol 14(3):407–412

    Google Scholar 

  27. Dantzig GB, Ramser JH (1959) The truck dispatching problem. Manage Sci 6(1):80–91

    MathSciNet  MATH  Google Scholar 

  28. Davidsson P, Henesey L, Ramstedt L, Törnquist J, Wernstedt F (2005) An analysis of agent-based approaches to transport logistics. Transp Res part C Emerg Technol 13(4):255–271

    MATH  Google Scholar 

  29. Dongarra JJ (2014) Performance of various computers using standard linear equations software. Retrieved from

  30. Engevall S, Gothe-Lundgren M, Varbrand P (2004) The heterogeneous vehicle-routing game. Transp Sci 38(1):71–85

    MATH  Google Scholar 

  31. Ergun Ö, Kuyzu G, Savelsbergh M (2007) Shipper collaboration. Comput Oper Res 34(6):1551–1560

    MATH  Google Scholar 

  32. Fernandes FC, de Souza SR, Silva MAL, Borges HE, Ribeiro FF (2009) A multiagent architecture for solving combinatorial optimization problems through metaheuristics. Paper presented at the Systems, Man and Cybernetics, 2009. SMC 2009. IEEE International Conference on.

  33. Fisher ML (1994) Optimal solution of vehicle routing problems using minimum k-trees. Oper Res 42(4):626–642

    MathSciNet  MATH  Google Scholar 

  34. Fisher RA (1921) On the probable error of a coefficient of correlation deduced from a small sample. Metron 1:3–32

    Google Scholar 

  35. Fudenberg D, Tirole J (1991) Game theory. In: MIT press Cambridge, MA.

  36. Gaskell T (1967) Bases for vehicle fleet scheduling. J Oper Res Soc 18(3):281–295

    Google Scholar 

  37. Gendreau M, Potvin JY, Bräumlaysy O, Hasle G, Løkketangen A (2008) Metaheuristics for the vehicle routing problem and its extensions: A categorized bibliography. In The vehicle routing problem: latest advances and new challenges (pp. 143–169): Springer

  38. Gillett BE, Miller LR (1974) A heuristic algorithm for the vehicle-dispatch problem. Oper Res 21:340–349

    MATH  Google Scholar 

  39. Golden BL, Wasil EA, Kelly JP, Chao IM (1998) The impact of metaheuristics on solving the vehicle routing problem: algorithms, problem sets, and computational results. In T. G. e. a. Crainic (Ed.), Fleet management and logistics (pp. 33–56): Springer US.

  40. Göthe-Lundgren M, Jörnsten K, Värbrand P (1996) On the nucleolus of the basic vehicle routing game. Math Program 72(1):83–100

    MathSciNet  MATH  Google Scholar 

  41. Granot D, Huberman G (1981) Minimum cost spanning tree games. Math Program 21(1):1–18

    MathSciNet  MATH  Google Scholar 

  42. Han, Z. (2012). Game theory in wireless and communication networks: theory, models, and applications: Cambridge University Press.

  43. Hong L (2012) An improved LNS algorithm for real-time vehicle routing problem with time windows. Comput Oper Res 39(2):151–163

    MATH  Google Scholar 

  44. Hosseinabadi AAR, Rostami NSH, Kardgar M, Mirkamali S, Abraham A (2017) A new efficient approach for solving the capacitated vehicle routing problem using the gravitational emulation local search algorithm. Appl Math Modell. https://doi.org/10.1016/j.apm.2017.02.042

    Article  MathSciNet  MATH  Google Scholar 

  45. Jin J, Crainic TG, Løkketangen A (2014) A cooperative parallel metaheuristic for the capacitated vehicle routing problem. Comput Oper Res 44:33–41

    MathSciNet  MATH  Google Scholar 

  46. Kheirkhahzadeh M, Barforoush AA (2009) A hybrid algorithm for the vehicle routing problem. Paper presented at the Evolutionary Computation, 2009. CEC'09. IEEE Congress on.

  47. Kohout R, Erol K (1999) In-time agent-based vehicle routing with a stochastic improvement heuristic. In: Proceeding of the 16th Conference on Artificial Intelligence and the 11th on Innovative Applications of Artificial Intelligence (AAAI/IAAI 1999), 864–869. AAAI Press (1999).

  48. Koltsidas G, Pavlidou FN (2011) A game theoretical approach to clustering of ad-hoc and sensor networks. Telecommun Syst 47(1–2):81–93

    Google Scholar 

  49. Kruskal WH, Wallis WA (1952) Use of ranks in one-criterion variance analysis. J Am Stat Assoc 47(260):583–621

    MATH  Google Scholar 

  50. Kurve A, Griffin C, Kesidis G (2011). A graph partitioning game for distributed simulation of networks. Paper presented at the In Proceedings of the 2011 International Workshop on Modeling, Analysis, and Control of Complex Networks.

  51. Kytöjoki J, Nuortio T, Bräysy O, Gendreau M (2007) An efficient variable neighborhood search heuristic for very large scale vehicle routing problems. Comput Oper Res 34(9):2743–2757

    MATH  Google Scholar 

  52. Laporte G (2007) What you should know about the vehicle routing problem. Naval Res Log (NRL) 54(8):811–819

    MathSciNet  MATH  Google Scholar 

  53. Laporte G, Nobert Y (1987) Exact algorithms for the vehicle routing problem. North-Holland Math Stud 132:147–184

    MathSciNet  MATH  Google Scholar 

  54. Lima CDR, Goldbarg MC, Goldbarg EFG (2004) A memetic algorithm for the heterogeneous fleet vehicle routing problem. Elect Notes Dis Math 18:171–176

    MathSciNet  MATH  Google Scholar 

  55. Lin D, Wang Q, Lin D, Deng Y (2015) An energy-efficient clustering routing protocol based on evolutionary game theory in wireless sensor networks. Int J Dist Sens Netw 11(11):409503

    Google Scholar 

  56. Lin SW, Lee ZJ, Ying KC, Lee CY (2009) Applying hybrid meta-heuristics for capacitated vehicle routing problem. Expert Syst Appl 36(2):1505–1512

    Google Scholar 

  57. Lysgaard J, Letchford AN, Eglese RW (2004) A new branch-and-cut algorithm for the capacitated vehicle routing problem. Math Program 100(2):423–445

    MathSciNet  MATH  Google Scholar 

  58. Mester D, Bräysy O (2007) Active-guided evolution strategies for large-scale capacitated vehicle routing problems. Comput Oper Res 34(10):2964–2975

    MATH  Google Scholar 

  59. Milano M, Roli A (2004) MAGMA: a multiagent architecture for metaheuristics. IEEE Trans Syst Man Cybernet Part B (Cybernet), 34(2), 925–941.

  60. Monderer D, Shapley LS (1996) Potential games. Games Econ Behav 14(1):124–143

    MathSciNet  MATH  Google Scholar 

  61. Monostori L, Váncza J, Kumara SR (2006) Agent-based systems for manufacturing. CIRP Ann Manuf Technol 55(2):697–720

    Google Scholar 

  62. Naddef D, Rinaldi G (2002) Branch-and-cut algorithms for the capacitated VRP. In: Toth P, Vigo D (eds) The vehicle routing problem. SIAM monographs on discrete mathematics and applications, Philadelphia, pp 53–84

    MATH  Google Scholar 

  63. Narayanam R, Narahari Y (2012) A game theory inspired, decentralized, local information based algorithm for community detection in social graphs. Paper presented at the Pattern Recognition (ICPR), 2012 21st International Conference on

  64. Nazif H, Lee LS (2012) Optimised crossover genetic algorithm for capacitated vehicle routing problem. Appl Math Model 36(5):2110–2117

    MathSciNet  MATH  Google Scholar 

  65. Neel J, Buehrer RM, Reed B, Gilles RP (2002) Game theoretic analysis of a network of cognitive radios. Paper presented at the Circuits and Systems, 2002. MWSCAS-2002. The 2002 45th Midwest Symposium on.

  66. Ng K, Lee C, Zhang S, Wu K, Ho W (2017) A multiple colonies artificial bee colony algorithm for a capacitated vehicle routing problem and re-routing strategies under time-dependent traffic congestion. Comput Ind Eng 109:151–168

    Google Scholar 

  67. Nisan N, Roughgarden T, Tardos E, Vazirani V (2007) Algorithmic game theory cambridge university press. NY, USA, New York

    Google Scholar 

  68. Osman IH (1993) Metastrategy simulated annealing and tabu search algorithms for the vehicle routing problem. Ann Oper Res 41(4):421–451

    MATH  Google Scholar 

  69. Parunak HVD (1999) Industrial and practical applications of DAI. Multiagent systems: a modern approach to distributed artificial intelligence, 337–421.

  70. Pessoa A, De Aragão MP, Uchoa E (2008) Robust branch-cut-and-price algorithms for vehicle routing problems. In The vehicle routing problem: Latest advances and new challenges (pp. 297–325): Springer.

  71. Pisinger D, Ropke S (2009). Large neighborhood search. In M. Gendreau & J.-Y. Potvin (Eds.), Handbook of Metaheuristics (2 ed.).

  72. Prins C (2009) A GRASP× evolutionary local search hybrid for the vehicle routing problem. In Bio-inspired algorithms for the vehicle routing problem. Springer, Berlin Heidelberg, pp 35–53

    Google Scholar 

  73. Rochat Y, Taillard ÉD (1995) Probabilistic diversification and intensification in local search for vehicle routing. J Heurist 1(1):147–167

    MATH  Google Scholar 

  74. Rossit D G, Vigo D, Tohmé F, Frutos M (2016) Improving visual attractiveness in capacitated vehicle routing problems: a heuristic algorithm.

  75. Russell S, Norvig P (2010). Artificial Intelligence: A Modern Approach (Third Edition ed.). New Jersey: Prentice Hall, Englewood Cliffs.

  76. Sanchez-Soriano J, Lopez MA, Garcia-Jurado I (2001) On the core of transportation games. Math Soc Sci 41(2):215–225

    MathSciNet  MATH  Google Scholar 

  77. Shi H-Y, Wang W-L, Kwok N-M, Chen S-Y (2012) Game theory for wireless sensor networks: a survey. Sensors 12(7):9055–9097

    Google Scholar 

  78. Szeto WY, Wu Y, Ho SC (2011) An artificial bee colony algorithm for the capacitated vehicle routing problem. Eur J Oper Res 215(1):126–135

    Google Scholar 

  79. Teoh BE, Ponnambalam S, Kanagaraj G (2015) Differential evolution algorithm with local search for capacitated vehicle routing problem. Int J Bio-Insp Comput 7(5):321–342

    Google Scholar 

  80. Teymourian E, Kayvanfar V, Komaki GM, Zandieh M (2016) Enhanced intelligent water drops and cuckoo search algorithms for solving the capacitated vehicle routing problem. Inf Sci 334:354–378

    Google Scholar 

  81. Toth P, Vigo D (2003) The granular tabu search and its application to the vehicle-routing problem. INFORMS J Comput 15(4):333–346

    MathSciNet  MATH  Google Scholar 

  82. Toth P, Vigo D (2014) Vehicle routing: problems, methods, and applications (P. Toth & D. Vigo Eds. Vol. 18): Siam.

  83. Uchoa E, Pecin D, Pessoa A, Poggi M, Subramanian A, Vidal T (2017) New benchmark instances for the capacitated vehicle routing problem. Eur J Oper Res 257(3):845–858

    MathSciNet  MATH  Google Scholar 

  84. Vidal T (2015) Arc routing, vehicle routing, and turn penalties: multiple problems–one combined neighborhood. In Technical Report: Pontifcia Universidade Catlica do Rio de Janeiro.

  85. Vidal T, Crainic TG, Gendreau M, Lahrichi N, Rei W (2012) A hybrid genetic algorithm for multidepot and periodic vehicle routing problems. Oper Res 60(3):611–624

    MathSciNet  MATH  Google Scholar 

  86. Vidal T, Crainic TG, Gendreau M, Prins C (2014) Implicit depot assignments and rotations in vehicle routing heuristics. Eur J Oper Res 237(1):15–28

    MathSciNet  MATH  Google Scholar 

  87. Vidal T, Maculan N, Ochi LS, Vaz Penna PH (2015) Large neighborhoods with implicit customer selection for vehicle routing problems with profits. Transp Sci 50(2):720–734

    Google Scholar 

  88. Vokřínek J, Komenda A, Pechoucek M (2010) Agents towards vehicle routing problems. Proc. of 9th Int. Conf. on Autonomous Agents and Multiagent Systems (AAMAS 2010), van der Hoek, Kaminka, Lespérance, Luck and Sen (eds.), May, 10–14, 2010, Toronto, Canada, 773–780.

  89. Wang C-H, Lu J-Z (2009) A hybrid genetic algorithm that optimizes capacitated vehicle routing problems. Expert Syst Appl 36(2):2921–2936

    Google Scholar 

  90. Wooldridge M (2009) An introduction to multiagent systems. Wiley, Hoboken

    Google Scholar 

  91. Xie D, Sun Q, Zhou Q, Qiu Y, Yuan X (2013) An efficient clustering protocol for wireless sensor networks based on localized game theoretical approach. Int J Dist Sens Netw 9(8):476313

    Google Scholar 

  92. Yang L, Lu YZ, Zhong YC, Wu XG, Xing SJ (2016) A hybrid, game theory based, and distributed clustering protocol for wireless sensor networks. Wireless Netw 22(3):1007–1021

    Google Scholar 

  93. Yousefikhoshbakht M, Khorram E (2012) Solving the vehicle routing problem by a hybrid meta-heuristic algorithm. J Indus Eng Int 8(1):11

    Google Scholar 

  94. Yu B, Yang Z-Z, Yao B (2009) An improved ant colony optimization for vehicle routing problem. Eur J Oper Res 196(1):171–176

    MATH  Google Scholar 

  95. Yurtkuran A, Emel E (2010) A new hybrid electromagnetism-like algorithm for capacitated vehicle routing problems. Expert Syst Appl 37(4):3427–3433

    Google Scholar 

  96. Zachariadis EE, Kiranoudis CT (2010) A strategy for reducing the computational complexity of local search-based methods for the vehicle routing problem. Comput Oper Res 37(12):2089–2105

    Google Scholar 

  97. Zeddini B, Temani M, Yassine A, Ghedira K (2008). An agent-oriented approach for the dynamic vehicle routing problem. Paper presented at the In Advanced Information Systems for Enterprises, 2008. IWAISE'08.

  98. Zhang X, Tang L (2009) A new hybrid ant colony optimization algorithm for the vehicle routing problem. Pattern Recogn Lett 30(9):848–855

    Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Computer Engineering, University of Bonab, Bonab, Iran

    Mir Mohammad Alipour & Hojjat Emami

  2. Department of Mathematics, Faculty of Basic Science, University of Bonab, Bonab, Iran

    Mohsen Abdolhosseinzadeh

Authors
  1. Mir Mohammad Alipour
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Hojjat Emami
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Mohsen Abdolhosseinzadeh
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Mir Mohammad Alipour.

Ethics declarations

Conflict of interest

We (Mir Mohammad Alipour, HojjatEmami and Mohsen Abdolhosseinzadeh) wish to confirm that there are no known conflicts of interest associated with this article and there has been no significant financial support for this work that could have influenced its outcome.

Ethical approval

This article does not contain any studies with human participants or animals performed by any of the authors.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Alipour, M.M., Emami, H. & Abdolhosseinzadeh, M. A MAS approach for vehicle routing problem. Neural Comput & Applic 34, 4387–4411 (2022). https://doi.org/10.1007/s00521-021-06587-2

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00521-021-06587-2

Keywords

Search

Navigation