Skip to main content

Advertisement

SpringerLink
Log in

Applications of metaheuristic algorithms for optimal operation of cascaded hydropower plants

  • Original Article
  • Published:
Neural Computing and Applications Aims and scope Submit manuscript

Abstract

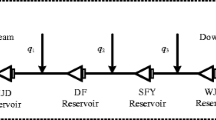
In this paper, two optimal operation plans of a cascaded reservoir system with four hydropower plants are studied for reaching the highest power energy of all the power plants. In the first plan, called local optimization plan, optimal water discharge of each upstream hydropower plant is determined first and the optimal discharge is then used as input data for determining optimal water discharge of other downstream hydropower plants. In the second plan, called global optimization plan, optimal water discharge of all hydropower plants is simultaneously determined. For reaching the highest total power energy of the system, nine methods consisting of moth swarm algorithm, Harris hawks optimization, cuckoo search algorithm (CSA), snap drift cuckoo search algorithm (SD-CSA), stochastic fractal search algorithm, parasitism predation algorithm, marine predator algorithm, tunicate swarm algorithm, and the proposed improved cuckoo search algorithm (ICSA) are implemented. Among the methods, the proposed ICSA is first developed by improving the exploitation phase of CSA. The comparisons of power energy from each hydropower plant for the two plans indicate that local optimization plan is more useful for upstream plants but for downstream plants, whereas global optimization plan is more useful for downstream plants. For the purpose of reaching the highest total power energy for the whole system, the global optimization plan is more effective because it reaches higher power energy than local optimization plan. For investigating the improvement of the proposed method over CSA and SD-CSA, the three methods are run for seven benchmark functions and for the global optimization plan with different population sizes and different iteration numbers. As a result, it is recommended that global optimization plan should be applied for all hydropower plants in cascaded systems and downstream plants with higher power energy can share benefit to upstream ones. In addition, one of the most effective methods that should be recommended for implementing global optimization plan is the proposed ICSA.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15
Fig. 16
Fig. 17
Fig. 18
Fig. 19

Similar content being viewed by others

Data availability

Data of the whole system were taken from [24] and also reported in “Appendix”.

Abbreviations

Infh,m :

Inflow into the hth hydropower plant at the mth interval

M :

Number of intervals

N hp :

Number of hydropower plants in the cascaded system

NoS:

Population

Nestk, Nesth, Nestn, Nestm, Nestp, Nestq :

Randomly chosen solutions from current population

\( P_{h}^{\hbox{min} } ,\,P_{h}^{\hbox{max} } \) :

Lower limit and upper limit of power output of the hth hydropower plant

\( {\text{RV}}_{h}^{\hbox{min} } ,\,{\text{RV}}_{h}^{\hbox{max} } \) :

Lower limit and upper limit of water volume of the hth reservoir

RVh,m :

Water volume of the hth reservoir at the end of the mth interval

RVh,m−I :

Reservoir volume of the hth hydropower plant at the (m-1)th interval

S E :

Sum of energy obtained by four hydropower plants

SWh,m :

Spillage water from the hth hydropower plant at the mth interval

T m :

Number of hours for the mth interval

T j,h :

Traveling time of water from the jth reservoir to the hth reservoir

\( {\text{WD}}_{h}^{\hbox{min} } ,\,{\text{WD}}_{h}^{\hbox{max} } \) :

Lower limit and upper limit of water discharge via turbine of the hth hydropower plant

WDh,m :

Water discharge via turbine of the hth hydropower plant at the mth interval

\( \varphi_{1,h} ,\,\varphi_{2,h} ,\,\varphi_{3,h} ,\,\varphi_{4,h} ,\,\varphi_{5,h} ,\varphi_{6,h} \) :

Coefficients of power generation function of the hth hydropower plant

WDs,1,M, WDs,2,M, WDs,3,M, WDs,4,M :

Water discharge of four hydropower plants at the Mth interval corresponding to the sth solution

RVs,1,M, RVs,2,M, RVs,3,M, RVs,4,M :

Reservoir volume of the four hydropower plants at the Mth interval corresponding to the sth solution

P s,1,M, P s,2,M, P s,3,M, P s,4,M :

Power generation of the four hydropower plants at the Mth interval corresponding to the sth solution

References

  1. Mandal KK, Basu M, Chakraborty N (2008) Particle swarm optimization technique based short-term hydrothermal schedulin. Appl Soft Comput 8(4):1392–1399

    Google Scholar 

  2. Wang Y, Zhou J, Mo L, Zhang R, Zhang Y (2012) Short-term hydrothermal generation scheduling using differential real-coded quantum-inspired evolutionary algorithm. Energy 44(1):657–671

    Google Scholar 

  3. Basu M (2011) Artificial immune system for fixed head hydrothermal power system. Energy 36(1):606–612

    Google Scholar 

  4. Das S, Bhattacharya A, Chakraborty AK (2018) Fixed head short-term hydrothermal scheduling in presence of solar and wind power. Energy Strategy Rev 22:47–60

    Google Scholar 

  5. Nguyen TT, Vo DN (2019) The application of an effective cuckoo search algorithm for optimal scheduling of hydrothermal system considering transmission constraints. Neural Comput Appl 31(8):4231–4252

    Google Scholar 

  6. Gupta R, Chowdhury N, Billinton R (1996) Economic impact of nonutility generation on hydrothermal systems with variable head hydro units. In: Proceedings of 1996 Canadian conference on electrical and computer engineering, vol. 1, pp 404–407

  7. Rashid AHA, Nor KM (1993) An algorithm for the optimal scheduling of variable head hydro and thermal plants. IEEE Trans Power Syst 8(3):1242–1249

    Google Scholar 

  8. Farhat IA, El-Hawary ME (2011) Scheduling of variable-head hydro-thermal generation using an enhanced bacterial foraging algorithm. In: 2011 24th Canadian conference on electrical and computer engineering, pp 436–44

  9. Salama MM, Elgazer MM, Abdelmaksoud SM, Henry HA (2013) Variable head hydrothermal generation scheduling using genetic algorithm and constriction factor based particle swarm optimization technique. Int Organ Sci Res J Eng 3(9):1–16

    Google Scholar 

  10. Gupta S, Narang N (2015) Integrated PSO-SQP technique for short term hydrothermal scheduling. Int J Adv Res Comput Eng Technol 4(4):1423–1428

    Google Scholar 

  11. Wang C, Shahidehpour SM (1993) Power generation scheduling for multi-area hydro-thermal systems with tie line constraints, cascaded reservoirs and uncertain data. IEEE Trans Power Syst 8(3):1333–1340

    Google Scholar 

  12. Soares S, Lyra C, Tavares H (1980) Optimal generation scheduling of hydrothermal power systems. IEEE Trans Power Appar Syst 3:1107–1118

    MATH  Google Scholar 

  13. Wardlaw R, Sharif M (1999) Evaluation of genetic algorithms for optimal reservoir system operation. J Water Resour Plan Manag 125(1):25–33

    Google Scholar 

  14. Tang X, Zhou J (2012) A future role for cascade hydropower in the electricity system of China. Energy Policy 51:358–363

    Google Scholar 

  15. Mo L, Lu P, Wang C, Zhou J (2013) Short-term hydro generation scheduling of Three Gorges–Gezhouba cascaded hydropower plants using hybrid MACS-ADE approach. Energy Convers Manag 76:260–273

    Google Scholar 

  16. Nguyen TT, Vo DN, Truong AV (2014) Cuckoo search algorithm for short-term hydrothermal scheduling. Appl Energy 132:276–287

    Google Scholar 

  17. Özyön S, Yaşar C (2018) Gravitational search algorithm applied to fixed head hydrothermal power system with transmission line security constraints. Energy 155:392–407

    Google Scholar 

  18. Sinha N, Chakrabarti R, Chattopadhaya PK (2003) Fast evolutionary programming techniques for short-term hydrothermal scheduling. Electric Power Syst. Res 66:97–103

    Google Scholar 

  19. Yu B, Yuan X, Wang J (2007) Short-term hydro-thermal scheduling using particle swarm optimization method. Energy Convers Manag 48:1902–1908

    Google Scholar 

  20. Yuan X, Wang L, Yuan Y (2008) Application of enhanced PSO approach to optimal scheduling of hydro system. Energy Convers Manag 49(11):2966–2972

    Google Scholar 

  21. Hotaa PK, Barisal AK, Chakrabarti R (2009) An improved PSO technique for short-term optimal hydrothermal scheduling. Electr Power Syst Res 79:1047–1053

    Google Scholar 

  22. Tavakoli HB, Mozafari B (2012) Short-term hydrothermal scheduling via honey-bee mating optimization algorithm. In: Power and energy engineering conference (APPEEC), Asia-Pacific, pp 1–5

  23. Fang N, Zhou J, Ma J (2014) Short-term Hydrothermal scheduling based on adaptive chaotic real coded genetic algorithm. In: IEEE conference on intelligent control and automation, pp 3412–3416

  24. Naresh R, Sharma J (1999) Two-phase neural network based solution technique for short term hydrothermal scheduling. IEEE Proc Gener Transm Distrib 146(6):657–663

    Google Scholar 

  25. Basu M, Datta S (2012) Biogeography-based optimization for short-term hydrothermal scheduling. In: Emerging trends in electrical engineering and energy management (ICETEEEM), international conference, pp 38–43

  26. Wang Y, Zhou J, Zhou C, Wang Y, Qin H, Lu Y (2012) An improved self-adaptive PSO technique for short-term hydrothermal scheduling. Expert Syst Appl 39:2288–2295

    Google Scholar 

  27. Roy PK, Sur A, Pradhan DK (2013) Optimal short-term hydro-thermal scheduling using quasi-oppositional teaching learning based optimization. Eng Appl Artif Intell 26:2516–2524

    Google Scholar 

  28. Rasoulzadeh-akhijahani A, Mohammadi-ivatloo B (2015) Short-term hydrothermal generation scheduling by a modified dynamic neighborhood learning based particle swarm optimization. Electr Power Energy Syst 67:350–367

    Google Scholar 

  29. Mohamed AAA, Mohamed YS, El-Gaafary AA, Hemeida AM (2017) Optimal power flow using moth swarm algorithm. Electr Power Syst Res 142:190–206

    Google Scholar 

  30. Heidari AA, Mirjalili S, Faris H, Aljarah I, Mafarja M, Chen H (2019) Harris hawks optimization: algorithm and applications. Future Gener Comput Syst 97:849–872

    Google Scholar 

  31. Yang XS, Deb S (2009) Cuckoo search via Lévy flights. In: 2009 World congress on nature & biologically inspired computing, pp 210–214

  32. Rakhshani H, Rahati A (2017) Snap-drift cuckoo search: a novel cuckoo search optimization algorithm. Appl Soft Comput 52:771–794

    MATH  Google Scholar 

  33. Salimi H (2015) Stochastic fractal search: a powerful metaheuristic algorithm. Knowl Based Syst 75:1–18

    Google Scholar 

  34. Mohamed AAA, Hassan SA, Hemeida AM, Alkhalaf S, Mahmoud MMM, Eldin AMB (2020) Parasitism–predation algorithm (PPA): a novel approach for feature selection. Ain Shams Eng J 11(2):293–308

    Google Scholar 

  35. Faramarzi A, Heidarinejad M, Mirjalili S, Gandomi AH (2020) Marine predators algorithm: a nature-inspired metaheuristic. Expert Syst Appl 152:113377

    Google Scholar 

  36. Kaur S, Awasthi LK, Sangal AL, Dhiman G (2020) Tunicate swarm algorithm: a new bio-inspired based metaheuristic paradigm for global optimization. Eng Appl Artif Intell 90:103541

    Google Scholar 

  37. Yang XS (2014) Nature-inspired optimization algorithms, 1st edn. Elsevier, Amsterdam

    MATH  Google Scholar 

  38. Yang XS, Deb S (2010) Engineering optimization by cuckoo search. Int J Math Model Numer Optim 1(4):339–343

    MATH  Google Scholar 

  39. Khan NA, Ahmad S, Razzaq OA, Ayaz M (2020) Rational approximation with cuckoo search algorithm for multifarious Painlevé type differential equations. Ain Shams Eng J 11(1):179–190

    Google Scholar 

  40. Ding J, Qunjin W, Qian Z, Qiubo Y, Yuan M (2019) A hybrid particle swarm optimization-cuckoo search algorithm and its engineering applications. Math Probl Eng 2019:1–12

    MATH  Google Scholar 

  41. Ahmed J, Salam Z (2014) A maximum power point tracking (MPPT) for PV system using Cuckoo search with partial shading capability. Appl Energy 119:118–130

    Google Scholar 

  42. Afzalan E, Joorabian M (2015) An improved cuckoo search algorithm for power economic load dispatch. Int Trans Electr Energy Syst 25(6):958–975

    Google Scholar 

  43. Meng X, Chang J, Wang X, Wang Y (2019) Multi-objective hydropower station operation using an improved cuckoo search algorithm. Energy 168:425–439

    Google Scholar 

  44. Ong P, Zainuddin Z (2019) Optimizing wavelet neural networks using modified cuckoo search for multi-step ahead chaotic time series prediction. Appl Soft Comput 80:374–386

    Google Scholar 

  45. Nguyen TT, Nguyen TT, Vo DN (2018) An effective cuckoo search algorithm for large-scale combined heat and power economic dispatch problem. Neural Comput Appl 30(11):3545–3564

    Google Scholar 

  46. Nguyen TT, Vo DN, Dinh BH (2018) An effectively adaptive selective cuckoo search algorithm for solving three complicated short-term hydrothermal scheduling problems. Energy 155:930–956

    Google Scholar 

  47. Yang B, Miao J, Fan Z, Long J, Liu X (2018) Modified cuckoo search algorithm for the optimal placement of actuators problem. Appl Soft Comput 67:48–60

    Google Scholar 

  48. Zhang Y, Zhao H, Cao Y, Liu Q, Shen Z, Wang J, Hu M (2018) A hybrid ant colony and Cuckoo search algorithm for route optimization of heating engineering. Energies 11(10):2675

    Google Scholar 

  49. Zhang X, Wan Q, Fan Y (2019) Applying modified cuckoo search algorithm for solving systems of nonlinear equations. Neural Comput Appl 31(2):553–576

    Google Scholar 

  50. Kang T, Yao J, Jin M, Yang S, Duong T (2018) A novel improved cuckoo search algorithm for parameter estimation of photovoltaic (PV) models. Energies 11(5):1060

    Google Scholar 

  51. Xiao L, Dridi M, Hajjam El Hassani A, Fei H, Lin W (2018) An improved cuckoo search for a patient transportation problem with consideration of reducing transport emissions. Sustainability 10(3):793

    Google Scholar 

  52. Nguyen TT, Nguyen CT, Le VD, Nguyen QV (2019) Finding optimal load dispatch solutions by using a proposed cuckoo search algorithm. Math Probl Eng 2019:1–29

    MathSciNet  MATH  Google Scholar 

  53. Yu J, Kim C, Rhee S (2020) Clustering cuckoo search optimization for economic load dispatch problem. Neural Comput Appl. (article in press)

  54. http://www.socscistatistics.com/tests/signedranks/Default2.aspx

  55. Derrac J, García S, Molina D, Herrera F (2011) A practical tutorial on the use of nonparametric statistical tests as a methodology for comparing evolutionary and swarm intelligence algorithms. Swarm Evol Comput 1(1):3–18

    Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Power System Optimization Research Group, Faculty of Electrical and Electronics Engineering, Ton Duc Thang University, Ho Chi Minh City, Vietnam

    Thang Trung Nguyen

  2. Faculty of Electrical Engineering Technology, Industrial University of Ho Chi Minh City, Ho Chi Minh City, Vietnam

    Thuan Thanh Nguyen

  3. Institute of Research and Development, Duy Tan University, Danang, 550000, Vietnam

    Thai Dinh Pham

Authors
  1. Thang Trung Nguyen
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Thuan Thanh Nguyen
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Thai Dinh Pham
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Thai Dinh Pham.

Ethics declarations

Conflict of interest

The authors declare that they have no conflict of interest.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Appendix

Appendix

See Tables 8, 9, 10, 11 and 12.

Table 8 Hydraulic limitations of four reservoirs (\( \times \) 104 m3)
Full size table
Table 9 Power output function coefficients of four hydropower plants
Full size table
Table 10 Inflows of four reservoirs (× 104 m3)
Full size table
Table 11 Travelling time (in hour) from upstream to downstream reservoirs
Full size table
Table 12 Optimal water discharge (× 104 m3) found by the proposed method
Full size table

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Nguyen, T.T., Nguyen, T.T. & Pham, T.D. Applications of metaheuristic algorithms for optimal operation of cascaded hydropower plants. Neural Comput & Applic 33, 6549–6574 (2021). https://doi.org/10.1007/s00521-020-05418-0

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00521-020-05418-0

Keywords

Search

Navigation