Skip to main content
SpringerLink
Log in

An online self-organizing algorithm for feedforward neural network

  • Original Article
  • Published:
Neural Computing and Applications Aims and scope Submit manuscript

Abstract

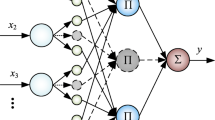
Feedforward neural network (FNN) is the most popular network model, and the appropriate structure and learning algorithms are the key of its performance. This paper proposes an online self-organizing algorithm for feedforward neural network (OSNN) with a single hidden layer. The proposed OSNN optimizes the structure of FNN for time-varying system including structure design and parameter learning. In structure design, this paper measures the contribution ratios of hidden nodes by local sensitivity analysis based on differentiation method. OSNN merges hidden nodes with the others that have the highest correlation when their contribution ratios are almost zero and adds new hidden nodes by error reparation. For parameter learning, an improved online gradient method (OGM), called online gradient method with fixed memory (FMOGM), is proposed to improve the convergence speed and accuracy of OGM. In addition, this paper calculates the contribution ratios and the network error and estimates the local minima by using the fixed-sized training set of FMOGM instead of one sample at the current time, which can obtain more effective local information and a compact network structure. Finally, the proposed OSNN is verified using a number of benchmark problems and a practical problem for biochemical oxygen demand prediction in wastewater treatment. The experimental results show that OSNN has better convergence speed and accuracy than other algorithms.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15

Similar content being viewed by others

References

  1. Chen WC, Tseng LY, Wu CS (2014) A unified evolutionary training scheme for single and ensemble of feedforward neural network. Neurocomputing 143:347–361

    Article  Google Scholar 

  2. Esfe MH, Afrand M, Wongwises S, Naderi A, Asadi A, Rostami S, Akbari M (2015) Applications of feedforward multilayer perceptron artificial neural networks and empirical correlation for prediction of thermal conductivity of Mg(OH)_2-EG sing experimental data. Int Commun Heat Mass Transf 67:46–50

    Article  Google Scholar 

  3. Wang N, Er MJ, Han M (2015) Generalized single-hidden layer feedforward networks for regression problems. IEEE Trans Neural Netw Learn Syst 26(6):1161–1176

    Article  MathSciNet  Google Scholar 

  4. Guliyev NJ, Ismailov VE (2018) On the approximation by single hidden layer feedforward neural networks with fixed weights. Neural Netw 98:296–304

    Article  MATH  Google Scholar 

  5. Hu JY, Zhangand JS, Zhang CX, Wang J (2016) A new deep neural network based on a stack of single-hidden-layer feedforward neural networks with randomly fixed hidden neurons. Neurocomputing 171:63–72

    Article  Google Scholar 

  6. Qiao JF, Zhang ZZ, Bo YC (2014) An online self-adaptive modular neural network for time-varying systems. Neurocomputing 125:7–16

    Article  Google Scholar 

  7. Oong TH, Isa NAM (2011) Adaptive evolutionary artificial neural network for pattern classification. IEEE Trans Neural Netw 22(11):1823–1836

    Article  Google Scholar 

  8. Ghime AM, Patriciu VV (2017) Neural network models in big data analytics and cyber security. In: 2017 9th International conference on electronics, computers and artificial intelligence (ECAI), pp 1–6

  9. Wu X, Róycki P, Wilamowski BM (2015) A hybrid constructive algorithm for single-layer feedforward networks learning. IEEE Trans Neural Netw Learn Syst 26(8):1659–1668

    Article  MathSciNet  Google Scholar 

  10. Qiao JF, Liand FJ, Han HG, Li WJ (2016) Constructive algorithm for fully connected cascade feedforward neural networks. Neurocomputing 182:154–164

    Article  Google Scholar 

  11. Liu D, Chang TS, Zhang Y (2002) A constructive algorithm for feedforward neural networks with incremental training. IEEE Trans Circuits Syst 49(12):1876–1879

    Article  Google Scholar 

  12. Fritzke B (1994) Growing cell structures a self-organizing network for unsupervised and supervised learning. Neural Netw 7(9):1441–1460

    Article  Google Scholar 

  13. Nielsen AB, Hansen LK (2008) Structure learning by pruning in independent component analysis. Neurocomputing 71(10–12):2281–2290

    Article  Google Scholar 

  14. Engelbrecht AP (2001) A new pruning heuristic based on variance analysis of sensitivity information. IEEE Trans Neural Netw 12(6):1386–1399

    Article  Google Scholar 

  15. Lauret P, Fock E, Mara TA (2006) A node pruning algorithm based on a Fourier amplitude sensitivity test method. IEEE Trans Neural Netw 17(2):273–293

    Article  Google Scholar 

  16. Han HG, Chen ZY, Liu HX (2018) A self-organizing interval Type-2 fuzzy-neural- network for modeling nonlinear systems. Neurocomputing 290:196–207

    Article  Google Scholar 

  17. Han HG, Wu XL, Qiao JF (2014) Nonlinear systems modeling based on self-organizing fuzzy-neural-network with adaptive computation algorithm. IEEE Trans Cybern 44(4):554–564

    Article  Google Scholar 

  18. Qiao JF, Li SY, Han HG, Wang DH (2017) An improved algorithm for building self-organizing feedforward neural networks. Neurocomputing 262:28–48

    Article  Google Scholar 

  19. Hsu CF (2008) Adaptive growing-and-pruning neural network control for a linear piezoelectric ceramic motor. Eng Appl Artif Intell 21(8):1153–1163

    Article  Google Scholar 

  20. Islamand MM, Sattarand MA, Aminand MF, Yaoand X, Murase K (2009) A new adaptive merging and growing algorithm for designing artificial neural networks. IEEE Trans Syst Man Cybern 39(3):705–722

    Article  Google Scholar 

  21. Han HG, Qiao JF (2013) A structure optimisation algorithm for feedforward neural network construction. Neurocomputing 99:347–357

    Article  Google Scholar 

  22. Zhang HH, Wu W, Liu F, Yao M (2009) Boundedness and convergence of online gradient method with penalty for feedforward neural networks. IEEE Trans Neural Netw 20(6):1050–1054

    Article  Google Scholar 

  23. Borgonovo E, Plischke E (2016) Sensitivity analysis: a review of recent advances. Eur J Oper Res 248(3):869–887

    Article  MathSciNet  MATH  Google Scholar 

  24. Xu CG, Gertner GZ (2008) Uncertainty and sensitivity analysis for models with correlated parameters. Reliability Engineering \& System Safety 93(10):1563-1573

  25. Wu W, Wang J, Cheng MS, Li ZX (2011) Convergence analysis of online gradient method for BP neural networks. Neural Netw 24(1):91–98

    Article  MATH  Google Scholar 

  26. Wu W, Feng GR, Li ZX, Xu YS (2005) Deterministic convergence of an online gradient method for BP neural networks. IEEE Trans Neural Netw 16(3):533–540

    Article  Google Scholar 

  27. Shao HM, Zheng GF (2011) Boundedness and convergence of online gradient method with penalty and momentum. Neurocomputing 74(5):765–770

    Article  Google Scholar 

  28. Liang NY, Huang GB, Sundararajan N (2006) A fast and accurate online sequential learning algorithm for feedforward networks. IEEE Trans Neural Netw 17(6):1411–1423

    Article  Google Scholar 

  29. Huynh HT, Won YW (2011) Regularized online sequential learning algorithm for single-hidden layer feedforward neural networks. Pattern Recogn Lett 32(14):1930–1935

    Article  Google Scholar 

  30. Wang XY, Han M (2014) Online sequential extreme learning machine with kernels for nonstationary time series prediction. Neurocomputing 145:90–97

    Article  Google Scholar 

  31. Wang JL, Belatreche A, Maguire L, McGinnity TM (2014) An online supervised learning method for spiking neural networks with adaptive structure. Neurocomputing 144:526–536

    Article  Google Scholar 

  32. Dora S, Subramanian K, Suresh S, Sundararajan N (2016) Development of a self-regulating evolving spiking neural network for classification problem. Neurocomputing 171:1216–1229

    Article  Google Scholar 

  33. Han HG, Zhang S, Qiao JF (2017) An adaptive growing and pruning algorithm for designing recurrent neural network. Neurocomputing 242:51–62

    Article  Google Scholar 

  34. Huang GB, Saratchandran P, Sundarajan N (2011) An efficient sequential learning algorithm for growing and pruning RBF (GAP-RBF) networks. IEEE Trans Syst Man Cybern 34(6):2284–2292

    Article  Google Scholar 

  35. Han HG, Qiao JF (2009) Biological oxygen demand (BOD) soft measuring based on dynamic neural network (DNN): a simulation study. In: 2009 7th Asian control conference, pp 757–762

  36. Zhu J, Zurcher J, Rao M, Meng MQH (1998) An online wastewater quality prediction system based on a time-delay neural network. Eng Appl Artif Intell 11(6):747–758

    Article  Google Scholar 

Download references

Acknowledgements

This research was supported by the National Natural Science Foundation of China [Nos. 61890930-5, 61533002 and 61603009]; National Key Research and Development Project [No. 2018YFC1900800-5]; Beijing Natural Science Foundation [No. 4182007]; Beijing Municipal Education Commission Foundation [No. KM201910005023]; and “Rixin Scientist” Foundation of Beijing University of Technology [No. 2017-RX(1)-04].

Author information

Authors and Affiliations

  1. Faculty of Information Technology, Beijing University of Technology, Beijing, 100124, China

    Jun-fei Qiao, Xin Guo & Wen-jing Li

  2. Beijing Key Laboratory of Computational Intelligence and Intelligent System, Beijing, 100124, China

    Jun-fei Qiao, Xin Guo & Wen-jing Li

Authors
  1. Jun-fei Qiao
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Xin Guo
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Wen-jing Li
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Jun-fei Qiao.

Ethics declarations

Conflict of interest

The authors declare that they have no conflict of interest.

Ethical approval

This article does not contain any studies with human participants or animals performed by any of the authors.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Qiao, Jf., Guo, X. & Li, Wj. An online self-organizing algorithm for feedforward neural network. Neural Comput & Applic 32, 17505–17518 (2020). https://doi.org/10.1007/s00521-020-04907-6

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00521-020-04907-6

Keywords

Search

Navigation