Skip to main content
SpringerLink
Log in

A self-adaptive estimation of distribution algorithm with differential evolution strategy for supermarket location problem

  • Original Article
  • Published:
Neural Computing and Applications Aims and scope Submit manuscript

Abstract

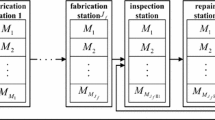
In modern production systems, an ever-rising product variety has imposed great challenges for in-plant part supply systems used to feed mixed-model assembly lines with required parts. In recent years, many automotive manufacturers have identified the supermarket concept as an efficient part feeding strategy to enable JIT (Just-in-time) deliveries at low costs. This paper studies a discrete supermarket location problem which considers the utilization rate and capacity constraint of the supermarkets simultaneously. Firstly, a mathematical model is developed with the objective of minimizing the total system cost consisting of operating cost and transportation cost. Then, a self-adaptive estimation of distribution algorithm with differential evolution strategy, named DE/AEDA, is proposed to solve the problem. Finally, computational experiments are carried out to analyze the performance of the proposed algorithm compared with the benchmark algorithm by using a non-parametric test method. The results indicate that the proposed algorithm is valid and efficient.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8

Similar content being viewed by others

References

  1. Shahabudeen P, Gopinath R, Krishnaiah K (2002) Design of bi-criteria kanban system using simulated annealing technique. Comput Ind Eng 41(4):355–370

    Article  Google Scholar 

  2. Wang J, Chang Q, Xiao G, Wang N, Li S (2011) Data driven production modeling and simulation of complex automobile general assembly plant. Comput Ind 62(7):765–775

    Article  Google Scholar 

  3. Battini D, Faccio M, Persona A, Sgarbossa F (2009) Framework to optimise the inventory centralisation/decentralisation degree and feeding policy in assembly systems. Int J Serv Oper Manag 6(2):184–205

    Google Scholar 

  4. Battini D, Boysen N, Emde S (2013) Just-in-Time supermarkets for part supply in the automobile industry. J Manag Control 24(2):209–217

    Article  Google Scholar 

  5. Emde S, Gendreau M (2017) Scheduling in-house transport vehicles to feed parts to automotive assembly lines. Eur J Oper Res 260(1):255–267

    Article  MathSciNet  MATH  Google Scholar 

  6. Emde S, Boysen N (2012) Optimally locating in-house logistics areas to facilitate JIT-supply of mixed-model assembly lines. Int J Prod Econ 135(1):393–402

    Article  Google Scholar 

  7. Vaidyanathan BS, Matson JO, Miller DM, Matson JE (1999) A capacitated vehicle routing problem for just-in-time delivery. IIE Trans 31(11):1083–1092

    Google Scholar 

  8. Emde S, Boysen N (2012) Optimally routing and scheduling tow trains for JIT-supply of mixed-model assembly lines. Eur J Oper Res 217(2):287–299

    MathSciNet  MATH  Google Scholar 

  9. Emde S, Fliedner M, Boysen N (2012) Optimally loading tow trains for just-in-time supply of mixed-model assembly lines. IIE Trans 44(2):121–135

    Article  Google Scholar 

  10. Golz J, Gujjula R, Günther HO, Rinderer S, Ziegler M (2012) Part feeding at high-variant mixed-model assembly lines. Flex Serv Manuf J 24(2):119–141

    Article  Google Scholar 

  11. Fathi M, Alvarez MJ, Hassanimehraban F, Rodríguez V (2014) A multiobjective optimization algorithm to solve the part feeding problem in mixed-model assembly lines. Math Probl Eng 2014(1):1–12

    Article  Google Scholar 

  12. Fathi M, Rodríguez V, Alvarez MJ (2014) A novel memetic ant colony optimization-based heuristic algorithm for solving the assembly line part feeding problem. Int J Adv Manuf Technol 75(1–4):629–643

    Article  Google Scholar 

  13. Fathi M, Rodríguez V, Fontes DB, Alvarez MJ (2016) A modified particle swarm optimisation algorithm to solve the part feeding problem at assembly lines. Int J Prod Res 54(3):878–893

    Article  Google Scholar 

  14. Alnahhal M, Noche B (2015) A genetic algorithm for supermarket location problem. Assem Autom 35(1):122–127

    Article  Google Scholar 

  15. Herda M (2015) Combined genetic algorithm for capacitated p-median problem. In: Computational intelligence and informatics (CINTI), 2015 16th IEEE international symposium on, IEEE, pp 151–154

  16. Arqub OA, Abo-Hammour Z (2014) Numerical solution of systems of second-order boundary value problems using continuous genetic algorithm. Inf Sci 279:396–415

    Article  MathSciNet  MATH  Google Scholar 

  17. Abo-Hammour Z, Abu Arqub O, Momani S, Shawagfeh N (2014) Optimization solution of Troesch’s and Bratu’s problems of ordinary type using novel continuous genetic algorithm. Discrete Dyn Nat Soc 2014:1–15

    Article  MathSciNet  MATH  Google Scholar 

  18. Abo-Hammour Z, Arqub OA, Alsmadi O, Momani S, Alsaedi A (2014) An optimization algorithm for solving systems of singular boundary value problems. Appl Math Inf Sci 8(6):2809–2821

    Article  MathSciNet  Google Scholar 

  19. Zhou BH, Shen CY (2018) Multi-objective optimization of material delivery for mixed model assembly lines with energy consideration. J Clean Prod 192:293–305

    Article  Google Scholar 

  20. Reese J (2006) Solution methods for the p-median problem: an annotated bibliography. Networks 48(3):125–142

    Article  MathSciNet  MATH  Google Scholar 

  21. Mladenović N, Brimberg J, Hansen P, Moreno-Pérez JA (2007) The p-median problem: a survey of metaheuristic approaches. Eur J Oper Res 179(3):927–939

    Article  MathSciNet  MATH  Google Scholar 

  22. Correa ES, Steiner MTA, Freitas AA, Carnieri C (2004) A genetic algorithm for solving a capacitated p-median problem. Numer Algorithms 35(2–4):373–388

    Article  MathSciNet  MATH  Google Scholar 

  23. França PM, Sosa NM, Pureza V (1999) An adaptive tabu search algorithm for the capacitated clustering problem. Int Trans Oper Res 6(6):665–678

    Article  MathSciNet  Google Scholar 

  24. Yaghini M, Karimi M, Rahbar M (2013) A hybrid metaheuristic approach for the capacitated p-median problem. Appl Soft Comput 13(9):3922–3930

    Article  Google Scholar 

  25. Landa-Torres I, Del Ser J, Salcedo-Sanz S, Gil-Lopez S, Portilla-Figueras JA, Alonso-Garrido O (2012) A comparative study of two hybrid grouping evolutionary techniques for the capacitated P-median problem. Comput Oper Res 39(9):2214–2222

    Article  MathSciNet  MATH  Google Scholar 

  26. Mühlenbein H, Paass G (1996) From recombination of genes to the estimation of distributions I. Binary parameters. In: International conference on parallel problem solving from nature, Springer, Berlin, Heidelberg, pp 178–187

  27. Zhou BH, Hu LM, Zhong ZY (2018) A hybrid differential evolution algorithm with estimation of distribution algorithm for reentrant hybrid flow shop scheduling problem. Neural Comput Appl 30(1):193–209

    Article  Google Scholar 

  28. Zhang Q, Sun J, Tsang E, Ford J (2006) Estimation of distribution algorithm with 2-opt local search for the quadratic assignment problem. In: Towards a new evolutionary computation, Springer, Berlin, Heidelberg, pp 281–292

  29. Tiwari A, Chang PC, Tiwari MK, Kollanoor NJ (2015) A Pareto block-based estimation and distribution algorithm for multi-objective permutation flow shop scheduling problem. Int J Prod Res 53(3):793–834

    Article  Google Scholar 

  30. Zhou BH, Tan F (2018) Electric vehicle handling routing and battery swap station location optimization for automotive assembly lines. Int J Comput Integr Manuf 31(10):978–991

    Article  Google Scholar 

  31. Wang L, Fang C (2012) An effective estimation of distribution algorithm for the multi-mode resource-constrained project scheduling problem. Comput Oper Res 39(2):449–460

    Article  Google Scholar 

  32. Aickelin U, Burke EK, Li J (2007) An estimation of distribution algorithm with intelligent local search for rule-based nurse rostering. J Oper Res Soc 58(12):1574–1585

    Article  MATH  Google Scholar 

  33. Zhang R, Song S, Wu C (2013) A hybrid artificial bee colony algorithm for the job shop scheduling problem. Int J Prod Econ 141(1):167–178

    Article  Google Scholar 

  34. Derrac J, García S, Molina D, Herrera F (2011) A practical tutorial on the use of nonparametric statistical tests as a methodology for comparing evolutionary and swarm intelligence algorithms. Swarm Evol Comput 1(1):3–18

    Article  Google Scholar 

Download references

Acknowledgements

This work was supported by the National Natural Science Foundation of China under Grant No. 71471135.

Funding

The authors appreciate the supports to this research from the National Natural Science Foundation of China under Grant No. 71471135.

Author information

Authors and Affiliations

  1. School of Mechanical Engineering, Tongji University, Shanghai, 201804, People’s Republic of China

    Bing-Hai Zhou & Fen Tan

Authors
  1. Bing-Hai Zhou
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Fen Tan
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Bing-Hai Zhou.

Ethics declarations

Conflict of interest

No potential conflict of interest was reported by the authors.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Zhou, BH., Tan, F. A self-adaptive estimation of distribution algorithm with differential evolution strategy for supermarket location problem. Neural Comput & Applic 32, 5791–5804 (2020). https://doi.org/10.1007/s00521-019-04052-9

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00521-019-04052-9

Keywords

Search

Navigation