Abstract
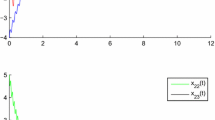
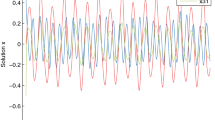
A multidirectional associative memory (MAM) neural network with periodic coefficients and distributed delays is studied. By constructing a Poincaré mapping, some sufficient conditions are obtained ensuring existence, uniqueness and the global exponential stability of a periodic solution of MAM neural network. The result is new to MAM neural networks. An example is given to illustrate the effectiveness of the result.

Similar content being viewed by others
References
Hagiwara M (1990) Multidirectional associative memory. In: Proceedings of international joint conference on neural networks, Washington, DC 1:3–6
Hattori M, Hagiwara M (2000) Associative memory for intelligent control. Math Comput Simul 51(3–4):349–374
Hattori M, Hagiwara M, Nakagawa M (1992) Improved multidirectional associative memories for training sets including common terms. In: Proceedings of international joint conference on neural networks, Baltimore 2:172–177
Huang J, Hagiwara M (2002) A combined multi-winner multidirectional associative memory. Neurocomputing 48(1):369–389
Hattori M, Hagiwara M (1998) Multimodule associative memory for many-to-many associations. Neurocomputing 19(1–3):99–119
Kosko B (1988) Bi-directional associative memories. IEEE Trans Syst Man Cybern 18(1):49–60
Chen S, Gao H (1998) Multivalued exponential multidirectional associative memory. J Softw 9(5):397–400
Wang M, Zhou T, Fang H (2010) Global exponential stability of MAM neural network with varying-time delays. In: Proc int conf comput intell soft eng, Wuhan 1:1–4
Zhou T, Wang M, Long M (2012) Existence and exponential stability of multiple periodic solutions for a multidirectional associative memory neural network. Neural Process Lett 35(2):187–202
Acknowledgments
This work was supported by the Natural Science Foundation of Hunan Province (Grant No. 06JJ2100) and the Science Foundation of Hunan Agricultural University (Grant No. 07WD08). The authors are grateful for the constructive comments of the referees.
Author information
Authors and Affiliations
Corresponding author
Appendix
Appendix
1.1 Proof of Lemma 1
Proof
Suppose \(x(t) = (x_{11}(t), \dots , x_{1n_1}(t), \dots , x_{m1}(t), \dots , x_{mn_m}(t))^T\) is a \(T\)-periodic solution of MAM (2). Then,
From assumption (H2) and the periodicity of \(x(t)\), we obtain
Therefore,
It implies that \(x(t)\) is a \(T\)-periodic solution of MAM (4). Now, if \(x(t)\) is a \(T\)-periodic solution of MAM (4), then one can reverse the above sequence of steps and show that \(x(t)\) is also a \(T\)-periodic solution of MAM (2).
1.2 Proof of Lemma 2
Proof
From assumption (H2), we have
and
Rights and permissions
About this article
Cite this article
Wang, Y., Wang, M. & Zhou, T. Existence, uniqueness and global exponential stability of a periodic solution for a class of multidirectional associative memory neural network models. Neural Comput & Applic 26, 979–986 (2015). https://doi.org/10.1007/s00521-014-1772-0
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00521-014-1772-0