Skip to main content
SpringerLink
Log in

Application of three unsupervised neural network models to singular nonlinear BVP of transformed 2D Bratu equation

  • Original Article
  • Published:
Neural Computing and Applications Aims and scope Submit manuscript

Abstract

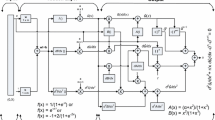
In this paper, numerical techniques are developed for solving two-dimensional Bratu equations using different neural network models optimized with the sequential quadratic programming technique. The original two-dimensional problem is transformed into an equivalent singular, nonlinear boundary value problem of ordinary differential equations. Three neural network models are developed for the transformed problem based on unsupervised error using log-sigmoid, radial basis and tan-sigmoid functions. Optimal weights for each model are trained with the help of the sequential quadratic programming algorithm. Three test cases of the equation are solved using the proposed schemes. Statistical analysis based on a large number of independent runs is carried out to validate the models in terms of accuracy, convergence and computational complexity.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9

Similar content being viewed by others

References

  1. Khan JA, Raja MAZ, Qureshi IM (2011) Stochastic computational approach for complex nonlinear ordinary differential equations. Chin Phys Lett 28(2):020206

    Article  MathSciNet  Google Scholar 

  2. Meada AJ, Fernandez AA (1994) The numerical solution of linear ordinary differential equation by feed forward neural network. Math Comput Model 19:1–25

    Article  Google Scholar 

  3. Yazdi HS, Pourreza R (2010) Unsupervised adaptive neural-fuzzy inference system for solving differential equations. Appl Soft Comput 10.1:267–275

    Article  Google Scholar 

  4. Shirvany Y, Hayati M, Moradian R (2009) Multilayer perceptron neural networks with novel unsupervised training method for numerical solution of the partial differential equations. Appl Soft Comput 9:20–29

    Article  Google Scholar 

  5. Khan JA, Raja MAZ, Qureshi IM (2011) Novel approach for van der Pol Oscillator on the continuous time domain. Chin Phys Lett 28:110205. doi:10.1088/0256-307X/28/11/110205

    Article  Google Scholar 

  6. Khan JA, Raja MAZ, Qureshi IM (2011) Hybrid evolutionary computational approach: application to van der Pol oscillator. Int J Phys Sci 6(31):7247–7261

    Google Scholar 

  7. Effati, S, Pakdaman M (2012) Optimal control problem via neural networks. Neural Comput Appl pp 1–8

  8. Raja MAZ, Samar R (2014) Numerical Treatment for nonlinear MHD Jeffery-Hamel problem using Neural Networks Optimized with Interior Point Algorithm. Neurocomputing 124:178–193. doi:10.1016/j.neucom.2013.07.013

    Article  Google Scholar 

  9. Raja MAZ, Samar R (2014) Numerical treatment of nonlinear MHD Jeffery-Hamel problems using stochastic algorithms. Comput Fluids 91:28–46

    Article  MathSciNet  Google Scholar 

  10. Monterola C, Saloma C (2001) Solving the nonlinear Schrodinger equation with an unsupervised neural network. Opt Exp 9(2):72–84

    Article  Google Scholar 

  11. Raja MAZ, Khan JA, Qureshi IM (2013) Numerical treatment for Painlevé Equation I using neural networks and stochastic solvers. Innov Intell Mach 3. Springer, Berlin, pp103–117

  12. Raja MAZ, Khan JA, Ahmad SI, Qureshi IM (2012) Solution of the Painlevé Equation-I using neural network optimized with swarm intelligence. Comput Intell Neurosci ID 721867 Vol. 2012, p 10

  13. Raja MAZ (2014) Unsupervised neural networks for solving Troesch’s problem. Chin Phys B 23(1):018903

    Article  Google Scholar 

  14. Raja MAZ Stochastic numerical techniques for solving Troesh’s problem. Accepted in Information Sciences. doi:10.1016/j.ins.2014.04.036

  15. Raja MAZ, Ahmad SI (2014) Numerical treatment for solving one-dimensional Bratu Problem using Neural networks. Neural Comput Appl 24(3–4):549–561. doi:10.1007/s00521-012-1261-2

    Article  Google Scholar 

  16. Raja MAZ Solution of one-dimension Bratu equation arising in fuel ignition model using ANN optimized with PSO and SQP, Accepted in Connection Science, 17-04-14. doi:10.1080/09540091.2014.907555

  17. Khan JA, Raja MAZ, Qureshi IM (2011) Numerical treatment of nonlinear Emden-Fowler equation using stochastic technique. Ann Math Artif Intell 63(2):185–207

    Article  MathSciNet  Google Scholar 

  18. Raja MAZ, Khan JA, Qureshi IM (2010) Evolutionary computational intelligence in solving the fractional differential equations. In: Intelligent Information and Database Systems. Springer Berlin Heidelberg, pp 231–240

  19. Raja MAZ, Khan JA, Qureshi IM (2011) Swarm Intelligent optimized neural networks for solving fractional differential equations. Int J Innov Comput Inf Control 7(11):6301–6318

    Google Scholar 

  20. Raja MAZ, Khan JA, Qureshi IM (2010) A new stochastic approach for solution of Riccati differential equation of fractional order. Ann Math Artif Intell 60(3–4):229–250

    Article  MATH  MathSciNet  Google Scholar 

  21. Raja MAZ, Khan JA, Qureshi IM (2011) Solution of fractional order system of Bagley-Torvik equation using evolutionary computational intelligence. Math Prob Eng, vol. 2011, Article ID. 675075, p 18

  22. Raja MAZ, Ahmad SI, Samar R (2012) Neural network optimized with evolutionary computing technique for solving the 2-dimensional Bratu problem. Neural Comput Appl. doi:10.1007/s00521-012-1170-4

    Google Scholar 

  23. MAZ Raja, Ahmad SI, Samar R Solution of the 2-Dimensional Bratu Problem using neural network, Swarm Intelligence and Sequential Quadratic Programming, Neural Comput Appl, submitted on 06-03-2013

  24. Curtis FE, Overton ML (2012) A sequential quadratic programming algorithm for nonconvex, nonsmooth constrained optimization. SIAM J Optim 22(2):474–500

    Article  MATH  MathSciNet  Google Scholar 

  25. Gill PE, Wong E (2012) Sequential quadratic programming methods. In: Mixed integer nonlinear programming. Springer New York, pp 147–224

  26. Nocedal J, Wright SJ (2006) Numerical optimization, Springer series in operations research, 2nd edn. Springer, Berlin

    Google Scholar 

  27. Sivasubramani S, Swarup KS (2011) Sequential quadratic programming based differential evolution algorithm for optimal power flow problem. IET Gener Transm Distrib 5(11):1149–1154

    Article  Google Scholar 

  28. Aleem SHEA, Zobaa AF, Abdel Aziz MM (2012) Optimal C-type passive filter based on minimization of the voltage harmonic distortion for nonlinear loads. IEEE Trans Indu Electron 59(1):281–289

    Article  Google Scholar 

  29. Jiejin C, Qiong L, Lixiang L, Haipeng P, Yixian Y (2012) A hybrid FCASO-SQP method for solving the economic dispatch problems with valve-point effects. Energy 38(1):346–353

    Article  Google Scholar 

  30. Yu MT, Lin TY, Hung C (2012) Sequential quadratic programming method with a global search strategy on the cutting-stock problem with rotatable polygons. J Intell Manuf 23(3):787–795

    Article  Google Scholar 

  31. Izmailov AF, Pogosyan AL A semismooth sequential quadratic programming method for lifted mathematical programs with vanishing constraints. Comput Math Math Phys 51.6 (2011): 919–941

  32. Tang C, et al (2013) A feasible SQP-GS algorithm for nonconvex, nonsmooth constrained optimization. Numer Algorithms (2013): 1–22

  33. Syam MI, Hamdan A (2006) An efficient method for solving Bratu equations. Appl Math Comput 176:704–713

    Article  MATH  MathSciNet  Google Scholar 

  34. Muhammed Syam I (2007) The modified Broyden-variational method for solving nonlinear elliptic differential equations. Chaos Solitons Fract 32:392–404

    Article  MATH  Google Scholar 

  35. Gidas B, Ni W, Nirenberg L (1979) Symmetry and related properties via the maximum principle. Comm Math Phys 68:209–243

    Article  MATH  MathSciNet  Google Scholar 

  36. Bratu G (1914) Sur les équations intégrales non linéaires. Bull Soc Math France 43:113–142

    MathSciNet  Google Scholar 

  37. Gelfand IM (1963) Some problems in the theory of quasi-linear equations. Trans Am Math Soc Ser 2:295–381

    Google Scholar 

  38. Jacobsen J, Schmitt K (2002) The Liouville-Bratu-Gelfand problem for radial operators. J Diff Eq 184:283–298

    Article  MATH  MathSciNet  Google Scholar 

  39. Buckmire R (2003) On exact and numerical solutions of the one-dimensional planar Bratu problem, 2003. http://faculty.oxy.edu/ron/research/bratu/bratu.pdf

  40. Frank-Kamenetski DA (1955) Diffusion and heat exchange in chemical kinetics. Princeton University Press, Princeton

    Google Scholar 

  41. Wan YQ, Guo Q, Pan N (2004) Thermo-electro-hydrodynamic model for electrospinning process. Int J Nonlinear Sci Numer Simul 5(1):5–8

    Article  Google Scholar 

  42. Beidokhti RS, Malek A (2009) Solving initial-boundary value problems for systems of partial differential equations using neural networks and optimization techniques. J Franklin Inst 346(9):898–913

    Article  MathSciNet  Google Scholar 

  43. Parisi DR, Mariani MC, Laborde MA (2003) Solving differential equations with unsupervised neural networks. Chem Eng Process 42(8–9):715–721

    Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Electrical Engineering, COMSATS Institute of Information Technology, Attock, Pakistan

    Muhammad Asif Zahoor Raja

  2. Mohammad Ali Jinnah University, Islamabad, Pakistan

    Raza Samar

  3. Mechanical Engineering Department, University of Michigan-Shanghai Jiao Tong University Joint Institute, Shanghai Jiao Tong University, Shanghai, Peoples Republic of China

    Mohammad Mehdi Rashidi

  4. Mechanical Engineering Department, Engineering Faculty of Bu-Ali Sina University, Hamedan, Iran

    Mohammad Mehdi Rashidi

Authors
  1. Muhammad Asif Zahoor Raja
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Raza Samar
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Mohammad Mehdi Rashidi
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Muhammad Asif Zahoor Raja.

Appendix

Appendix

The derived solutions by each neural networks model in case of all three BVPs of Bratu-type equations are given in Tables 8, 9 and 10, respectively. The solutions are presented with 14 decimal points for the unknown weights to exactly reproduce the results presented in the body of manuscript and to avoid rounding of error problem.

Table 8 Derive solutions by neural network models in case of problem 1
Full size table
Table 9 Derive solutions by neural network models in case of problem 2
Full size table
Table 10 Derive solutions by neural network models in case of Problem 3
Full size table

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Raja, M.A.Z., Samar, R. & Rashidi, M.M. Application of three unsupervised neural network models to singular nonlinear BVP of transformed 2D Bratu equation. Neural Comput & Applic 25, 1585–1601 (2014). https://doi.org/10.1007/s00521-014-1641-x

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00521-014-1641-x

Keywords

Search

Navigation