Skip to main content
SpringerLink
Log in

A cubic q-rung orthopair fuzzy TODIM method based on Minkowski-type distance measures and entropy weight

  • Soft computing in decision making and in modeling in economics
  • Published:
Soft Computing Aims and scope Submit manuscript

Abstract

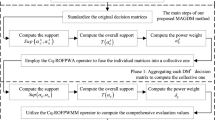
The main aim of the present study is to develop a novel TODIM method under cubic q-rung orthopair fuzzy environment, where information about the weights of both decision makers (DMs) and criteria is fully unknown. First, we introduce some novel operations along with their relevant properties. Afterward, we propose a Minkowski-type distance measure for cubic q-rung orthopair fuzzy sets (Cq-ROFSs). We list some properties of the proposed distance measures and some special cases about various parameter values. Next, the entropy measure between two Cq-ROFSs is disclosed, and part of the proposed entropy measure characteristics is presented. Further, this study put forward the method for finding the weights of DMs and criteria. In the developed method, firstly, weights of DMs are obtained using the proposed distance measure and cubic q-rung orthopair fuzzy weighted averaging operator. Then, the weights of criteria are determined by the developed entropy measure. A novel TODIM method is developed utilizing the proposed Minkowski-type distance measures for ranking alternatives in light of the acquired criteria weights. To demonstrate the applicability and validity of the presented work, we address the talent recruitment problem. Moreover, we discuss the influence of parameters on decision-making results. Finally, a comparative study with existing work is made.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5

Similar content being viewed by others

Data availability

Enquiries about data availability should be directed to the authors.

References

  • Ali J (2021) A novel score function based CRITIC-MARCOS method with spherical fuzzy information. Comput Appl Math 40(8):280

    MathSciNet  MATH  Google Scholar 

  • Ali J (2022) A q-rung orthopair fuzzy MARCOS method using novel score function and its application to solid waste management. Appl Intell 52(8):8770–8792

    MathSciNet  Google Scholar 

  • Ali J, Garg H (2023) On spherical fuzzy distance measure and TAOV method for decision-making problems with incomplete weight information. Eng Appl Artif Intell 119:105726

    Google Scholar 

  • Ali J, Bashir Z, Rashid T (2021a) Weighted interval-valued dual-hesitant fuzzy sets and its application in teaching quality assessment. Soft Comput 25(5):3503–3530

  • Ali J, Bashir Z, Rashid T (2021b) On distance measure and TOPSIS model for probabilistic interval-valued hesitant fuzzy sets: application to healthcare facilities in public hospitals. Grey Syst Theory Appl 12(1):197–229

  • Ali J, Bashir Z, Rashid T (2021c) WASPAS-based decision making methodology with unknown weight information under uncertain evaluations. Expert Syst Appl 168:114143

  • Ali J, Bashir Z, Rashid T (2022) A multi-criteria group decision-making approach based on revised distance measures under dual hesitant fuzzy setting with unknown weight information. Soft Comput 26(17):8387–8401

    Google Scholar 

  • Atanassov KT (1986) Intuitionistic fuzzy sets. Fuzzy Sets Syst 20(1):87–96

    MathSciNet  MATH  Google Scholar 

  • Biswas A, Sarkar B (2019) Pythagorean fuzzy TOPSIS for multicriteria group decision-making with unknown weight information through entropy measure. Int J Intell Syst 34(6):1108–1128

    Google Scholar 

  • Chen L, Luo N, Gou X (2021) A novel q-rung orthopair fuzzy TODIM approach for multi-criteria group decision making based on Shapley value and relative entropy. J Intell Fuzzy Syst 40(1):235–250

    Google Scholar 

  • Du WS (2018) Minkowski-type distance measures for generalized orthopair fuzzy sets. Int J Intell Syst 33(4):802–817

    Google Scholar 

  • Fan Z-P, Zhang X, Chen F-D, Liu Y (2013) Extended TODIM method for hybrid multiple attribute decision making problems. Knowl Based Syst 42:40–48

    Google Scholar 

  • Farhadinia B, Effati S, Chiclana F (2021) A family of similarity measures for q-rung orthopair fuzzy sets and their applications to multiple criteria decision making. Int J Intell Syst 36(4):1535–1559

    Google Scholar 

  • Gao H, Ran L, Wei G, Wei C, Wu J (2020) VIKOR method for MAGDM based on q-rung interval-valued orthopair fuzzy information and its application to supplier selection of medical consumption products. Int J Environ Res 17(2):525

    Google Scholar 

  • Garg H (2017) Generalized pythagorean fuzzy geometric aggregation operators using Einstein t-norm and t-conorm for multicriteria decision-making process. Int J Intell Syst 32(6):597–630

    Google Scholar 

  • Garg H, Kumar K (2020) A novel exponential distance and its based TOPSIS method for interval-valued intuitionistic fuzzy sets using connection number of SPA theory. Artif Intell Rev 53(1):595–624

    Google Scholar 

  • Gomes LFAM (2009) An application of the TODIM method to the multicriteria rental evaluation of residential properties. Eur J Oper Res 193(1):204–211

    MATH  Google Scholar 

  • Gomes L, Lima M (1991) TODIM: Basics and application to multicriteria ranking of projects with environmental impacts. Found Comput Decis Sci 16(4):113–127

    MATH  Google Scholar 

  • Gomes L, Lima M (1992) From modeling individual preferences to multicriteria ranking of discrete alternatives: a look at prospect theory and the additive difference model. Found Comput Decis Sci 17(3):171–184

    MATH  Google Scholar 

  • Gou X, Xu Z (2017) Exponential operations for intuitionistic fuzzy numbers and interval numbers in multi-attribute decision making. Fuzzy Optim Decis Making 16(2):183–204

    MathSciNet  MATH  Google Scholar 

  • Grabisch M (1995) A new algorithm for identifying fuzzy measures and its application to pattern recognition. In: Proceedings of 1995 IEEE international conference on fuzzy systems, vol. 1. IEEE, pp 145–150

  • Ji P, Zhang H-Y, Wang J-Q (2018) A projection-based TODIM method under multi-valued neutrosophic environments and its application in personnel selection. Neural Comput Appl 29(1):221–234

    Google Scholar 

  • Jiang Q, Jin X, Lee S-J, Yao S (2019) A new similarity/distance measure between intuitionistic fuzzy sets based on the transformed isosceles triangles and its applications to pattern recognition. Expert Syst Appl 116:439–453

    Google Scholar 

  • Joshi BP, Singh A, Bhatt PK, Vaisla KS (2018) Interval valued q-rung orthopair fuzzy sets and their properties. J Intell Fuzzy Syst 35(5):5225–5230

    Google Scholar 

  • Kahneman D, Tversky A (2013) Chapter 6, Prospect theory: an analysis of decision under risk. In: Handbook of the fundamentals of financial decision making, pp 99–127. https://doi.org/10.1142/9789814417358_0006

  • Kumar K, Garg H (2018) TOPSIS method based on the connection number of set pair analysis under interval-valued intuitionistic fuzzy set environment. Comput Appl Math 37(2):1319–1329

    MathSciNet  MATH  Google Scholar 

  • Leoneti AB, Gomes LFAM (2021) A novel version of the TODIM method based on the exponential model of prospect theory: the ExpTODIM method. Eur J Oper Res 295(3):1042–1055

    MathSciNet  MATH  Google Scholar 

  • Lin M, Wang H, Xu Z (2019) TODIM-based multi-criteria decision-making method with hesitant fuzzy linguistic term sets. Artif Intell Rev 53:3647–3671

    Google Scholar 

  • Liu P, Liu J, Chen S-M (2018) Some intuitionistic fuzzy Dombi Bonferroni mean operators and their application to multi-attribute group decision making. J Oper Res Soc 69(1):1–24

    Google Scholar 

  • Mahmoodzadeh S, Shahrabi J, Pariazar M, Zaeri M (2007) Project selection by using fuzzy AHP and TOPSIS technique. World Acad Sci Eng Technol 30:333–338

    Google Scholar 

  • Mahnaz S, Ali J, Malik MGA, Bashir Z (2021) T-spherical fuzzy Frank aggregation operators and their application to decision making with unknown weight information. IEEE Access 10:7408–7438

    Google Scholar 

  • Malik M, Bashir Z, Rashid T, Ali J (2018) Probabilistic hesitant intuitionistic linguistic term sets in multi-attribute group decision making. Symmetry 10(9):392

    MATH  Google Scholar 

  • Peng X, Yang Y (2015) Some results for pythagorean fuzzy sets. Int J Intell Syst 30(11):1133–1160

    MathSciNet  Google Scholar 

  • Pramanik S, Dalapati S, Alam S, Smarandache F, Roy TK (2018) NS-cross entropy-based MAGDM under single-valued neutrosophic set environment. Information 9(2):37

    Google Scholar 

  • Roy J, Das S, Kar S, Pamučar D (2019) An extension of the CODAS approach using interval-valued intuitionistic fuzzy set for sustainable material selection in construction projects with incomplete weight information. Symmetry 11(3):393

    Google Scholar 

  • Seker S, Kahraman C (2022) A Pythagorean cubic fuzzy methodology based on TOPSIS and TODIM methods and its application to software selection problem. Soft Comput 14(3):2437–2450

    Google Scholar 

  • Shannon CE (2001) A mathematical theory of communication. Mobile Comput Commun Rev 5(1):3–55

    MathSciNet  Google Scholar 

  • Shao Y, Qi X, Gong Z (2020) A general framework for multi-granulation rough decision-making method under q-rung dual hesitant fuzzy environment. Artif Intell Rev 53:4903–4933

    Google Scholar 

  • Verma R (2020) Multiple attribute group decision-making based on order-\(\alpha \) divergence and entropy measures under q-rung orthopair fuzzy environment. Int J Intell Syst 35(4):718–750

    Google Scholar 

  • Wang L, Garg H (2021) Algorithm for Multiple Attribute Decision-Making with Interactive Archimedean Norm Operations Under Pythagorean Fuzzy Uncertainty. Int J Comput Intell Syst 14(1):503–527

    Google Scholar 

  • Wang X, Triantaphyllou E (2008) Ranking irregularities when evaluating alternatives by using some ELECTRE methods. Omega 36(1):45–63

    Google Scholar 

  • Wang F, Zhao X (2021) Prospect-theory and geometric distance measure-based Pythagorean cubic fuzzy multicriteria decision-making. Int J Intell Syst 36:4117–4142

    Google Scholar 

  • Wang J, Wei G, Lu M (2018) TODIM method for multiple attribute group decision making under 2-tuple linguistic neutrosophic environment. Symmetry 10(10):486

    Google Scholar 

  • Wang J, Gao H, Wei G, Wei Y (2019) Methods for multiple-attribute group decision making with q-rung interval-valued orthopair fuzzy information and their applications to the selection of green suppliers. Symmetry 11(1):56

    MATH  Google Scholar 

  • Wang J, Shang X, Bai K, Xu Y (2020) A new approach to cubic q-rung orthopair fuzzy multiple attribute group decision-making based on power Muirhead mean. Neural Comput Appl 32(17):14087–14112

    Google Scholar 

  • Wang L, Garg H, Li N (2021) Pythagorean fuzzy interactive Hamacher power aggregation operators for assessment of express service quality with entropy weight. Soft Comput 25(2):973–993

    MATH  Google Scholar 

  • Wei G (2018) TODIM method for picture fuzzy multiple attribute decision making. Informatica 29(3):555–566

    MathSciNet  MATH  Google Scholar 

  • Wei C-P, Wang P, Zhang Y-Z (2011) Entropy, similarity measure of interval-valued intuitionistic fuzzy sets and their applications. Inf Sci 181(19):4273–4286

    MathSciNet  MATH  Google Scholar 

  • Wei C, Ren Z, Rodríguez RM (2015) A hesitant fuzzy linguistic TODIM method based on a score function. Int J Comput Intell Syst 8(4):701–712

    Google Scholar 

  • Xu X-H, Luo X (2019) Information entropy risk measure applied to large group decision-making method. Soft Comput 23(13):4987–4997

    Google Scholar 

  • Xu Y, Shang X, Wang J, Wu W, Huang H (2018) Some q-rung dual hesitant fuzzy heronian mean operators with their application to multiple attribute group decision-making. Symmetry 10(10):472

    Google Scholar 

  • Yager RR (2013) Pythagorean membership grades in multicriteria decision making. IEEE Trans Fuzzy Syst 22(4):958–965

    Google Scholar 

  • Yager RR (2016) Generalized orthopair fuzzy sets. IEEE Trans Fuzzy Syst 25(5):1222–1230

    Google Scholar 

  • Ye J (2010) Fuzzy decision-making method based on the weighted correlation coefficient under intuitionistic fuzzy environment. Eur J Oper Res 205(1):202–204

    MATH  Google Scholar 

  • Zadeh LA (1965) Fuzzy sets. Inf Control 8(3):338–353

    MATH  Google Scholar 

  • Zhang Q, Xing H, Liu F, Ye J, Tang P (2014) Some new entropy measures for interval-valued intuitionistic fuzzy sets based on distances and their relationships with similarity and inclusion measures. Inf Sci 283:55–69

  • Zhang F, Chen S, Li J, Huang W (2018) New distance measures on hesitant fuzzy sets based on the cardinality theory and their application in pattern recognition. Soft Comput 22(4):1237–1245

  • Zindani D, Maity SR, Bhowmik S (2020) Interval-valued intuitionistic fuzzy TODIM method based on Schweizer–Sklar power aggregation operators and their applications to group decision making. Soft Comput 24:14091–14133

    Google Scholar 

Download references

Funding

The authors have not disclosed any funding.

Author information

Authors and Affiliations

  1. Institute of Numerical Sciences, Kohat University of Science and Technology, Kohat, KPK, 26000, Pakistan

    Jawad Ali

  2. Department of Mathematics, Quaid-i-Azam University, Islamabad, 45320, Pakistan

    Zia Bashir

  3. Department of Mathematics, University of Management and Technology, Lahore, 54770, Pakistan

    Tabasam Rashid

Authors
  1. Jawad Ali
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Zia Bashir
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Tabasam Rashid
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Tabasam Rashid.

Ethics declarations

Conflict of interest

The authors have not disclosed any competing interests.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Ali, J., Bashir, Z. & Rashid, T. A cubic q-rung orthopair fuzzy TODIM method based on Minkowski-type distance measures and entropy weight. Soft Comput 27, 15199–15223 (2023). https://doi.org/10.1007/s00500-023-08552-8

Download citation

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00500-023-08552-8

Keywords

Search

Navigation