Wind speed forecast based on combined theory, multi-objective optimisation, and sub-model selection

Abstract

Wind energy is the primary energy source for a sustainable and pollution-free global power supply. However, because of its characteristic irregularity, nonlinearity, non-stationarity, randomness, and intermittency, previous studies have only focused on stability or accuracy, and the forecast performances of their models were poor. Moreover, in previous research, the selection of sub-models used for the combined model was not considered, which weakened the generalisability. Therefore, to further improve the forecast accuracy and stability of the wind speed forecasting model, and to solve the problem of sub-model selection in the combined model, this study developed a wind speed forecasting model using data pre-processing, a multi-objective optimisation algorithm, and sub-model selection for the combined model. Simulation experiments showed that our combined model not only improved the forecasting accuracy and stability but also chose different sub-models and different weights of the combined model for different data; this improved the model generalisability. Specifically, the MAPEs of our model are less than 4.96%, 4.60%, and 5.25% in one-, two-, and three-step forecast. Thus, the proposed combined model is demonstrated as an effective tool for grid dispatching.

Appendix

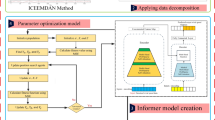
For the data, only with a better understanding of the features of the data we can better select the model to prepare for future work. In order to achieve better results, we must consider the characteristics of the data. Generally speaking, the linear model has a better fitting effect for linear data, as the nonlinear model does for nonlinear data.

Only when we understand the characteristics of the data we can achieve good results in future forecasting work. For the data, it is not just linear or nonlinear, but both. Therefore, it is necessary to judge the linear nonlinearity of the data used in this paper, so we constructed the above experiments.

From the results of Tables 7 and 8, wind speed data are both linear and nonlinear by hypothesis test. So, the linear models and nonlinear models considered in our proposed forecasting model are correct and necessary.

Table 7 Testing wind speed data by adjusting to linear functions or nonlinear functions

Table 8 The explanations of the test parameters

1.1 Basic methods and theories

1.1.1 Support vector machines

The support vector machine (SVM) method is a machine learning method that was proposed by Vapnik (1997) and the nonlinear function can be written as follows:

$$ f \left( x \right) = \omega^{T} \phi \left( x \right) + b $$

(8)

where $\phi \left( x \right)$ is the kernel function that maps the data from low-dimensional space to high dimensional space. ${\upomega }$ and b are the coefficient and threshold, respectively.

Using loss function $\varepsilon$ to optimize regression function, and the best regression function is found by the minimum value of the loss function. $\varepsilon$ is as follows:

$$ \varepsilon = \min \frac{1}{2}\omega^{T} \omega + C\mathop \sum \limits_{i = 1}^{n} \left( {\xi_{i} + \hat{\xi }_{i} } \right) $$

(9)

Constraints:

$$ \left\{ {\begin{array}{*{20}l} {y_{i} - \left[ {\omega , \phi \left( {x_{i} } \right)} \right] - b \le \xi_{i} + \varepsilon } \hfill \\ {\left[ {\omega , \phi \left( {x_{i} } \right)} \right] + b - y_{i} \le \hat{\xi }_{i} + \varepsilon } \hfill \\ {\xi_{i} \ge 0,\hat{\xi }_{i} \ge 0 } \hfill \\ \end{array} } \right. $$

(10)

where C is a penalty factor: $\xi_{i}$, $\hat{\xi }_{i}$ are slack variables, b is the offset, and $x_{i}$, $y_{i}$ are the input and output, respectively.

After the operation, the linear regression function can be obtained as follows:

$$ f\left( x \right) = \mathop \sum \limits_{i = 1}^{n} \left( {\beta_{i} - \alpha_{i} } \right)K\left( {x_{g} x_{i} } \right) + b $$

(11)

where $K\left( {x_{g} x_{i} } \right)$ is the kernel function of SVM.

1.1.2 Long short-term memory network

The long short-term memory (LSTM) network is a recurrent neural network (RNN), which was proposed by Hochreiter and Schmidhuber (Hochreiter and Schmidhuber 1997) in 1997 and can be written as follows (Greff et al. 2017):

$$ z^{t} = g(\omega_{z} x^{t} + r_{z} y^{t - 1} + b_{z} ) $$

(12)

$$ i^{t} = \sigma (\omega_{i} x^{t} + r_{i} y^{t - 1} + p_{i} c^{t - 1} + b_{i} ) $$

(13)

$$ f ^{t} = \sigma (\omega_{f} x^{t} + r_{f} y^{t - 1} + p_{f} c^{t - 1} + b_{f} ) $$

(14)

$$ c^{t} = z^{t} i^{t} + c^{t - 1} f^{t} $$

(15)

$$ o^{t} = \sigma (\omega_{o} x^{t} + r_{o} y^{t - 1} + p_{o} c^{t} + b_{o} ) $$

(16)

$$ y^{t} = h(c^{t} )o^{t} $$

(17)

$$ \sigma \left( x \right) = \frac{1}{{1 + e^{ - x} }} $$

(18)

$$ g\left( x \right) = h\left( x \right) = \tanh (x) $$

(19)

where t is the time; N is the cells of LSTM; $\omega_{z} , \omega_{i} , \omega_{f} , \omega_{o} \in R^{N \times M}$ are the input weights; $r_{z} , r_{i} , r_{f} , r_{o} \in R^{N \times M}$ are the recurrent weights; $p_{i} , p_{f} , p_{o} \in R^{N}$ are the peephole weights (Gers and Schmidhuber 2000); $b_{z} , b_{i} , b_{f} , b_{o} \in R^{N}$ are the biases; $g\left( x \right), h\left( x \right)$ and $\sigma \left( x \right)$ are activation functions; $z^{t}$ is the activation of the input block; $i^{t}$ is the activation of the input gate; $f ^{t}$ is the activation of the forget gate; $c^{t}$ is the cell state at time t; $o^{t}$ is the activation of the output gate; and $y^{t}$ is the output of the cell at time t.

1.1.3 Autoregressive integrated moving average

The autoregressive integrated moving average (ARIMA) model is one of the most popular forecasting models in the wind speed forecasting field (Contreras et al. 2003) and can be written as follows:

$$ \phi \left( B \right)\left( {1 - B} \right)^{d} X_{t} = \theta (B)\varepsilon_{t} $$

(20)

$$ \phi \left( B \right) = 1 - \phi_{1} B - \phi_{2} B^{2} - \cdots \phi_{P} B^{P} $$

(21)

$$ \theta \left( B \right) = 1 - \theta_{1} B - \theta_{2} B^{2} - \cdots - \theta_{q} B^{q} $$

(22)

These above formulas are recorded as ARIMA (p, d, q), where $B^{q} X_{t} = X_{t - q}$, $X_{t}$ is a time series at time t, $\varepsilon_{t}$ is the random error at time t, and B is the backward shift operator.

1.1.4 Back-propagation neural network

Back-propagation neural network (BPNN) is a widely used multi-layer feedforward neural network that is based on a gradient descent method that minimizes the sum of the squared errors between the actual output value and the expected output value. The output function is between 0 and 1, which can convert input to output to achieve continuous non-linear mapping (Guo et al. 2011) and can be written as follows:

The topology of the BPNN is as follows:

$$ X^{\prime } = \left\{ {X_{i}^{\prime } } \right\} = 2\frac{{X_{i} - X_{i\min } }}{{X_{i\max } - X_{i\min } }} - 1, \left( {i = 1, 2, \ldots , n} \right), X^{\prime } \subset [ - 1, 1] $$

(23)

where X_min and X_max are the minimum and maximum value of the input array or output vectors, and $X_{i}^{{\prime }}$ denotes the real value of each vector.

Step 1. Calculate the outputs of all hidden layer nodes:

$$ y_{j} = f (\mathop \sum \limits_{i} w_{ji} x_{i} + b_{j} ) = f({\text{net}}_{j} ) (i = 1, \ldots , n; j = 1, \ldots , 2n) $$

(24)

$$ {\text{net}}_{j} = \mathop \sum \limits_{i} w_{ji} x_{i} + b_{j} , ( j = 1, \ldots , 2n) $$

(25)

where the activation value of node j is ${\text{net}}_{j}$, $w_{ji}$ represents the connection weight from input node i to hidden node j, b_j represents the bias of neuron j, y_j represents the output of hidden layer node j, and f is the activation function of a node, which is usually a sigmoid function.

Step 2. Calculate the output data of the neural network:

$$ O_{1} = f_{0} \left( {\mathop \sum \limits_{j} w_{0j} y_{i} + b_{0} } \right), (i = 1, \ldots , 2n) $$

(26)

where $w_{0j}$ represents the connection threshold from hidden node j to the output node, b₀ represents the bias of the neuron, O₁ represents the output data of the network, and f₀ is the activation function of the output layer node.

Step 3. Minimize the global error via the training algorithm:

$$ {\text{Mean}}\,{\text{Square}}\,{\text{Error}} = \frac{1}{m}\sum (O_{1} - Z)^{2} $$

(27)

where Z represents the real data vector of the output, and m represents the number of outputs.

1.1.5 Generalized regression neural network

Generalized regression neural networks (GRNN) were proposed by Specht (1991), and the theoretical basis was nonlinear kernel regression analysis. The network was based on nonlinear regression theory and consisted of four layers of neurons: the input layer, pattern layer, summation layer, and output layer.

Definition 1

Setting the joint probability density function of the random variable x and y to f (x, y), the observed value of x is X. Thus, the estimation value as follows:

$$ \hat{Y} = E\left[ {\left. y \right|X} \right] = \mathop \int \limits_{ - \infty }^{ + \infty } xf (X, y){\text{d}}y/\mathop \int \limits_{ - \infty }^{ + \infty } f (X, y){\text{d}}y $$

(28)

Definition 2

To set the probability density function f (x, y), which is unknown, but can be obtained using a nonparametric estimation, we use the sample observation values of x and y:

$$ \hat{f} (x, y) = \frac{1}{{n\delta^{p + 1} (2\pi )^{(p + 1)/2} }}\mathop \sum \limits_{t = 1}^{n} \exp \left[ { - \frac{{(X - X_{t} )^{T} (X - X_{t} )}}{{2\delta^{2} }}} \right]\exp \left[ { - \frac{{(Y - Y_{t} )}}{{2\delta^{2} }}} \right] $$

(29)

where X_t and Y_t are the sample observation values of x and y, respectively; $\delta$ is the smoothing parameter; n is the number of samples; and p is the dimensionality of the random vector x. Here, we can calculate Y using f (x, y) instead of f (x, y) in formula (30). Finally,

$$ \hat{Y}(X) = \mathop \sum \limits_{t = 1}^{n} Y_{t} \exp \left[ { - \frac{{(X - X_{t} )^{T} (X - X_{t} )}}{{2\delta^{2} }}} \right]/\mathop \sum \limits_{t = 1}^{n} \exp \left[ { - \frac{{(X - X_{t} )^{T} (X - X_{t} )}}{{2\delta^{2} }}} \right] $$

(30)

where $\hat{Y}(X)$ is the weighted average of all sample observations of $Y_{t}$, and every weight factor $Y_{t}$ is the Euclidean squared distance index value between the corresponding samples $X_{t}$ and X.

1.1.6 Radial basis function neural network

The radial basis function neural network (RBFNN) (Schwenker et al. 2001) is an efficient feedforward neural network that exhibits better approximation performance and global optimal ability than other feedforward networks. The structure of the neural network is simple and the training speed is fast. An RBFNN also includes three layers: an input layer, a hidden layer with a nonlinear activation function (the radial basis function), and an output layer.

The RBFNN was proposed by Schwenker, and this network exhibits better approximation performance and global optimal ability than other feedforward networks. The neural network also has a simple structure and fast training speed. There are three layers: an input layer, an output layer, and a hidden layer with a nonlinear activation function.

Definition 1

The modelled input is a real-number vector $x \in {\mathbb{R}}^{n}$. Then, the output vector of the neural network is a scalar function of the input vector, $\varphi :{\mathbb{R}}^{n} \to {\mathbb{R}}$, given by

$$ \varphi (x) = \mathop \sum \limits_{i = 1}^{N} a_{i} \rho (\left\| {x - c_{i} } \right\|), $$

(31)

where N represents the total number of neurons in the hidden layer, the centre vector of the ith neuron is represented by ${\text{c}}_{{\text{i}}}$, and ${\text{a}}_{{\text{i}}}$ is the weight of neuron i in the linear output neuron.

Definition 2

A radial basis function is a scalar function that is radially symmetric. Thus, it is defined as a monotone function of the Euclidean distance between any point x in space and $c_{i}$ of a centre vector. The most commonly used radial basis function is the Gauss kernel function, given as follows:

$$ k(x - c_{i} ) = \exp \left\{ {\frac{{\left\| {x - c_{i} } \right\|^{2} }}{{\left( {2\sigma } \right)^{2} }}} \right\} $$

(32)

where $c_{i}$ is a centre vector and $\sigma$ is a width parameter that controls the radial scope of the function.

1.1.7 Adaptive network-based fuzzy inference system

Jang (1993) combined the best features of the fuzzy system and neural network to construct an adaptive network-based fuzzy inference system (ANFIS). ANFIS integrates the human inference style of fuzzy inference system (FIS) by using input–output sets and a set of if–then fuzzy rules. FIS (Neshat et al. 2012) has structured knowledge, in which each fuzzy rule describes the current behaviour of the system; however, it lacks adaptability to changes in the external environment. Therefore, the concept of neural network learning and FIS are combined in ANFIS (İnan et al. 2007). ANFIS is a method that uses neural network learning and fuzzy inference to simulate complex nonlinear mapping. This method has the ability to deal with the uncertain noisy and imprecise environments (Liu and Ling 2003). ANFIS uses the training process of the neural network to adjust the membership function and the related parameters close to the expected data set (Wu et al. 2009).

Layer 1: This layer is the input layer, which is responsible for the fuzziness of the input signal. Each node I is a node function represented by square node:

$$ O_{i}^{1} = \mu_{{A_{i} }} \left( x \right), i = 1,2\quad {\text{or}}\quad O_{i}^{1} = \mu_{{B_{i} }} \left( y \right), i = 1,2 $$

(33)

where x (or y) is the input of node i, A_i, B_i are fuzzy sets, and $O_{i}^{1}$ is the membership function value of A_i and B_i, indicating the degree to which X and Y belong to A_i and B_i. Usually, the $\mu_{{A_{i} }}$ and $\mu_{{B_{i} }}$ are chosen as bell-shaped functions or Gaussian functions. The membership function has some parameters; these parameters are called premise parameters.

Layer 2: The nodes in this layer are responsible for multiplying the input signals and calculating the firing strength of each rule. The output is

$$ O_{i}^{2} = \omega_{i} = \mu_{{A_{i} }} \left( x \right) \times \mu_{{B_{i} }} \left( y \right), i = 1,2 $$

(34)

where the output of each node represents the credibility of the rule.

Layer 3: This layer normalizes all applicability, each node is represented by N. The ratio of the ith rule’s firing strengths to the sum of all rules’ firing strengths is calculated by the ith node:

$$ O_{i}^{3} = \overline{\omega }_{i} = \omega_{i} /\left( {\omega_{1} + \omega_{2} } \right) i = 1,2. $$

(35)

Layer 4: Calculating the output of the fuzzy rule, the output is

$$ O_{i}^{4} = \overline{\omega }_{i} f_{i} = (p_{i} x + q_{i} y + r_{i} ) i = 1,2 $$

(36)

where $\overline{\omega }_{i}$ is the output of layer 3 and {p_i, q_i, r_i} is the parameter set (consequent parameters).

Layer 5: The single node of this layer is a fixed node that calculates the total output of all input signals:

$$ O_{i}^{5} = \mathop \sum \limits_{i} \overline{\omega }_{i} f_{i} . $$

(37)

1.1.8 Extreme learning machine

Extreme learning machine (ELM) is a machine learning algorithm proposed by Huang, which was designed for single-layer feedforward neural networks (SLFNNs) (Huang et al. 2006). The main feature of ELM is that the parameters of hidden layer nodes can be randomly generated without adjustment. The learning process only needs to calculate the output weights.

Definition 3

An SLFNN consists of three parts: an input layer, hidden layer, and output layer. The output function of the hidden layer is given as follows:

$$ f_{L} = \mathop \sum \limits_{i = 1}^{l} \beta_{i} h_{i} (x) = h(x) \beta , $$

(38)

where x is the input vector, $\beta$ is the output weight of the ith hidden node, and h(x) is the hidden layer output mapping, called the activation function, defined as follows:

$$ h(x) = G(a_{i} , b_{i} , x). $$

(39)

Here, $b_{i}$ is the parameter of the feature mapping (also called the node parameter), and $a_{i}$ is called the input weight. In the calculation, the parameter of the feature mapping is randomly initialized and is not adjusted. Hence, the feature mapping of the ELM is also random.

1.1.9 Elman neural network

The Elman neural network is a machine learning algorithm proposed by Elman designed for SLFNN. In addition to the input layer, the hidden layer, and the output layer, it also has a special contact unit. The contact unit is used to memorize the previous output value of the hidden layer unit. It can be considered as a delay operator. Therefore, the feedforward link part can be corrected for the connection weight, whilst the recursive part is fixed, that is, the learning correction cannot be performed. The mathematic model of Elman can be written as follows (Elman 1990):

$$ x\left( k \right) = f (W^{ I1} x_{c} \left( k \right) + (W^{ I2} u\left( {k - 1} \right)) $$

(40)

$$ x_{c} \left( k \right) = \alpha x_{c} \left( {k - 1} \right) + x (k - 1) $$

(41)

$$ y\left( k \right) = W^{ I3} x(k) $$

(42)

where f (x) is a sigmoid function, and $0 \le \alpha < 1$ is a self-connected feedback gain operator. If the $\alpha = 0$, then the network is a standard Elman neural network, if the $\alpha \ne 0$, then the network is a modified Elman neural network, u is the input data with n-dimensional vector, x is a hidden layer output, X_c is the hidden layer output with an n-dimensional vector, y is the output for the network with an m-dimensional vector, and W^I1, W^I2, and W^I3, are connection weights with $n \times n$-, $n \times q$-, and $m \times m$-dimensional matrices, respectively.

We set the actual output of the k-step system to be $y_{d} (k)$, define the error function as $E\left( k \right) = \frac{1}{2}(y_{d} (k) - y(k))^{T} (y_{d} (k) - y(k))$, and let derivative E be the connection weights A, W^I1, W^I2, W^I3. The learning algorithm of an Elman network can be obtained using the gradient descent method:

$$ \Delta w_{ij}^{I3} = \eta_{3} \delta_{i}^{0} x_{j} \left( k \right), i = 1, 2, \ldots , m; j = 1, 2, \ldots , n $$

(43)

$$ \Delta w_{jq}^{I2} = \eta_{2} \delta_{j}^{h} u_{q} \left( {k - 1} \right), j = 1, 2, \ldots , n; q = 1, 2, \ldots , r $$

(44)

$$ \Delta w_{jl}^{I1} = \eta_{1} \mathop \sum \limits_{i = 1}^{m} (\delta_{i}^{0} w_{ij}^{I3} )\frac{{\partial x_{j} (k)}}{{\partial w_{jl}^{I1} }}, j = 1, 2, \ldots , n; l = 1, 2, \ldots , n $$

(45)

where r is the node number of the input layer, n is the node number of the hidden layer and unit layer, and m is the node number of the output layer. $\eta_{1}$, $\eta_{2}$, and $\eta_{3}$ are the learning steps of $W^{I1}$, $W^{I2}$, and $W^{I3}$, respectively.

$$ \delta_{i}^{0} = (y_{d,i} \left( k \right) - y_{i} (k)) $$

(46)

$$ \delta_{j}^{h} = \mathop \sum \limits_{i = 1}^{m} (\delta_{i}^{0} w_{ij}^{I3} ) f_{j}^{\prime } ( \cdot ) $$

(47)

$$ \frac{{\partial x_{j} (k)}}{{\partial w_{jl}^{I1} }} = f_{j}^{{\prime }} ( \cdot )x_{l} \left( {k - 1} \right) + \alpha \frac{{\partial x_{j} (k - 1)}}{{\partial w_{jl}^{I1} }} $$

(48)

1.1.10 Weighted information criterion (WIC)

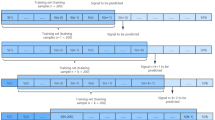
The weighted information criterion (WIC) was initially proposed to find the best ANN model (Egrioglu et al. 2008). In this paper, WIC was applied to four real-time series datasets in order to measure the forecasting performance of the examined sub-models’ architectures and to decide the sub-models of the combined model. The number of input nodes depends on the number of sub-models of the combined model. The mean absolute percentage error (MAPE), root mean square error (RMSE), Akaike information criterion (AIC), Bayesian information criterion (BIC), and direction accuracy (DA) were chosen as the model selection criteria. The MAPE and RMSE were used to detect deviations between the actual values and the forecasting values. The AIC and BIC were used for penalizing large models. The DA measured the forecasting direction accuracy. Although the MAPE and RMSE can also be used individually to select a model, the models they select tend not to be sufficiently detailed. These criteria are calculated as follows:

$$ {\text{MAPE}} = \frac{1}{T}\mathop \sum \limits_{i = 1}^{T} \left| {\frac{{y_{i} - \hat{y}_{i} }}{{y_{i} }}} \right| $$

(49)

$$ {\text{RMSE}} = \sqrt {\frac{1}{T}\mathop \sum \limits_{i = 1}^{T} \left( {y_{i} - \hat{y}_{i} } \right)^{2} } $$

(50)

$$ {\text{AIC}} = \log \left( {\frac{{\mathop \sum \nolimits_{i = 1}^{T} \left( {y_{i} - \hat{y}_{i} } \right)^{2} }}{T}} \right) + \frac{2m}{T} $$

(51)

$$ {\text{BIC}} = \log \left( {\frac{{\mathop \sum \nolimits_{i = 1}^{T} \left( {y_{i} - \hat{y}_{i} } \right)^{2} }}{T}} \right) + \frac{m\log (T)}{T} $$

(52)

$$ {\text{DA}} = \frac{1}{T}\mathop \sum \limits_{i = 1}^{T} a_{i} , a_{i} = \left\{ {\begin{array}{*{20}l} 1 \hfill & {if\quad \left( {y_{i + 1} - \hat{y}_{i} } \right)\left( {\hat{y}_{i + 1} - y_{i} } \right) > 0} \hfill \\ 0 \hfill & {\text{otherwise }} \hfill \\ \end{array} } \right. $$

(53)

where y is the actual value, $\hat{y}$ is the forecasted value, T is the total number of data items, and m is the number of ANN weights.

In this paper, we used a special criterion called the modified direction accuracy (MDA), which was proposed according to the special direction accuracy criterion. The MDA criterion is calculated in the following way:

$$ A_{j} = \left\{ {\begin{array}{*{20}l} 1 \hfill & {y_{j + 1} - y_{j} \le 0} \hfill \\ 0 \hfill & {y_{j + 1} - y_{j} > 0} \hfill \\ \end{array} } \right. $$

(54)

$$ F_{j} = \left\{ {\begin{array}{*{20}l} 1 \hfill & {\hat{y}_{j + 1} - \hat{y}_{j} \le 0} \hfill \\ 0 \hfill & {\hat{y}_{j + 1} - \hat{y}_{j} > 0} \hfill \\ \end{array} } \right. $$

(55)

$$ D_{j} = (A_{j} - F_{j} )^{2} $$

(56)

$$ {\text{MDA}} = \frac{{\mathop \sum \nolimits_{j = 1}^{T - 1} D_{j} }}{T - 1}. $$

(57)

The following describes the algorithm of model selection strategy based on WIC:

(1) All of the structure of the sub-models, which consist of the combined model are determined. For instance, we have five input layer nodes, one output layer node, and 15 hidden layer nodes. Thus, the total number of possible structures is 18.

(2) The best weights of AIC, BIC, RMSE, MAPE, DA, and MDA are determined using the training data and calculated with the training data.

(3) The five criteria must be standardized for neural network structures.

(4) Then, the WIC is calculated as follows:

WIC = 0.2 × (MAPE + RMSE) + 0.1 × (AIC + BIC) + 0.2 × (MDA + (1 – DA)).

(5) We choose an architecture with the minimum WIC.

1.1.11 The theory of the combined model

The combination forecasting theory indicates (Bates and Granger 2001) that if the M forecasting models can solve a certain forecasting problem, the weight coefficients should be appropriately selected, and then the results of the M forecasting methods are added to obtain a new model named the combined model. The results of the combined model are better than the M models. Assuming that the actual time series data is presented in the form of y, the number of sample points is i, y_i is the forecasting value obtained by the ith forecast model, the forecast error is e, and the weight coefficient of the ith forecasting model is w, then the general combined forecast model can be expressed as follows:

$$ y_{t} = \mathop \sum \limits_{i = 1}^{M} \omega_{i} \left( {\hat{y}_{it} + e_{it} } \right),\quad t = 1, 2, \ldots , L, $$

(58)

$$ \hat{y}_{t} = \mathop \sum \limits_{i = 1}^{M} \hat{\omega }_{i} \hat{y}_{it} ,\quad t = 1, 2, \ldots , L, $$

(59)

where $\hat{\omega }_{i}$ is the estimated value of $\omega_{i}$ and represents the weight of each single model, $\hat{y}_{t}$ is the forecasting value of the combined model. Determining the weight coefficient of each model is a key step in establishing a combined forecasting model. Then, by solving the optimization problem of the combination model, an optimal combination model can be obtained. Then this optimization problem can be expressed as:

$$ {\text{Min}}\mathop \sum \limits_{t = 1}^{L} \left| {y_{t} - \hat{y}_{t} } \right|, \quad {\text{s.t}}{. }\mathop \sum \limits_{i = 1}^{M} \omega_{i} = 1, 0 \le \omega_{i} \le 1, i = 1, 2, \ldots ,M. $$

(60)

When the predefined absolute error or the maximum number of iterations are reached, the optimization process is stopped.

1.1.12 Multi-objective optimization theory

The optimization problems of the objective function with multiple measurement indexes in the domain of definition can be solved by multi-objective optimizations. The objective function checks and balances the shortcomings of the forecast model in many aspects by assigning weights to each measurement index, to improve the forecasting accuracy and stability. Generally speaking, multi-objective optimization problems (MOPs) can be divided into two categories: constrained problems and non-constrained problems. A constrained problem with j inequality and k equality constraints can be expressed as (Laumanns et al. 2006):

$$ \begin{aligned} & {\text{Minimize}}\quad F\left( x \right) = \left( { f_{1} \left( x \right), f_{2} \left( x \right), \ldots , f_{M} \left( x \right) } \right)^{T} \\ & \quad {\text{s.t}}{.}\quad g_{j} \left( x \right) \ge 0, j = 1, 2, \ldots , J,\quad x \in \Omega \\ & \quad \quad h_{k} \left( x \right) = 0, k = 1,2, \ldots , K, \\ \end{aligned} $$

(61)

where M is the number of objectives, $x = (x_{1} , x_{2} , \ldots , x_{n} )^{T}$ is the decision vector, and n is the number of decision variables. In (61), $\Omega = \mathop \prod \nolimits_{i = 1}^{n} \left[ {x_{i}^{L} , x_{i}^{U} } \right] \subseteq R^{n}$ is called the decision space, where $x_{i}^{L}$ and $x_{i}^{U}$ are the lower and upper limits of the decision variables, respectively.

When the inequality and equality constraints in (61) are omitted, an unconstrained multi-objective problem is obtained, which is expressed as follows

$$ \begin{aligned} & {\text{Minimize}}\quad F\left( x \right) = \left( { f_{1} \left( x \right), f_{2} \left( x \right), \ldots , f_{M} \left( x \right) } \right)^{T} \\ & \quad {\text{s.t}}{.}\quad x \in \Omega . \\ \end{aligned} $$

(62)

And this method was widely used in many fields like carbon dioxide emissions forecast (Liu et al. 2022), electricity price forecast (Fu et al. 2020) and electricity demand forecast (Zhang et al. 2018).