Triangular dense fuzzy lock sets

Abstract

This article deals with a triangular dense fuzzy set having special property on Cauchy sequence. In this set, the normality will never be attained unless we unlock by a special key on triangular dense fuzzy set at its final defuzzified state. We give several definitions on triangular dense fuzzy lock sets first and then discuss its locking unlocking property for single-key, double-key, and multiple keys environments with special reference to the convergence of Cauchy sequence. The non-membership function of the proposed lock set has also been studied. The graphical representations of the (non-)membership functions are developed, and the defuzzifications are done by existing methods of dense fuzzy sets as well as cloudy fuzzy sets implicitly. However, we have extended this fuzzy lock set into fuzzy lock matrix to generalize the concept. Finally, we discuss the fields of its practical application and draw a conclusion for better motivation.

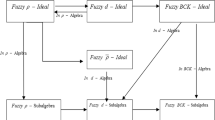
Graphical Abstract of the Triangular Dense fuzzy lock sets

Appendix

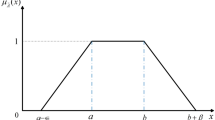
To check the justification of considering the triangular fuzzy lock set as $\widetilde{A} =<a\left( {1-\rho } \right) f_n ,\,a\,,\,a\left( {1+\sigma } \right) f_n >, for\,0<{\rho },\,\sigma \in {\mathcal {R}}$ such that as $n\rightarrow {\infty }, f_n \rightarrow \frac{1}{k},\,k\ne 0$. Then k ( depends upon $\rho ,\,\sigma$) is called the key of the lock set $\widetilde{A}$. In particular we assume, $\widetilde{A} =<a\left\{ {1-\rho \left( {\frac{1}{k}-\frac{1}{n+1}} \right) } \right\} ,\,a,a\left\{ {1+\sigma \left( {\frac{1}{k}-\frac{1}{n+1}} \right) } \right\}>$ whose membership function is given by

$$\begin{aligned} \mu \left( {x,\,n} \right) =\left\{ {{\begin{array}{l} {0\qquad for \, x\, \le a\left( {1-\rho f_n } \right) \,\,or\,a\left( {1+\sigma f_n } \right) \le x} \\ {\frac{x-a\left( {1-\rho f_n } \right) }{a\rho f_n }for\,a\left( {1-\rho f_n} \right) \le x \le a} \\ {\frac{a\left( {1+\sigma f_n } \right) -x}{a\sigma f_n }\,for\,a\le x\le a\left( {1+\sigma f_n } \right) } \end{array} }} \right. \end{aligned}$$

Now to check whether the membership function $\mu \left( {x,n} \right)$ gets values within [0,1] or not.

We assume, for strong fuzzy set, $\rho f_n<1\Rightarrow \rho <1/f_n$ and $\sigma f_n<1\Rightarrow \sigma <1/f_n$ and that for weak fuzzy set, $\rho f_n \ge 1\Rightarrow \rho \ge 1/f_n$ and $\sigma f_n \ge 1\Rightarrow \sigma \ge 1/f_n$.

In particular, $f_n =\left( {\frac{1}{k}-\frac{1}{n+1}} \right) \Rightarrow \hbox {as }n\rightarrow \infty ,\, f_n \rightarrow \frac{1}{k},k\ne 0$. Thus, for strong fuzzy set, we have $\rho<k\,and\,\sigma <k$ and that for weak fuzzy set $\rho \ge k\,and\,\sigma \ge k$.

Moreover, the ratio $\frac{x-a\left( {1-\rho f_n } \right) }{a\rho f_n }$ always lies between [0,1] as because, we always have $a\left( {1-\rho f_n } \right) \le x\le a \Rightarrow 0<x-a\left( {1-\rho f_n } \right) <a\rho f_n \Rightarrow 0\le \frac{x-a\left( {1-\rho f_n } \right) }{a\rho f_n }\le 1$. In particular, let $x=\left[ {a+a\left( {1-\rho f_n } \right) } \right] /2$ then $\frac{x-a\left( {1-\rho f_n } \right) }{a\rho f_n }=\frac{a-a\rho f_n /2-a\left( {1-\rho f_n } \right) }{a\rho f_n }=\frac{a\rho f_n /2}{a\rho f_n }=\frac{1}{2}\in \left[ {0,1} \right]$ and so on.