1 Introduction

The spread of infectious diseases such as COVID-19 may overload healthcare systems and have devastating health, social and economic impacts at different levels (Kaye et al. 2021; Pak et al. 2020; Hossain et al. 2020). Disease modeling is essential to understand spreading dynamics and may provide valuable insights into disease prevention and control.

In this regard, one common approach to describe epidemic dynamics consists of splitting the population into compartments and modeling the rates that describe how individuals move from one compartment to another. Kermack and McKendrick (1927) initially proposed a model of this kind, assigned individuals to three compartments, namely Susceptible (S), Infected (I), and Recovered (R), and modeled the transition events \({\texttt {S}} \rightarrow {\texttt {I}}\) and \({\texttt {I}} \rightarrow {\texttt {R}}\). This model aimed to describe how the number of individuals in each compartment evolves in time by solving a system of differential equations. Several extensions with additional compartments and transition events have been proposed. For instance, we may allow infected individuals to become susceptible again, or we can even include a new compartment—named Exposed (E)—between the susceptible and infected blocks in such a way that it addresses the latent period an individual may go through after being exposed to a disease but before being effectively infected. The last extension is known as SEIR, and both (and others) are described in Keeling and Rohani (2011).

Other extensions can arise from the usual model assumptions. As discussed in Britton et al. (2019), one can assume that individuals are homogeneously and uniformly mixed or primarily in contact with households and close friends. For sexually transmitted diseases, contact may only be defined among one’s sexual partners. Also, we may assume that all individuals have similar responses when exposed to a certain disease; however, people may vary, for example, regarding their immune systems and whether or not they should be included in the susceptible group. Another variable is related to the overall population size; we might assume it is constant over time (or at least approximately constant), but especially for groups observed over longer periods, migration is likely to play a role in the epidemic dynamics.

One could also consider a population divided into strata (e.g., based on gender, age and job type) to account for the different contact frequencies among individuals from these groups. As described by Mossong et al. (2008), elderly individuals have much less contact with other people when compared to younger classes. Age also plays an essential role in the disease severity—for example, there is evidence that the risk of death increases with age for COVID-19 (Wu et al. 2020; Moraga et al. 2020). Moreover, since children were already shown to be more susceptible to influenza than adults (Viboud et al. 2004), age might also impact the infectious rate for some specific diseases. Motivated by that, one can extend the SIR model by including such contact information among age groups to better characterize the interaction in the overall population; that is the approach we take throughout this paper.

Spatial and spatio-temporal statistical models have also been developed to understand disease geographic and temporal patterns, especially over the recent years, due to the increased availability of georeferenced health information (Moraga 2019). However, many of these works that focus on spatio-temporal modeling for infectious disease-related problems analyze areal data from aggregated point-level information or geostatistical data from surveys. For instance, Giuliani et al. (2020) and Lawson and Kim (2021) modeled COVID-19 areal data in space and time in Italy and South Carolina (USA), respectively. On the other hand, methods for dealing with point pattern data for the locations of infected individuals seem to be less explored—partly due to the challenge of obtaining the exact locations of infected individuals. An important example of point pattern data being used in this context comes from Diggle et al. (2005). In such a work, they introduced a log-Gaussian Cox point process model for spatio-temporal disease modeling and applied it to online spatio-temporal surveillance of non-specific gastrointestinal diseases in the United Kingdom. Similarly, there have also been some recent advances in including spatial components in the aforementioned compartment models; e.g., Geng et al. (2021) extended the SIR model to accommodate for the spatial spreading of the studied disease across the considered region by using a spatial kernel, and Lau et al. (2017) proposed a framework based on the SEIR model for describing a disease transmission pattern in space and time.

In this paper, we propose a spatio-temporal modeling framework that describes infectious disease dynamics and allows us to make accurate predictions for the number of infected cases in the future across space. To do so, we integrate the SIR compartment and log-Gaussian Cox process models and use the age-stratified contact information and point pattern data corresponding to the infected individuals’ locations in space-time to fit the model. Although the modeling scheme proposed by Diggle et al. (2005) already decomposes the intensity process into purely spatial, purely temporal and spatio-temporal dependent terms, our approach extends it by using the SIR compartment model output as the temporal component, which has a significant impact on the obtained results, especially when making predictions. More specifically, we propose to model the epidemic spatio-temporal dynamics in two steps: (1) fitting a temporal compartment SIR model taking into account contact patterns of different age groups, and (2) fitting a log-Gaussian Cox process for the point pattern data that represents the locations of infected individuals in the studied region and time interval, such that the mean of such a process depends on the information obtained from the previous step. Also, our fitting procedure for step (2) relies upon a faster computational technique, namely integrated nested Laplace approximation (INLA) (Rue et al. 2009)—as opposed to a Markov chain Monte Carlo (MCMC) algorithm—making it more appealing for practitioners.

The remainder of this paper is as follows. Section 2 presents the prerequisites for SIR modeling and introduces the key concepts in point pattern data analysis. In Sect. 3, we give the details of our proposed framework by describing the integration of the modeling steps in time and space-time. In Sect. 4, we conduct a simulation study to assess the performance of our approach and compare it with a null model that does not incorporate information from the SIR model. In this section, we simulate an epidemic scenario in São Paulo, Brazil, discuss the fitting procedures, and explore the obtained results. Section 5 shows a case study of the number of COVID-19-infected individuals in Cali, Colombia. In the last section, we briefly discuss our methodology and results; we also detail its limitations and possible extensions.

2 SIR and spatial point process models

Here, we briefly review the basics of infectious disease modeling through compartment models; in particular, we consider a SIR compartment model in time that accounts for age classes. We also present the relevant concepts of spatial point processes and describe one possible approach, named “log-Gaussian Cox process,” to model this data.

2.1 SIR model

Suppose we are interested in studying how an infectious disease may spread among individuals living in a given region. To model the evolution of such a disease in time, we can start by dividing the population into three groups, namely Susceptible (S), Infected (I), and Recovered (R), such that individuals are transferred from one compartment to another in the following way: \({\texttt {S}} \rightarrow {\texttt {I}} \rightarrow {\texttt {R}}\). Then, under the assumptions of (1) a homogeneous population with uniform mixing (meaning that individuals meet each other uniformly at random, (2) constant infectious rate and recovery (or death) rate over time, and (3) preserved population mass (that is, the total number of individuals in the population is constant over the total time), we can state the so-called deterministic base-SIR model.

For \(t \in {\mathcal {T}} \subseteq {\mathbb {R}}_{+} = \{x \in {\mathbb {R}}; x \ge 0\}\), let \({\texttt {S}}(t)\), \({\texttt {I}}(t)\), and \({\texttt {R}}(t)\) denote the number of susceptible, infected, and recovered individuals at time t. Also, let \({\texttt {N}}(t) = {\texttt {S}}(t) + {\texttt {I}}(t) + {\texttt {R}}(t)\) denote the total number of individuals in the population, such that \({\texttt {N}}(t) = {\texttt {N}}\), \(\forall t\). Moreover, let \(\beta > 0\) and \(\gamma > 0\) be the infectious and recovery (or death) rates, respectively. In this case, the deterministic base-SIR model describes the evolution of the epidemic through the solution of the following system of Ordinary Differential Equations (ODEs)

$$\begin{aligned} \frac{d{\texttt {S}}(t)}{dt}&= -\beta {\texttt {S}}(t) \frac{{\texttt {I}}(t)}{{\texttt {N}}} \\ \frac{d{\texttt {I}}(t)}{dt}&= +\beta {\texttt {S}}(t) \frac{{\texttt {I}}(t)}{{\texttt {N}}} - \gamma {\texttt {I}}(t) \\ \frac{d{\texttt {R}}(t)}{dt}&= +\gamma {\texttt {I}}(t). \end{aligned}$$

Under initial conditions \(({\texttt {S}}(0), {\texttt {I}}(0), {\texttt {R}}(0))\), such that \({\texttt {R}}(0)\) is usually assumed to be equal to 0, this system can be numerically solved—for instance, one can use the Euler’s Method (Atkinson 2008). Also, \(\beta\) and \(\gamma\) are disease-specific parameters and can be estimated as described in Sect. 3.1.1.

For this so-called base-SIR model, another quantity of interest, \({\mathcal {R}}_0\) (Base Reproductive Number), is essential when studying an infectious disease outbreak. Roughly speaking, \({\mathcal {R}}_0\) represents the expected number of secondary cases arising from a primary case in a completely susceptible population (Blackwood and Childs 2018). In that way, for the above simplistic model, it can be computed as \({\mathcal {R}}_0 = \beta /\gamma\). Here, notice that \({\mathcal {R}}_0\) depends on a “single” infectious case and ignores the individual variability. As we will see next, the base reproductive number is computed differently when considering structured populations.

Often, we cannot assume a homogeneous population with uniform mixing since the number of contacts a person from a particular age group has highly depends on the other individuals’ ages (Mossong et al. 2008). Consequently, we might want to incorporate this contact information for a structured population in our base-SIR model. To do so, we rely on a contact matrix \(C_{ij}\) that represents the average number of contacts made by an individual of age group i with an individual of age group j and on the proportion of individuals in each age group, namely \(f_i\). In this regard, notice that (1) \(C_{ij}\) is not symmetric, and (2) the total number of contacts of group i with group j should be equal to the total number of contacts of group j with group i, i.e., \(C_{ij} \cdot f_i = C_{ji} \cdot f_j\), for all pairs (i, j). Although, as discussed in Fitzgerald et al. (2020), (2) might not hold for all real data sets—especially when one tries to aggregate data from different sources, as we will do.

Based on \(C_{ij}\) and \(f_i\), the age-groups-SIR model will describe the evolution of the epidemic for the different population classes as the solution of the following system of differential equations

$$\begin{aligned} \frac{d{\texttt {S}}_i(t)}{dt}&= -\beta {\texttt {S}}_i(t) \sum _{j}C_{ij}\cdot \frac{{\texttt {I}}_j(t)}{{\texttt {N}}_j} \\ \frac{d{\texttt {I}}_i(t)}{dt}&= +\beta {\texttt {S}}_i(t) \sum _{j}C_{ij}\cdot \frac{{\texttt {I}}_j(t)}{{\texttt {N}}_j} - \gamma {\texttt {I}}_i(t) \nonumber \\ \frac{d{\texttt {R}}_i(t)}{dt}&= +\gamma {\texttt {I}}_i(t), \nonumber \end{aligned}$$
(1)

such that \({\texttt {S}}_i(t)\), \({\texttt {I}}_i(t)\), and \({\texttt {R}}_i(t)\) correspond to the number of susceptible, infected and recovered individuals in group i and at time t, and \({\texttt {N}}_i(t) = {\texttt {N}}_i\), \(\forall t\), is the total number of individuals in group i. The other quantities are defined as before.

From Model (1), notice that the infectious and recovery (or death) rates are still common for all age groups i. Letting \(\beta\) and \(\gamma\) vary with the population class is one possible extension (among many others) of such a model. Also, although there are different methods to determine \({\mathcal {R}}_0\) in this structured-population scenario (Li et al. 2011), the base reproductive number can be numerically computed as the largest eigenvalue of \((\beta /\gamma \cdot M_{ij})\), such that \(M_{ij}\) is a matrix with elements \(C_{ij} \cdot f_{i}/f_j\) for all pairs (i, j) (Blackwood and Childs 2018; Towers and Feng 2012). This method is best known as the “next-generation matrix” (Diekmann et al. 1990, 2010) and has been used in different works (Li et al. 2020; Davies et al. 2020).

Finally, as mentioned before, an analytical solution for systems of differential equations like in Model (1) might not be possible to determine. Instead, we will approach such a problem numerically. To do so, we define a partition of \({\mathcal {T}} = [0, {\text{T}}]\), given by \(\{t_k; k = 0, 1, \ldots , n\}\), such that \(0 = t_0< t_1< \cdots < t_n = {\text{T}}\). For such a discretization, and under initial conditions \(({\texttt {S}}_i(0), {\texttt {I}}_i(0), {\texttt {R}}_i(0))\), \(\forall i\), we can use a solver for initial value problems for ODEs to determine an approximate solution at all \(\{t_k\}_k\). In particular, we will use a solver named lsoda (Hindmarsh 1983; Petzold 1983) when implementing the methodology described in Sect. 3.

2.2 Spatial point process models

This section describes how disease spread can be modeled in space and space-time. In particular, we see how to model the observed space-time locations of infectious individuals in the studied population. To do so, we will briefly discuss the key ideas about point processes and introduce the notation used in the paper.

For each discretized time point \(t_k\) from the previous subsection, we assume that the locations of infectious individuals arise as a realization of a point process in space. For \({\textbf{u}} \in {\mathcal {U}} \subseteq {\mathbb {R}}^2\) and \(t_k\) defined as before, a spatial point process \(\xi (t_k)\) will be defined as a locally finite random subset of \({\mathcal {U}}\); that is, \(\#(\xi (t_k) \cap {\text{A}})\) is finite for all bounded subsets \({\text{A}} \subseteq {\mathcal {U}}\), such that \(\#(x)\) denotes the cardinality of x. From this definition, we will let \(\xi _i(t_k)\) denote a point process in \({\mathcal {U}}\) and at \(t = t_k\) for the locations of infected individuals from a class i in our studied area at a given instant in time. One can refer to Moller and Waagepetersen (2003) for a rigorous introduction to (spatial) point processes.

For spatial point processes, we may define an intensity function \(\lambda : {\mathcal {U}} \rightarrow [0, +\infty )\), such that \(\int _{{\text{A}}} \lambda ({\textbf{u}}; t_k)d{\textbf{u}} < +\infty\), for all bounded \({\text{A}} \subseteq {\mathcal {U}}\), in the following way

$$\begin{aligned} {\mathbb {E}}[{\mathcal {N}}({\text{A}}; t_k)] = \int _{{\text{A}}} \lambda ({\textbf{u}}; t_k)d{\textbf{u}},\; {\text{A}} \subseteq {\mathcal {U}}, \end{aligned}$$

where \({\mathcal {N}}({\text{A}}; t_k)\) counts the number of points in \({\text{A}}\) at \(t = t_k\). Thus, \(\lambda _i({\textbf{u}}; t_k)\) will correspond to the intensity function of the point process \(\xi _i(t_k)\) for all classes i.

Spatial point processes can be modeled using a Poisson point process. A point process \(\xi (t_k)\) on \({\mathcal {U}}\) is a Poisson point process with intensity function \(\lambda ({\textbf{u}}; t_k)\) if the following properties are satisfied

  1. 1.

    For any bounded \({\text{A}} \subseteq {\mathcal {U}}\), \({\mathcal {N}}({\text{A}}; t_k) \sim {\text{Poisson}}\left( \int _{{\text{A}}} \lambda ({\textbf{u}}; t_k)d{\textbf{u}}\right)\); and

  2. 2.

    For any bounded \({\text{A}} \subseteq {\mathcal {U}}\) and \(n \in {\mathbb {N}}\), conditional on \({\mathcal {N}}({\text{A}}; t_k) = n\), points in \(\xi (t_k) \cap {\text{A}}\) are independent and identically distributed with density proportional to \(\lambda ({\textbf{u}}; t_k)\).

Therefore, getting back to the disease spread modeling problem, \(\xi _{i}(t_k)\) would be the process that describes the locations, at \(t_k\), of the infected individuals in age group i. Also, if \(\xi _{i}(t_k)\) is a Poisson point process, its average will depend on the corresponding intensity function \(\lambda _i({\textbf{u}}; t_k)\).

2.2.1 Log-Gaussian Cox process

Due to its simplicity, the Poisson point process may not be valid for describing more complex scenarios. However, such a process can be extended to a more general class of models named Cox process (Cox 1955). A Cox process can be seen as a doubly stochastic process since its intensity function is a random process itself. More specifically, \(\xi (t_k)\) is a Cox process driven by \(\Lambda ({\textbf{u}}; t_k)\) if

  1. 1.

    \(\{\Lambda ({\textbf{u}}; t_k); {\textbf{u}} \in {\mathcal {U}}\}\) is a non-negative valued stochastic process, and

  2. 2.

    Conditional on \(\{\Lambda ({\textbf{u}}; t_k) = \lambda ({\textbf{u}}; t_k); {\textbf{u}} \in {\mathcal {U}}\}\), \(\xi (t_k)\) is a Poisson process with intensity function \(\lambda ({\textbf{u}}; t_k)\).

A particular case of a Cox process named log-Gaussian Cox process can be constructed by setting \(\log \{\Lambda ({\textbf{u}}; t_k)\} = \mu ^{\star }({\textbf{u}}; t_k) + \zeta ({\textbf{u}}; t_k)\), such that \(\mu ({\textbf{u}}; t_k) = \exp \{\mu ^{\star }({\textbf{u}}; t_k)\}\) is possibly interpreted as the mean structure of \(\Lambda ({\textbf{u}}; t_k)\), and \(\zeta ({\textbf{u}}; t_k)\) is a stationary Gaussian process, such that \({\mathbb {E}}(\zeta ({\textbf{u}}; t_k)) = -\sigma ^2/2\), \(\forall k\) and \({\textbf{u}}\), and \({\text{Cov}}(\zeta ({\textbf{u}}_1; t_k), \zeta ({\textbf{u}}_2; t_k)) = \phi (h; t_k) = \sigma ^2 \rho (h; t_k)\), where \(h = ||{\textbf{u}}_1 - {\textbf{u}}_2||\) and \(\sigma ^2\) is the variance of \(\zeta ({\textbf{u}}; t_k)\). In this case, \({\mathbb {E}}(\Lambda ({\textbf{u}}; t_k)) = \mu ({\textbf{u}}; t_k)\), and \({\text{Cov}}(\Lambda ({\textbf{u}}_1; t_k), \Lambda ({\textbf{u}}_2; t_k)) = \psi ({\textbf{u}}_1, {\textbf{u}}_2; t_k) = \tau ^2 \theta (\mathbf {u_1}, \mathbf {u_2}; t_k) = \mu ({\textbf{u}}_1; t_k) \mu ({\textbf{u}}_2; t_k) [\exp \{\phi (||{\textbf{u}}_1 - {\textbf{u}}_2||; t_k)\} - 1]\), where \(\tau ^2 = 2\mu ({\textbf{u}}; t_k)[\exp \{\sigma ^2\} - 1]\) is the variance of \(\Lambda ({\textbf{u}}; t_k)\).

We set \(\xi _i(t_k)\), \(\forall i\), as log-Gaussian Cox processes for the events of observing infected individuals in each age class and at \(t_k\). In particular, the corresponding Gaussian processes \(\zeta _i({\textbf{u}}; t_k)\) will describe the spatio-temporal dependence structure for the underlying processes \(\Lambda _i({\textbf{u}}; t_k)\). In Sect. 3.2, we see different ways to model \(\zeta _i({\textbf{u}}; t_k)\).

3 Methodology

We propose a model to describe how infectious diseases evolve in space and time and how to make predictions for the future number of cases across the study region. We do this by integrating the SIR compartment modeling in time and a point process modeling approach in space-time. By combining these methods, we incorporate knowledge about the mechanistic approach that drives the temporal dynamics into the model that accounts for spatial dependence.

Our approach is divided into two steps. First, we aggregate the data in the whole region for each discretised time window and estimate the epidemic dynamics in time using a SIR model. This gives us the corresponding curves for the number of infected individuals for all age groups i and at all time points \(t_k\). Then, for each population class, we estimate the intensity of the spatial-temporal point process that originated each observed point pattern of infected individuals. We do this by incorporating the estimates of the total number of infectious derived from the SIR model into the mean component of the point process and adding a spatio-temporal random structure to take variation into account. This approach allows us to describe past spatio-temporal patterns and predict the spatio-temporal evolution of the disease in future times. Figure 1 shows a diagram that illustrates such a procedure.

Fig. 1
figure 1

Diagram for the spatio-temporal modeling approach of infected individuals in all age groups i. From left to right, we have the infected individuals’ locations (“\(\circ\)” denotes Group 1 and “\(\times\)” denotes Group 2), the observed and estimated \({\texttt {I}}_{i}(t_k)\) curves (here, notice that we collected data up to \(t_{50}\) and made predictions up to \(t_{99}\)), the base functions that represent the population at risk (see Sect. 3.2), and the estimated intensity functions for all time windows

Full size image

Throughout this paper, we will use the following notation. The observed data are the locations and times of infected individuals for each age group i—we will denote them by \(\{\xi _i(t_k)\}_k\) for all \(t_k\). That is, for \(t \in {\mathcal {T}} = [0, \text {T}]\), such that \({\mathcal {T}}\) is partitioned into \(\{t_k; k = 0, 1, \ldots , n\}\) and \({\textbf{u}} = (u_1, u_2) \in {\mathcal {U}} \subseteq {\mathbb {R}}^2\), we have that \(\{\xi _i(t_k)\}_k\), for all i, are sequences of spatial point patterns in \({\mathcal {U}}\) observed at time \(t = t_k\), such that the corresponding point process describes the locations of the infected individuals in each class and time window.

3.1 Temporal modeling

Our first step concerns modeling and estimating the temporal structures of the disease spread process in the population of interest. In this regard, the counting processes for the number of susceptible, infected and recovered individuals in all age classes, namely \({\texttt {S}}_i(t)\), \({\texttt {I}}_i(t)\), and \({\texttt {R}}_i(t)\), respectively, will be modeled according to Model (1).

Based on data given by a set of locations for each observed infected individual, denoted by \(\{\xi _i(t_k)\}_k\), such that \(k \in \{0, 1, \ldots , n\}\), we can start by aggregating all location observations over space in such a way that \({\texttt {i}}_i(t_k) = \#(\xi _i(t_k))\), \(\forall i, k\). Therefore, \({\texttt {i}}_i(t)\) will correspond to the observed counting process for the number of infected individuals in each group at \(t = t_0, t_1, \ldots , t_n\). We can estimate the parameters based on Model (1) from such data and solve for \({\texttt {S}}_i(t_k)\), \({\texttt {I}}_i(t_k)\), and \({\texttt {R}}_i(t_k)\), \(\forall i, k\), for inference and prediction.

3.1.1 Inference and prediction in time

A solution for Model (1) can be approximately computed using a numerical solver, as described in Sect. 2.1. In this way, for a set of initial values \(({\texttt {S}}_i(0), {\texttt {I}}_i(0), {\texttt {R}}_i(0))\), \(\forall i\), and initial guesses for \(\beta\) and \(\gamma\), we can solve the system of ODEs for \({\texttt {S}}_i(t_k)\), \({\texttt {I}}_i(t_k)\), and \({\texttt {R}}_i(t_k)\) by employing such a method. For later reference, we will name these solutions \({\mathtt{S}}_i^{{\mathtt{ODE}}}(t_k)\), \({\mathtt{I}}_i^{{\mathtt{ODE}}}(t_k)\), and \({\mathtt{R}}_i^{{\mathtt{ODE}}}(t_k)\), respectively.

Suppose we have obtained \({\mathtt{i}}_i(t_k)\), \(\forall i, k\), i.e., the number of infected individuals in all groups and at all time points. One way to model such data is by assuming they come from a specific probability distribution with the mean given by the ODE solution \({\mathtt{I}}_i^{{\mathtt{ODE}}}(t_k)\), \(\forall i, k\). In particular, as we are dealing with counting data and aiming to account for the possible overdispersion when fitting a Poisson model, we will assume a Negative Binomial distribution for the observed number of infected individuals, that is,

$$\begin{aligned} {\mathtt{I}}_i(t_k) \sim {\text{Negative Binomial}}({\mathtt{I}}_{i}^{{\mathtt{ODE}}}(t_k), \varphi ), \end{aligned}$$
(2)

such that \(\varphi\) is the overdispersion parameter; this implies that \({\mathbb {E}}({\mathtt{I}}_i(t_k)) = {\mathtt{I}}_{i}^{{\mathtt{ODE}}}(t_k)\) and \({\text {Var}}({\mathtt{I}}_i(t_k)) = {\mathtt{I}}_{i}^{{\mathtt{ODE}}}(t_k)(1 + (1 / \varphi ) \cdot {\mathtt{I}}_{i}^{{\mathtt{ODE}}}(t_k)).\)

For such an approach, notice that this is an iterative procedure. (I) First, we set initial guesses for \(\beta\), \(\gamma\), and \(\varphi\). (II) Then, given the parameter values, we solve Model (1) for \({\mathtt{S}}_i(t_k)\), \({\mathtt{I}}_i(t_k)\), and \({\mathtt{R}}_i(t_k)\). (III) After that, we plug the \({\mathtt{I}}_i^{{\mathtt{ODE}}}(t_k)\) curve into the mean component of Model (2) and evaluate the corresponding likelihood function. (IV) Next, regardless of the estimation framework, and after updating the values of \(\beta\), \(\gamma\), and \(\varphi\), we get back to step (II) and repeat this sequential procedure until convergence.

The model from Eqs. (1) and (2) can be fitted in different ways. Here, we adopt a Bayesian framework and use RStan (Stan Development Team 2021) to estimate the posterior distribution of \(\varvec{\theta } = (\beta , \gamma , \varphi )^{\top }\), always assuming reasonable prior distributions for \(\beta\), \(\gamma\), and \(\varphi\) and the Negative Binomial likelihood for the observed counting. Also, when making predictions, assuming we can generate quantities from the fitted model, we need to solve Eq. (1) for \({\mathtt{S}}_i(t_k)\), \({\mathtt{I}}_i(t_k)\), and \({\mathtt{R}}_i(t_k)\) for any i and any k beyond the observation range.

3.2 Spatio-temporal modeling

Once we have estimated the model parameters and, therefore, the \({\mathtt{I}}_i(t_k)\) curves, we can start modeling the intensity functions for the spatial processes for all age groups i at all times \(t_k\). In particular, we assume that the observed point patterns are originated from log-Gaussian Cox processes evaluated at the same partition of \({\mathcal {T}} = [0, {\text{T}}]\) defined before, namely \(\{t_k; k = 0, 1, \ldots n\}\). Thus, the counting number of infected individuals in each age group i and at \(t_k\), namely \({\mathcal {N}}_i(t_k)\), will be modeled as follows

$$\begin{aligned} {\mathcal {N}}_i(t_k)|\Lambda _i({\textbf{u}}; t_k) = \lambda _i({\textbf{u}}; t_k) \sim \text {Poisson}\left( \int _{{\mathcal {U}}}\lambda _i({\textbf{u}}; t_k)d{\textbf{u}}\right) , \end{aligned}$$

and the corresponding intensity functions will be described by

$$\begin{aligned} \Lambda _i({\textbf{u}}; t_k)&= \mu _i({{\textbf {u}}}; t_k) \cdot \exp \{\zeta _i({\textbf{u}}; t_k)\} \end{aligned}$$
(3)

such that all quantities are defined as in Sect. 2.2.1. Here, \(\mu _i({\textbf{u}}; t_k)\) represents the large-scale component of the model, and \(\exp \{\zeta _i({\textbf{u}}; t_k)\}\) represents the random variation around it. This model formulation for \(\Lambda _i({\textbf{u}}; t_k)\) is similar to the one proposed by Diggle et al. (2005). Notice that although \(\zeta _i({\textbf{u}}; t_k)\) is a stationary process, if \(\mu _i({\textbf{u}}; t_k)\) is a non-constant function for a fixed \(t_k\), then \(\Lambda _i({\textbf{u}}; t_k)\) has spatially varying mean and covariance functions depending on the points’ locations. In this case, the resulting Cox process with such intensity is called an intensity-reweighed stationary point process (Baddeley et al. 2000), similar to a real-valued process with varying mean and stationary residuals (Diggle et al. 2013).

Concerning Eq. (3), we have to define the mean structure \(\mu _i({\textbf{u}}; t_k)\) and the correlation function \(\rho _i(h; t_k)\). Starting with \(\mu _i({\textbf{u}}; t_k)\), we will set it as a function of the previously estimated \({\mathtt{I}}_i(t_k)\) curve, \(\forall i, k\). We aim to have the expected number of infected individuals in the studied region somehow similar to what we estimated using the compartment model. This strategy will be beneficial when making predictions, as discussed in Sect. 4. In particular, we set the mean structure to

$$\begin{aligned} \mu _i({\textbf{u}}; t_k)&= \lambda _{0, i}({\textbf{u}}; t_k) \cdot {\mathtt{I}}_i(t_k) \cdot \exp \{\omega _{1, i} \, x_{1, i}({\textbf{u}}; t_k) \nonumber \\&\quad + \cdots + \omega _{p, i} \, x_{p, i}({\textbf{u}}; t_k)\}, \end{aligned}$$
(4)

where \(\lambda _{0, i}({\textbf{u}}; t_k)\) is a non-negative real-valued function, such that \(\int _{{\mathcal {U}}}\lambda _{0, i}({\textbf{u}}; t_k) = 1\). In practice, \(\lambda _{0, i}({\textbf{u}}; t_k)\) will be set as proportional to the population density function for class i. Here, notice that \(\lambda _{0, i}({\textbf{u}}; t_k)\) depends on \(t_k\) and might evolve over time if the population structure also changes. By setting it that way, we are using the total population distribution as a proxy for the locations of the individuals at risk of infection. Also, for each group, we can include a vector of p spatio-temporal covariates representing risk factors \((x_{1, i}({\textbf{u}}; t_k), \ldots x_{p, i}({\textbf{u}}; t_k))\) with associated coefficients \((\omega _{1, i}, \ldots , \omega _{p, i})^{\top }\).

Now, to define the covariance structure of \(\zeta _i({\textbf{u}}; t_k)\), first, notice that it can be written as

$$\begin{aligned} \zeta _i({\textbf{u}}; t_k) = \beta _{0, i} + \vartheta _i({\textbf{u}}; t_k), \end{aligned}$$

where \(\beta _{0, i}\) is the mean component of \(\zeta _i({\textbf{u}}; t_k)\), and \(\vartheta _i({\textbf{u}}; t_k)\) is a zero-mean spatially dependent Gaussian process with covariance function \(\phi _i(h; t_k) = \sigma _i^2 \rho _i(h; t_k)\). In particular, we assume a Matérn model (Matérn 1960) for the correlation function, a flexible correlation model appearing in many fields. Thus,

$$\begin{aligned} \rho _i(h; t_k) = \frac{1}{2^{\nu _i - 1}\Gamma (\nu _i)}(\kappa _i \cdot h)^{\nu _i} \,\text {K}_{\nu _i}(\kappa _i \cdot h), \end{aligned}$$
(5)

such that \(\nu _{i, k} = \nu _i\) and \(\kappa _{i, k} = \kappa _i\), \(\forall k\) are unknown parameters, and \(\text {K}_{\nu _i}(\cdot )\) is a modified Bessel function of \(2^{\text {nd}}\) order for age class i. For later reference, we will name this approach \({\mathtt{REF}}\).

Aiming for more flexible models, we can still add other structures to the REF model, for instance, independent and identically distributed (i.i.d.) and autoregressive components. More specifically, we will also define the IID and AR1 model extensions. The IID model is defined as

$$\begin{aligned} \zeta _i({\textbf{u}}; t_k) = \beta _{0, i} + \vartheta _i({\textbf{u}}; t_k) + \varepsilon _i({\textbf{u}}; t_k), ~\forall i, \end{aligned}$$

where \(\varepsilon _i({\textbf{u}}; t_k)\) is a zero-mean independent Gaussian process with variance \(\sigma ^{2}_{i, \varepsilon }\). Here, \(\varepsilon _i({\textbf{u}}; t_k)\) acts like an unstructured exchangeable component modeling the uncorrelated noise in space and time. Also, the AR1 model is defined as

$$\begin{aligned} \zeta _i({\textbf{u}}; t_k) = \beta _{0, i} + \vartheta _i({\textbf{u}}; t_k) + \varepsilon _i({\textbf{u}}; t_k) + \upsilon _i(t_k), ~\forall i, \end{aligned}$$

such that

$$\begin{aligned} {\upsilon _i(t_k) = \alpha _i \upsilon _i(t_{k-1}) + \varrho _i(t_k), \text { for } k = 1, \ldots , n, } \end{aligned}$$

where \(|\alpha _i| < 1\), \(\forall i\), and \(\varrho _i(t_k)\) is a zero-mean temporally independent Gaussian process with variance \(\sigma _{i, \varrho }^2\). In that case, \(\upsilon _i(t_k) \sim \text {Normal}(0, \sigma ^2_{i, \varrho }/(1 - \alpha _i^2))\), \(\forall k\), such that \({\text{Cov}}(\nu _i(t_k), \nu _i(t_{k + m})) = \alpha _i^{|m|} \cdot \sigma _{i, \varrho }^2 / (1 - \alpha _i^2)\). Also, notice that \(\upsilon _i(t_k)\) does not depend on the location, and therefore, the corresponding Cox process can account for spatial clustering but not temporal clustering. In that way, we are not modeling the local dependence of \(\zeta _i({\textbf{u}}; t_k)\) over time; instead, the temporal dependence is commonly included for all \({\textbf{u}} \in {\mathcal {U}}\). To overcome this issue, one could define \(\varrho _i\), \(\forall i\), as a zero-mean temporally independent but spatially dependent Gaussian process for each \(t_k\) with, for example, a Matérn covariance model. However, this would result in a more computationally expensive inference procedure that typically requires larger data sets.

As a final remark, notice that another natural extension would be including a random effect for the interaction between space and time [e.g., as in Knorr-Held (2000)]. However, due to the typical number of data points observed in our infectious-disease-modeling problems, it may become computationally prohibitive fitting such models.

3.2.1 Inference and prediction in space and time

The final model for the counting number of infected individuals in all age groups i at \(t_k\) is specified as follows

$$\begin{aligned} {\mathcal {N}}_i(t_k)|\Lambda _i({\textbf{u}}; t_k)&= \lambda _i({\textbf{u}}; t_k) \sim {\text{Poisson}}\left( \int _{{\mathcal {U}}}\lambda _i({\textbf{u}}; t_k)d{\textbf{u}}\right) , ~\forall i, k \\ \Lambda _i({\textbf{u}}; t_k)&= \mu _i({\textbf{u}}; t_k) \cdot \exp \{\zeta _i({{\textbf{u}}; t_k})\} \nonumber \\ \mu _i({\textbf{u}}; t_k)&= \lambda _{0, i}({\textbf{u}}; t_k) \cdot {\mathtt{I}}_i(t_k) \nonumber \\ \zeta _i({\textbf{u}}; t_k | \varvec{\eta }_i)&\sim {\text {Gaussian Process}} (\beta _{0, i}, \phi _i(h; t_k | \varvec{\eta }_i)) \nonumber \\ \varvec{\eta }_i&\sim {\text {priors}}, \nonumber \end{aligned}$$
(6)

where \(\phi _i(h; t_k | \varvec{\eta }_i)\) is a covariance function that depends on the selected model from Sect. 3.2, and \(\varvec{\eta }_i\) is a vector of parameters and hyperparameters.

We fit this model, using R-INLA (Rue et al. 2009), by employing the gridding approach described by Moraga (2020). Specifically, we create a regular grid over the studied region and model the number of occurring events in each grid cell \(c_j\) as \({\mathcal {N}}_{i, j}(t_k) \sim {\text {Poisson}}(\theta _{i, j, k})\), such that \(\theta _{i, j, k} = \int _{c_j}\lambda _i({\textbf{u}}; t_k)d{\textbf{u}}\). In that way, for sufficiently small cells, we can approximate such an integral by \(|c_j| \cdot \lambda _i({\textbf{u}}; t_k)\), for any \({\textbf{u}} \in c_j\), where \(|\cdot |\) denotes area. Also, in R-INLA, \(\zeta _i({{\textbf{u}}; t_k})\) is defined as a zero-mean process; therefore, to accommodate this change in the mean of the intensity process, we must include an intercept in the linear predictor for the Poisson regression formula when fitting the model.

As a final comment, notice that if we have “well predicted” values for \({\mathtt{I}}_i(t_k)\) for some k in the future, the mean structure of the spatio-temporal modeling, namely \(\mu _i({{\textbf {u}}}; t_k)\), can greatly help us to explain \(\lambda _i({\textbf{u}}; t_k)\) for non-observed time points, as we will see in Sect. 4.

4 Simulation study

In this section, we perform a simulation study to assess the performance of our model and compare it with a null model in which information from the estimated \({\mathtt{I}}_i(t_k)\) curves is not used. Since the exact locations of infected individuals over time are still difficult to obtain (Hernández-Orallo et al. 2020), we use a combination of real and synthetic data. Specifically, we consider many scenarios and simulate point patterns for the locations of infected individuals in all age groups i observed over space and time. Then, we fit a null and our proposed model to assess and compare their prediction performances. The code to reproduce such analyses is available on https://github.com/avramaral/PP_SIR.

4.1 Data simulation

We consider as a study region an area of approximately 3 km\({}^{2}\) in São Paulo, Brazil (Figure SF1, Supplementary Information). In such a region, we use the estimated population size (WorldPop 2020) defined in each of the (approximately) 100 \(\times\) 100 m cells (with 39,040 individuals in total) as a base function that mimics the real intensity that describes how infectious individuals are distributed over space. Then, we simulate daily observations for 100 days.

We divide the population into three age groups, namely 0–19, 20–59, and 60+, so that the proportion of individuals in Brazil that fall into each cathegory is given by 0.33, 0.60, and 0.07, respectively (Nations 2019). The contact matrix \(C_{ij}\) is also defined for the same three age groups and determined by the estimates from Prem et al. (2017) (Table ST1, Supplementary Information). Population age distribution and contact matrix data were retrieved using the COVOID package (Fitzgerald et al. 2020).

Regarding the simulation of the infected curves, we will do this in two ways. First, we will assume the data comes from the model described by Eqs. (1) and (2). Second, to assess how well our approach behaves for an incorrectly specified model for the temporal component, we will also generate data from a different model, i.e., we will violate the SIR assumptions and conduct a sensitivity analysis under these conditions. In particular, we will simulate from the model described in Section SS2 (Supplementary Information), based on Chen et al. (2016) and Held et al. (2005). For reference, name it Autoregressive Conditional Negative Binomial (ACNB) model.

Given \(\beta\), \(\gamma\) and \(\varphi\), for the SIR scenarios, we can simulate the epidemic dynamics from Eqs. (1) and (2) and sample it at \(t_k\), \(\forall k\). In particular, when considering the SIR temporal modeling, notice that our goal is estimating the \({\mathtt{S}}_i(t_k)\), \({\mathtt{I}}_i(t_k)\), and \({\mathtt{R}}_i(t_k)\) curves for all age groups i. To do this, we will consider two scenarios, namely “early peak” (EP) and “flat curve” (FC) for the infected individuals. The corresponding parameters \(\beta\), \(\gamma\), and \(\varphi\), will be set as 0.04, 0.2, and 100 for scenario EP and 0.0175, 0.1, and 100 for scenario FC. The chosen scenarios aim to cover the situations in which (1) we observe a high peak for the infectious in the very beginning and, therefore, it is easy to make predictions for future times under the SIR model assumptions, and (2) the epidemic is still half-way through and, therefore, it is not trivial to predict what will happen next. Finally, the simulated number of infected individuals for the SIR model in each group and under each scenario (EP and FC) can be seen in Figure SF2 (Supplementary Information). Similarly, the data simulated from the ACNB model can be seen in Figure SF3 (Supplementary Information).

Once we have simulated the \({\mathtt{I}}_i(t_k)\) curves, \(\forall i, k\), the true generated intensity functions will be sampled from the following model

$$\begin{aligned} \Lambda _i({\textbf{u}}; t_k)&= \lambda _{0, i}({\textbf{u}}; t_k) \cdot {\mathtt{I}}_i(t_k) \cdot \exp \{\zeta _i({\textbf{u}}; t_k)\},\\&\quad {\text { for each } } i {\text { and }} k = 0, 1, \ldots , 99, \end{aligned}$$

where \(\lambda _{0, i}({\textbf{u}}; t_k)\) is the normalized populational grid, and \(\zeta _i({\textbf{u}}; t_k)\) is defined according to the IID or AR1 models, as in Sect. 3.2, with parameters specified in Table ST3 (Supplementary Information). Then, the number of infected individuals and their respective locations will be generated from a Poisson process with the corresponding intensity function \(\lambda _i({\textbf{u}}; t_k)\).

4.2 Fitted models

Based on the data described in Sect. 4.1, we will fit a null model (\({\mathcal {M}}_0\)) and our proposed alternative model (\({\mathcal {M}}_1\)). The difference is that information from the estimated \({\mathtt{I}}_i(t_k)\) curves will not be used for the null model. In particular, for the counting number of infected individuals in all age groups i and at \(t_k\) modeled as follows

$$\begin{aligned} {\mathcal {N}}_i(t_k)|\Lambda _i({\textbf{u}}; t_k) = \lambda _i({\textbf{u}}; t_k) \sim {\text {Poisson}}\left( \int _{{\mathcal {U}}}\lambda _i({\textbf{u}}; t_k)d{\textbf{u}}\right) , \end{aligned}$$

the null model (\({\mathcal {M}}_0\)) will be given by

$$\begin{aligned} \Lambda _i({\textbf{u}}; t_k)&= \exp \{\omega _{0, i} + \zeta _i({\textbf{u}}; t_k)\}, \end{aligned}$$
(7)

such that \(\omega _{0, i}\) is an unknown intercept, and the alternative (\({\mathcal {M}}_1\)) model will be given by

$$\begin{aligned} \Lambda _i({\textbf{u}}; t_k)&= \mu _{i}({\textbf{u}}; t_k) \cdot \exp \{\zeta _i({\textbf{u}}; t_k)\}, \end{aligned}$$
(8)

such that \(\mu _{i}({\textbf{u}}; t_k)\) is defined as in Eq. (4); that is, the alternative model will depend on both the base function \(\lambda _{0, i}({\textbf{u}}; t_k)\) and the estimated \({\mathtt{I}}_i(t_k)\) curve. Also, \(\zeta _i({\textbf{u}}; t_k)\) will be defined in all scenarios based on one of the structures introduced in Sect. 3.2, namely IID and AR1.

4.3 Implementation and results

For the simulated data sets introduced in Sect. 4.1, we can fit the models (both null and alternative) that we have just described. In particular, the temporal component will be modeled as in Sect. 3.1 with the SIR approach, and the spatial modeling for all age groups i and all \(t_k\) will be performed as detailed in Sect. 3.2; that is, we will consider the point pattern of infected individuals in each of the discretized time windows to estimate and predict the corresponding intensity functions. Here, we specify the remaining terms and analyze the obtained results.

Starting with the temporal modeling, the number of individuals in each compartment, the \({\mathtt{S}}_i(t_k)\), \({\mathtt{I}}_i(t_k)\), and \({\mathtt{R}}_i(t_k)\) curves, \(\forall i, k\), will be described by Eq. (1)—with an approximated solution obtained as mentioned in Sect. 2.1. Also, the stochasticity from the sampling procedure will be given by Eq. (2). In that case, the prior distributions were specified as \({\text {Normal}}(0.5, 1)\) for \(\beta\) and \(\gamma\) and \({\text {Normal}}(1, 100)\) for \(\varphi\), all truncated at 0. This choice for the priors is vaguely enough for our problem, and the chains for the posterior sampled values were well mixed in all cases (Figures SF4 and SF5 for the data generated from the SIR model (scenarios EP and FC, respectively), and Figure SF6 for the data generated from ACNB model—Supplementary Information). In particular, using RStan, we set the number of chains, the number of iterations and the burn-in size as 4, 4, 000, and 2, 000, respectively.

Furthermore, as we also want to make predictions, all models throughout this section will be fitted with data up to \(t_{49}\). The estimated parameters for all scenarios, namely SIR-EP, SIR-FC, and ACNB, can be seen in Table 1. Additionally, the estimated curves for the three scenarios (SIR-EP, SIR-FC, and ACNB) and age group 20–59 can be seen in Fig. 2. The other two sets of fitted curves for the age groups 0–19 and 60+ can be seen in Figure SF7 (Supplementary Information).

Table 1 Estimated parameters (and 95% equal-tail credible interval) for the two SIR scenarios, namely EP and FC, and for the model fitted with data from ACNB. Models were fitted with data up to \(t_k = 49\)
Full size table
Fig. 2
figure 2

Estimated \({\mathtt{I}}_i(t_k)\) curves (black curves) for the age group 20–59 in the two SIR scenarios, namely EP (left panel) and FC (middle panel), and the ACNB scenario (right panel). Models were fitted with data up to \(t_{49}\) (vertical dashed line). The red curves correspond to the observed number of infected individuals over time

Full size image

From Table 1, we can see that the model parameters for the SIR scenarios were well estimated, and their true values were always within the 95% equal-tail estimated credible interval. Also, from Figs. 2 and SF7 (Supplementary Information), the estimated curves (given by the solution of Model (1) averaged over all sampled \(\beta\), \(\gamma\), and \(\varphi\) parameters) approximate the observed count data well. However, for the data that violates the SIR assumptions, i.e., data from the ACNB model, the corresponding fitted model presents higher variability (expected since the fitted SIR model is not that flexible). Moreover, based on Figs. 2 and SF7 (Supplementary Information) for the ACNB scenario, we can observe that the estimated curves under this setting do not approximate well the true ones. Nonetheless, as we will confirm next, even in that case, our alternative model still performs better than the null model when using such a poorly fitted mean component.

Provided that we have fitted the temporal model and estimated the \({\mathtt{I}}_i(t_k)\) curves, \(\forall i, k\), we can now employ our modeling approach in space-time, as in Sect. 3.2. Here, we will use the same regular grid over \({\mathcal {U}}\) as in Figure SF1 (Supplementary Information) for the inference and prediction steps. Also, as discussed in Sect. 3, we will fit the spatio-temporal model under different scenarios (IID and AR1); in particular, we will compare a null model (\({\mathcal {M}}_0\)), as in Eq. (7), with our proposed alternative (\({\mathcal {M}}_1\)) model, as in Eq. (8). So that we can assess whether bringing information (even if it is not good quality) from the SIR compartment modeling approach, as in Eq. (4), helps to describe the intensity function for the observed point processes and make predictions. Table 2 lists all possible combinations for data generation and model fitting.

Table 2 Different space-time scenarios (indexed by the “ST Sce.” columns) under which we will generate data and fit the spatio-temporal models. “T Sce.” refers to the two possible SIR scenarios, namely EP and FC, and the ACNB one—all for temporal data generation. “Data Gen.” refers to the spatio-temporal models, as in Sect. 3.2, when generating \(\zeta _i({\textbf{u}}; t_k)\). Furthermore, “Model Fit.” refers to the possible fitted models (\({\mathcal {M}}_0\) and \({\mathcal {M}}_1\)) with the different proposed spatio-temporal structures (IID and AR1)
Full size table

To fit Model (6), we used R-INLA and set the priors for the parameters and hyperparameters as the default distributions, \(\omega _{0, i} \sim {\text {Normal}}(0, (1/\iota _{0, i}))\), such that \(\iota _{0, i} = 0\), \(\log (\sqrt{8\nu _i}/\kappa _i) \sim {\text {LogGamma}}(1, 5 \times 10^{-5})\), \(\log (1/\sigma ^2_i) \sim {\text {LogGamma}}(1, 0.01)\), \(\log (1/\sigma ^2_{i, \varepsilon }) \sim {\text {LogGamma}}(1, 5 \times 10^{-5})\), \(\log ((1 + \alpha _{i})/(1 - \alpha _i)) \sim {\text {Normal}}(0, (1/0.15))\), and \(\log ((1/\sigma ^2_{i, \varrho }) \cdot (1 - \alpha _{i})) \sim {\text {LogGamma}}(1, 5 \times 10^{-5})\). Besides, the Gaussian processes \(\zeta _i({\textbf{u}}; t_k)\), \(\forall i\) were defined as following a Matérn model for the correlation structure, as in Eq. (5), with smoothing parameter \(\nu _i = \nu\), for all age groups i. Then, all possible combinations for the “data generation procedure” and “model fitting” from Table 2 were fitted for data observed up to \(t_{49}\). In that way, based on the samples drawn from the posterior distributions of the model parameters, we could directly estimate \(\lambda _i({\textbf{u}}; t_k)\) for all i and \(t_k\), such that \(k \le 49\), and predict all remaining k. Figure SF8 (Supplementary Information) shows the estimated number of infected individuals at \(t_{49}\), age group 20–59, and space-time scenario 16, as per Table 2. As a remark, under this setting, the true number of infected individuals in the entire region was 7,435, while the estimated value was, rounding it to zero decimal places, 7,444 (with a 95% equal-tail credible interval given by 6,781—8,160).

Following this procedure, we could fit our model and estimate (and predict) the intensity functions for all age groups—which is the same as estimating (and predicting) the number of infected individuals in each cell. As described in Sect. 3.2.1, assuming we have “reasonably well predicted” values for \({\mathtt{I}}_i(t_k)\), we expect better quality prediction when describing the underlying process that generated the observed point pattern. This happens since \({\mathtt{I}}_i(t_k)\) is plugged-in as the mean of the spatio-temporal process, which improves the overall model performance. The following section assesses the null and alternative models regarding their error for the estimated or predicted intensity functions compared to the true values for all scenarios listed in Table 2.

4.3.1 Model assessment

Aiming to compare the null model (\({\mathcal {M}}_0\)) with our proposed alternative model (\({\mathcal {M}}_1\)), we compute a measure of error for all scenarios from Table 2 for the difference between the estimated (or predicted) values and the true values for a quantity proportional to the intensity function. In particular, we analyze the difference between the estimated and true values for the number of infected individuals per cell—more specifically, we are interested in such errors when making predictions. However, we might want to use a scale-independent error measure to compare the data sets with different scales, such as data from different age groups. The Absolute Percentage Error (APE) has been widely employed in this regard (Bowerman et al. 2005), and it can be defined as follows for each group i and at \(t_k\),

$$\begin{aligned} {\text {APE}}_{i, j, k} = \left| \frac{(f_{i, j, k} - {\hat{f}}_{i, j, k})}{f_{i, j, k}}\right| , \end{aligned}$$

where \(f_{i, j, k}\) and \({\hat{f}}_{i, j, k}\) correspond to the true and predicted number of infectious in group i, cell \(c_j\), and \(t_k\), respectively. However, since it produces infinite values if \(f_{i, j, k} = 0\) for any j, it may not be suitable for our problem. Instead, we will use a modified version of APE, namely Arctangent Absolute Percentage Error (AAPE) (Kim and Kim 2016), which can be defined as follows

$$\begin{aligned} {\text {AAPE}}_{i, j, k} = \arctan \left( \left| \frac{(f_{i, j, k} - {\hat{f}}_{i, j, k})}{f_{i, j, k}}\right| \right) . \end{aligned}$$
(9)

From Eq. (9), we can compute the error in predicting \({\mathtt{I}}_i(t_k)\). In that way, considering the different scenarios presented in Table 2, our goal will be to compare the output obtained from the null and alternative models; that is, we will plot the errors for scenarios 01 and 02, 03 and 04, etc. Figure 3 shows the AAPEs comparing scenarios 15 and 16. Also, Figures SF9, SF10, SF11, SF12, SF13, SF14, SF15, SF16, SF17, SF18, and SF19 (Supplementary Information) show the other plots for the remaining pairs of corresponding scenarios.

Fig. 3
figure 3

Computed AAPEs for groups 1, 2, and 3 (0–19, 20–59, and 60+, respectively), all cells, and for all k. Scenarios 15 (upper row) and 16 (lower row). Models were fitted with data up to \(t_{49}\) (vertical solid line). The upper row corresponds to the errors for the fitted null model (\({\mathcal {M}}_0\)), and the lower for the fitted alternative model (\({\mathcal {M}}_1\))

Full size image

From Fig. 3 (and all others in the Supplementary Information), we can see that, although the estimated intensity functions (and therefore, the estimated number of infected individuals per cell) for the null and alternative models approximate equally well the true process for \(k \le 49\), when making predictions. That is, for \(k > 49\), the null model (\({\mathcal {M}}_0\)) tends to mispredict the process values—if compared to the alternative model (\({\mathcal {M}}_1\)) under the same setting. Also, when the epidemic ends, as we can observe at later times in the EP scenarios, the null model overestimates the number of infectious individuals, while for the alternative model, the estimated \({\mathtt{I}}_i(t_k)\) curve greatly contributes to the correct predictions.

5 Case study

In this section, we model the initial number of COVID-19 cases in Cali, the third-biggest city in Colombia and one of the most populated. The data were provided by the Municipal Public Health Secretary of the cityFootnote 1 and recorded the confirmed COVID-19 cases at an individual-level from 21/01/2020 to 18/06/2020 (Fig. 4, top-left panel). In total, 4,518 unique individuals were observed. The data were collected so that we have access to the initial locations of the infected individuals and their first symptoms dates. We make two assumptions to obtain the infectious curves: (1) all infected individuals will not move while being infected, and (2) the recovery time is assumed to be five days—as suggested by He et al. (2020). Also, as no covariates (e.g., age) were made available, we do not divide the population into different age groups; instead, the \(C_{ij}\) will only have one element (representing the average number of contacts a person of any age has). As in Sect. 4, an estimate for \(C_{ij}\) was retrieved from the COVOID package (Fitzgerald et al. 2020).

Fig. 4
figure 4

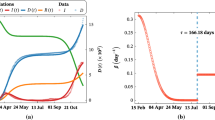
Top-left panel: Map of Cali, Colombia, and 4,518 unique infected (COVID-19) individual locations (red dots) from 21/01/2020 to 18/06/2020. The map also shows the grid used to fit the model. Top-right panel: Estimated \({\mathtt{I}}_i(t_k)\) curve. The model was fitted with data up to \(t_{129}\) (vertical dashed line). Bottom-left panel: Computed AAPEs based on the fitted Null Model (\({\mathcal {M}}_0\)) for all \(t_k\). The model was fitted with data up to \(t_{129}\) (vertical solid line). Bottom-right panel: Computed AAPEs based on the fitted Alternative Model (\({\mathcal {M}}_1\)) for all \(t_k\). The model was fitted with data up to \(t_{129}\) (vertical solid line)

Full size image

Based on the approach described in Sects. 3 and 4.2, we fit the null (\({\mathcal {M}}_0\)) and alternative (\({\mathcal {M}}_1\)) models to the data. In particular, we rely on Eqs. (7) and (8), respectively, for describing the intensity processes. In this regard, \(\lambda _{0, i}({\textbf{u}}; t_k)\) is set as proportional to the population density in Cali (WorldPop 2020), \({\mathtt{I}}_i(t_k)\) is obtained from the temporal modeling approach described in Sect. 3.1 (Fig. 4, top-right panel), and \(\zeta _i({\textbf{u}}; t_k)\) is defined according to the IID structure introduced in Sect. 3.2. Finally, we use data from 21/01/2020 to 29/05/2020 (130 days) to fit the model and make predictions for the remaining period (20 days). The error in predicting the future number of infected individuals in all 131 cells is computed based on Eq. (9).

Figure 4 (bottom-left and bottom-right panels) shows the computed errors for both fitted null and alternative models. From these plots, we can see that, for all \(t_k\), such that \(k \le 139\), the two models have similar performance; in fact, the Null Model seems to perform better than the Alternative Model. This happens because the SIR model is too rigid and fails to capture the shape of the true infectious curve for the observed time points (Fig. 4, top-right panel). The estimated SIR parameters are presented in Table ST4 (Supplementary Information). However, when forecasting, the information provided by the SIR step improves the quality (for the AAPE) of the Alternative Model, making it better than the Null Model for almost all cells.

6 Discussion

Infectious disease modeling is essential to understand epidemic dynamics in the past and predict its future. By doing this, researchers can identify highly infectious areas, and decision-makers can use such information to choose where and when to focus their resources. In this paper, we have introduced a new infectious disease modeling approach for spatio-temporal point pattern data. In particular, we proposed a two-step framework for modeling data on the infectious locations at each time for different age groups. Firstly, we used a compartment SIR model with contact matrix information to characterize the epidemic dynamics in time. Secondly, we incorporated this information into the mean component of a Cox process that models the epidemic dynamics in space-time for all groups. By doing this, provided that the temporal model in the first step is “reasonably well specified”, the spatio-temporal modeling is also guaranteed to produce reasonable estimates in space for time points also in the future.

Regarding implementation and always under a Bayesian framework, for the temporal and spatio-temporal models, we used RStan and R-INLA, respectively. Using these tools, we can be very flexible in the model specification without considerably changing the implemented procedure. For instance, in the temporal-modeling step, many different models for counting data could have been employed to describe the number of infected individuals over time. We believe that extending our approach in that direction may result in more flexible and, therefore, more valuable methods. Also, for the spatio-temporal modeling step, notice that the log-Gaussian Cox process (LGCP) is easily implemented in R-INLA, so we can take advantage of its speed when fitting the corresponding models. Alternatively, other models, e.g., self-exciting point processes (Reinhart 2018), may replace the LGCP in such a framework.

Aiming to assess our model, we first analyzed a combination of real and simulated data. From that, we have seen that when we compare the null model with our two-step modeling framework for space-time, our approach provides similar results for past values but performs much better for time points in the future (for the AAPE). In other words, by describing the mean component of our spatial Cox process through the estimated \({\mathtt{I}}_i(t_k)\) curves from the compartment modeling step, we gain information about the epidemic dynamics and make better predictions. Second, we analyzed a COVID-19 data set. In particular, by modeling the number of infectious cases in space and time according to our approach, we observed that, even though the temporal component was not very well fitted to the observed count data, the spatio-temporal modeling still benefited from such estimates when making predictions for almost all cells.

However, our approach also has limitations. For instance, recall that the proposed framework assumes a SIR model with age structure to model the number of infected individuals over time and a log-Gaussian Cox process to model spatio-temporal patterns. These assumptions may not be appropriate for all scenarios, and other structures can be included depending on the application. For instance, although we focused on the SIR model with age groups throughout this work, other temporal models could have been used as the first step of our modeling approach. Even non-compartment models can be implemented—however, the main advantage of the SIR model in predicting future times well (assuming that the assumptions hold) might be lost. Also, note that the presented model uses infected individuals’ exact locations and times. These data may be challenging to obtain or present underreporting issues. However, if good quality data is available, our model can help us to understand infectious diseases spreading and contribute to health policies.

Thus, in future work, we might be interested in extending such an approach for a broader scenario, relaxing some of the assumptions made in Sect. 2.1, or proposing alternative ways to deal with the challenge of obtaining point pattern data for the infected individuals. Finally, to increase our model performance, we could add covariates that are known to affect infection transmission and structures that consider reporting delays and underreporting. This might help us to describe the underlying intensity processes better and obtain smaller errors when forecasting.