Dissecting innovative trend analysis

Abstract

Investigating the nature of trends in time series is one of the most common analyses performed in hydro-climate research. However, trend analysis is also widely abused and misused, often overlooking its underlying assumptions, which prevent its application to certain types of data. A mechanistic application of graphical diagnostics and statistical hypothesis tests for deterministic trends available in ready-to-use software can result in misleading conclusions. This problem is exacerbated by the existence of questionable methodologies that lack a sound theoretical basis. As a paradigmatic example, we consider the so-called Şen’s ‘innovative’ trend analysis (ITA) and the corresponding formal trend tests. Reviewing each element of ITA, we show that (1) ITA diagrams are equivalent to well-known two-sample quantile-quantile (q–q) plots; (2) when applied to finite-size samples, ITA diagrams do not enable the type of trend analysis that it is supposed to do; (3) the expression of ITA confidence intervals quantifying the uncertainty of ITA diagrams is mathematically incorrect; and (4) the formulation of the formal tests is also incorrect and their correct version is equivalent to a standard parametric test for the difference between two means. Overall, we show that ITA methodology is affected by sample size, distribution shape, and serial correlation as any parametric technique devised for trend analysis. Therefore, our results call into question the ITA method and the interpretation of the corresponding empirical results reported in the literature.

1 Introduction

Testing trend hypothesis on observed time series is one of the most common exercises reported in the hydro-meteorological literature mainly owing to the interest in detecting possible consequences of human activities on the dynamics of climate and hydrological cycle. Referring to Khaliq et al. (2009) and Bayazit (2015) for an overview of methods, trend analysis usually relies on the application of some statistical hypothesis tests for slowly-varying and/or abrupt changes (e.g. Mann–Kendall (MK), Pettitt, or similar) to summary statistics of hydrological time series (e.g. annual averages, maxima and minima).

However, trend analysis is often performed in a mechanistic way with little attention to the underlying assumptions and the limits of Significance Tests (STs; Cox and Hinkley 1974) for trends. Referring to Wasserstein and Lazar (2016), Wasserstein et al. (2019) and references therein for a thorough discussion on misuse and logical flaws of STs, Serinaldi et al. (2018) attempted to warn practicing hydrologists against a mechanistic use of classical trend tests in the analysis of hydro-climatic time series.

Focusing on practical standpoint, it should be noted that some trend STs suggested in the literature are technically incorrect. An example of these methods is the (still) widely used trend-free prewhitening (TFPW) technique (Yue et al. 2002), whose formal flaws are discussed by Serinaldi and Kilsby (2016a). TFPW technical inconsistencies resulted in contrasting empirical results that led to various but incorrect interpretations about the origin/cause of the detected trends (e.g. Khaliq et al. 2009; Kumar et al. 2009; Sagarika et al. 2014; Basarin et al. 2016; Pathak et al. 2016; Tananaev et al. 2016; Xiao et al. 2017). Therefore, the problem of technical flaws is particularly important in this context, as trend analysis is often used to support conclusions concerning the evidence of anthropogenic activity on hydro-climatic processes, and their extensive application (due to their relative simplicity) resulted in a large body of literature supporting this hypothesis, irrespective of the fact that STs are not devised to analyze non-randomized samples coming from non-repeatable experiments such as the majority of hydro-climatic records (Flueck and Brown 1993; von Storch 1999; Greenland et al. 2016; Serinaldi et al. 2018).

Şen’s innovative trend analysis (ITA) (Şen 2012) is one of many techniques proposed to detect deterministic trends in observed time series. This method attracted the attention of analysts as it was introduced with the appealing (but questionable) claim that this technique “does not require restrictive assumptions because now classical approaches including most frequently used Mann–Kendall trend test and Sepeard’s [Spearman’s] rho test. The new methodology is valid whatever the sample size, serial correlation structure of the time series, and non-normal probability distribution functions (PDFs). Although the classical methods require prewhitening prior to their applications, such a procedure is not necessary in the proposed methodology in this paper. The validity of the methodology is presented first through extensive Monte Carlo simulation methods” (Şen 2012). A method that is not affected by sample size, serial correlation and type of distribution surely appears a sort of panacea for trend analysis. However, every statistical method (1) deals with sampling uncertainty and must be sensitive to it, otherwise it would be deterministic, and (2) every statistical analysis relies on weak or strong assumptions (see “Appendix 1”). By the way, Şen (2012) does not report any Monte Carlo simulation despite what is stated in the conclusions of that paper (some Monte Carlo simulations were reported two years later by Şen (2014), and they are discussed below).

Since we were attracted by the apparently amazing properties of ITA and its presentation and justification, we reviewed all the elements and principles of this method, thus performing a so-called neutral (independent) validation/falsification analysis (see e.g. Boulesteix et al. 2018, and references therein). This study reports the results of such a review, showing that ITA diagrams are equivalent to two-sample quantile-quantile (q–q) plots, while ITA formal tests, once corrected for mathematical inconsistencies, reduce to standard parametric tests for the difference between two means, and therefore ITA diagnostics are affected by sample size, serial correlation and type of distribution.

This work is structured as follows. Section 2 introduces the rationale of ITA diagnostic plots and explains that they are simple two-sample q–q plots. We also recall the correct interpretation of these diagrams and show that they are affected by sample size, serial correlation and type of distribution. Section 3 further investigates the effect of serial correlation on ITA, showing that several contradicting statements reported in the literature (Şen 2012, 2014, 2017b) depend on the model used to combine deterministic trends and serial correlation, thus stressing that ITA relies on strong assumptions. In Sect. 4, we revise the formal ST proposed within the ITA framework, and show that it is a standard parametric test for the difference between two means, once the mathematical inconsistencies of the ITA formulas are corrected. Section 5 explains why the ITA confidence intervals (CIs) are incorrect and recalls how to build correct CIs. In Sect. 6, we discuss how the above mentioned inconsistencies affect also some methods and analyses derived from ITA. Conclusions and recommendations are summarized in Sect. 7.

2 Setting the stage: overview of ITA and two-sample quantile-quantile plots

Şen’s ITA comprises a graphical tool and a formal hypothesis test (Şen 2012, 2014, 2017c). The same material with minor changes has then been collected in a book (Şen 2017b), and directly applied by other authors without any independent assessment of its rationale and mathematical formulation (e.g., Cui et al. 2017; Tosunoglu and Kisi 2017; Wu and Qian 2017; Alashan 2018; Caloiero 2018; Caloiero et al. 2018; Güçlü 2018a; Morbidelli et al. 2018; Zhou et al. 2018; Li et al. 2019).

ITA consists of splitting a time series of (even) size n, $\left\{ x_i\right\} _{i=1}^n$, in two halves of size $n'=n''=n/2$, $\mathbf{x }' = \left\{ x_i\right\} _{i=1}^{n/2}$ and $\mathbf{x }'' = \left\{ x_i\right\} _{i=n/2+1}^{n}$, sorting them in ascending order (i.e. computing the order statistics $x'_{(i)}$ and $x''_{(i)}$, $i=1,\ldots ,n/2$), and then plotting the pairs of sorted values, $(x'_{(i)},x''_{(i)})$, $i=1,\ldots ,n/2$, against each other. The foregoing procedure is the same used to draw two-sample q–q plots widely applied to check whether two samples (with the same size) have the same distribution (Wilk and Gnanadesikan 1968). In our case, the two samples are the first and second halves of a time series. Even though the interpretation of two-sample q–q plots is well-known and reported in introductory handbooks of applied statistics, it is worth recalling basic properties to support the subsequent discussion. Referring to Fig. 1 and assuming that $\mathbf{x }'$ follows a standard Gaussian distribution, (1) a shift with respect to the 1:1 line corresponds to a shift in the first moment, $\varDelta \mu = \mu ''-\mu '$ (or location parameter of the underlying theoretical distribution), where $\mu '$ and $\mu ''$ are the first moments of $\mathbf{x }'$ and $\mathbf{x }''$, respectively; (2) q–q plots showing approximately linear patterns with slopes different from 1:1 denote discrepancies in the second moment (or scale parameter); (3) J-shaped q–q plots denote differences in the skewness; and (4) S-shape configurations correspond to discrepancies in terms of kurtosis (e.g. Bennett et al. 2013). Of course, there are also other possible patterns depending on the nature of the distribution support (e.g. upper/lower bounded), and the presence of outliers or mixtures of distributions (see e.g., D’Agostino and Stephens 1986, pp. 24–57). Despite this variety of possible cases, in Şen’s interpretation, whatever departure from the 1:1 line is considered as an exclusive sign of the presence of a deterministic trend. We stress again that both ITA and two-sample q–q plots take two time series (in this specific case the two halves of a single time series), arrange them in ascending order and plot one of these ordered series versus the other one. Therefore, two-sample q–q plots compare the empirical distributions of two series and do not involve any theoretical distribution. In this respect, it is important to distinguish the general rationale of q–q plots, i.e. comparing two generic distributions, with their standard use for assessing the agreement between the empirical distribution and a theoretical distribution.

Fig. 1

Examples of time series and corresponding two-sample q–q plots where the distributions of $\mathbf{x }'$ and $\mathbf{x }''$ have different properties. a, b${\mathcal {N}} (0,1)$ versus ${\mathcal {N}} (1,1)$ (shift in the mean value but same variance). c, d${\mathcal {N}} (0,1)$ versus ${\mathcal {N}} (0,1.4)$ (same mean but different variance). e, f${\mathcal {N}} (0,1)$ versus ${\mathcal {G}} (0,0.78)$, where ${\mathcal {G}}$ is the Gumbel distribution (same mode and variance but different skewness). g, h${\mathcal {N}} (0,1)$ versus $\mathcal {PE} (0,1,0.9)$, where $\mathcal {PE}$ is the power-exponential distribution (same mean, variance, and skewness but different kurtosis)

Obviously, two-sample q–q plots and therefore ITA diagrams are influenced by the shape of the distribution, serial dependence, and sample size, as these factors influence the uncertainty of the scatter plots of $\mathbf{x }''$ versus $\mathbf{x }'$. A simple Monte Carlo simulation can help visualizing these issues. We consider two distributions, standard Gaussian (${\mathcal {N}} (0,1)$) and standard exponential (${\mathcal {E}} (1)$), different samples sizes $n=\left\{ 50,100,500,1000\right\}$, and different dependence structures corresponding to first-order autoregressive (AR(1)) processes with parameter $\rho _1=\left\{ 0, 0.5, 0.7, 0.9 \right\}$. For each combination of parameters, 1000 samples are simulated and ITA diagrams (i.e. two-sample q–q plots) are drawn. For ${\mathcal {N}} (0,1)$, Fig. 2 shows that (1) the scattering of ITA patterns around the 1:1 line decreases as the sample size increases, (2) the scattering and the range of simulated values increase as the serial dependence increases because of variance-inflation effect and reduction of effective size, and (3) the scattering is larger around the tails because of the larger uncertainty of extreme values. Figure 3 shows how the shape of the ensemble of ITA plots changes when the distribution is no longer bell-shaped and symmetric (e.g. Gaussian) but right skewed (e.g. exponential). In particular, as ${\mathcal {E}} (1)$ is lower bounded, the variability in the lower tail becomes null (Fig. 3). The same remarks hold for the upper tail when the distribution is left skewed and/or upper bounded, mutatis mutandis.

Fig. 2

ITA plots (two-sample q–q plots) for samples drawn from an AR(1) process with parameter $\rho _1 \in \left\{ 0,0.5,0.7,0.9\right\}$, ${\mathcal {N}}(0,1)$ marginal distribution, and sample size $n \in \left\{ 50,100,500,1000\right\}$. The diagrams show the dependence of sampling uncertainty of ITA plots on $\rho _1$ and n. The case $\rho _1 = 0$ corresponds to the i/id process

Fig. 3

As for Fig. 2 but with ${\mathcal {E}} (1)$ marginal distribution

These examples highlight that it is rather difficult to obtain ITA plots laying on the 1:1 line even if the two halves of time series, $\mathbf{x }'$ and $\mathbf{x }''$, are drawn from the same distribution without introducing any deterministic trend. Although these properties are well known, according to Şen (2014), ITA diagnostic plot (i.e. the two-sample q–q plot) “does not require any assumption, and it can be applied in cases of serial dependence, non-normal data distribution, and small sample lengths”. The following arguments support this statement (Şen 2012): “the basis of the approach rests on the fact that if two time series areidenticalto each other, their plot against each other shows scatter of points along 1:1 (45$^\circ$) line on the Cartesian coordinate system... Whatever the time series are whether trend free or with monotonic trends, all fall on the 1:1 line when plotted. There is no distinction whether the time series are non-normally distributed, having small sample lengths, or possess serial correlations”. This statement, which is true for two identical finite-size time series (i.e. perfectly correlated data) or infinite-size sequences (i.e. when dealing with population properties), is then transposed tout court to the case of the two halves of the same finite-size time series, overlooking that $\mathbf{x }'$ and $\mathbf{x }''$ are never identical, and their fluctuations and the corresponding ITA plot patterns depend on sample size, serial correlation, and shape of the parent distribution, as shown in Figs. 2 and 3.

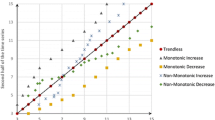
The above remarks strongly influence the interpretation of ITA plots. According to Şen (2012), if the patterns fall above (below) the 1:1 line they denote the presence of monotonic increasing (decreasing) deterministic trend, while mixed patterns (i.e., part of the points laying above the 1:1 line and part below) can be related to non-monotonic trends. However, for finite-size samples, the location of the ITA plot with respect to the 1:1 line is neither necessary nor sufficient condition to make conclusions about the presence of deterministic trends. In fact, departures from the 1:1 line can be related to sampling fluctuations, autocorrelation, and shape of distribution without any deterministic trends. On the other hand, the ITA plot can lie on the 1:1 line when there is a deterministic trend resulting in identical distributions of $\mathbf{x }'$ and $\mathbf{x }''$. Figure 4a–d shows that the ITA plots of $\mathbf{x }'$ and $\mathbf{x }''$ can depart from the 1:1 line for samples drawn from a stationary AR(1) process (with $\rho _1 = 0.95$) or a sequence resulting from independent and identically distributed (i/id) random variables with standard Gumbel distribution (${\mathcal {G}}(0,1)$). Conversely, an increasing linear trend in $\mathbf{x }'$ followed by a decreasing linear trend in $\mathbf{x }''$ can yield indistinguishable sorted samples (Fig. 4e–f). The same can hold true for combinations of linear and nonlinear trends (Fig. 4g–h). The comparison of Fig. 4b and j highlights that almost indistinguishable ITA plot patterns can result from finite-size time series characterized by true deterministic linear trends and sequences from a serially correlated stationary process, thus preventing any discrimination based on this type of diagrams.

Fig. 4

Counter examples showing how ITA plots (two-sample q–q plots) can be misleading in drawing conclusions about the presence of deterministic trends. a, b Time series and ITA plots of a time series of size $n=1000$ simulated from an AR(1) process with $\rho _1=0.95$. c, d Similar to panels (a) and (b) but for an i/id process with ${\mathcal {G}}(0,1)$ marginal distribution. e, f Time series and ITA plots of a sequence resulting from the superposition of an i/id process with ${\mathcal {N}}(0,1)$ marginal distribution and a non-monotonic deterministic trend linearly increasing (decreasing) in the first (second) half of the time series. g, h Similar to panels (e) and (f) but with a S-shaped nonlinear increasing trend in the first half of the time series. i, j Similar to panels (e) and (f) but with a linear decreasing trend spanning the entire time series. Panels (b) and (d) show cases where ITA plots (seem to) indicate departures from the expected 1:1 line even if no deterministic trend is in place. Panels (f) and (h) show that (almost) perfect alignment along the 1:1 line is possible when non-monotonic trends are in place. Panel (j) shows that true deterministic linear trends can yield ITA plots almost indistinguishable from those corresponding to serially correlated time series from a stationary process reported in panel (b). See text for further discussion

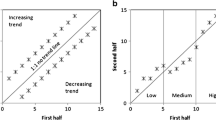
The diagrams discussed above suggest another remark. Şen (2012) suggests splitting the ITA plot in three areas corresponding to low, medium, and high values, and therefore studying each subset, interpreting departures from the 1:1 line as possible trends in each class of values. This procedure has three problems, at least: (1) the identification of the three areas in the ITA plot is arbitrary; (2) splitting the samples generally means performing the analysis on very few data points (Figure 4 in Şen (2012) shows examples where the clusters of high quantiles include 3–7 data points); and more importantly (3) Figs. 2, 3, and 4d show that different classes of values (i.e. low, medium and high) exhibit very different departures from the 1:1 line even in cases where there is no ‘trend’, and the magnitude of these discrepancies depends to the shape of the generating distribution and further increases as the (possible) serial correlation increases and the sample size decreases. Therefore, interpreting departures of few points from the 1:1 line without considering that such a type of diagrams are affected by serial dependence, shape of the distribution and sample size, is generally misleading. We further discuss the role of the sampling uncertainty and its proper quantification in Sect. 5.

3 Effects of autocorrelation: challenging the principle of non-contradiction

According to Şen (2012), ITA should be unaffected by serial correlation. However, Şen (2017b, pp. 194–196) shows that the shift of the ITA patterns from the 1:1 line increases as the correlation increases for fixed (linear) trend values. Şen (2017b, p. 196) also provides a table showing the values of the shift corresponding to a set of linear trend slopes $\beta$ and lag-1 autocorrelation $\rho _1$, claiming that such a “table can be used to determine the magnitude of monotonic trend in any time series provided that the serial correlation coefficient and the slope on the square area template are determined”. In order to better understand the apparently contradictory statements about dependence or independence of ITA from serial dependence, we repeat the Monte Carlo experiments presented in Şen’s original works with the same setting.

In this section, we show that some of the statements about sensitivity of ITA to autocorrelation refer to two different models, one of which is not mentioned in the ITA literature, while conclusions about the ability of ITA to recognize the sign of serial correlation result from incorrect diagrams. We further stress that ITA results are strongly dependent on the model used to merge deterministic trends and serial correlation.

3.1 Are ITA diagrams independent of autocorrelation? Distinguishing population and finite-size sample properties

According to Şen (2017b, pp. 192–193), the effect of serial correlation is studied by superimposing a sequence drawn from a (discrete in time) trend-free stationary first-order autoregressive process with parameter $\rho _1$ to a linear trend with slope parameter $\beta$. This model (hereinafter, M1) is widely used in the literature on trends (Zhang et al. 2000; Wang and Swail 2001; Yue and Wang 2002; Zhang and Zwiers 2004) and reads as follows:

$$\begin{aligned} {\left\{ \begin{array}{ll} y_t = x_t + \beta t\\ x_t = \rho _1 x_{t-1} + \varepsilon _t, \end{array}\right. } \end{aligned}$$

(1)

where $\varepsilon _t$ is an i/id standard Gaussian process. Following Şen (2017b), we simulated single time series of size $n=10,000$ for various combinations of values of $\beta$ and $\rho _1$. Comparing the simulations for $\rho _1$ equal to zero (independence) and 0.9 [Figures 5.15 and 5.16 in Şen (2017b)], Şen (2017b) concluded that “Comparison of Figs. 5.15 and 5.16 indicate that whether the time series is independent or dependent, there is no difference in the square area procedure and as long as the basic time series has a monotonic trend, the appearance of the two-halves sorted magnitude plots will appear along$45^{\circ }$straight-lines without any distinction. This statement alleviates the drawback of the MK trend test, which requires independent data”.

Figure 5j and t reproduce the original ITA plot of figures 5.15 and 5.16 in Şen (2017b) [note that the figure 5.15 is identical to figure 3 in Şen (2014)]. Time series corresponding to each ITA plot are reported in panels 5a–i and k–s. Figure 5t shows that the ITA plots corresponding to $\rho _1 =0.9$ cover a wider range of values (especially for low $\beta$ values) and are less aligned along the 1:1 line, thus showing some irregular fluctuations when compared with the ITA plots in Fig. 5j (with $\rho _1 =0$). These differences can appear small and negligible; however, they are the effect of the variance inflation due to the serial correlation and seem to be small only because the analysis refers to relatively long time series. In fact, for $n = 10,000$ and $\beta = 0.003$, the signal-to-noise ratio, here defined as the ratio between the variance of the signal (i.e. the linear trend line) and that of the autoregressive noise, $r_{\rm SN} = \sigma ^2_{\rm S}/\sigma ^2_{\rm N}$, is 75 for $\rho _1 =0$ and $\cong 14$ for $\rho _1 =0.9$. Although $r_{\rm SN}$ dramatically decreases as $\rho _1$ increases, it is still high because the amplitude of the deterministic trend dominates the amplitude of the stochastic component. For $n=10,000$, even though values of $\beta$ equal to e.g. 0.003 seem small in terms of absolute value, they correspond to a shift of 30 units between the beginning and the end of the time series, while the range of the superposed noise is one order of magnitude smaller. Therefore, from a theoretical point of view, serial correlation does not change the magnitude of $\beta$ under M1.

Fig. 5

Simulations from model M1 with varying trend slope $\beta$. The diagrams highlight the effect of serial correlation and sample size on the uncertainty of ITA plots (two-sample q–q plots)

However, in real world analysis, where $r_{\rm SN}$ is usually much smaller, serial correlation affects the ITA plot patterns, and therefore the estimation of the true values of $\beta$. Let us consider shorter time series of size $n=1000$ (Fig. 5u–ad). For $n=1000$ and $\rho _1 =0.9$, the fluctuations related to the deterministic trend and stochastic component have the same order of magnitude, thus concealing the linear trend. The lack of alignment of the ITA plots and their mutual overlapping in Fig. 5ad are the affect of the variance inflation due to the serial correlation. In other words, serial correlation increases the variance of the stochastic part, thus concealing the linear pattern of the deterministic component. The latter becomes evident only if the length of the time series is long enough, so that the deterministic shift is much larger than the range of the stochastic fluctuations.

To summarize, from a theoretical point of view (i.e. looking at the population properties), the structure of M1 implies that $\beta$ does not change with $\rho _1$; however, from an operational standpoint (i.e. considering finite-size sample properties), for combinations of $\beta$, $\rho _1$ and n yielding sequences with small $r_{\rm SN}$, the empirical ITA plots fluctuate, introducing departures from the expected patterns that can be incorrectly interpreted as systematic trends.

3.2 Do ITA diagrams depend on autocorrelation? The role of model assumptions

As discussed above, the theoretical ITA plot patterns (say, for $n \rightarrow \infty$) are invariant to serial correlation for the model M1. However, in a further discussion, Şen (2017b) [pp. 194–198 and figures 5.19, 5.20 and 5.21, which are identical to figures 4, 5 and 6 in Şen (2014)] concludes that “as the absolute value of the serial correlation coefficient increases the trend representing lines get away from 1:1 (45$^\circ$) straight-line basic line”. Therefore, does the slope of the trend line, and thus the shift in the ITA plot, depend or not on serial correlation from a theoretical point of view? To answer this question, we reproduced Figures 5.19 and 5.20 reported by Şen (2017b, p. 197) in Fig. 6a–b. The patterns of time series and ITA plots shown in Fig. 6a–b cannot be produced by model M1 (Eq. 1) as they correspond to the following one (hereinafter, M2):

$$\begin{aligned} y_t = \rho _1 y_{t-1} + \beta t + \varepsilon _t. \end{aligned}$$

(2)

Figure 6c–d shows results for M1 (with fixed $\beta$ and varying $\rho _1$) for the sake of comparison. Model M2 is not mentioned in any Şen’s works, which exclusively refer to M1. The fundamental missing information in Şen (2014, 2017b) is that the results concerning the (theoretical) dependence of trend slope on serial correlation (actually $\rho _1$), are not general but model-dependent, and cannot be mechanistically applied to real-world data for at least two reasons: (1) observed data do not come for sure from such models, which are only approximations, and (2) the interpretation of ITA diagrams depends on the assumed model. Therefore, $\beta$ is theoretically dependent of $\rho _1$ only under model M2.

Fig. 6

a, b Time series and ITA plots (two-sample q–q plots) of time series simulated from model M2 with fixed $\beta$ and varying $\rho _1$. c, d Similar to panels (a) and (b) but for time series drawn from model M1

Using Monte Carlo simulations, Şen (2017b) studied the relationship between $\beta$, $\rho _1$ and the shift of the ITA plots from the 1:1 line [Figure 5.18 and table 5.1 in Şen (2017b)], concluding that “This table [5.1] can be used to determine the magnitude of monotonic trend in any time series provided that the serial correlation coefficient and the slope on the square area template are determined”. However, this statement holds true only for time series coming from model M2 (which is not mentioned in any Şen’s work), while it does not if we assume M1 or other models combining linear trends and correlated process in different ways.

Moreover, the properties of model M2 are well known (van Giersbergen 2005; Hamed 2009). In particular, recalling that $n'=n/2$, under M2, the theoretical relationships between $\beta$, $\rho _1$ and the shift of the ITA plots from the 1:1 line is (see “Appendix 2”)

$$\begin{aligned} \varDelta \mu \cong \dfrac{\beta n'}{1-\rho _1}. \end{aligned}$$

(3)

Equation (3) yields the exact values corresponding to the approximate Monte Carlo $\varDelta \mu$ reported in table 5.1 of Şen (2017b) for $n=1000$ (see Table 1 for a comparison) and shows that $\varDelta \mu$ depends on n. Therefore, Şen’s numerical results are already known from theoretical standpoint and are not general, as they strictly depend on sample size and the specific model assumed to describe the observed time series. Neglecting these issues and claiming that those results are valid with no assumptions or restrictions can lead to incorrect conclusions.

Table 1 Effective trend slope of time series drawn from model M2 for $n=1000$

3.3 Can ITA diagrams reveal the sign of autocorrelation? A matter of incorrect labeling

Another apparent property of ITA diagrams should be their capability to distinguish between positive and negative correlation (Şen 2017b, p. 194). This conclusion is based on Şen’s interpretation of Figure 5.17 of Şen (2017b), which is reproduced in Fig. 7a to support our discussion. The ITA plots in Fig. 7a can be obtained only if the corresponding time series look like those shown in Fig. 7b. This would mean that negative values of $\rho _1$ should be able to invert the sign of the observed trend, which is not possible. In fact, for model M2, the mean depends on time according to the relationship $\mu _t \cong \frac{\beta t}{1-\rho _1}$ (Eq. 14 in “Appendix 2”). Therefore, the effective trend of the process is greater (smaller) than $\beta$ for positive (negative) values of $\rho _1$, but it is always positive with a minimum equal to $\beta /2$ for $\rho _1 = -1$. For model M1, $\beta$ does not depend on $\rho _1$. Figure 7c–f shows correct ITA plots and time series corresponding to models M1 and M2 for fixed $\beta$ and varying $\rho _1$, and confirms the foregoing theoretical remarks.

Fig. 7

Effect of negative serial correlation. Panel (a) reproduces ITA plots (two-sample q–q plots) of figure 5.17 in Şen (2017b), while panel (b) shows the corresponding time series (note that variability around the trend lines appears very small because of the high signal-to-noise ratio). Panels (c) and (d) depict the correct results for the model M2. e, d Similar to panels (c) and (d) but for the model M1

Figure 5.17 in Şen (2017b) (here, Fig. 7a), which is the support of Şen’s conclusions, does not report results for fixed $\beta$ and varying $\rho _1$. Actually, it refers to model M2 with positive $\rho _1$ values and $\beta \in \left\{ -0.09, 0.09\right\}$, which is indeed similar to Fig. 6a for $\beta \in \left\{ -0.009, 0.009\right\}$. Therefore, the supposed ability of ITA plots to highlight positive and negative correlation results from a speculation around a diagram with incorrect labels [Figure 5.17 in Şen (2017b)] that does not show what is supposed to do.

4 ITA test for trends: mathematical inconsistencies and equivalence to standard parametric test for the difference between two means

The ITA plots come with a formal ST (Şen 2017c). Similar to ITA diagrams, this ST is introduced claiming that it “has non-parametric basis without any restrictive assumption, and its application is rather simple with the concept of sub-series comparisons that are extracted from the main time series... The suggested methodology is valid even for time series with serial correlation structure” (Şen 2017c). In this section, we double check Şen’s test formalism and verify if this test is really assumption-free.

The first (rather strong) assumption is that this formal test only deals with linear trends, while true rank-based (‘non-parametric’) tests, such as MK, deal with more general monotonic trends. In fact, Şen’s test aims at establishing the statistical significance of the slope parameter $\beta$ of a linear trend $x = \alpha + \beta t$ (Şen 2017b, p.  200), where $\beta$ is estimated by the sampling averages, $m'$ and $m''$, of $\mathbf{x }'$ and $\mathbf{x }''$, respectively (Şen 2017b, p.  201)

$$\begin{aligned} {\hat{\beta }} = \dfrac{2(m'' - m')}{n} = \dfrac{m'' - m'}{\dfrac{3n}{4} - \dfrac{n}{4}} = \dfrac{m'' - m'}{\tau '' - \tau '}, \end{aligned}$$

(4)

where $\tau ' = \dfrac{n}{4}$ and $\tau '' = \dfrac{3n}{4}$ are the averages of the sequences of time steps $\left\{ 1,2,\ldots ,n/2\right\}$ and $\left\{ n/2+1,n/2+2,\ldots ,n\right\}$ in the first and second half of the time series $\left\{ x_1,\ldots ,x_n\right\}$.

Generally, there is neither empirical nor theoretical argument justifying the supposed evolution of natural processes according to straight lines (see Serinaldi et al. 2018, for a discussion). Moreover, systematic deviations of ITA diagrams from the 1:1 line do not necessarily correspond to linear trends. In fact, sequences of observations exhibiting a monotonic trend in the mean (or whatever central tendency index) yield a shift in ITA plots, which therefore do not allow for distinguishing linear or nonlinear trends in the original time series. Figure 8 shows that time series with linear trend, abrupt change or S-shaped trend can yield indistinguishable ITA plots. Since ITA plots cannot provide any evidence about the existence of a linear trend, testing the statistical significance of $\beta$ is arbitrary.

Fig. 8

Time series and ITA plots (two-sample q–q plots) for three different types of monotonic deterministic trends (linear (a), step-wise (c), and nonlinear S-shaped (e)). Panels (b), (d) and (f) show that different trends can correspond to similar ITA plots

Let $\mu '$ and $\mu ''$ be the population means corresponding to the sample means $m'$ and $m''$. Testing $\beta = \frac{2(\mu '' - \mu ')}{n}$ means testing the difference between two means, and ITA plots do not play any role in this formulation. In fact, Şen test is only the most common test for the difference between two means for two samples of the same size n/2, where the two populations are Gaussian with known and identical standard deviation $\sigma '= \sigma ''= \sigma$. This test is reported in every statistical handbook as one of the simplest examples of ST, and it is also fully parametric and (obviously) affected from serial dependence.

Under the null hypothesis, $H_0 : \beta =0$, Şen’s test assumes that the following test statistic has standard Gaussian distribution

$$\begin{aligned} t_{\rm ITA}= & {} \dfrac{{\hat{\beta }} - \beta }{\sigma _{{\hat{\beta }}}} = \dfrac{2}{n} \dfrac{(m'' - m') - (\mu ' - \mu '')}{\sigma _{m'' - m'}} \nonumber \\= & {} \dfrac{2}{n} \dfrac{\varDelta m - \varDelta \mu }{\sigma _{\varDelta m}} = \dfrac{2}{n} t_{\rm standard}, \end{aligned}$$

(5)

in which $\text {E}[{\hat{\beta }}] = \beta =0$ and

$$\begin{aligned} \sigma ^2_{{\hat{\beta }}} = \text {Var}[{\hat{\beta }}] = \dfrac{8}{n^2} \dfrac{\sigma ^2}{n}(1-\rho _{m' m''}), \end{aligned}$$

(6)

where $\rho _{m' m''}$ is the cross-correlation coefficient of the sample means $m'$ and $m''$, while $t_{\rm standard}$ is discussed later.

Despite the claims about the lack of assumptions of this test, it actually implies a number of strong assumptions:

• 1. The test statistic in Eq. (5) is normally distributed if the sampling distribution of $m'$ and $m''$ is Gaussian. For small samples, this property requires that $\mathbf{x }'$ and $\mathbf{x }''$ are normally distributed as well. This assumption can be relaxed for large samples sizes ($n \rightarrow \infty$) according to the central limit theorem (Mood et al. 1974, p.  234-236), bearing in mind that the convergence of the sampling distribution of $m'$ and $m''$ to Gaussian can be very slow when the distribution of the parent process X is skewed and/or heavy tailed.

• 2. The derivation of the variance in Eq. (6) requires that the two samples $\mathbf{x }'$ and $\mathbf{x }''$ are homoscedastic (Şen 2017b, p. 205), and the variance of the parent process, $\sigma ^2$, is known. In fact, if $\sigma ^2$ is unknown and estimated from the sample standard deviations $s'$ and $s''$, the test statistic is no longer normally distributed but follows a Student distribution with $n-2$ degrees of freedom (Mood et al. 1974, p. 432-435).

These assumptions are the same characterizing the standard test for differences between two means (using known variances) relying on the test statistic $t_{\rm standard}$ (Kottegoda and Rosso 2008, pp. 252), which is identical to Şen’s $t_{\rm ITA}$ up to the factor 2/n (Eq. 5). Note that the expression of $t_{\rm ITA}$ also neglects that the variances are actually unknown and estimated on the data. The direct comparison of the two methods also reveals that Eq. (5) is incorrect, as it assumes that $\sigma _{m'} = \sigma _{m''} = \sigma /\sqrt{n}$ (see Şen (2017b) p. 205 and Şen (2017c) p. 946), while the variances of the sample means over samples of size n/2 are equal to $\sigma /\sqrt{n/2}$, resulting in the corrected expression

$$\begin{aligned} \sigma ^2_{{\hat{\beta }}} = \dfrac{16}{n^2} \dfrac{\sigma ^2}{n}(1-\rho _{m' m''}), \end{aligned}$$

(7)

which returns indeed the variance of $t_{\rm standard}$, $4 \sigma ^2 / n$, when we remove the nuisance factor 2/n in Eq. (5) and set $\rho _{m'm''} = 0$. Therefore, Şen’s expression in Eq. (6) underestimates the actual variance of $t_{\rm ITA}$ of a factor two.

Fig. 9

Sampling distributions of the test statistics $t_{\rm s}$ and $t_{\rm standard}$ for the i/id process and AR(1) process with $\rho _1=0.9$. KR[2008] = Kottegoda and Rosso (2008)

However, the main theoretical inconsistency in Şen’s formulation is not the foregoing multiplicative factor but the interpretation and estimation of $\rho _{m'm''}$. At its first appearance in the derivation of $\sigma ^2_{{\hat{\beta }}}$, $\rho _{m'm''}$ is correctly introduced as the “cross-correlation coefficient between the ascendingly sorted two-halves–arithmetic averages” (Şen 2017b, p. 205). However, in the subsequent paragraph, Şen (2017b, p. 205) states that “the most significant point in the application of this formulation is that the cross-correlation is between the two-sorted half time series”. This statement is also repeated by Şen (2017c, p.  246), and this definition is used in the applications, resulting in very high correlation values (reflecting the alignment of the points in the ITA diagram), and thus very low values of $\sigma ^2_{{\hat{\beta }}}$ [see lines 6 and 7 in table 5.3 of Şen (2017b)]. Şen (2017b) describes these values saying that “one of the important points in this table is high cross-correlation values in row 6 [of Table 5.3], because they are calculated depending on the ordered sequence in each half series”.

Firstly, it is (or should be) obvious that the sample means of the two sub-series $\mathbf{x }'$ and $\mathbf{x }''$ do not change if the two samples are sorted or not, and thus Şen’s test statistic is not related in any way to ITA plots. Moreover, if the data are uncorrelated, the sample means $m'$ and $m''$ are uncorrelated as well, i.e. $\rho _{m'm''} = 0$. Secondly, the correlation $\rho _{m'm''}$ between the sample means $m'$ and $m''$ of the two samples $\mathbf{x }'$ and $\mathbf{x }''$is not the correlation $\rho _{\mathbf{x }'_{(i)} \mathbf{x }''_{(i)}}$ between the pairs of sorted values, $(x'_{(i)},x''_{(i)})$, $i=1,\ldots ,n/2$, reported in ITA plots. A reductio ad absurdum argument can prove the theoretical inconsistency of switching $\rho _{m'm''}$ with $\rho _{\mathbf{x }'_{(i)} \mathbf{x }''_{(i)}}$. Under i/id conditions (i.e. lack of trend and persistence), for large n and neglecting the sampling uncertainty, the points of the ITA plot are approximately well aligned along the 1:1 line and $\rho _{\mathbf{x }'_{(i)} \mathbf{x }''_{(i)}} \cong 1$. Replacing $\rho _{m'm''}$ with $\rho _{\mathbf{x }'_{(i)} \mathbf{x }''_{(i)}}$ into Eq. (7), it follows that $\sigma ^2_{{\hat{\beta }}} \cong 0$ as $(1-\rho _{\mathbf{x }'_{(i)} \mathbf{x }''_{(i)}}) \cong 0$. In this case, every empirical estimate of $t_{\rm ITA}$ that is not almost exactly equal to zero indicates a significant trend. In other words, $\sigma ^2_{{\hat{\beta }}} \cong 0$ with or without the presence of trends. On the other hand, under i/id, the estimates of the sample means from two samples are uncorrelated with $\rho _{m'm''} \cong 0$ (the values of $\rho _{m'm''}$ under i/id and serial correlation are further investigated by Monte Carlo simulations in “Appendix 3”). Therefore, $\rho _{m'm''} \cong 0 \ne 1 \cong \rho _{\mathbf{x }'_{(i)} \mathbf{x }''_{(i)}}$. The unjustified (and theoretically unjustifiable) replacement of $\rho _{m'm''}$ with $\rho _{\mathbf{x }'_{(i)} \mathbf{x }''_{(i)}}$ strongly deflates the variance of the test statistics, thus leading to an incorrect and dramatically high rate of rejection of the null hypothesis when it is true, i.e. an effective level of significance much higher than the desired target level (see Monte Carlo simulations and additional discussion in “Appendix 4”).

5 Theoretical inconsistency of confidence intervals of ITA plots and corresponding significance test

Even though ITA plots are introduced as diagnostic tools that are not affected by sample size, serial correlation, and distributional assumptions, Şen (2017b, pp. 314–317) suggests quantifying their sampling uncertainty by confidence intervals (CIs) describing the expected fluctuations of the pairs of order statistics $(x'_{(i)},x''_{(i)})$ around the 1:1 line in the ITA plots under the assumption of no trend. As usual, the distribution used to build CIs is also used to introduce a formal ST on the significance of the departures of ITA plots from the 1:1 line (Şen 2017b, pp. 297–304). We note some logical contradiction of suggesting statistical tests (as those in Sect. 4) and CIs to complement a method that is supposed to be inherently free from sample size effects. However, this contradiction can be due to the lack of distinction between population and sample properties in the original description of these methods. Nonetheless, Şen (2017b, pp. 297–304) introduced such a test and CIs as follows.

5.1 Reviewing ITA test for departures from the 1:1 line

Under the assumption of no trend (in the central tendency measures such as the mean), we expect that the difference between the sample means of $\mathbf{x }'$ and $\mathbf{x }''$ has expected value $\text {E}[\mu '' - \mu '] = 0$. We also expect that the pairs of order statistics $(x'_{(i)},x''_{(i)})$ in the ITA plots are aligned along the 1:1 line with small departures. Even though we have shown in Sect. 2 that the latter condition is neither necessary nor sufficient in empirical analysis of finite-size samples, such departures are quantified by the “square root of square deviation summation (SRSDS),$s_{\rm d}$, between the two half series scatter points from the 1:1 line as”

$$\begin{aligned} s_{\rm d} = \sqrt{\dfrac{1}{n}\sum ^{n/2}_{i=1}(X_i - X_{n/2+1})^2}. \end{aligned}$$

(8)

Therefore, according to Şen (2017b, p. 303), “in order to convert this information into an objective form the division of the mean difference, ($m_2-m_1$) [i.e., $(m'' - m')$ in the present notation] , by the SRSDS in Eq. 7.16 [i.e. Eq. (8) in this paper], leads to the definition of trend test statistic,$t_{\rm s}$, as”

$$\begin{aligned} t_{\rm s} = \dfrac{m'' - m'}{s_{\rm d}}. \end{aligned}$$

(9)

Finally, Şen (2017b, p. 303) provides the following interpretation: “The small values of this test statistics,$t_{\rm s}$, imply that there is trend and variability, which is regarded as the null hypothesis,$H_{\rm o}$. On the contrary, the big values corresponds to the alternative hypothesis,$H_{\rm a}$, where there is no trend or variability. Theoretically,$t_{\rm s}$has zero mean and unit variance, and hence, the standard normal pdf can be used for the significance test”.

Focusing on the analytical and conceptual inconsistencies, firstly but least, (1) $X_{n/2+1}$ should be $X_{n/2+i}$; (2) using this correction, $X_{i}$ and $X_{n/2+i}$ should be $x_{(i)}$ and $x_{(n/2+i)}$ as Eq. (8) refers to differences between corresponding order statistics; (3) the factor 1/n should be 2/n because the sum is taken over n/2 terms; and (4) the suggested interpretation is incorrect, as the null hypothesis of ‘no trend’ corresponds to $t_{\rm s}\rightarrow 0$; in fact, if the test statistic in Eq. (9) is standard normal under the null, it means that $(m'' - m') \rightarrow 0$, and this can happen only if $m'' \cong m'$, i.e. if the null hypothesis is ‘no trend’, as usual in standard statistical testing.

Secondly and most important, the statistic $t_{\rm s}$ has neither unit variance nor Gaussian distribution because the expression of the sample variance $s^2_{\rm d}$ is not consistent with the numerator in Eq. (9) and does not provide a valid standardization factor. In fact, generally speaking, formulas yielding standardized statistics with zero mean and unit variance require subtraction of the expected value (here, $\text {E}[\mu '' - \mu '] =\text {E}[\varDelta \mu ]= 0$) and division by the standard deviation of the variable of interest, which is $\varDelta m = (m'' - m')$ in the present case. However, the standard deviation of $\varDelta m$ is not $s_{\rm d}$ but $\sigma _{\varDelta m}$ in Eq. (5). Using $\sigma _{\varDelta m}$, $t_{\rm s}$ becomes identical to the statistic $t_{\rm original}$ in Eq. (5), which is actually distributed as ${\mathcal {N}}(0,1)$, thus revealing that also this test is once again nothing but the standard test for the difference between two means reported in every and handbook of applied statistics (see e.g. Kottegoda and Rosso 2008, pp. 252–253). The corrected statistic $t_{\rm s}$ is also identical to $t_{\rm ITA}$ up to the factor 2/n. Moreover, such tests rely on several assumptions and depend on the preliminary knowledge (or lack of knowledge) of the population variances and serial dependence. In fact, the expression of $\sigma _{\varDelta m}$ assumes different forms according to the specific case at hand. For example, under serial independence, homoscedasticity (i.e. $\sigma '= \sigma ''= \sigma$), and same sample size $n'=n''=n/2$, if $\sigma$ is known (not estimated from the same sample), we have (see e.g. Kottegoda and Rosso 2008, pp. 252) $\sigma _{\varDelta m} = \frac{2}{\sqrt{n}}\sigma$, while

$$\begin{aligned} \sigma _{\varDelta m} = \sqrt{\frac{2}{{n}} (s'^2+s''^2)} \end{aligned}$$

(10)

if the population standard deviations $\sigma '$ and $\sigma ''$ are unknown but equal, and $s'$ and $s''$ are their sample version. Under serial dependence, $\sigma _{\varDelta m}$ should be multiplied by a correction factor, $f_{\rm corr}$, to account for the variance inflation effects yielding

$$\begin{aligned} {\left\{ \begin{array}{ll} \sigma ^*_{\varDelta m} = \sigma _{\varDelta m}\sqrt{1+\left( \dfrac{n}{2}-1\right) {\bar{\rho }}} = \sigma _{\varDelta m}\, f_{\rm corr} \\ {\bar{\rho }} = \dfrac{\sum \sum _{j\ne l}\rho _{ij}}{\dfrac{n}{2}\left( \dfrac{n}{2}-1\right) } \end{array}\right. } \end{aligned}$$

(11)

where ${\bar{\rho }}$ is the average of the off-diagonal elements of the correlation matrix of n/2 variables, and $\rho _{ij} = \text{Corr }[X_i,X_j]$ denotes the pairwise correlation of $X_i$ and $X_j$ (Matalas and Langbein 1962).

Some Monte Carlo experiments further clarify the above criticisms. We simulated 1000 time series of size $n=100$ from the i/id model and an AR(1) process with $\rho _1=0.9$. For each series, we computed $t_{\rm s}$ according to Eqs. (8) and (9) (corresponding to Eqs. 7.16 and 7.17 in Şen (2017b, p. 303)), and $t_{\rm standard}$ using the variances in Eq. (10) for the i/id case and Eq. (11) for the AR(1) process. Figure 9 shows that the distribution of ${t_{\rm s}}$ is far from being ${\mathcal {N}}(0,1)$ and its shape depends on the serial correlation as expected, while the empirical probability density function of $t_{\rm original}$ is close to ${\mathcal {N}}(0,1)$ for both processes, thus confirming the effectiveness of the correction factor $f_{\rm corr}$. Note that different values of n and $\rho _1$ yield similar results (not shown). Since Şen’s ${t_{\rm s}}$ is not Gaussian and depends on serial correlation, it follows that ${\mathcal {N}}(0,1)$ cannot be used to compute valid critical values to perform a statistical test.

5.2 Reviewing the CIs of ITA diagrams

Even though $s_{\rm d}$ cannot be used to describe the variance of $\varDelta m$, thus making the test based on ${t_{\rm s}}$ invalid, one can think that $s_{\rm d}$ can be applied at least to build CIs around the 1:1 line. Indeed, in principle $s_{\rm d}$ should describe the variance of the fluctuations of the order statistics of $\mathbf{x }''$ with respect to those of $\mathbf{x }'$ (after correcting the expression in Eq. (8) for the formal errors mentioned above). Therefore, if such fluctuations are approximately Gaussian, we can define confidence limits from the distribution ${\mathcal {N}}(0,s^2_{\rm d})$. However, this is not correct either, because each order statistic appearing in the ITA plot has its own distribution, which is a beta of the form $F_{X_{(i)}}={\mathcal {B}} (F_X(x_{(i)}); \nu p,\nu (1-p))$, where $F_X$ is the parent distribution of X, $\nu =n'+1$, and $p \in [1/\nu ,n'/\nu ]$ (Stigler 1977; Hutson 1999; Nadarajah and Gupta 2004; Serinaldi 2009). Therefore, the ensemble of fluctuations of a set of order statistics does not necessarily converge to a Gaussian distribution and this hypothetical distribution does not describe the uncertainty of each order statistic, meaning that we cannot define a unique CI with constant width for all data points reported in ITA plots. A proper Monte Carlo simulation reported in “Appendix 5” can provide a visual assessment of these remarks.

This behavior is further illustrated in Fig. 10 where constant-width ITA CIs (at the 95% confidence level) are reported along with true point-wise CIs for order statistics computed by two different methods: (1) from simulated samples, and (2) by using the theoretical distribution $F_{X_{(i)}}$. Both methods yield almost identical CIs summarizing the different degree of uncertainty characterizing extreme and non-extreme order statistics. Especially for skewed distributions (i.e. exponential and Gumbel), the upper tails of the ITA plots might substantially depart from the expected 1:1 line and fall outside Şen’s (supposed) CIs. Therefore, splitting the ITA plot in three areas corresponding to low, medium, and high values, and thus studying their alignment with 1:1 line separately, as suggested by Şen (2012), is generally misleading as this suggestion overlooks the different uncertainty affecting central and extreme order statistics related to sample size and shape of the parent distribution.

Fig. 10

Comparison of Şen’s CIs and true point-wise CIs of order statistics for the three models ${\mathcal {N}}(0,1)$, ${\mathcal {E}}(1)$, and ${\mathcal {G}}(0,1)$. True CIs are computed via Monte Carlo simulation (‘MC CIs’) and theoretical formulas (‘OS CIs’) at the 95% confidence level. CI = confidence interval

6 Building on the sand: ITA follow-ups

Taking the correctness of ITA for granted without any independent preliminary check led not only to mechanistic applications of ITA diagnostics but also to attempts of improvement whose outcome should be interpreted according to the foregoing discussion. For example, Güçlü (2018b) suggested the so-called multiple ITA, consisting of splitting the time series of size n in k (= 3,4,...) non-overlapping sub-sets of size $\left\lfloor n/k\right\rfloor$, and then applying ITA to subsequent pairs of sub-sets, thus obtaining $k-1$ ITA diagrams (e.g., for $k=3$, there are two diagrams of the pairs of sorted values $(x'_{(i)},x''_{(i)})$ and $(x''_{(i)},x'''_{(i)})$, $i=1,\ldots ,\left\lfloor n/3\right\rfloor$). Such a procedure increases the uncertainty of each ITA plot, as the diagrams rely on smaller samples. Moreover, this segmentation has a two-fold negative effect: (1) it can conceal possible serial correlation, which is already under-represented for instance in the usually short hydro-climate time series (Serinaldi and Kilsby 2016b; Iliopoulou and Koutsoyiannis 2019); and (2) it emphasizes spurious trends resulting from (concealed) serial correlation, thus leading to incorrect conclusions about the presence of deterministic trends. Generally speaking, focusing on small subsets always reveals some trend since the straight lines usually fitted to time series have never zero slope; however, such trends are statistically and physically less and less significant because they rely on a smaller and smaller amount of information.

McCuen (2018) explored the problem of statistical significance investigating how much deviation from the 1:1 line can be expected because of sampling uncertainty. McCuen’s approach consists of testing the slope of the zero-intercept regression line fitted to the ITA plot, i.e. $\mathbf{x }''_{(\bullet )} = \beta _{\rm M} \mathbf{x }'_{(\bullet )}$, where $\mathbf{x }'_{(\bullet )} = \{x'_{(i)} \}_{i=1}^{n/2}$ and $\mathbf{x }''_{(\bullet )} = \{x''_{(i)}\}_{i=1}^{n/2}$. Using Monte Carlo simulations, McCuen (2018) computed the critical values of $\beta _{\rm M}$ under the null hypothesis $H_0 : \beta _{\rm M} =1$ (and i/id and $X\sim {\mathcal {N}}(0,1)$), and concluded that these critical values (obtained for a Gaussian distribution) hold approximately true for uniformly distributed data but not for data following an exponential distribution. These results are expected if we recognize the identity of ITA plots and two-sample q–q plots, and recall their properties discussed in Sect. 2. Firstly, $\beta _{\rm M} \gtrless 1$ does not necessarily correspond to changes/trends but can be related to fluctuations in the second moment (or scale parameter), i.e. possible heteroskedasticity [see Sect. 2, Fig. 1, and examples in D’Agostino and Stephens (1986, pp. 24–57)]. Secondly, McCuen’s critical values do not hold for the exponential distribution because this distribution is right skewed and lower bounded to zero. Therefore, under i/id (no trends), the lower part of the ITA plots always converges to zero (see Fig. 3), the bundle of ITA plots resulting from sampling uncertainty has a fan shape, and each ITA plot is generally well fitted by zero-intercept regression line with $\beta _{\rm M} \ne 1$. In other words, for the exponential distribution, $\beta _{\rm M}$ estimates are almost always different from the unity even if data are i/id, and this does not depend on trends but on the shape of the distribution. Similar remarks hold for other skewed families. Parallelism with the 1:1 line under sampling uncertainty holds approximately only for symmetric distributions such as the uniform or Gaussian (see e.g. Fig. 2) mentioned by McCuen (2018). Therefore, a closer preliminary consideration of the nature and meaning of ITA plots reveals that testing the slope of a zero-intercept regression line is not an optimal strategy to obtain a general purpose test identifying deviations from i/id (in terms of step changes and/or trend in the mean levels) via ITA plots.

Similar remarks hold for other works as well. For example, Şen (2017a) used ITA to analyze time series pre-processed by the so-called over-whitening procedure, without accounting for the effect of sample size and distribution shape on ITA diagrams. In other cases, the term ITA was used even if the methodology is weakly if not related to ITA construction. For example, Şen et al. (2019) proposed the so-called ‘Innovative Polygon Trend Analysis’ (IPTA) that is based on a diagram plotting the summary statistics of the two halves of the twelve monthly series $\left\{ x_{j,i}\right\}$, $j=1,\ldots ,12$ and $i=1,\ldots ,n$. For instance, focusing on the mean values m, IPTA diagrams report the twelve points $m'_j$ versus $m''_j$, where $m'_j$ and $m''_j$ denote the average values of the first and second half of the observed monthly series. In this case, according to Şen et al. (2019), the presence of a possible trend for a specific month should be based on a single point in IPTA diagrams, which however provide only a visualization of the differences $\varDelta m_j = (m''_j - m'_j)$ and do not add any additional information compared with $\varDelta m_j$. On the other hand, as for the original ITA diagrams, IPTA interpretation overlooks the effect of sample size, distribution shape, and serial correlation on the sample differences $\varDelta m_j$ and their departures from the expected value zero (under ‘no trend’ assumption). We also stress that $\varDelta m_j$ are routinely analyzed by existing standard tests for the difference between two means discussed in Sect. 4 and 5.1, accounting for the above mentioned factors as well as the additional effect of multiple testing (e.g. Katz and Brown 1991; Wilks 2006).

These studies show the possible negative consequences of taking the validity of new techniques for granted without performing a necessary assessment against benchmark and/or challenging conditions. Especially when new methods promise paramount results under minimal or no assumptions, these techniques should be carefully validated/falsified against the supposed conditions that they should be independent of, and these neutral validation studies should be performed by independent experts (other than the developers) to avoid biases in favor of the new methods (Boulesteix et al. 2018). Moreover, the seemingly widespread difficulty to distinguish names and their meaning (Klemeš 1986), and thus recognizing that different names refer to the same (often known) concept, exacerbates the proliferation of questionable methods.

7 Conclusions

When dealing with observations of complex hydro-climatic processes, whose dynamics are not fully known, statistical techniques play a key role to retrieve and summarize information, and enable analysis and prediction (Cramér 1946, pp. 146–148) (see also Shmueli 2010). They are often the only feasible approach to get insights, and therefore are often abused and misused as well. Even though the problem of misusing statistics is not new and is widely documented in the applied statistical literature, it is exacerbated when supposed ‘innovative’ techniques are developed overlooking basic literature, elementary principles of statistical inference, and necessary careful checks under a reasonable spectrum of different (and possibly challenging) controlled conditions.

The lack of independent validation is mainly due to the fact that the so-called neutral comparison and validation studies may be time consuming and difficult to both organize and perform (Boulesteix et al. 2018). They also require the involvement of authors with enough experience, and are often more difficult to publish as “most high-ranking statistical journals mainly focus on the development of new methods and on innovative applications... As a consequence of the lack of comparison studies, end-users’ decisions for or against application of particular methods are often consciously or subconsciously driven by arguments that are to some extent independent of the performance of the method, such as the charisma and marketing strategy of its developers, its use in similar previous studies, the method’s fancy name that is easy to remember when heard at a conference, or the availability of user-friendly software” (Boulesteix et al. 2018). In this study, we used Şen’s ITA as a paradigmatic example (among many others) involving all these concerns, and performed a neutral validation study to independently check theoretical basis, methodological aspects, mathematical formulation, and consequent interpretation of ITA diagnostic diagrams and formal tests for trend detection.

Referring to the main text for the detailed discussion of the results of our inquiry, we showed that this method

• Cannot discriminate between deterministic trends and spurious trends resulting for instance from serial dependence, when it is applied to finite-size samples (i.e. in real-world applications);

• Overlooks the existing literature, thus neglecting the equivalence of ITA plots and well-known two-sample q–q plots and their intepretation;

• Is characterized by extensive mathematical inconsistencies affecting the formulation of ITA statistical tests. Once these theoretical inconsistencies are corrected, ITA tests are equivalent to well-known classical parametric tests for the difference between two means reported in standard handbooks of applied statistics;

• Contradicts the basic principles of statistical inference, as it is supposed to be free from any assumption while its finite-sample properties strongly depend on sample size and characteristics of the underlying data generating process, such as the shape of the marginal distributions and particularly the autocorrelation.

Overall, ITA suffers from a number of theoretical inconsistencies affecting its derivation, formulas and interpretation. Thus, this study shows the importance of avoiding mechanistic application of new methods taking them for granted, and performing neutral validation/falsification analysis to recognize possible methodological problems affecting new methodologies. Therefore, we recommend to reconsider ITA tools (once corrected for mathematical inconsistencies) in light of their equivalence to existing techniques, thus recognizing their actual purpose, correct interpretation, advantages, disadvantages, and limits. As for the TFPW method mentioned in the introduction, empirical results obtained by ITA should be called into question and double checked.

As a more general recommendation to end-users, we suggest bearing in mind the very general principles of statistical inference and mathematical modeling well synthesized for instance by Cramér (1946), Aitken (1947), von Storch and Zwiers (2003), Papoulis (1991), Morrison (2008) and Shmueli (2010) and summarized in “Appendix 1”. We also suggest carefully checking every new technique before using it to study real-world data. Such a cautionary approach can help avoiding misleading conclusions, which are often used as a support decision making, thus causing (costly) errors in design and planning.

Appendices

Appendix 1

Proposing methodologies that should be model-free, applicable with no assumptions, and unaffected by the sample size, and thus uncertainty-free, contradicts the basic principles of statistical science. Aitken (1947, pp. 2–3) well summarized such principles recalling that every science relies on three main stages:

• 1. Examination of data collected in a particular field of inquiry to disclose elements of regularity suggesting a law or laws. This is the stage of inductive synthesis (see also Cramér 1946, pp. 141–144).

• 2. Expression of these laws, if possible, in the form of logical axioms such as those characterizing the Euclidean geometry or Newtonian mechanics. This is the stage of deductive synthesis and relies on the methods of logic and mathematics, which are used to develop the consequences of the axioms, producing an ensemble of theorems or propositions. In statistics, this pure branch consists of the framework provided by probability and statistical mathematics. When the discrepancies between theory and facts are too great to be explained in some way, observations invalidate the applicability of the axioms, and a new set of axioms should be found for the description and explanation of the investigated phenomena. However, “these axioms and the deductions based on them would still have an abstract validity, as a logical structure of propositions exempt from self-contradiction” (see also Cramér 1946, pp. 145–146).

• 3. Interpretation of the abstract functions, equations, constants, etc., “which occur in the pure formulation, as measures and measurable relations of actual phenomena. This interpretative stage constitutes the applied branch of the science” (see also Cramér 1946, pp. 146–148).

The foregoing principles are fully general and well-known in applied disciplines as well. Specializing them in the statistical context, Papoulis (1991, p. 4) stresses that “In the application of probability to real problems, the following steps must be clearly distinguished

• 1. Step 1 (physical) We determine by an inexact process the probabilities${\mathbb {P}} [{\mathcal {A}}_i]$of certain events${\mathcal {A}}_i$...

• 2. Step 2 (conceptual) We assume that probabilities satisfy certain axioms, and by deductive reasoning we determine fromthe probabilities${\mathbb {P}} [{\mathcal {A}}_i]$of certain events${\mathcal {A}}_i$the probabilities${\mathbb {P}} [{\mathcal {B}}_i]$of certain events${\mathcal {B}}_i$...

• 3. Step 3 (physical) We make a physicalpredictionbased on the numbers${\mathbb {P}} [{\mathcal {B}}_i]$so obtained”.

Likewise, in the context of modeling dynamic systems, Morrison (2008, p. 7) states “The next hurdle [to get over in undergraduate mathematics] is the differences among observed reality, mathematical models, and computational realizations of mathematical models. Even a lot of accomplished scientists are not clear on these points... learning to cope with three things makes up the basics of a liberal scientific education: facts, abstractions, and the comparison of facts with abstractions... Understanding and ultimately research occurs only when facts are reduced to abstraction, the abstractions manipulated to make predictions, and the prediction compared with new facts”. The practical use of a mathematical theory is not restricted to prediction but includes description and analysis (Shmueli 2010). In particular, concerning the descriptive purposes, “a large set of empirical data may, with the aid of the theory, be reduced to a relatively small number of of characteristics which represent, in a condensed form, the relevant information supplied by the data” (Cramér 1946, p. 147). Therefore, every statistical analysis, including descriptive statistics, relies on a mathematical theory with its axioms, assumptions and theorems. For example, while we can numerically compute the sample mean for whatever sequence of real numbers, it represents an estimate of a corresponding population mean only under the assumption that the observations come from a sequence of identically distributed random variables, i.e. for stationary and ergodic random processes. As every statistical analysis relies on some assumptions, this explains why there cannot be diagnostic plots or supposed innovative methods that are assumption-free. This is also well known in statistics applied to climatology. von Storch and Zwiers (2003, p. 69) state:

• 1. “A statistical model is adopted that supposedly describes both the stochastic characteristics of the observed process and the properties of the method of observation. It is important to be aware of the models implicit in the chosen statistical method and the constraints those models necessarily impose on the extraction and interpretation of information.”

• 2. “The observations are analysed in the context of the adopted statistical model.”

Sometimes, some assumptions can be relaxed. For example, “non-parametric approaches to statistical inference are distinguished from parametric methods in that the distributional assumption is replaced by something more general. For example, instead of assuming that data come from a distribution having a specific form, such as the normal distribution, it might be assumed that the distribution is unimodal and symmetric.” (von Storch and Zwiers 2003, p. 76). However, “While they allow us to relax the distributional assumption needed for parametric statistical inference, these procedures rely more heavily upon the sampling assumptions than do parametric procedures” (von Storch and Zwiers 2003, p. 76). In other words, statistical inference does not allow for ‘free lunches’ and what we gain in terms of flexibility by relaxing some assumption is paid in terms of power of discriminating among different options. It follows that the primary inherent conceptual flaw of ITA is to present it as something which is presumed to be valid albeit it clearly contradicts basic scientific principles.

Appendix 2

For the model M2, we have

$$\begin{aligned}&\text {E}[x_t] = \rho _1 \text {E}[x_{t-1}] + \text {E}[\beta t] + \text {E}[\varepsilon _t] \end{aligned}$$

(12)

$$\begin{aligned}&\mu _t= \rho _1 \mu _{t-1} + \beta t + 0. \end{aligned}$$

(13)

Since we can often assume $\mu _{t-1} \cong \mu _{t}$ for $\beta \ll 1$, it follows

$$\begin{aligned} \mu _t \cong \dfrac{\beta t }{1-\rho _1}. \end{aligned}$$

(14)

Therefore

$$\begin{aligned} \varDelta \mu= & {} \mu '' -\mu ' = \mu _{\frac{3n}{4}} - \mu _{\frac{n}{4}} \cong \dfrac{\beta \left( \dfrac{3n}{4} - \dfrac{n}{4}\right) }{1-\rho _1} \nonumber \\= & {} \dfrac{\beta \dfrac{n}{2}}{1-\rho _1} = \dfrac{\beta n'}{1-\rho _1}. \end{aligned}$$

(15)

Appendix 3

To show the correlation between the means in two samples, we simulated 5000 time series with size $n=100$ from three different processes: (1) i/id with standard Gaussian distribution, i.e. $y_t = \epsilon _t$ with $\epsilon \sim {\mathcal {N}}(0,1)$, (2) i/id process with superimposed linear trend ($y_t = \beta t + \epsilon _t$ with $\beta = 0.1$ and $\epsilon \sim {\mathcal {N}}(0,1)$), and (3) a discrete-time AR(1) process with parameter $\rho _1 = 0.95$ ($y_t = \rho _1 y_{t-1} + \epsilon _t$ with $\epsilon \sim {\mathcal {N}}(0,1)$). We computed the means of the two halves of each time series, thus obtaining 5000 pairs $(m', m'')$ and drew the scatter plots of these estimates (Fig. 11). These diagrams describe the empirical joint density functions of $m'$ and $m''$ and show that such sample means are uncorrelated for the first two models ($\rho = 0.02$ and -0.03, respectively), while relatively weak correlation ($\rho = 0.28$) emerges only for highly correlated AR(1) processes ($\rho$ assumes values close to zero for $\rho _1 \le 0.8$, which still denotes remarkable serial correlation). The marginal distributions of $m'$ and $m''$ are close to Gaussian (not shown) with standard deviations close to the expected theoretical values, namely $0.14 \cong \sqrt{\frac{2}{n}} \sigma$ for the first two models and $2.25 \cong \sqrt{\frac{2}{n (1-\rho ^2_1)}\left[ 1+(\frac{n}{2}-1) {\bar{\rho }}\right] } \sigma$ for the AR(1) model, where $\sigma = 1$ and ${\bar{\rho }}$ is the average of the off-diagonal elements of the correlation matrix of n/2 variables, i.e. ${\bar{\rho }} = \frac{\sum \sum _{j\ne l}\rho _{ij}}{\frac{n}{2}(\frac{n}{2}-1)}$, in which $\rho _{ij} = \text{ Corr }[X_i,X_j]$ denotes the pairwise correlation of $X_i$ and $X_j$ (Matalas and Langbein 1962).

Fig. 11

Sampling joint distribution of $m'$ and $m''$ for the i/id process (a), i/id with superimposed linear trend (b), and AR(1) process with $\rho _1=0.95$ (c)

Appendix 4

In order to show the effect of switching $\rho _{m'm''}$ and $\rho _{\mathbf{x }'_{(i)} \mathbf{x }''_{(i)}}$ on the significance of the two-mean tests, we simulated 1000 time series of size $n \in \left\{ 20,40,60,80,100,150, 200, 250 \right\}$ from two processes: (1) an AR(1) process with $\rho _1$ ranging between 0 and 0.9 by 0.1 steps, and (2) a fractional Gaussian noise (fGn) with Hurst parameter $H \in \left\{ 0.5, 0.55,\ldots ,0.95 \right\}$. The time series are kept trend-free to check the effect of the autocorrelation of the parent processes on the effective rejection rate of the tests (applied at the 5% nominal significance level). Note that the AR(1) and fGn processes with $\rho _1 = 0$ and $H = 0.5$, respectively, yield the i/id process, for which the effective significance level is expected to be equal to the nominal level. We compared the Şen test with the standard tests for two means with known or unknown variances. Figure 12 shows that the Şen test always yields a rejection rate greater than the 40% for both processes, every degree of serial correlation (including the i/id case), and every sample size. On the other hand, the two standard tests yield effective significance levels that are close the nominal level (5%) under i/id (as expected) and gradually increase because of the variance inflation effect of the increasing serial correlation. These conclusions further stress the importance of performing suitable Monte Carlo analysis and comparisons with other available tests when a new test is proposed, in order to check its properties under the null hypothesis and the effect of assumptions and factors such as serial dependence and sample size.

Fig. 12

Effective significance of three formulations of the hypothesis test for the difference between two means (Şen’s version and standard test with known or unknown standard deviation (SD)). The effect of the serial correlation is shown for AR(1) and fGn processes

Appendix 5

We simulated samples of size $n \in \left\{ 50, 100, 10,000\right\}$ from three different distributions (Gaussian, Exponential, and Gumbel). The smaller sample sizes ($n \in \left\{ 50, 100\right\}$) cover the typical range of hydro-climatic observations such as annual means or maxima, while $n = 10,000$ was chosen to check results for relatively large samples. For each sample, we selected $\mathbf{x }'$ and $\mathbf{x }''$ and then we computed the differences between the order statistics, $d_i = x''_{(i)}-x'_{(i)}$, and their variance by using Şen’s equation and the standard formula for the variance (which is corrected for the errors mentioned in Sect. 5.1). The variances are used to compute the Gaussian quantiles, $\delta _{i}$, corresponding to the empirical frequencies $i/\nu$, under the assumption that $d_i$ values follow a Gaussian distribution. This experiment was repeated $q=1000$ times, and the 1000 sequences of $d_i$ ($\delta _i$) were merged obtaining samples of size $q\cdot \nu$. Such samples allow for building and comparing the sampling distributions of $d_i$ and $\delta _i$. Figure 13 shows that the distributions of $\delta _i$ are generally different from those of $d_i$ irrespective of the formula used to compute the sample variances of $d_i$. As expected, discrepancies depend on the shape of the parent parent distribution of X and they are smaller when $F_X$ is Gaussian. The main reason of these discrepancies is that the distribution of $d_i$ is not unique but depends on the rank of the order statistics. In fact, as already shown in Fig. 2, the uncertainty of ITA plots is generally smaller for central order statistics and larger on the (unbounded) tails.

Fig. 13

Sampling distribution of $d_i = x''_{(i)}-x'_{(i)}$ and corresponding $\delta _{i}$ for three different distributions (${\mathcal {N}}(0,1)$, ${\mathcal {E}}(1)$, and ${\mathcal {G}}(0,1)$) and $n \in \left\{ 50, 100, 10,000\right\}$. Sampling distributions are obtained by empirical distribution from Monte Carlo simulation and from Gaussian distributions with zero mean and standard deviation as for Eq. (8) [i.e. equation 7.16 in Şen (2017b)] and Eq. (10). See text for further details