Rainfall data simulation by hidden Markov model and discrete wavelet transformation

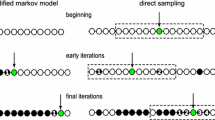
Abstract

In many regions, monthly (or bimonthly) rainfall data can be considered as deterministic while daily rainfall data may be treated as random. As a result, deterministic models may not sufficiently fit the daily data because of the strong stochastic nature, while stochastic models may also not reliably fit into daily rainfall time series because of the deterministic nature at the large scale (i.e. coarse scale). Although there are different approaches for simulating daily rainfall, mixing of deterministic and stochastic models (towards possible representation of both deterministic and stochastic properties) has not hitherto been proposed. An attempt is made in this study to simulate daily rainfall data by utilizing discrete wavelet transformation and hidden Markov model. We use a deterministic model to obtain large-scale data, and a stochastic model to simulate the wavelet tree coefficients. The simulated daily rainfall is obtained by inverse transformation. We then compare the accumulated simulated and accumulated observed data from the Chao Phraya Basin in Thailand. Because of the stochastic nature at the small scale, the simulated daily rainfall on a point to point comparison show deviations with the observed data. However the accumulated simulated data do show some level of agreement with the observed data.

Appendices

Appendix A

The algorithm provided below is used to estimate the parameters in a mixture of Gaussian distributions. It turns out to be a special case of the EM algorithm developed by Dempster, Laird and Rubin (1997). Quick reference could also be made to the book by Hamilton (1994).

Let ${v_{N,1}^{t} (i)}$ be an arbitrary initial guess of v _N,1(i) under the probability rule $\sum\nolimits_{i = 1}^{M} {v_{N,1}^{t} (i)} = 1$ (Here, the superscript t is an iteration counter). For i = 1, 2,…,M, we let

$$ \alpha_{N,1} (i) = v_{N,1}^{t} (i) $$

(35)

and

$$ \beta_{N,1} (i) = \frac{1}{{\sqrt {2\pi } \sigma_{i} }}\exp \left( { - \frac{{D_{N,1}^{2} }}{{2\sigma_{i}^{2} }}} \right). $$

(36)

Then, a new estimation of the probability v _N,1(i) is obtained as:

$$ v_{N,1}^{t + 1} (i) = \frac{{\alpha_{N,1} (i)\beta_{N,1} (i)}}{{\sum\limits_{j = 1}^{M} {\alpha_{N,1} (j)\beta_{N,1} (j)} }} $$

(37)

for i = 1, 2,…,M. The iteration stops when the convergence criterion

$$ \sum\limits_{i = 1}^{M} {\left| {v_{N,1}^{t + 1} (i) - v_{N,1}^{t} (i)} \right|} < \varepsilon $$

(38)

(ε = 1.0E − 6 in this study) is satisfied. Thus the estimation of the probability v _N,1(i) can be obtained.

Appendix B

The EM algorithm for estimating the transition probabilities closely follows the paper by Crouse et al. (1998). The EM algorithm for dependent tree models first appeared in Chow and Liu (1968). Ronen et al. (1995) expanded this work to include the condition that some components of the tree are unobserved. However, the EM steps have been derived only for discrete-valued random variables. Crouse et al. (1998) generalized the algorithm so that it can be applied to the hidden Markov tree models, which are of discrete and continuous valued nodes. We herein slightly modify the algorithm presented in Crouse’s paper, so that some of the parameters (means and variances) are fixed. The steps of the EM algorithm for this model are as follows:

2.1 Initialization

Given arbitrary initial assignments of the transition probabilities T ^t_k,n (i, j) and hidden state probabilities v ^y,t_k,n (i) for different wavelet trees (Here, the superscript t is an iteration counter):

$$T_{k,n}^{t}(i,j): \text{for}\;1 \le i,\;j \le M, k=1,\ldots, N-1,\;\text{and}\;n=2^{N-k-1}+1,\ldots,2^{N-k}.$$

$$\nu_{k,n}^{y,t}(i): \text{for}\;1 \le i \le M,\; k=1,\ldots, N,\;n=2^{N-k-1}+1,\ldots,2^{N-k}\;\text{and}\;y=1,\ldots,Y.$$

under the probability rules: $\sum\nolimits_{i = 1}^{M} {v_{k,n}^{y,t} (i) = 1}$ and $\sum\nolimits_{i = 1}^{M} {T_{k,n}^{t} (i,j)} = 1$ for any choice of j (since for any fixed j, the state variable S ^y_k,n takes a value from {1,…,M}).

2.2 Expectation step (E-step)

For each wavelet tree, i.e. for y = 1,…,Y, we apply the “upward-downward” algorithm:

• A. The upward algorithm

  • 1. Initialization: assign the values of β at the “leaves” of the wavelet trees. For i = 1, 2,…,M and n = 2^N−2 + 1,…,2^N−1, let

    $$ \beta_{1,n}^{y} (i) = \frac{1}{{\sqrt {2\pi } \sigma_{i} }}\exp \left( { - \frac{{(D_{1,n}^{y} )^{2} }}{{2\sigma_{i}^{2} }}} \right) . $$

    (39)

  • 2. Step upward: calculate all the values of β by the following formulas. For k = 2,…,N, n = 2^N−k + 1,…,2^N−k+1, l = 0, 1 and i = 1,…,M,

    $$ \phi_{k - 1,2n - l}^{y} (i) = \sum\limits_{j = 1}^{M} {T_{k - 1,2n - l}^{t} (j,i)\beta_{k - 1,2n - l}^{y} (j)} , $$

    (40)
    $$ \beta_{k,n}^{y} (i) = \frac{1}{{\sqrt {2\pi } \sigma_{i} }}\exp \left( { - \frac{{(D_{k,n}^{y} )^{2} }}{{2\sigma_{i}^{2} }}} \right)\prod\limits_{l = 0}^{1} {\phi_{k - 1,2n - l}^{y} (i)} ,\,{\text{and}}\,{\text{let}} $$

    (41)
    $$ \varphi_{k - 1,2n - l}^{y} (i) = \frac{{\beta_{k,n}^{y} (i)}}{{\phi_{k - 1,2n - l}^{y} (i)}}. $$

    (42)

• B. The downward algorithm

  • 1. Initialization: To get the values of α at the “root” of the wavelet trees, we set for i = 1, 2,…,M

    $$ \alpha_{N,1}^{y} (i) = v_{N,1}^{y,t} (i). $$

    (43)

  • 2. Step downward: obtain the remaining values of α. For k = N,…,2, n = 2^N−k + 1,…,2^N−k+1, l = 0, 1 and i = 1, 2,…,M,

    $$ \alpha_{k - 1,2n - l}^{y} (i) = \sum\limits_{j = 1}^{M} {T_{k - 1,2n - l}^{t} (i,j)\alpha_{k,n}^{y} (j)\varphi_{k - 1,2n - l}^{y} (j)} . $$

    (44)

2.3 Maximization step (M-step)

• A Update the state probabilities in the wavelet trees

• For k = 1,…,N, n = 2^N−k−1 + 1,…,2^N−k and i = 1,…,M, the new iteration is

  $$ v_{k,n}^{y,t + 1} (i) = \frac{{\alpha_{k,n}^{y} (i)\beta_{k,n}^{y} (i)}}{{\sum\limits_{j = 1}^{M} {\alpha_{k,n}^{y} (j)\beta_{k,n}^{y} (j)} }}. $$

  (45)

• B Renew the transition probabilities

  For k = 2,…,N, n = 2^N−k + 1,…,2^N−k+1, l = 0, 1 and i = 1,…,M, the following simplified equation (to facilitate computations) is used:

  $$ T_{k - 1,2n - l}^{t + 1} (i,j) = \frac{1}{Y}\sum\limits_{y = 1}^{Y} {\frac{{T_{k - 1,2n - l}^{t} (i,j)\beta_{k - 1,2n - l}^{y} (i)}}{{\phi_{k - 1,2n - l}^{y} (j)}}} . $$

  (46)

2.4 Convergence checking

• For k = 1,…,N − 1, n = 2^N−k−1 + 1,…,2^N−k and 1 ≤ i, j ≤ M, set

  $$ \varepsilon_{1} = \max \left(\left|T_{k,n}^{t + 1} (i,j) - T_{k,n}^{t} (i,j)\right|\right). $$

  (47)

• For y = 1,…,Y, k = 1,…,N − 1, n = 2^N−k−1 + 1,…,2^N−k and 1 ≤ i ≤ M, set

  $$ \varepsilon_{2} = \max \left(\left|v_{k,n}^{y,t + 1} (i) - v_{k,n}^{y,t} (i)\right|\right). $$

  (48)

• Set ε = max (ε ₁, ε ₂).

  If ε < 1.0E − 6 (convergence criterion), then we STOP the algorithm and set all

  $$ T_{k,n} (i,j) = T_{k,n}^{t + 1} (i,j). $$

  (49)

Otherwise, we need to set $v_{k,n}^{y,t} (i) = v_{k,n}^{y,t + 1} (i)$ and $T_{k,n}^{t} (i,j) = T_{k,n}^{t + 1} (i,j),$ and do the EM algorithm steps again until the convergence criterion is met.