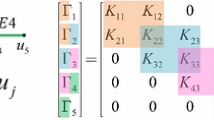Abstract
In nonlinear analysis, performing iterative inverse calculation and nonlinear system construction procedures incurs expensive computational costs. This paper presents an element-wise stiffness evaluation procedure combined with hyper-reduction reduced-order modeling (HE-STEP ROM) method. The proposed approach constructs a non-intrusive reduced-order model based on an element-wise stiffness evaluation procedure (E-STEP) and hyper-reduction methods. Because the E-STEP evaluates nonlinear stiffness coefficients element-by-element using cubic polynomial, numerous number of polynomial variables are required. The number of variables directly affects the computational efficiency of the online and offline stages. Therefore, to enhance efficiency of the online/offline stages, the proposed method employs hyper-reduction method. By applying hyper-reduction, the full stiffness coefficients are approximated from the stiffness coefficients evaluated at a few sampling points. Subsequently, the number of polynomial equations and variables is prominently reduced, and the efficiency of the reduced system increases. The efficiency and accuracy of the proposed approach are validated via several structural dynamic problems with geometric and material nonlinearities.




















Similar content being viewed by others
References
Hoang KC, Fu Y, Song JH (2016) An hp-proper orthogonal decomposition–moving least squares approach for molecular dynamics simulation. Comput Methods Appl Mech Eng 298:548–575
Willcox K, Peraire J (2002) Balanced model reduction via the proper orthogonal decomposition. AIAA journal 40(11):2323–2330
Glaz B, Liu L, Friedmann PP (2010) Reduced-order nonlinear unsteady aerodynamic modeling using a surrogate-based recurrence framework. AIAA journal 48(10):2418–2429
Willcox K, Peraire J, White J (2002) An Arnoldi approach for generation of reduced-order models for turbomachinery. Comput Fluids 31(3):369–389
Glaz B, Friedmann PP, Liu L, Cajigas JG, Bain J, Sankar LN (2013) Reduced-order dynamic stall modeling with swept flow effects using a surrogate-based recurrence framework. AIAA journal 51(4):910–921
Davidsson P, Sandberg G (2006) A reduction method for structure-acoustic and poroelastic-acoustic problems using interface-dependent Lanczos vectors. Comput Methods Appl Mech Eng 195(17–18):1933–1945
Daescu DN, Navon IM (2008) A dual-weighted approach to order reduction in 4DVAR data assimilation. Mon Weather Rev 136(3):1026–1041
Lee J, Cho M (2018) Efficient design optimization strategy for structural dynamic systems using a reduced basis method combined with an equivalent static load. Structural and Multidisciplinary Optimization 58(4):1489–1504
Spiess, H., & Wriggers, P. (2005, December). Reduction methods for FE analysis in nonlinear structural dynamics. In PAMM: Proceedings in Applied Mathematics and Mechanics (Vol. 5, No. 1, pp. 135-136). Berlin: WILEY‐VCH Verlag.
Cho H, Shin S, Kim H, Cho M (2020) Enhanced model-order reduction approach via online adaptation for parametrized nonlinear structural problems. Comput Mech 65(2):331–353
Peherstorfer B, Willcox K (2015) Dynamic data-driven reduced-order models. Comput Methods Appl Mech Eng 291:21–41
Guo M, Hesthaven JS (2018) Reduced order modeling for nonlinear structural analysis using gaussian process regression. Comput Methods Appl Mech Eng 341:807–826
Ghavamian F, Tiso P, Simone A (2017) POD–DEIM model order reduction for strain-softening viscoplasticity. Comput Methods Appl Mech Eng 317:458–479
Baur U, Benner P, Feng L (2014) Model order reduction for linear and nonlinear systems: a system-theoretic perspective. Archives of Computational Methods in Engineering 21(4):331–358
Bai Z (2002) Krylov subspace techniques for reduced-order modeling of large-scale dynamical systems. Applied numerical mathematics 43(1–2):9–44
Sirovich, L. (1987). Turbulence and the dynamics of coherent structures. I. Coherent structures. Quarterly of applied mathematics, 45(3), 561-571.
Chatterjee, A. (2000). An introduction to the proper orthogonal decomposition. Current science, 808-817.
Breuer KS, Sirovich L (1991) The use of the Karhunen-Loeve procedure for the calculation of linear eigenfunctions. J Comput Phys 96(2):277–296
Everson R, Sirovich L (1995) Karhunen-Loeve procedure for gappy data. JOSA A 12(8):1657–1664
Astrid P, Weiland S, Willcox K, Backx T (2008) Missing point estimation in models described by proper orthogonal decomposition. IEEE Trans Autom Control 53(10):2237–2251
Chaturantabut S, Sorensen DC (2010) Nonlinear model reduction via discrete empirical interpolation. SIAM J Sci Comput 32(5):2737–2764
Chaturantabut, S., & Sorensen, D. C. (2009, December). Discrete empirical interpolation for nonlinear model reduction. In Proceedings of the 48 h IEEE Conference on Decision and Control (CDC) held jointly with 2009 28th Chinese Control Conference (pp. 4316-4321). IEEE.
Xiao D, Fang F, Buchan AG, Pain CC, Navon IM, Du J, Hu G (2014) Non-linear model reduction for the Navier-Stokes equations using residual DEIM method. J Comput Phys 263:1–18
Ghavamian F, Tiso P, Simone A (2017) POD–DEIM model order reduction for strain-softening viscoplasticity. Comput Methods Appl Mech Eng 317:458–479
Drmac Z, Saibaba AK (2018) The discrete empirical interpolation method: Canonical structure and formulation in weighted inner product spaces. SIAM Journal on Matrix Analysis and Applications 39(3):1152–1180
Carlberg K, Farhat C, Cortial J, Amsallem D (2013) The GNAT method for nonlinear model reduction: effective implementation and application to computational fluid dynamics and turbulent flows. J Comput Phys 242:623–647
Carlberg K, Barone M, Antil H (2017) Galerkin v. least-squares Petrov-Galerkin projection in nonlinear model reduction. J Comput Phys 330:693–734
Farhat C, Avery P, Chapman T, Cortial J (2014) Dimensional reduction of nonlinear finite element dynamic models with finite rotations and energy-based mesh sampling and weighting for computational efficiency. Int J Numer Meth Eng 98(9):625–662
Farhat C, Chapman T, Avery P (2015) Structure-preserving, stability, and accuracy properties of the energy-conserving sampling and weighting method for the hyper reduction of nonlinear finite element dynamic models. Int J Numer Meth Eng 102(5):1077–1110
Xiao D, Fang F, Pain C, Hu G (2015) Non-intrusive reduced-order modelling of the Navier-Stokes equations based on RBF interpolation. Int J Numer Meth Fluids 79(11):580–595
Xiao D, Yang P, Fang F, Xiang J, Pain CC, Navon IM (2016) Non-intrusive reduced order modelling of fluid–structure interactions. Comput Methods Appl Mech Eng 303:35–54
Muravyov AA, Rizzi SA (2003) Determination of nonlinear stiffness with application to random vibration of geometrically nonlinear structures. Comput Struct 81(15):1513–1523
Capiez-Lernout E, Soize C, Mignolet MP (2014) Post-buckling nonlinear static and dynamical analyses of uncertain cylindrical shells and experimental validation. Comput Methods Appl Mech Eng 271:210–230
Radu, A., Kim, K., Yang, B., & Mignolet, M. (2004, April). Prediction of the dynamic response and fatigue life of panels subjected to thermo-acoustic loading. In 45th AIAA/ASME/ASCE/AHS/ASC structures, structural dynamics & materials conference (p. 1557).
Mignolet MP, Soize C (2008) Stochastic reduced order models for uncertain geometrically nonlinear dynamical systems. Comput Methods Appl Mech Eng 197(45–48):3951–3963
Kim E, Kim H, Cho M (2017) Model order reduction of multibody system dynamics based on stiffness evaluation in the absolute nodal coordinate formulation. Nonlinear Dyn 87(3):1901–1915
Kim E, Cho M (2018) Design of a planar multibody dynamic system with ANCF beam elements based on an element-wise stiffness evaluation procedure. Structural and Multidisciplinary Optimization 58(3):1095–1107
Drmac Z, Gugercin S (2016) A new selection operator for the discrete empirical interpolation method—improved a priori error bound and extensions. SIAM J Sci Comput 38(2):A631–A648
Argaud, J. P., Bouriquet, B., Gong, H., Maday, Y., & Mula, O. (2017). Stabilization of (G) EIM in presence of measurement noise: application to nuclear reactor physics. In Spectral and High Order Methods for Partial Differential Equations ICOSAHOM 2016 (pp. 133-145). Springer, Cham.
Peherstorfer, B., Drmač, Z., & Gugercin, S. (2018). Stabilizing discrete empirical interpolation via randomized and deterministic oversampling. arXiv preprint arXiv:1808.10473.
Ipsen IC, Nadler B (2009) Refined perturbation bounds for eigenvalues of Hermitian and non-Hermitian matrices. SIAM Journal on Matrix Analysis and Applications 31(1):40–53
Lu Y, Blal N, Gravouil A (2018) Space–time POD based computational vademecums for parametric studies: application to thermo-mechanical problems. Advanced Modeling and Simulation in Engineering Sciences 5(1):3
Lu Y, Blal N, Gravouil A (2018) Adaptive sparse grid based HOPGD: Toward a nonintrusive strategy for constructing space-time welding computational vademecum. Int J Numer Meth Eng 114(13):1438–1461
Lu Y, Blal N, Gravouil A (2018) Multi-parametric space-time computational vademecum for parametric studies: Application to real time welding simulations. Finite Elem Anal Des 139:62–72
Kim E, Cho M (2017) Equivalent model construction for a non-linear dynamic system based on an element-wise stiffness evaluation procedure and reduced analysis of the equivalent system. Comput Mech 60(5):709–724
Zimmermann R, Willcox K (2016) An accelerated greedy missing point estimation procedure. SIAM J Sci Comput 38(5):A2827–A2850
Weyl H (1912) Das asymptotische Verteilungsgesetz der Eigenwerte linearer partieller Differentialgleichungen (mit einer Anwendung auf die Theorie der Hohlraumstrahlung). Math Ann 71(4):441–479
Freitag S, Cao BT, Ninić J, Meschke G (2015) Hybrid surrogate modelling for mechanised tunnelling simulations with uncertain data. Int J Reliab Saf 9(2–3):154–173
Cao BT, Freitag S, Meschke G (2016) A hybrid RNN-GPOD surrogate model for real-time settlement predictions in mechanised tunnelling. Advanced Modeling and Simulation in Engineering Sciences 3(1):5
Xiao D, Fang F, Pain CC, Navon IM, Salinas P, Muggeridge A (2015) Non-intrusive reduced order modeling of multi-phase flow in porous media using the POD-RBF method. J Comput Phys 1:1–25
Xiao D, Fang F, Pain CC, Navon IM, Salinas P, Wang Z (2018) Non-intrusive model reduction for a 3D unstructured mesh control volume finite element reservoir model and its application to fluvial channels. Int J Oil Gas Coal Technol 19(3):316–339
Acknowledgements
This work was supported by the National Research Foundation (NRF) of Korea funded by the Korea government (MSIP) (Grant No. 2012R1A3A2048841).
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendices
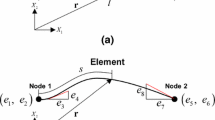
Appendix A : Stiffness evaluation procedure using the least squares method
To clarify the explanation, the displacement combination and stiffness coefficient matrices in Equation (2) are newly defined, as follows:
where Kijkl includes \( K_{ij}^{1} ,K_{ijk}^{2} \), and \( K_{ijkl}^{3} \) in Equation (A1). ujukul is the displacement combination, which includes 1 as its value, and can also be expressed as uj and ujuk (\( u_{j} \cdot 1 \cdot 1 \) and \( u_{j} u_{k} \cdot 1 \)).
If the sample data sets, with internal force and displacement, are collected from the sampling analysis, the internal force model of Equation (A1) for the mth element can be represented as follows:
where m, n, p, and S are the element number, number of degrees of freedom for one element, number of displacement combinations for one element, and quantity of sample data, respectively. \( \tilde{K} \) and \( \tilde{u} \) indicate one combination of Kijkl and ujukul in Equation (A1), respectively. Γm and \( \tilde{\varvec{u}}_{m} \) are the sampled internal force and displacement combination matrix in Equation (A2), respectively. Equation (A2) can be expressed as \( {\varvec{\Gamma}}_{m} = \tilde{\varvec{K}}_{m} \tilde{\varvec{u}}_{m} \). The least squares method is used to evaluate the stiffness coefficient matrix, \( \tilde{\varvec{K}}_{m} \), even if it is not a square matrix. Thus, the stiffness coefficient matrix can be solved for displacement combinations using the least squares method, as follows:
The above process is performed for all elements and a stiffness coefficient suitable for each degree of freedom in the global system is assembled.
Appendix B: GappyPOD + E deterministic sampling strategy
The L2 error of the approximation model satisfies the following equation:
Here, \( \|{\varvec{\Gamma}}^{nl} - {\mathbf{\Omega \Omega }}^{\text{T}} {\varvec{\Gamma}}^{nl}\|_{2} \) affects the approximation quality of the subspace spanned by Ω, and \( \|\left( {{\mathbf{Z}}^{\text{T}} {\varvec{\Omega}}} \right)^{\dag }\|_{2} \) quantifies the effectiveness of the sampling points.
To achieve robustness and minimize the quantity \( \|\left( {{\mathbf{Z}}^{\text{T}} {\varvec{\Omega}}} \right)^{\dag }\|_{2} \) with a small number of sampling points, Refs. [40] proposed the GappyPOD + E (where E is the eigenvector) deterministic sampling strategy. The GappyPOD + E algorithm is based on the lower bound for the smallest eigenvalues of the updated matrix, which was introduced in [41]. The minimization problem is equal to maximizing the smallest eigenvalue of \( {\mathbf{Z}}^{\text{T}} {\varvec{\Omega}} \).
where \( s_{max} \left( {\mathbf{B}} \right) \) and \( s_{min} \left( {\mathbf{B}} \right) \) indicate the largest and smallest singular values of B, respectively. The GappyPOD + E algorithm follows the lower bounds of the smallest eigenvalues to select the sampling points that maximize \( s_{min} \left( {\mathbf{B}} \right) \); this is achieved by leveraging the eigenvector corresponding to the smallest eigenvalue. In this paper, the relevant summary is explained, and a detailed explanation and formulation can be found in Refs. [40]. If the authors add a sampling point, then \( {\mathbf{Z}}_{p + 1}^{T} {\varvec{\Omega}} \in {\mathbb{R}}^{{\left( {p + 1} \right) \times N}} \) becomes
where \( \varvec{\omega}_{ + } \in {\mathbb{R}}^{1 \times N} \) is the row of Ω for the new sampling point. Zimmermann et al. [46] demonstrated that the change in the singular values of \( {\mathbf{Z}}_{p}^{T} {\varvec{\Omega}} \) to \( {\mathbf{Z}}_{p + 1}^{T} {\varvec{\Omega}} \) can be computed using a symmetric rank-one update.
where \( {\mathbf{Z}}_{p}^{T} {\varvec{\Omega}} = \varvec{V}_{p} {\varvec{\Sigma}}_{p} \varvec{W}_{p}^{T} \) is computed using the SVD method. The singular values of \( {\mathbf{Z}}_{p + 1}^{T} {\varvec{\Omega}} \) are calculated by the square roots of the eigenvalues of \( \left( {{\mathbf{Z}}_{p + 1}^{T} {\varvec{\Omega}} } \right)^{T} {\mathbf{Z}}_{p + 1}^{T} {\varvec{\Omega}} \).
where the square roots of the eigenvalues of \( {\varvec{\Lambda}}_{p + 1} \) are singular values of \( {\mathbf{Z}}_{p + 1}^{T} {\varvec{\Omega}} \). Let \( \uplambda_{1}^{{\left( {p + 1} \right)}} , \ldots ,\uplambda_{N}^{{\left( {p + 1} \right)}} \) be the eigenvalues of \( {\varvec{\Lambda}}_{p + 1} \) and \( \uplambda_{1}^{\left( p \right)} , \ldots ,\uplambda_{N}^{\left( p \right)} \) be the eigenvalues of \( {\varvec{\Sigma}}_{p}^{2} \), both arranged in descending order. The GappyPOD + E algorithm aims to select a row Ω that maximizes the smallest eigenvalue \( \uplambda_{N}^{{\left( {p + 1} \right)}} \). From Weyl’s theorem [47], we have \( \uplambda_{N}^{{\left( {p + 1} \right)}} \ge \uplambda_{N}^{\left( p \right)} \), which shows that the additional sampling point will not increase the eigenvalues of \( \|\left( {{\mathbf{Z}}_{p + 1}^{T} {\varvec{\Omega}}} \right)^{\dag }\|_{2} \), compared to the eigenvalues of \( \|\left( {{\mathbf{Z}}_{p}^{T} {\varvec{\Omega}}} \right)^{\dag }\|_{2} \).
In Refs. [40], the lower bounds for the eigenvalues of the updated matrices, for selecting the sampling point to rapidly increase the smallest eigenvalue, are calculated using the following equation:
where\( \bar{\varvec{\omega }}_{ + } = \varvec{W}_{p}^{T}\varvec{\omega}_{ + }^{T} \). \( g = \uplambda_{N - 1}^{\left( p \right)} - \uplambda_{N}^{\left( p \right)} \) indicates the eigengap and \( {\varvec{\Sigma}}_{p}^{2} \) is the diagonal matrix, with diagonal elements sorted in descending order; thus, \( \varvec{z}_{N}^{\left( p \right)} \in {\mathbb{R}}^{N} \) is the Nth canonical unit vector of dimension N. A detailed explanation and derivation of the bound equation can be found in Refs. [40].
Rights and permissions
About this article
Cite this article
Lee, J., Lee, J., Cho, H. et al. Reduced-order modeling of nonlinear structural dynamical systems via element-wise stiffness evaluation procedure combined with hyper-reduction. Comput Mech 67, 523–540 (2021). https://doi.org/10.1007/s00466-020-01946-7
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00466-020-01946-7