Fully coupled simulation of multiple hydraulic fractures to propagate simultaneously from a perforated horizontal wellbore

Abstract

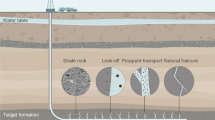
In hydraulic fracturing process in shale rock, multiple fractures perpendicular to a horizontal wellbore are usually driven to propagate simultaneously by the pumping operation. In this paper, a numerical method is developed for the propagation of multiple hydraulic fractures (HFs) by fully coupling the deformation and fracturing of solid formation, fluid flow in fractures, fluid partitioning through a horizontal wellbore and perforation entry loss effect. The extended finite element method (XFEM) is adopted to model arbitrary growth of the fractures. Newton’s iteration is proposed to solve these fully coupled nonlinear equations, which is more efficient comparing to the widely adopted fixed-point iteration in the literatures and avoids the need to impose fluid pressure boundary condition when solving flow equations. A secant iterative method based on the stress intensity factor (SIF) is proposed to capture different propagation velocities of multiple fractures. The numerical results are compared with theoretical solutions in literatures to verify the accuracy of the method. The simultaneous propagation of multiple HFs is simulated by the newly proposed algorithm. The coupled influences of propagation regime, stress interaction, wellbore pressure loss and perforation entry loss on simultaneous propagation of multiple HFs are investigated.

Appendix: Fluid partitioning into two HFs

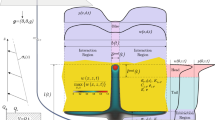
Assume two stationary fractures in linear-elastic solid medium are interconnected by a wellbore with zero friction. The geometry is symmetric with respect to the wellbore. The half lengths are denoted as $l_1$ and $l_2$. Pump inviscid fluid into the two fractures from the wellbore with the given flux $Q_0$. The pressure in the wellbore is uniform with the value $p_w$ and the pressure in each fracture is also uniform with the values of $p_1$ and $p_2$, respectively. The inlet fluxes into the two fractures are denoted as $2q_1$ and $2q_2$. Plane strain assumption is adopted and the heights of the fractures are h. The mass conservation can be given by

$$\begin{aligned} 2hq_1 +2hq_2 =Q_0 \end{aligned}$$

(78)

At the inlets, the entry loss characterized by a coefficient $\varphi _p$ is considered and then

$$\begin{aligned} p_w -p_1= & {} \varphi _p \cdot \left( {2hq_1 } \right) ^{2} \end{aligned}$$

(79)

$$\begin{aligned} p_w -p_2= & {} \varphi _p \cdot \left( {2hq_2 } \right) ^{2} \end{aligned}$$

(80)

Assume there’s no stress interaction effect between the fractures and then from the theoretical solution of a fracture loaded by uniform pressure, the whole volume of the fluid in the fracture is

$$\begin{aligned} V=\frac{2\left( {\kappa +1} \right) \pi hl^{2}}{8\mu }p \end{aligned}$$

(81)

where $\kappa =3-4\nu$ and $\mu =E/{\left[ {2(1+\nu )} \right] }$. Consider the process before the propagation of the fractures and the inlet flow rate for each fracture can be given as

$$\begin{aligned} q_i =\frac{\dot{V}_i }{2h}=c_i \dot{p}_i ,\quad i=1,2 \end{aligned}$$

(82)

where $c_i =\left( {\kappa +1} \right) \pi l_i^2 /\left( {8\mu } \right)$.

The initial conditions are given as

$$\begin{aligned} p_1 (0)=p_2 (0)=p_0 \end{aligned}$$

(83)

Combining Eqs. (78), (79), (80), (82) and (83), we can solve the equations and get the fluxes as

$$\begin{aligned} q_1= & {} \left[ {-\frac{c_1 -c_2 }{2\left( {c_1 +c_2 } \right) }e^{-\eta t}+\frac{c_1 }{c_1 +c_2 }} \right] \cdot \frac{Q_0 }{2h} \end{aligned}$$

(84)

$$\begin{aligned} q_2= & {} \left[ {\frac{c_1 -c_2 }{2\left( {c_1 +c_2 } \right) }e^{-\eta t}+\frac{c_2 }{c_1 +c_2 }} \right] \cdot \frac{Q_0 }{2h} \end{aligned}$$

(85)

where $\eta =\left( {c_1 +c_2 } \right) /\left( {4c_1 c_2 \varphi _p hQ_0 } \right)$. When $t=0$, $q_1 =q_2 =Q_0 /\left( {4h} \right)$ and when $t\rightarrow \infty$, $q_1 =c_1 /\left( {c_1 +c_2 } \right) \cdot Q_0 /\left( {2h} \right)$, $q_2 =c_2 /\left( {c_1 +c_2 } \right) \cdot Q_0 /\left( {2h} \right)$. So we can define the critical time $t_c =1/\eta =4c_1 c_2 \varphi _p hQ_0 /\left( {c_1 +c_2 } \right)$ to characterize the evolution of fluid partitioning.