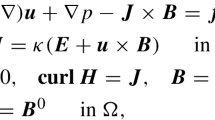Skip to main content
SpringerLink
Log in

Effects of Mesh Motion on the Stability and Convergence of ALE Based Formulations for Moving Boundary Flows

  • Original Paper
  • Published:
Computational Mechanics Aims and scope Submit manuscript

Abstract

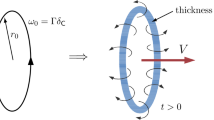
This paper investigates the effects of mesh motion on the stability of fluid-flow equations when written in an Arbitrary Lagrangian–Eulerian frame for solving moving boundary flow problems. Employing the advection-diffusion equation as a model problem we present a mathematical proof of the destabilizing effects induced by an arbitrary mesh motion on the stability and convergence of an otherwise stable scheme. We show that the satisfaction of the so-called geometric conservation laws is essential to the development of an identity that plays a crucial role in establishing stability. We explicitly show that the advection dominated case is susceptible to growth in error because of the motion of the computational grid. To retain the bound on the growth in error, the mesh motion techniques need to account for a domain based constraint that minimizes the relative mesh velocity. Analysis presented in this work can also be extended to the Navier–Stokes equations when written in an ALE frame for FSI problems.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Acosta G, Duran RG (2003) An optimal Pioncaré inequality in L 1 for convex domains. Proc Am Math Soc 132(1):195–202

    Article  MathSciNet  Google Scholar 

  2. Belytschko T, Kennedy JM, Schoeberie DF (1980) Quasi-Eulerian finite element formulation for fluid-structure interaction. ASME J Press Vessel Technol 102:62–69

    Article  Google Scholar 

  3. Bochev P, Gunzburger M, Shadid J (2004) On inf-sup stabilized finite element methods for transient problems. Comput Methods Appl Mech Eng 193(1):1471–1489

    Article  MATH  MathSciNet  Google Scholar 

  4. Brezzi F, Bristeau MO, Franca LP, Mallet M, Roge G (1992) A relationship between stabilized finite element methods and the Galerkin method with bubble functions. Comput Methods Appl Mech Eng 96(1):117–129

    Article  MATH  MathSciNet  Google Scholar 

  5. Brooks AN, Hughes TJR (1982) Streamline upwind/Petrov- formulations for convection dominated flows with particular emphasis on the incompressible Navier–Stokes equations. Comput Methods Appl Mech and Eng 32:199–259

    Article  MATH  MathSciNet  Google Scholar 

  6. Donea J, Fasoli-Stella P, Giuliani S (1977) Lagrangian and Eulerian finite element techniques for transient fluid-structure interaction problems. In: Transactions of the 4th international conference on structural mechanics in reactor technology, Paper B1/2

  7. Donea J, Giuliani S, Halleux JP (1982) An Arbitrary Lagrangian–Eulerian finite element method for transient dynamic fluid- interactions. Comput Methods Appl Mech Eng 33:689–723

    Article  MATH  Google Scholar 

  8. Zheng D, Ethier CR (2000) Accuracy and stability tests on a time-stepping finite element algorithm with the Arbitrary Lagrangian–Eulerian formulation. Comptes Rendus/Proceedings of the 8th conference of the CFD Society of Canada, vol. 1, 63–70

  9. Farhat C, Geuzaine P, Grandmont C (2001) The discrete geometric conservation law and the nonlinear stability of ALE schemes for the solution of flow problems on moving grids. J Comput Phys 174:669–694

    Article  MATH  MathSciNet  Google Scholar 

  10. Formaggia L, Nobile F (1999) A stability analysis for the Arbitrary Lagrangian–Eulerian formulation with finite elements. East West J Numer Math 7:105–131

    MATH  MathSciNet  Google Scholar 

  11. Franca LP, Frey SL, Hughes TJR (1992) Stabilized finite element methods: I. Application to the advective-diffusive model. Comput Methods Appl Mech Eng 95(2):253–276

    Article  MATH  MathSciNet  Google Scholar 

  12. Franca LP, Hauke G, Masud A (2006) Revisiting stabilized element methods for the advective-diffusive equation. Comput Methods Appl Mech Eng 195:1560–1572

    Article  MATH  MathSciNet  Google Scholar 

  13. Guillard H, Farhat C (2000) On the significance of the geometric conservation laws for flow computations on moving meshes. Comput Methods Appl Mech Eng 190:1467–1482

    Article  MATH  MathSciNet  Google Scholar 

  14. Harari I (2004) Stability of semidiscrete formulations for parabolic problems at small time steps. Comput Methods Appl Mech Eng 193(1):1491–1516

    Article  MATH  MathSciNet  Google Scholar 

  15. Harari I, Hughes TJR (1992) What are C and h?: inequalities for the analysis and design of finite element methods. Comput Methods Appl Mech Eng 97:157–192

    Article  MATH  MathSciNet  Google Scholar 

  16. Hughes TJR (1995) Multiscale phenomena: Green’s functions, the Dirichlet-to-Neumann formulation, subgrid scale models, bubbles and the origins of stabilized methods. Comput Methods Appl Mech Eng 127:387–401

    Article  MATH  Google Scholar 

  17. Hughes TJR, Franca LP, Hulbert GM (1989) A new finite element formulation for computational fluid dynamics: VIII. The Galerkin/least-squares method for advective-diffusive equations. Comput Methods Appl Mech Eng 73:173–189

    Article  MATH  MathSciNet  Google Scholar 

  18. Hughes TJR, Liu WK, Zimmerman TK (1984) Lagrangian– finite element formulation for incompressible viscous flows. Comput Methods Appl Mech Eng 29:329–349

    Article  Google Scholar 

  19. Johnson AA, Tezduyar TE (1994) Mesh update strategies in parallel finite element computations of flow problems with moving boundaries and interfaces. Comput Methods Appl Mech Eng 119:73–94

    Article  MATH  Google Scholar 

  20. Khurram R, Masud A (2006) Multiscale/stabilized incompressible Navier–stokes equations for fluid-structure interaction. Comput Mech (in press)

  21. Lesoinne M, Farhat C (1993) Stability analysis of dynamic meshes for transient aeroelastic computations. AIAA Paper 93-3325, 11th AIAA computational fluid dynamics conference, Orlando, Florida, July 6–9

  22. Lesoinne M, Farhat C (1995) Geometric conservation laws for aeroelastic computations using unstructured dynamic meshes. AIAA Paper 95-1709-CP,1995

  23. Lesoinne M, Farhat C (1996) Geometric conservation laws for flow problems and moving boundaries and deformable meshes and their impact on aeroelastic computations. Comput Methods Appl Mech Eng 134:71–90

    Article  MATH  Google Scholar 

  24. Masud A (1993) A space-time finite element method for fluid-structure interaction. Ph.D. Thesis, Stanford University, April 1993

  25. Masud A (2004) Preface to the special issue on Stabilized and Multiscale Finite Element Methods. Comput Methods Appl Mechd Eng 193:iii–iv

    Article  MathSciNet  Google Scholar 

  26. Masud A, Bhanabhagwanwala M, Khurram R (2006) An adaptive mesh rezoning scheme for moving boundary flows and fluid-structure interaction. Comput Fluids (in press)

  27. Masud A, Hughes TJR(1997) A space-time Galerkin/Least squares finite element formulation of the Navier–Stokes equations for moving domain problems. Comput Methods Appl Mech Eng 146:91–126

    Article  MATH  MathSciNet  Google Scholar 

  28. Masud A, Khurram R (2004) A multiscale/stabilized finite element method for the advection-diffusion equation. Comput Methods Appl Mech Eng 193:1997–2018

    Article  MATH  Google Scholar 

  29. Rifai SM, Johan Z, Wang WP, Grisval JP, Hughes TJR, Ferencz RM (1999) Multiphysics simulation of flow-induced vibrations and aeroelasticity on parallel computing platforms. Comput Methods Appl Mech Eng 174:393–417

    Article  MATH  MathSciNet  Google Scholar 

  30. Stein K, Tezduyar TE, Benny R (2003) Mesh moving techniques for fluid-structure interactions with large displacements. J Appl Mech 70:58–63

    Article  MATH  Google Scholar 

  31. Stein K, Tezduyar TE, Benny R (2004) Automatic mesh update with the solid-extension mesh moving technique. Comput Methods Appl Mech Eng 193:2019–2032

    Article  MATH  Google Scholar 

  32. Stewart JR, Hughes TJR (1998) A tutorial in elementary finite element error analysis: A systematic presentation of a priori and a posteriori error estimates. Comput Methods Appl Mech Eng 158:1–22

    Article  MATH  MathSciNet  Google Scholar 

  33. Tezduyar TE (2003) Computation of moving boundaries and interfaces and stabilization parameters. Int J Numer Methods Fluids 43:555–575

    Article  MATH  MathSciNet  Google Scholar 

  34. Tezduyar TE, Behr M, Liou J (1992) A new strategy for finite element computations involving moving boundaries and interfaces. The deforming-spatial-domain/space-time procedure: I. The concept and the preliminary numerical tests. Comput Methods Appl Mech Eng 94:339–351

    MATH  MathSciNet  Google Scholar 

  35. Tezduyar TE, Behr M, Mittal S, Liou J (1992) A new strategy for finite element computations involving moving boundaries and interfaces. The deforming-spatial- domain/space-time procedure: II Computation of free-surface flows, two-liquid flows, and flows with drifting cylinders. Comput Methods Appl Mech Eng 94:353–371

    Article  MATH  MathSciNet  Google Scholar 

  36. Tezduyar TE, Osawa Y (2000) Finite element stabilization parameters computed from element matrices and vectors. Comput Methods Appl Mech Eng 190:411–430

    Article  MATH  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Civil & Materials Engineering, The University of Illinois at Chicago, Chicago, IL, 60607-7023, USA

    Arif Masud

Authors
  1. Arif Masud
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Arif Masud.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Masud, A. Effects of Mesh Motion on the Stability and Convergence of ALE Based Formulations for Moving Boundary Flows. Comput Mech 38, 430–439 (2006). https://doi.org/10.1007/s00466-006-0062-9

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00466-006-0062-9

Keywords

Search

Navigation