The $h^*$-Polynomials of Locally Anti-Blocking Lattice Polytopes and Their $\gamma$-Positivity

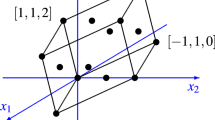
Abstract

A lattice polytope $\mathscr {P} \subset \mathbb {R}^d$ is called a locally anti-blocking polytope if for any closed orthant ${\mathbb R}^d_{\varepsilon }$ in $\mathbb {R}^d$, $\mathscr {P} \cap \mathbb {R}^d_{\varepsilon }$ is unimodularly equivalent to an anti-blocking polytope by reflections of coordinate hyperplanes. We give a formula for the $h^*$-polynomials of locally anti-blocking lattice polytopes. In particular, we discuss the $\gamma$-positivity of $h^*$-polynomials of locally anti-blocking reflexive polytopes.

1 Introduction

A lattice polytope is a convex polytope all of whose vertices have integer coordinates. A lattice polytope ${\mathscr {P}}\subset {\mathbb R}_{\ge 0}^d$ of dimension d is called anti-blocking if for any ${\mathbf{y}}=(y_1,\dots ,y_d) \in {\mathscr {P}}$ and ${\mathbf{x}}=(x_1,\dots ,x_d) \in {\mathbb R}^d$ with $0 \le x_i \le y_i$ for all i, it holds that ${\mathbf{x}}\in {\mathscr {P}}$. Anti-blocking polytopes were introduced and studied by Fulkerson [11, 12] in the context of combinatorial optimization. See, e.g., [35]. For $\varepsilon \in \{-1,1\}^d$ and ${\mathbf{x}}\in {\mathbb R}^d$, set $\varepsilon {\mathbf{x}}:=(\varepsilon _1 x_1,\ldots ,\varepsilon _d x_d) \in {\mathbb R}^d$. Given an anti-blocking lattice polytope ${\mathscr {P}}\subset {\mathbb R}_{\ge 0}^d$ of dimension d, we define

$$\begin{aligned} {\mathscr {P}}^{\pm }:=\{\varepsilon {\mathbf{x}}\in {\mathbb R}^d : \varepsilon \in \{-1,1\}^{d}, \, {\mathbf{x}}\in {\mathscr {P}}\}. \end{aligned}$$

Since ${\mathscr {P}}$ is an anti-blocking lattice polytope, ${\mathscr {P}}^\pm$ is convex (and a lattice polytope). Moreover, for any $\varepsilon \in \{-1,1\}^d$ and ${\mathbf{x}}\in {\mathscr {P}}^{\pm }$, we have $\varepsilon {\mathbf{x}}\in {\mathscr {P}}^{\pm }$. The polytope ${\mathscr {P}}^{\pm }$ is called an unconditional lattice polytope [23]. In general, ${\mathscr {P}}^{\pm }$ is symmetric with respect to all coordinate hyperplanes. In particular, the origin $\mathbf{0}$ of ${\mathbb R}^d$ is in the interior ${\text {int}}{\mathscr {P}}^{\pm }$. Given $\varepsilon =(\varepsilon _1,\ldots , \varepsilon _d) \in \{-1,1\}^d$, let ${\mathbb R}^d_{\varepsilon }$ denote the closed orthant $\{ (x_1,\ldots , x_d) \in {\mathbb R}^d : x_i \varepsilon _i \ge 0\ \hbox { for all}\ 1 \le i \le d\}$. A lattice polytope ${\mathscr {P}}\subset {\mathbb R}^d$ of dimension d is called locally anti-blocking [23] if, for each $\varepsilon \in \{-1,1\}^d$, there exists an anti-blocking lattice polytope ${\mathscr {P}}_{\varepsilon } \subset {\mathbb R}_{\ge 0}^d$ of dimension d such that ${\mathscr {P}}\cap {\mathbb R}^d_{\varepsilon }={\mathscr {P}}_{\varepsilon }^{\pm } \cap {\mathbb R}^d_{\varepsilon }$. Unconditional polytopes are locally anti-blocking.

In the present paper, we investigate the $h^*$-polynomials of locally anti-blocking lattice polytopes. First, we give a formula for the $h^*$-polynomials of locally anti-blocking lattice polytopes in terms of that of unconditional lattice polytopes.

Theorem 1.1

Let ${\mathscr {P}}\subset {\mathbb R}^d$ be a locally anti-blocking lattice polytope of dimension d and for each $\varepsilon \in \{-1,1\}^d$, let ${\mathscr {P}}_{\varepsilon }$ be an anti-blocking lattice polytope of dimension d such that ${\mathscr {P}}\cap {\mathbb R}^d_\varepsilon = {\mathscr {P}}_{\varepsilon }^\pm \cap {\mathbb R}^d_\varepsilon$. Then the $h^*$-polynomial of ${\mathscr {P}}$ satisfies

$$\begin{aligned} h^*({\mathscr {P}}, x)=\frac{1}{2^{d}}\sum _{\varepsilon \in \{-1,1\}^d}\!h^*({\mathscr {P}}_{\varepsilon }^\pm , x). \end{aligned}$$

In particular, $h^*({\mathscr {P}},x)$ is $\gamma$-positive if $h^*({\mathscr {P}}_{\varepsilon }^{\pm },x)$ is $\gamma$-positive for all $\varepsilon \in \{-1,1\}^d$.

Second, we discuss the $\gamma$-positivity of the $h^*$-polynomials of locally anti-blocking reflexive polytopes. A lattice polytope is called reflexive if the dual polytope is also a lattice polytope. Many authors have studied reflexive polytopes from viewpoints of combinatorics, commutative algebra, and algebraic geometry. In [15], Hibi characterized reflexive polytopes in terms of their $h^*$-polynomials. To be more precise, a lattice polytope of dimension d is (unimodularly equivalent to) a reflexive polytope if and only if the $h^*$-polynomial is a palindromic polynomial of degree d. On the other hand, in [23], locally anti-blocking reflexive polytopes were characterized. In fact, a locally anti-blocking lattice polytope ${\mathscr {P}}\subset {\mathbb R}^d$ of dimension d is reflexive if and only if for each $\varepsilon \in \{-1,1\}^d$, there exists a perfect graph $G_{\varepsilon }$ on $[d]:=\{1,\ldots ,d\}$ such that ${\mathscr {P}}\cap {\mathbb R}^d_{\varepsilon }={\mathscr {Q}}_{G_{\varepsilon }}^{\pm } \cap {\mathbb R}^d_{\varepsilon }$, where ${\mathscr {Q}}_{G_{\varepsilon }}$ is the stable set polytope of $G_{\varepsilon }$. Moreover, every locally anti-blocking reflexive polytope possesses a regular unimodular triangulation. This fact and the result of Bruns–Römer [5] imply that its $h^*$-polynomial is unimodal.

In the present paper, we discuss whether the $h^*$-polynomial of a locally anti-blocking reflexive polytope has a stronger property, which is called $\gamma$-positivity. In [31], a class of lattice polytopes ${\mathscr {B}}_G$ arising from finite simple graphs G on [d], which are called symmetric edge polytopes of type B, was introduced. Symmetric edge polytopes of type B are unconditional, and they are reflexive if and only if the underlying graphs are bipartite. Moreover, when they are reflexive, the $h^*$-polynomials are always $\gamma$-positive. On the other hand, in [30], another family of lattice polytopes ${\mathscr {C}}^{(e)}_P$ arising from finite partially ordered sets P on [d], which are called enriched chain polytopes, was given. Enriched chain polytopes are unconditional and reflexive, and their $h^*$-polynomials are always $\gamma$-positive. Combining these facts and Theorem 1.1, we know that, for a locally anti-blocking reflexive polytope ${\mathscr {P}}$, if every ${\mathscr {P}}\cap {\mathbb R}_\varepsilon ^d$ is the intersection of ${\mathbb R}^d_{\varepsilon }$ and either an enriched chain polytope or a symmetric edge reflexive polytope of type B, then the $h^*$-polynomial of ${\mathscr {P}}$ is $\gamma$-positive (Corollary 4.2). By using this result, we show that the $h^*$-polynomials of several classes of reflexive polytopes are $\gamma$-positive.

In Sect. 5, we will discuss $\gamma$-positivity of the $h^*$-polynomials of symmetric edge polytopes of type A, which are reflexive polytopes arising from finite simple graphs. In [21], it was shown that the $h^*$-polynomials of the symmetric edge polytopes of type A of complete bipartite graphs are $\gamma$-positive. We will show that for a large class of finite simple graphs, which includes complete bipartite graphs, the $h^*$-polynomials of the symmetric edge polytopes of type A are $\gamma$-positive (Sect. 5.1). Moreover, by giving explicit $h^*$-polynomials of del Pezzo polytopes and pseudo-del Pezzo polytopes, we will show that the $h^*$-polynomial of every pseudo-symmetric simplicial reflexive polytope is $\gamma$-positive (Theorem 5.8).

In Sect. 6, we will discuss $\gamma$-positivity of $h^*$-polynomials of twinned chain polytopes ${\mathscr {C}}_{P,Q} \subset {\mathbb R}^d$, which are reflexive polytopes arising from two finite partially ordered sets P and Q on [d]. In [39], it was shown that twinned chain polytopes ${\mathscr {C}}_{P,Q}$ are locally anti-blocking and each ${\mathscr {C}}_{P,Q} \cap {\mathbb R}_{\varepsilon }^d$ is the intersection of ${\mathbb R}^d_{\varepsilon }$ and an enriched chain polytope. Hence the $h^*$-polynomials of ${\mathscr {C}}_{P,Q}$ are $\gamma$-positive. We will give a formula for the $h^*$-polynomials of twinned chain polytopes in terms of the left peak polynomials of finite partially ordered sets (Theorem 6.3). Moreover, we will define enriched (P, Q)-partitions of P and Q, and show that the Ehrhart polynomial of the twined chain polytope ${\mathscr {C}}_{P,Q}$ of P and Q coincides with a counting polynomial of enriched (P, Q)-partitions (Theorem 6.8).

This paper is organized as follows: In Sect. 2, we will review the theory of Ehrhart polynomials, $h^*$-polynomials, and reflexive polytopes. In Sect. 3, we will introduce several classes of anti-blocking polytopes and unconditional polytopes. In Sect. 4, we will investigate the $h^*$-polynomials of locally anti-blocking lattice polytopes. In particular, we will prove Theorem 1.1. We will discuss symmetric edge polytopes of type A in Sect. 5, and twinned chain polytopes in Sect. 6.

2 Ehrhart Theory and Reflexive Polytopes

In this section, we review the theory of Ehrhart polynomials, $h^*$-polynomials, and reflexive polytopes. Let ${\mathscr {P}}\subset {\mathbb R}^d$ be a lattice polytope of dimension d. Given a positive integer m, we define

$$\begin{aligned} L_{{\mathscr {P}}}(m)=|m {\mathscr {P}}\cap {\mathbb Z}^d|. \end{aligned}$$

Ehrhart [10] proved that $L_{{\mathscr {P}}}(m)$ is a polynomial in m of degree d with the constant term 1. We say that $L_{{\mathscr {P}}}(m)$ is the Ehrhart polynomial of ${\mathscr {P}}$. The generating function of the lattice point enumerator, i.e., the formal power series

$$\begin{aligned} \text {Ehr}_{\mathscr {P}}(x)=1+\sum \limits _{k=1}^{\infty }L_{{\mathscr {P}}}(k)x^k \end{aligned}$$

is called the Ehrhart series of ${\mathscr {P}}$. It is well known that it can be expressed as a rational function of the form

$$\begin{aligned} \text {Ehr}_{\mathscr {P}}(x)=\frac{h^*({\mathscr {P}},x)}{(1-x)^{d+1}}. \end{aligned}$$

Then $h^*({\mathscr {P}},x)$ is a polynomial in x of degree at most d with nonnegative integer coefficients [36] and it is called the $h^*$-polynomial (or the $\delta$-polynomial) of ${\mathscr {P}}$. Moreover, one has ${\text {Vol}}({\mathscr {P}})=h^*({\mathscr {P}},1)$, where ${\text {Vol}}({\mathscr {P}})$ is the normalized volume of ${\mathscr {P}}$.

A lattice polytope ${\mathscr {P}}\subset {\mathbb R}^d$ of dimension d is called reflexive if the origin of ${\mathbb R}^d$ is a unique lattice point belonging to the interior of ${\mathscr {P}}$ and its dual polytope

$$\begin{aligned}{\mathscr {P}}^\vee :=\{{\mathbf{y}}\in {\mathbb R}^d : \langle {\mathbf{x}},{\mathbf{y}}\rangle \le 1 \ \text {for all}\ {\mathbf{x}}\in {\mathscr {P}}\}\end{aligned}$$

is also a lattice polytope, where $\langle {\mathbf{x}},{\mathbf{y}}\rangle$ is the usual inner product of ${\mathbb R}^d$. It is known that reflexive polytopes correspond to Gorenstein toric Fano varieties, and they are related to mirror symmetry (see, e.g., [3, 7]). In each dimension there exist only finitely many reflexive polytopes up to unimodular equivalence [25] and all of them are known up to dimension 4 [24]. In [15], Hibi characterized reflexive polytopes in terms of their $h^*$-polynomials. We recall that a polynomial $f \in {\mathbb R}[x]$ of degree d is said to be palindromic if $f(x)=x^df(x^{-1})$. Note that if a lattice polytope of dimension d has interior lattice points, then the degree of its $h^*$-polynomial is equal to d.

Proposition 2.1

[15]Let ${\mathscr {P}}\subset {\mathbb R}^d$ be a lattice polytope of dimension d with $\mathbf{0} \in {\text {int}}{\mathscr {P}}$. Then ${\mathscr {P}}$ is reflexive if and only if $h^*({\mathscr {P}},x)$ is a palindromic polynomial of degree d.

Next, we review some properties of polynomials. Let $f= \sum _{i=0}^{d}a_i x^i$ be a polynomial with real coefficients and $a_d \ne 0$. We now focus on the following properties.

• (RR) We say that f is real-rooted if all its roots are real.

• (LC) We say that f is log-concave if $a_i^2 \ge a_{i-1}a_{i+1}$ for all i.

• (UN) We say that f is unimodal if $a_0 \le a_1 \le \cdots \le a_k \ge \cdots \ge a_d$ for some k.

If all its coefficients are nonnegative, then these properties satisfy the implications

$$\begin{aligned} \mathrm{(RR)}\ \Rightarrow \ \mathrm{(LC)}\ \Rightarrow \ \mathrm{(UN)}. \end{aligned}$$

On the other hand, the polynomial f is $\gamma$-positive if f is palindromic and there are $\gamma _0,\gamma _1,\ldots ,\gamma _{\lfloor d/2\rfloor } \ge 0$ such that $f(x)=\sum _{i \ge 0}\gamma _ix^i (1+x)^{d-2i}$. The polynomial $\sum _{i \ge 0}\gamma _ix^i$ is called the $\gamma$-polynomial of f. We can see that a $\gamma$-positive polynomial is real-rooted if and only if its $\gamma$-polynomial is real-rooted. If f is palindromic and real-rooted, then it is $\gamma$-positive. Moreover, if f is $\gamma$-positive, then it is unimodal. See, e.g., [2, 34] for details.

For a given lattice polytope, a fundamental problem within the field of Ehrhart theory is to determine if its $h^*$-polynomial is unimodal. One famous instance is given by reflexive polytopes that possess a regular unimodular triangulation.

Proposition 2.2

[5]Let ${\mathscr {P}}\subset {\mathbb R}^d$ be a reflexive polytope of dimension d. If P possesses a regular unimodular triangulation, then $h^*({\mathscr {P}}, x)$ is unimodal.

It is known that if a reflexive polytope possesses a flag regular unimodular triangulation all of whose maximal simplices contain the origin, then the $h^*$-polynomial coincides with the h-polynomial of a flag triangulation of a sphere [5]. For the h-polynomial of a flag triangulation of a sphere, Gal [13] conjectured the following:

Conjecture 2.3

The h-polynomial of any flag triangulation of a sphere is $\gamma$-positive.

3 Classes of Anti-Blocking Polytopes and Unconditional Polytopes

In this section, we introduce several classes of anti-blocking polytopes and unconditional polytopes. Throughout this section, we associate each subset $F \subset [d]$ with a (0, 1)-vector ${\mathbf{e}}_F \!=\! \sum _{i \in F} {\mathbf{e}}_i \!\in \! {\mathbb R}^d$, where each ${\mathbf{e}}_i$ is the ith unit coordinate vector in ${\mathbb R}^d$.

3.1 (0, 1)-Polytopes Arising from Simplicial Complexes

Let $\Delta$ be a simplicial complex on the vertex set [d]. Then $\Delta$ is a collection of subsets of [d] with $\{i\} \in \Delta$ for all $i \in [d]$ such that if $F \in \Delta$ and $F' \subset F$, then $F' \in \Delta$. In particular $\emptyset \in \Delta$ and ${\mathbf{e}}_{\emptyset }= \mathbf{0}$. Let ${\mathscr {P}}_\Delta$ denote the convex hull of $\{ {\mathbf{e}}_F \in {\mathbb R}^d : F \in \Delta \}$. The following is an important observation.

Proposition 3.1

Let ${\mathscr {P}}\subset {\mathbb R}_{\ge 0}^d$ be a (0, 1)-polytope of dimension d. Then ${\mathscr {P}}$ is anti-blocking if and only if there exists a simplicial complex $\Delta$ on [d] such that ${\mathscr {P}}= {\mathscr {P}}_\Delta$.

3.2 Stable Set Polytopes

Let G be a finite simple graph on the vertex set [d] and E(G) the set of edges of G. (A finite graph G is called simple if G possesses no loop and no multiple edge.) A subset $W \subset [d]$ is called stable if, for all i and j belonging to W with $i \ne j$, one has $\{i,j\} \notin E(G)$. We remark that a stable set is often called an independent set. Let S(G) denote the set of all stable sets of G. One has $\emptyset \in S(G)$ and $\{ i \} \in S(G)$ for each $i \in [d]$. The stable set polytope ${\mathscr {Q}}_G \subset {\mathbb R}^{d}$ of G is the (0, 1)-polytope defined by

$$\begin{aligned} {\mathscr {Q}}_G:={\text {conv}}{\{{\mathbf{e}}_W \in {\mathbb R}^d : W \in S(G) \}}. \end{aligned}$$

Then one has $\dim {\mathscr {Q}}_G = d$. Since we can regard S(G) as a simplicial complex on [d], ${\mathscr {Q}}_G$ is an anti-blocking polytope.

Locally anti-blocking reflexive polytopes are characterized by stable set polytopes. A clique of G is a subset $W \subset [d]$ that is a stable set of the complement graph ${\overline{G}}$ of G. The chromatic number of G is the smallest integer $t \ge 1$ for which there exist stable sets $W_{1}, \ldots , W_{t}$ of G with $[d] = W_{1} \cup \cdots \cup W_{t}$. A finite simple graph G is said to be perfect if, for any induced subgraph H of G including G itself, the chromatic number of H is equal to the maximal cardinality of cliques of H. See, e.g., [9] for details on graph theoretical terminology.

Proposition 3.2

[23]Let ${\mathscr {P}}\subset {\mathbb R}^d$ be a locally anti-blocking lattice polytope of dimension d. Then ${\mathscr {P}}\subset {\mathbb R}^d$ is reflexive if and only if, for each $\varepsilon \in \{-1,1\}^d$, there exists a perfect graph $G_{\varepsilon }$ on [d] such that ${\mathscr {P}}\cap {\mathbb R}^d_{\varepsilon }={\mathscr {Q}}_{G_{\varepsilon }}^{\pm } \cap {\mathbb R}^d_{\varepsilon }$.

3.3 Chain Polytopes and Enriched Chain Polytopes

Let $(P, <_P)$ be a partially ordered set (poset, for short) on [d]. A subset A of [d] is called an antichain of P if all i and j belonging to A with $i \ne j$ are incomparable in P. In particular, the empty set $\emptyset$ and each 1-element subset $\{i\}$ are antichains of P. Let ${\mathscr {A}}(P)$ denote the set of antichains of P. In [37], Stanley introduced the chain polytope ${\mathscr {C}}_P$ of P defined by

$$\begin{aligned} {\mathscr {C}}_P:={\text {conv}}{\{ {\mathbf{e}}_A \in {\mathbb R}^d : A \in {\mathscr {A}}(P) \}}. \end{aligned}$$

It is known that chain polytopes are stable set polytopes. Indeed, let $G_P$ be the finite simple graph on [d] such that $\{i,j\} \in E(G_P)$ if and only if $i <_P j$ or $j <_P i$. We call $G_P$ the comparability graph of P. It then follows that ${\mathscr {A}}(P)=S(G_P)$. Hence the chain polytope ${\mathscr {C}}_P$ is the stable set polytope ${\mathscr {Q}}_{G_P}$. Therefore, chain polytopes are anti-blocking polytopes. We remark that any comparability graph is perfect.

On the other hand, the enriched chain polytope ${\mathscr {C}}^{(e)}_P$ of P is the unconditional lattice polytope defined by ${\mathscr {C}}^{(e)}_P:={\mathscr {C}}_P^{\pm }$. In [30], it was shown that the Ehrhart polynomial of ${\mathscr {C}}^{(e)}_P$ coincides with a counting polynomial of left enriched P-partitions. We assume that P is naturally labeled. A map $f:P \rightarrow {\mathbb Z}\setminus \{0\}$ is called an enriched P-partition [38] if, for all $x, y \in P$ with $x <_P y$, f satisfies

$$\begin{aligned} |f(x)| \le |f(y)|\quad \text {and}\quad |f(x)| = |f(y)|\ \Rightarrow \ f(y) > 0. \end{aligned}$$

A map $f:P \rightarrow {\mathbb Z}$ is called a left enriched P-partition [33] if, for all $x, y \in P$ with $x <_P y$, f satisfies

$$\begin{aligned} |f(x)| \le |f(y)|\quad \text {and}\quad |f(x)| = |f(y)|\ \Rightarrow \ f(y) \ge 0. \end{aligned}$$

The symbol $\Omega _P^{(\ell )}(m)$ will denote the number of left enriched P-partitions $f:P \rightarrow {\mathbb Z}$ with $|f(x)| \le m$ for any $x \in P$, which is called the left enriched order polynomial of P.

Proposition 3.3

[30]Let P be a naturally labeled finite poset on [d]. Then one has

$$\begin{aligned} L_{{\mathscr {C}}^{(e)}_P}(m) =\Omega _P^{(\ell )} (m). \end{aligned}$$

Given a linear extension $\pi = (\pi _1,\dots ,\pi _d)$ of a finite poset P on [d], a left peak of $\pi$ is an index $1 \le i \le d-1$ such that $\pi _{i-1} <\pi _i > \pi _{i+1}$, where we set $\pi _0 =0$. Let $\mathrm{pk}^{(\ell )}(\pi )$ denote the number of left peaks of $\pi$. Then the left peak polynomial $W_{P}^{(\ell )} (x)$ of P is defined by

$$\begin{aligned} W_{P}^{(\ell )} (x) \,=\!\sum _{\pi \in {{\mathscr {L}}} (P)}\!\! x^{\ \mathrm{pk}^{(\ell )}(\pi )}, \end{aligned}$$

where ${\mathscr {L}}(P)$ is the set of linear extensions of P.

Proposition 3.4

[30]Let P be a naturally labeled finite poset on [d]. Then the $h^*$-polynomial of ${\mathscr {C}}^{(e)}_P$ is

$$\begin{aligned} h^*({\mathscr {C}}^{(e)}_P\!, x)= (x+1)^d W_{P}^{(\ell )} \biggl ( \frac{4x}{(x+1)^2} \biggl ). \end{aligned}$$

In particular, $h^*({\mathscr {C}}^{(e)}_P, x)$ is $\gamma$-positive.

Note that if Q is a finite poset that is obtained from P by reordering the label, then ${\mathscr {C}}^{(e)}_P$ and ${\mathscr {C}}^{(e)}_Q$ are unimodularly equivalent. Hence the $h^*$-polynomials of enriched chain polytopes are always $\gamma$-positive.

3.4 Symmetric Edge Polytopes of Type B

Let G be a finite simple graph on [d]. We set

$$\begin{aligned} B_G :={\text {conv}}{\left( \{ \mathbf{0} , {\mathbf{e}}_1,\ldots ,{\mathbf{e}}_d\} \cup \{{\mathbf{e}}_i + {\mathbf{e}}_j : \{i,j\} \in E(G) \}\right) }. \end{aligned}$$

Then $B_G = {\mathscr {P}}_\Delta$ where $\Delta$ is a simplicial complex on [d] obtained by regarding G as a 1-dimensional simplicial complex. The symmetric edge polytope of type B of G is the unconditional lattice polytope defined by ${\mathscr {B}}_G:= B_G^{\pm }$.

Proposition 3.5

[31]Let G be a finite simple graph on [d]. Then ${\mathscr {B}}_G$ is reflexive if and only if G is bipartite.

A hypergraph is a pair ${\mathscr {H}}= (V, E)$, where $E=\{e_1,\ldots ,e_n\}$ is a finite multiset of non-empty subsets of $V=\{v_1,\ldots ,v_m\}$. Elements of V are called vertices and the elements of E are the hyperedges. Then we can associate ${\mathscr {H}}$ to a bipartite graph ${\text {Bip}}{\mathscr {H}}$ with a bipartition $V \cup E$, such that $\{v_i, e_j\}$ is an edge of ${\text {Bip}}{\mathscr {H}}$ if $v_i \in e_j$. Assume that ${\text {Bip}}{\mathscr {H}}$ is connected. A hypertree in ${\mathscr {H}}$ is a function $\mathbf{f}:E \rightarrow \{0,1,\ldots \}$ such that there exists a spanning tree $\Gamma$ of ${\text {Bip}}{\mathscr {H}}$ whose vertices have degree $\mathbf{f} (e) +1$ at each $e \in E$. Then we say that $\Gamma$ induces $\mathbf{f}$. Let $B_{\mathscr {H}}$ denote the set of all hypertrees in ${\mathscr {H}}$. A hyperedge $e_j \in E$ is said to be internally active with respect to the hypertree $\mathbf{f}$ if it is not possible to decrease $\mathbf{f}(e_j)$ by 1 and increase $\mathbf{f}(e_{j'})$, $j' < j$, by 1 so that another hypertree results. We call a hyperedge internally inactive with respect to a hypertree if it is not internally active and denote the number of such hyperedges of $\mathbf{f}$ by ${\overline{\iota }} (\mathbf{f})$. Then the interior polynomial of ${\mathscr {H}}$ is the generating function $I_{\mathscr {H}}(x)=\sum _{\mathbf{f} \in B_{\mathscr {H}}} x^{ {\overline{\iota }} (\mathbf{f})}$. It is known [22, Prop. 6.1] that ${\text {deg}}I_{\mathscr {H}}(x)\le \min {\{|V|,|E|\}}-1$. If $G={\text {Bip}}{\mathscr {H}}$, then we set $I_G(x)=I_{\mathscr {H}}(x)$.

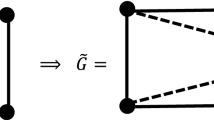
Assume that G is a bipartite graph with a bipartition $V_1 \cup V_2 =[d]$. Then let ${\widetilde{G}}$ be a connected bipartite graph on $[d+2]$ whose edge set is

$$\begin{aligned} E({\widetilde{G}}) = E(G) \cup \{ \{i, d+1\} : i \in V_1\} \cup \{ \{j, d+2\} : j \in V_2 \cup \{d+1\}\}. \end{aligned}$$

Proposition 3.6

[31]Let G be a bipartite graph on [d]. Then the $h^*$-polynomial of the reflexive polytope ${\mathscr {B}}_G$ is

$$\begin{aligned} h^*({\mathscr {B}}_G, x)= (x+1)^d I_{{\widetilde{G}}} \biggl (\frac{4x}{(x+1)^2} \biggr ). \end{aligned}$$

In particular, $h^*({\mathscr {B}}_G, x)$ is $\gamma$-positive.

4 $h^*$-Polynomials of Locally Anti-Blocking Lattice Polytopes

In the present section, we prove Theorem 1.1, that is, a formula for the $h^*$-polynomials of locally anti-blocking lattice polytopes in terms of that of unconditional lattice polytopes. Given a subset $J=\{j_1,\dots , j_r\}$ of [d], let

$$\begin{aligned} \pi _J :{\mathbb R}^d \rightarrow {\mathbb R}^r, \qquad \pi _J((x_1,\dots ,x_d)) = (x_{j_1},\dots ,x_{j_r}) \end{aligned}$$

denote the projection map. (Here $\pi _\emptyset$ is the zero map.)

Proposition 4.1

Let ${\mathscr {P}}\subset {\mathbb R}_{\ge 0}^d$ be an anti-blocking lattice polytope. Then we have

$$\begin{aligned} h^*({\mathscr {P}}^\pm , x)\,=\,\sum _{j=0}^d 2^j (x-1)^{d-j}\!\!\sum _{J \subset [d], \, |J| = j}\!\! h^*(\pi _J ({\mathscr {P}}), x). \end{aligned}$$

Proof

The proof is similar to the discussion in [31, proof of Prop. 3.1]. The intersection of ${\mathscr {P}}^\pm \cap {\mathbb R}_\varepsilon ^d$ and ${\mathscr {P}}^\pm \cap {\mathbb R}_{\varepsilon '}^d$ is of dimension $d-1$ if and only if $\varepsilon - \varepsilon ' \in \{\pm 2 {\mathbf{e}}_1, \ldots , \pm 2 {\mathbf{e}}_d\}$. Moreover, if $\varepsilon - \varepsilon ' = 2 {\mathbf{e}}_k$, then

$$\begin{aligned} ({\mathscr {P}}^\pm \cap {\mathbb R}_\varepsilon ^d) \cap ({\mathscr {P}}^\pm \cap {\mathbb R}_{\varepsilon '}^d)={\mathscr {P}}^\pm \cap {\mathbb R}_\varepsilon ^d \cap {\mathbb R}_{\varepsilon '}^d\simeq & {} \,\,\pi _{[d] \setminus \{k\}} ({\mathscr {P}}^\pm ) \cap {\mathbb R}_{ \pi _{[d] \setminus \{k\}} (\varepsilon )}^{d-1}\\\simeq & {} \,\pi _{[d] \setminus \{k\}} ({\mathscr {P}}). \end{aligned}$$

Hence the Ehrhart polynomial $L_{{\mathscr {P}}^\pm }(m)$ satisfies the following:

$$\begin{aligned} L_{{\mathscr {P}}^\pm }(m)\, =\, \sum _{j=0}^d2^j (-1)^{d-j}\!\!\sum _{J \subset [d], \, |J| = j}\!\! L_{\pi _J ({\mathscr {P}})}(m). \end{aligned}$$

Thus the Ehrhart series satisfies

$$\begin{aligned} \frac{h^*({\mathscr {P}}^\pm , x)}{(1-x)^{d+1}}\,=\,\sum _{j=0}^d2^j (-1)^{d-j}\!\!\sum _{J \subset [d], \, |J| = j}\!\frac{h^*(\pi _J ({\mathscr {P}}), x)}{(1-x)^{j+1}}, \end{aligned}$$

as desired. $\square$

We now prove Theorem 1.1.

Proof of Theorem 1.1

Given $J = \{j_1,\dots , j_r\} \subset [d]$ and $\varepsilon \in \{-1,1\}^{r}$, let

$$\begin{aligned} {\mathbb R}_{J, \varepsilon }^d \,=\,\{ {\mathbf{x}}= (x_1,\ldots , x_d) \in {\mathbb R}^d :\pi _J({\mathbf{x}}) \in {\mathbb R}_\varepsilon ^r\ \text {and}\ x_j =0\ \text {for all}\ j \notin J \}. \end{aligned}$$

It then follows that ${\mathscr {P}}\cap {\mathbb R}_{J, \varepsilon }^d$ is equal to $\pi _J({\mathscr {P}}_{\varepsilon '})^\pm \cap {\mathbb R}_\varepsilon ^r$, where $\pi _J(\varepsilon ') = \varepsilon$. Note that, given $J = \{j_1,\dots , j_r\} \subset [d]$ and $\varepsilon \in \{-1,1\}^{r}$, we have $| \{ \varepsilon ' \in \{-1,1\}^d : \pi _J(\varepsilon ') = \varepsilon \} |= 2^{d-r}$. Thus

$$\begin{aligned} h^*({\mathscr {P}}, x)&\,=\,\sum _{j=0}^d (x-1)^{d-j}\!\!\sum _{J \subset [d],\, |J| = j }\ \sum _{\varepsilon \in \{-1,1\}^j}\!\!h^*({\mathscr {P}}\cap {\mathbb R}_{J, \varepsilon }^d, x)\\&\,=\,\sum _{j=0}^d (x-1)^{d-j}\!\!\sum _{\varepsilon \in \{-1,1\}^d}\ \sum _{J \subset [d],\, |J| = j }\!\!\frac{h^*(\pi _J({\mathscr {P}}_{\varepsilon }), x)}{2^{d-j}}\\&\,=\,\frac{1}{2^{d}}\sum _{\varepsilon \in \{-1,1\}^d}\ \sum _{j=0}^d 2^j (x-1)^{d-j}\!\!\sum _{J \subset [d],\, |J| = j }\!\!h^*(\pi _J({\mathscr {P}}_{\varepsilon }), x)\\&=\frac{1}{2^{d}}\sum _{\varepsilon \in \{-1,1\}^d}\!\!h^*({\mathscr {P}}_\varepsilon ^\pm , x) \end{aligned}$$

by Proposition 4.1. $\square$

Combining Theorem 1.1 with Propositions 3.4 and 3.6, we have

Corollary 4.2

Let ${\mathscr {P}}\subset {\mathbb R}^d$ be a locally anti-blocking reflexive polytope. If every ${\mathscr {P}}\cap {\mathbb R}_\varepsilon ^d$ is the intersection of ${\mathbb R}_\varepsilon ^d$ and either an enriched chain polytope or a symmetric edge reflexive polytope of type B, then the $h^*$-polynomial of ${\mathscr {P}}$ is $\gamma$-positive.

Finally, we conjecture the following.

Conjecture 4.3

The $h^*$-polynomial of any locally anti-blocking reflexive polytope is $\gamma$-positive.

Thanks to Theorem 1.1 and Proposition 3.2, in order to prove Conjecture 4.3, it is enough to study unconditional lattice polytopes ${\mathscr {Q}}_G^\pm$ where ${\mathscr {Q}}_G$ is the stable set polytope of a perfect graph G.

5 Symmetric Edge Polytopes of Type A

Let G be a finite simple graph on the vertex set [d] and the edge set E(G). The symmetric edge polytope ${{\mathscr {A}}}_G \subset {\mathbb R}^d$ of type A is the convex hull of the set

$$\begin{aligned} A(G) = \{ \pm ( {\mathbf{e}}_i - {\mathbf{e}}_j ) \in {\mathbb R}^d: \{ i, j\} \in E(G) \}. \end{aligned}$$

The polytope ${{\mathscr {A}}}_G$ is introduced in [26, 28] and called a “symmetric edge polytope of G.”

Example 5.1

Let G be a tree on [d]. Then ${\mathscr {A}}_G$ is unimodularly equivalent to a $(d-1)$-dimensional cross polytope. Hence we have $h^*({\mathscr {A}}_G,x)= (x+1)^{d-1}$.

It is known [26, Prop. 4.1] that the dimension of ${\mathscr {A}}_G$ is $d-1$ if and only if G is connected. Higashitani [20] proved that ${{\mathscr {A}}}_G$ is simple if and only if ${{\mathscr {A}}}_G$ is smooth Fano if and only if G contains no even cycles. It is known [26, 28] that ${{\mathscr {A}}}_G$ is unimodularly equivalent to a reflexive polytope having a regular unimodular triangulation. In particular, the $h^*$-polynomial of ${{\mathscr {A}}}_{G}$ is palindromic and unimodal. For a complete bipartite graph $K_{\ell , m}$, it is known [21] that the $h^*$-polynomial of ${{\mathscr {A}}}_{K_{\ell , m}}$ is real-rooted and hence $\gamma$-positive.

5.1 Recursive Formulas for $h^*$-Polynomials

In this section, we give several recursive formulas of $h^*$-polynomials of ${\mathscr {A}}_G$ when G belongs to certain classes of graphs. By the following fact, we may assume that G is 2-connected if needed.

Proposition 5.2

Let G be a graph and let $G_1,\ldots , G_s$ be 2-connected components of G. Then the $h^*$-polynomial of ${{\mathscr {A}}}_{G}$ satisfies

$$\begin{aligned} h^*({\mathscr {A}}_G,x)=h^*({\mathscr {A}}_{G_1},x) \cdots h^*({\mathscr {A}}_{G_s},x). \end{aligned}$$

Proof

Since ${\mathscr {A}}_G$ is the free sum of reflexive polytopes ${\mathscr {A}}_{G_1}, \ldots , {\mathscr {A}}_{G_s}$, a desired conclusion follows from [4, Thm. 1]. $\square$

The suspension ${\widehat{G}}$ of a graph G is the graph on the vertex set $[d+1]$ and the edge set

$$\begin{aligned} E(G)\cup \{\{i, d+1\} : i \in [d]\}. \end{aligned}$$

We now study the $h^*$-polynomial of ${{\mathscr {A}}}_{{\widehat{G}}}$. Given a subset $S \subset [d]$,

$$\begin{aligned} E_S := \{ e \in E(G) : |e \cap S| =1 \} \end{aligned}$$

is called a cut of G. For example, we have $E_\emptyset = E_{[d]} = \emptyset$. In general, it follows that $E_S = E_{[d] \setminus S}$. We identify $E_S$ with the subgraph of G on the vertex set [d] and the edge set $E_S$. By definition, $E_S$ is a bipartite graph. Let ${\text {Cut}}(G)$ be the set of all cuts of G. Note that $|{{\text {Cut}}(G)}| = 2^{d-1}$. From Theorem 1.1 and Proposition 3.6, we have the following.

Theorem 5.3

Let G be a finite graph on [d]. Then ${{\mathscr {A}}}_{{\widehat{G}}}$ is unimodularly equivalent to a locally anti-blocking reflexive polytope whose $h^*$-polynomial is

$$\begin{aligned} h^*({{\mathscr {A}}}_{{\widehat{G}}}, x)=\frac{1}{2^{d-1}}\sum _{H \in {\text {Cut}}(G)}\!\!h^*({{\mathscr {B}}}_H, x)=(x+1)^d f_G \bigg ( \frac{4x}{(x+1)^2} \bigg ), \end{aligned}$$

where

$$\begin{aligned} f_G (x)= \frac{1}{2^{d-1}} \sum _{H \in {\text {Cut}}(G)} \!\!I_{{\widetilde{H}}} (x). \end{aligned}$$

In particular, $h^*({{\mathscr {A}}}_{{\widehat{G}}}, x)$ is $\gamma$-positive. Moreover, $h^*({{\mathscr {A}}}_{{\widehat{G}}}, x)$ is real-rooted if and only if $f_G(x)$ is real-rooted.

Proof

Let ${{\mathscr {P}}} \subset {\mathbb R}^d$ be the convex hull of

$$\begin{aligned} \{ \pm {\mathbf{e}}_1, \dots , \pm {\mathbf{e}}_d\}\cup \{ \pm ( {\mathbf{e}}_i - {\mathbf{e}}_j ): \{ i, j\} \in E(G) \}. \end{aligned}$$

Then ${{\mathscr {A}}}_{{\widehat{G}}}$ is lattice isomorphic to ${\mathscr {P}}$. Given $\varepsilon = (\varepsilon _1,\ldots , \varepsilon _d) \in \{-1,1\}^d$, let $S_\varepsilon = \{ i \in [d] : \varepsilon _i = 1\}$. Then ${{\mathscr {P}}} \cap {\mathbb R}_\varepsilon ^d$ is the convex hull of

$$\begin{aligned} \{\mathbf{0}\} \cup \{ \varepsilon _i {\mathbf{e}}_i : i \in [d] \}\cup \{ {\mathbf{e}}_i - {\mathbf{e}}_j : \{ i, j\} \in E_{S_\varepsilon } ,\, i \in S_\varepsilon \}. \end{aligned}$$

Hence ${{\mathscr {P}}} \cap {\mathbb R}_\varepsilon ^d = {\mathscr {B}}_{E_{S_\varepsilon }} \cap {\mathbb R}_\varepsilon ^d$. Thus ${\mathscr {P}}$ is a locally anti-blocking polytope and

$$\begin{aligned} h^*({{\mathscr {A}}}_{{\widehat{G}}}, x)=\frac{1}{2^{d-1}}\sum _{H \in {\text {Cut}}(G)}\!\!h^*({{\mathscr {B}}}_H, x) \end{aligned}$$

by Theorem 1.1. $\square$

Let G be a graph and let $e=\{i,j\}$ be an edge of G. Then the graph G/e obtained by the procedure

• (i) Delete e and identify the vertices i and j

• (ii) Delete the multiple edges that may be created while (i)

is called the graph obtained from G by contracting the edge e. Next, we will show that, for any bipartite graph G and $e \in E(G)$, $h^*({{\mathscr {A}}}_G, x)$ is $\gamma$-positive if and only if so is $h^*({\mathscr {A}}_{G/e}, x)$. In order to show this fact, we need the theory of Gröbner bases of toric ideals. Given a graph G on the vertex set [d] and the edge set $E(G)=\{e_1 ,\dots , e_n\}$, let

$$\begin{aligned} {\mathscr {R}}=K[t_1, t_1^{-1}\!, \dots , t_d, t_d^{-1}\!,s ] \end{aligned}$$

be the Laurent polynomial ring over a field K and let

$$\begin{aligned} {\mathscr {S}}=K[x_1, \dots , x_n, y_1, \dots , y_n, z] \end{aligned}$$

be the polynomial ring over K. We define the ring homomorphism $\pi :{\mathscr {S}}\rightarrow {\mathscr {R}}$ by setting $\pi (z) = s$, $\pi (x_k) = t_i t_j^{-1} s$ and $\pi (y_k) = t_i^{-1} t_j s$ if $e_k = \{i,j\} \in E(G)$ and $i<j$. The toric ideal $I_{{\mathscr {A}}_G}$ of ${\mathscr {A}}_G$ is the kernel of $\pi$. (See, e.g., [14] for details on toric ideals and Gröbner bases.) We now recall the notation given in [21]. For any oriented edge $e_i$, let $p_i$ denote the corresponding variable, i.e., $p_i = x_i$ or $p_i = y_i$ depending on the orientation, and let $\{p_i, q_i\} = \{x_i, y_i\}$. Let ${\mathscr {G}}(G)$ be the set of all binomials f satisfying one of the following:

$$\begin{aligned} f\,=\, \prod _{e_i \in I} p_i \,-\! \prod _{e_i \in C \setminus I} q_i, \end{aligned}$$

(1)

where C is an even cycle in G of length 2k with a fixed orientation, and I is a k-subset of C such that $e_\ell \notin I$ for $\ell =\min {\{i:e_i\in C\}}$;

$$\begin{aligned} f\,=\, \prod _{e_i \in I} p_i - z\prod _{e_i \in C \setminus I} q_i, \end{aligned}$$

(2)

where C is an odd cycle in G of length $2k+1$ and I is a $(k+1)$-subset of C;

$$\begin{aligned} f = x_i y_i - z^2, \end{aligned}$$

(3)

where $1 \le i \le n$. Then ${\mathscr {G}}(G)$ is a Gröbner basis of $I_{{\mathscr {A}}_G}$ with respect to a reverse lexicographic order < induced by the ordering $z< x_1< y_1< \cdots< x_n < y_n$ [21, Prop. 3.8]. Here the initial monomial of each binomial is the first monomial. Using this Gröbner basis, we have the following.

Proposition 5.4

Let G be a bipartite graph on [d] and let $e \in E(G)$. Then we have

$$\begin{aligned} h^*({\mathscr {A}}_G, x) = (x+1) h^*({\mathscr {A}}_{G/e}, x). \end{aligned}$$

Proof

Let $E(G)=\{e_1 ,\dots , e_n\}$ with $e = e_1 = \{i,j\}$. Since G is a bipartite graph, the Gröbner basis ${\mathscr {G}}(G)$ above consists of the binomials of the form (1) and (3).

Since G has no triangles, the procedure (ii) does not occur when we contract e of G. Hence $E(G/e) = \{e_2' , \dots , e_n' \}$ where $e_k'$ is obtained from $e_k$ by identifying i with j. Let $G'$ be a graph obtained by adding an edge $e_1' = \{d+1, d+2\}$ to the graph G/e. Then ${\mathscr {G}}(G')$ consists of all binomials f satisfying one of the following:

$$\begin{aligned} f\,=\, \prod _{e_i \in I} p_i - \prod _{e_i \in C \setminus I} q_i, \end{aligned}$$

where C is an even cycle in G of length 2k with a fixed orientation and $e_1 \notin C$, and I is a k-subset of C such that $e_\ell \notin I$ for $\ell = \min {\{i : e_i \in C\}}$;

$$\begin{aligned} f\,=\, \prod _{e_i \in I} p_i \,-\, z\prod _{e_i \in C \setminus I} q_i, \end{aligned}$$

where $C \cup \{e_1\}$ is an even cycle in G of length $2k+2$ and I is a $(k+1)$-subset of C;

$$\begin{aligned} f = x_i y_i - z^2, \end{aligned}$$

where $1 \le i \le n$. Hence $\{ {\text {in}}_< (f) : f \in {\mathscr {G}}(G) \} = \{{\text {in}}_< (f) : f \in {\mathscr {G}}(G') \}$. By a similar argument as in the proof of [19, Thm. 3.1], it follows that

$$\begin{aligned} h^*({\mathscr {A}}_G, x) = h^*( {\mathscr {A}}_{G'}, x) = h^*({\mathscr {A}}_{\{e_1'\}}, x) h^*({\mathscr {A}}_{G/e}, x)= (x+1) h^*({\mathscr {A}}_{G/e}, x) , \end{aligned}$$

as desired. $\square$

From Theorem 5.3, Propositions 5.2 and 5.4 we have the following immediately.

Corollary 5.5

Let G be a bipartite graph on [d]. Then we have that:

• (a) The $h^*$-polynomial $h^*({\mathscr {A}}_{{\widetilde{G}}}, x) = (x+1) h^*({\mathscr {A}}_{{\widehat{G}}}, x)$ is $\gamma$-positive.

• (b) If G is obtained by gluing bipartite graphs $G_1$ and $G_2$ along with an edge e, then

  $$\begin{aligned} h^*({\mathscr {A}}_G, x)&=(x+1) h^*({\mathscr {A}}_{G/e}, x) \\&=(x+1) h^*({\mathscr {A}}_{G_1/e}, x) h^*({\mathscr {A}}_{G_2/e}, x)\\&=h^*({\mathscr {A}}_{G_1}, x) h^*({\mathscr {A}}_{G_2}, x)/(x+1). \end{aligned}$$

Remark

Corollary 5.5 (b) was recently generalized in [8, Thm. 4.17].

5.2 Pseudo-Symmetric Simplicial Reflexive Polytopes

A lattice polytope ${\mathscr {P}}\subset {\mathbb R}^d$ is called pseudo-symmetric if there exists a facet ${\mathscr {F}}$ of ${\mathscr {P}}$ such that $-{\mathscr {F}}$ is also a facet of ${\mathscr {P}}$. Nill [27] proved that any pseudo-symmetric simplicial reflexive polytope ${\mathscr {P}}$ is a free sum of ${\mathscr {P}}_1, \dots , {\mathscr {P}}_s$, where each ${\mathscr {P}}_i$ is one of the following:

• cross polytope;

• del Pezzo polytope $V_{2m} = {\text {conv}}{( \pm {\mathbf{e}}_1,\dots ,\pm {\mathbf{e}}_{2m}, \pm ( {\mathbf{e}}_1 + \dots + {\mathbf{e}}_{2m}) )}$;

• pseudo-del Pezzo polytope ${\widetilde{V}}_{2m} = {\text {conv}}{( \pm {\mathbf{e}}_1,\dots ,\pm {\mathbf{e}}_{2m},-{\mathbf{e}}_1 - \dots - {\mathbf{e}}_{2m} )}$.

Note that a del Pezzo polytope is unimodularly equivalent to ${\mathscr {A}}_{C_{2m+1}}$ where $C_{2m+1}$ is an odd cycle of length $2m+1$ (see [20]). The $h^*$-polynomial of ${\mathscr {A}}_{C_d}$ was essentially studied in the following papers (see also the OEIS sequence A204621):

• Conway and Sloane [6, p. 2379] computed $h^*({\mathscr {A}}_{C_d},x)$ for small d by using results of O’Keeffe [32] and gave a conjecture on the $\gamma$-polynomial of $h^*({\mathscr {A}}_{C_d},x)$ (coincides with the $\gamma$-polynomial in Proposition 5.7 below).

• General formulas for the coefficients of $h^*({\mathscr {A}}_{C_d},x)$ were given in Ohsugi–Shibata [29] and Wang–Yu [40].

In order to give the $h^*$-polynomial of ${\widetilde{V}}_{2m}$, we need the following lemma.

Lemma 5.6

Let G be a connected graph. Suppose that an edge $e=\{i,j\}$ of G is not a bridge. Let ${\mathscr {P}}_e$ be the convex hull of $A(G) \setminus \{ {\mathbf{e}}_i - {\mathbf{e}}_j \}$. Then we have

$$\begin{aligned} h^*({\mathscr {P}}_e,x) = \frac{h^*({\mathscr {A}}_G,x) + h^*({\mathscr {A}}_{G \setminus e},x)}{2}, \end{aligned}$$

where $G \setminus e$ is the graph obtained by deleting e from G.

Proof

Note that ${\mathscr {A}}_{G \setminus e} \subset {\mathscr {P}}_e \subset {\mathscr {A}}_G$. Since G is connected and e is not a bridge of G, the dimension of both ${\mathscr {A}}_G$ and ${\mathscr {A}}_{G \setminus e}$ is $d-1$. Let ${\mathscr {P}}_e'$ denote the convex hull of $A(G) \setminus \{ - {\mathbf{e}}_i + {\mathbf{e}}_j \}$, which is unimodularly equivalent to ${\mathscr {P}}_e$. Then ${\mathscr {A}}_G$ and ${\mathscr {P}}_e$ are decomposed into the following disjoint union:

$$\begin{aligned} {\mathscr {A}}_G&={\mathscr {A}}_{G \setminus e} \cup ({\mathscr {P}}_e \setminus {\mathscr {A}}_{G \setminus e}) \cup ({\mathscr {P}}_e' \setminus {\mathscr {A}}_{G \setminus e}),\\ {\mathscr {P}}_e&={\mathscr {A}}_{G \setminus e} \cup ({\mathscr {P}}_e \setminus {\mathscr {A}}_{G \setminus e}). \end{aligned}$$

Since ${\mathscr {P}}_e \setminus {\mathscr {A}}_{G \setminus e}$ is unimodularly equivalent to ${\mathscr {P}}_e' \setminus {\mathscr {A}}_{G \setminus e}$, we have a desired conclusion. $\square$

The $h^*$-polynomials of $V_{2m}$ and ${\widetilde{V}}_{2m}$ are as follows:

Proposition 5.7

Let $C_d$ denote a cycle of length $d \ge 3$ and let $1 \le m \in {\mathbb Z}$. Then we have

$$\begin{aligned} h^*({\mathscr {A}}_{C_d},x)&= \sum _{i=0}^{\lfloor ({d-1})/{2} \rfloor }\left( {\begin{array}{c}2i\\ i\end{array}}\right) x^i (x+1)^{d-2i-1},\\ h^*(V_{2m},x)&=\sum _{i=0}^m\left( {\begin{array}{c}2i\\ i\end{array}}\right) x^i (x+1)^{2m-2i},\\ h^*({\widetilde{V}}_{2m},x)&= (x+1)^{2m}+ \sum _{i=1}^m\left( {\begin{array}{c}2i-1\\ i-1\end{array}}\right) x^i (x+1)^{2m-2i}. \end{aligned}$$

In particular, the $h^*$-polynomials of ${\mathscr {A}}_{C_d}$, $V_{2m}$, and ${\widetilde{V}}_{2m}$ are $\gamma$-positive.

Proof

The proof for $C_d$ is by induction on d. First, we have $h^*({\mathscr {A}}_{C_{3}},x) = x^2 + 4x +1 = (x+1)^2 + \left( {\begin{array}{c}2\\ 1\end{array}}\right) x$. If $d \ge 4$ is even, then

$$\begin{aligned} h^*({\mathscr {A}}_{C_{d}},x)&= (x + 1) h^*({\mathscr {A}}_{C_{d-1}},x)\\&=\sum _{i=0}^{({d-2})/{2}}\left( {\begin{array}{c}2i\\ i\end{array}}\right) x^i (x+1)^{d-2i-1}\,=\!\sum _{i=0}^{\lfloor ({d-1})/{2} \rfloor }\left( {\begin{array}{c}2i\\ i\end{array}}\right) x^i (x+1)^{d-2i-1}. \end{aligned}$$

Moreover, if $d = 2m +1$, $2 \le m \in {\mathbb Z}$, then the coefficient of $x^m$ in

$$\begin{aligned} \sum _{i=0}^{({d-1})/{2}}\left( {\begin{array}{c}2i\\ i\end{array}}\right) x^i (x+1)^{d-2i-1}= (x+1) h^*({\mathscr {A}}_{C_{d-1}},x)+ \left( {\begin{array}{c}2m\\ m\end{array}}\right) x^m \end{aligned}$$

is

$$\begin{aligned} \sum _{i=0}^m \left( {\begin{array}{c}2i\\ i\end{array}}\right) \left( {\begin{array}{c}2m-2i\\ m-i\end{array}}\right) = 4^m = 2^{d-1}, \end{aligned}$$

and the other coefficient is arising from $(x+1) h^*({\mathscr {A}}_{C_{d-1}},x)$. By a recursive formula in [29, Thm. 2.3], we have

$$\begin{aligned} h^*({\mathscr {A}}_{C_d},x)\,=\! \sum _{i=0}^{({d-1})/{2}}\left( {\begin{array}{c}2i\\ i\end{array}}\right) x^i (x+1)^{d-2i-1}. \end{aligned}$$

Since $V_{2m}$ is unimodularly equivalent to ${\mathscr {A}}_{C_{2m+1}}$, we have $h^*(V_{2m},x) = h^*({\mathscr {A}}_{C_{2m+1}},x)$. By Lemma 5.6, it follows that

$$\begin{aligned} h^*({\widetilde{V}}_{2m},x)&=\frac{h^*({\mathscr {A}}_{C_{2m+1}},x) + h^*({\mathscr {A}}_{P_{2m+1}},x)}{2}\\&=\frac{1}{2} \sum _{i=0}^m\left( {\begin{array}{c}2i\\ i\end{array}}\right) x^i (x+1)^{2m-2i} + \frac{(x+1)^{2m}}{2}\\&=(x+1)^{2m}+ \sum _{i=1}^m\left( {\begin{array}{c}2i-1\\ i-1\end{array}}\right) x^i (x+1)^{2m-2i}. \end{aligned}$$

$\square$

Thus it turns out that any pseudo-symmetric simplicial reflexive polytope is a free sum of reflexive polytopes whose $h^*$-polynomials are $\gamma$-positive. By [4, Thm. 1], we have the following.

Theorem 5.8

The $h^*$-polynomial of any pseudo-symmetric simplicial reflexive polytope is $\gamma$-positive.

Proof

From results by Nill [27], any pseudo-symmetric simplicial reflexive polytope is a free sum of cross polytopes, del Pezzo polytopes, and pseudo-del Pezzo polytopes. On the other hand, by [4, Thm. 1], the $h^*$-polynomial of a free sum of reflexive polytopes ${\mathscr {P}}_1,\ldots ,{\mathscr {P}}_s$ is equal to the product of $h^*$-polynomials of ${\mathscr {P}}_1,\ldots , {\mathscr {P}}_s$. Hence, by Example 5.1 and Proposition 5.7, it follows that the $h^*$-polynomial of any pseudo-symmetric simplicial reflexive polytope is $\gamma$-positive. $\square$

5.3 Classes of Graphs with $h^*({{\mathscr {A}}}_G, x)$ Being $\gamma$-Positive

With the results of the present section one can show that, for example, $h^*({{\mathscr {A}}}_G, x)$ is $\gamma$-positive if one of the following holds:

• $G = {\widehat{H}}$ for some graph H (e.g., G is a complete graph, a wheel graph);

• $G = {\widetilde{H}}$ for some bipartite graph H (e.g., G is a complete bipartite graph);

• G is a cycle;

• G is an outerplanar bipartite graph.

Moreover, one can compute $h^*({{\mathscr {A}}}_G, x)$ explicitly in some cases. We give such calculations for some known formulas (for complete [1] and complete bipartite graphs [21]).

Example 5.9

[1] By Theorem 5.3, we have

$$\begin{aligned} h^*({{\mathscr {A}}}_{K_d}, x) \,=\, h^*({{\mathscr {A}}}_{{\widehat{K}}_{d-1}}, x)\,=\,\frac{(x+1)^{d-1} }{2^{d-2}}\!\! \sum _{H \in {\text {Cut}}(K_{d-1})}\!\! I_{{\widetilde{H}}} \biggl (\frac{4x}{(x+1)^2}\biggr ). \end{aligned}$$

If the edge set of $H \in {\text {Cut}}(K_{d-1})$ is $E_S$ with $S \subset [d-1]$, then H is a complete bipartite graph $K_{|S|, d-1-|S|}$ and

$$\begin{aligned} I_{{\widetilde{H}}}(x) = \sum _{i\ge 0} \left( {\begin{array}{c}|S|\\ i\end{array}}\right) \left( {\begin{array}{c}d-|S|-1\\ i\end{array}}\right) x^i. \end{aligned}$$

(Here $K_{0,d-1}$ denotes an empty graph.) It then follows that

$$\begin{aligned} h^*({{\mathscr {A}}}_{K_d}, x)&=\frac{1}{2^{d-1}}\sum _{k=0}^{d-1}\left( {\begin{array}{c}d-1\\ k\end{array}}\right) \sum _{i = 0}^{\lfloor ({d-1})/{2} \rfloor } 4^i \left( {\begin{array}{c}k\\ i\end{array}}\right) \left( {\begin{array}{c}d-k-1\\ i\end{array}}\right) x^i (x+1)^{d-1-2i}\\&=\frac{1}{2^{d-1}}\sum _{i = 0}^{\lfloor ({d-1})/{2} \rfloor }\!4^i x^i (x+1)^{d-1-2i}\sum _{k=i}^{d-i-1}\left( {\begin{array}{c}d-1\\ k\end{array}}\right) \left( {\begin{array}{c}k\\ i\end{array}}\right) \left( {\begin{array}{c}d-k-1\\ i\end{array}}\right) \\&=\frac{1}{2^{d-1}}\sum _{i = 0}^{\lfloor ({d-1})/{2} \rfloor }\!4^i x^i (x+1)^{d-1-2i}\sum _{k=i}^{d-i-1}\left( {\begin{array}{c}d-1\\ 2i\end{array}}\right) \left( {\begin{array}{c}2i\\ i\end{array}}\right) \left( {\begin{array}{c}d-1-2i\\ k-i\end{array}}\right) \\&=\frac{1}{2^{d-1}}\sum _{i = 0}^{\lfloor ({d-1})/{2} \rfloor }\!4^i x^i (x+1)^{d-1-2i}2^{d-1-2i}\left( {\begin{array}{c}d-1\\ 2i\end{array}}\right) \left( {\begin{array}{c}2i\\ i\end{array}}\right) \\&=\sum _{i = 0}^{\lfloor ({d-1})/{2} \rfloor }\left( {\begin{array}{c}d-1\\ 2i\end{array}}\right) \left( {\begin{array}{c}2i\\ i\end{array}}\right) x^i (x+1)^{d-1-2i} . \end{aligned}$$

Example 5.10

[21]   Let $G=K_{m,n}$. Then ${\widetilde{G}} = K_{m+1,n+1}$ and

$$\begin{aligned} h^*({{\mathscr {A}}}_{K_{m+1,n+1}}, x)&=\,(x+1) h^*({{\mathscr {A}}}_{{\widehat{K}}_{m,n}}, x)\\&= \frac{(x+1)^{m+n+1} }{2^{m+n-1}} \!\!\sum _{H \in {\text {Cut}}(K_{m,n})} \!\! I_{{\widetilde{H}}} \biggl (\frac{4x}{(x+1)^2}\biggr ). \end{aligned}$$

Let $V_1 \cup V_2$ be the partition of the vertex set of $K_{m,n}$, where $|V_1|=m$ and $|V_2|=n$. If the edge set of $H \in {\text {Cut}}(K_{m,n})$ is $E_S$ with $S \subset [m+n]$, then H is the disjoint union of two complete bipartite graphs $K_{k, \ell }$ and $K_{m-k,n-\ell }$, and hence

$$\begin{aligned} I_{{\widetilde{H}}}(x) = \sum _{i\ge 0} \left( {\begin{array}{c}k\\ i\end{array}}\right) \left( {\begin{array}{c}\ell \\ i\end{array}}\right) x^i \times \sum _{j\ge 0} \left( {\begin{array}{c}m-k\\ j\end{array}}\right) \left( {\begin{array}{c}n-\ell \\ j\end{array}}\right) x^j , \end{aligned}$$

where $k=|V_1 \cap S|$ and $\ell = n- |V_2 \cap S|$. It then follows that

$$\begin{aligned} h^*({{\mathscr {A}}}_{K_{m+1,n+1}}, x)&=\frac{x+1}{2^{m+n}}\sum _{k=0}^m\sum _{\ell =0}^n\left( {\begin{array}{c}m\\ k\end{array}}\right) \left( {\begin{array}{c}n\\ \ell \end{array}}\right) \sum _{i=0}^{\min {(k,\ell )}} 4^i \left( {\begin{array}{c}k\\ i\end{array}}\right) \left( {\begin{array}{c}\ell \\ i\end{array}}\right) x^i (x+1)^{k+\ell -2i} \\&\quad \times \sum _{j=0}^{\min {(m-k,n-\ell )}} 4^j \left( {\begin{array}{c}m-k\\ j\end{array}}\right) \left( {\begin{array}{c}n-\ell \\ j\end{array}}\right) x^j (x+1)^{m+n-k-\ell -2j}\\&=\frac{1}{2^{m+n}}\sum _{i,j\ge 0}4^{i+j}x^{i+j} (x+1)^{n+m-2(i+j)+1}\\&\quad \times \sum _{k=i}^{m-j}\left( {\begin{array}{c}m\\ k\end{array}}\right) \left( {\begin{array}{c}k\\ i\end{array}}\right) \left( {\begin{array}{c}m-k\\ j\end{array}}\right) \sum _{\ell =i}^{n-j} \left( {\begin{array}{c}n\\ \ell \end{array}}\right) \left( {\begin{array}{c}\ell \\ i\end{array}}\right) \left( {\begin{array}{c}n-\ell \\ j\end{array}}\right) . \end{aligned}$$

Since

$$\begin{aligned} \sum _{k=i}^{m-j}\left( {\begin{array}{c}m\\ k\end{array}}\right) \left( {\begin{array}{c}k\\ i\end{array}}\right) \left( {\begin{array}{c}m-k\\ j\end{array}}\right)&=\sum _{k=i}^{m-j}\left( {\begin{array}{c}m\\ i+j\end{array}}\right) \left( {\begin{array}{c}i+j\\ i\end{array}}\right) \left( {\begin{array}{c}m-(i+j)\\ k-i\end{array}}\right) \\&=2^{m-(i+j)}\left( {\begin{array}{c}m\\ i+j\end{array}}\right) \left( {\begin{array}{c}i+j\\ i\end{array}}\right) , \end{aligned}$$

we have

$$\begin{aligned} h^*({{\mathscr {A}}}_{K_{m+1,n+1}}, x)&=\sum _{i\ge 0}\sum _{j\ge 0}\left( {\begin{array}{c}i+j\\ i\end{array}}\right) ^{\!2}\left( {\begin{array}{c}m\\ i+j\end{array}}\right) \left( {\begin{array}{c}n\\ i+j\end{array}}\right) x^{i+j }(x+1)^{m+n-2(i+j)+1} \\&=\sum _{\alpha =0}^{\min (m, n)}\sum _{i=0}^\alpha \left( {\begin{array}{c}\alpha \\ i\end{array}}\right) ^{\!2}\left( {\begin{array}{c}m\\ \alpha \end{array}}\right) \left( {\begin{array}{c}n\\ \alpha \end{array}}\right) x^\alpha (x+1)^{m+n-2\alpha +1} \\&=\sum _{\alpha =0}^{\min (m, n)}\left( {\begin{array}{c}2 \alpha \\ \alpha \end{array}}\right) \left( {\begin{array}{c}m\\ \alpha \end{array}}\right) \left( {\begin{array}{c}n\\ \alpha \end{array}}\right) x^\alpha (x+1)^{m+n-2\alpha +1}. \end{aligned}$$

Finally, we conjecture the following:

Conjecture 5.11

The $h^*$-polynomial of any symmetric edge polytope of type A is $\gamma$-positive.

6 Twinned Chain Polytopes

In this section, we will apply Theorem 1.1 to twinned chain polytopes. For two lattice polytopes ${\mathscr {P}}, {\mathscr {Q}}\subset {\mathbb R}^d$, we set

$$\begin{aligned} \Gamma ({\mathscr {P}}, {\mathscr {Q}}):={\text {conv}}{({\mathscr {P}}\cup (- {\mathscr {Q}}))} \subset {\mathbb R}^d. \end{aligned}$$

Let P and Q be two finite posets on [d]. The twinned chain polytope of P and Q is the lattice polytope defined by ${\mathscr {C}}_{P,Q}:=\Gamma ({\mathscr {C}}_P,{\mathscr {C}}_Q)$. Then ${\mathscr {C}}_{P,Q}$ is reflexive. Moreover, ${\mathscr {C}}_{P,Q}$ has a flag, regular unimodular triangulation all of whose maximal simplices contain the origin [16, Prop. 1.2]. Hence we obtain

Corollary 6.1

Let P and Q be two finite posets on [d]. Then the $h^*$-polynomial of ${\mathscr {C}}_{P,Q}$ coincides with the h-polynomial of a flag triangulation of a sphere.

In [39, Prop. 2.2] it was shown that ${\mathscr {C}}_{P,Q}$ is locally anti-blocking. In general, for two finite posets $(P, <_P)$ and $(Q,<_Q)$ with $P \cap Q = \emptyset$, the ordinal sum of P and Q is the poset $(P \oplus Q, <_{P \oplus Q})$ on $P \oplus Q= P \cup Q$ such that $i <_{P \oplus Q} j$ if and only if (a) $i,j \in P$ and $i <_P j$, or (b) $i,j \in Q$ and $i <_Q j$, or (c) $i \in P$ and $j \in Q$. Given a subset I of [d], we define the induced subposet of P on I to be the finite poset $(P_I,<_{P_I})$ on I such that $i <_{P_I} j$ if and only if $i <_P j$. For $I \subset [d]$, let ${\overline{I}}:=[d] \setminus I$.

Proposition 6.2

[39, Prop. 2.2] Let P and Q be two finite posets on [d]. Then for each $\varepsilon \in \{-1,1\}^d$, it follows that

$$\begin{aligned} {\mathscr {C}}_{P,Q} \cap {\mathbb R}^d_{\varepsilon }={\mathscr {C}}^{\pm }_{P_{I_\varepsilon } \oplus Q_{\overline{I_{\varepsilon }}}} \cap {\mathbb R}^d_{\varepsilon }, \end{aligned}$$

where $I_{\varepsilon }=\{i \in [d] : \varepsilon _i=1 \}$.

From this result, Theorem 1.1, and Proposition 3.4 we obtain the following:

Theorem 6.3

Let P and Q be two finite posets on [d]. Then one has

$$\begin{aligned} h^*({\mathscr {C}}_{P,Q}, x)\,=\, \frac{1}{2^{d}}\sum _{\varepsilon \in \{-1,1\}^d}\!\!h^*({\mathscr {C}}^{(e)}_{R_{\varepsilon }},x)\,=\,(x+1)^d f_{P,Q}\biggl ( \frac{4x}{(x+1)^2} \biggr ), \end{aligned}$$

where $I_{\varepsilon }=\{i \in [d] : \varepsilon _i=1 \}$ and $R_{\varepsilon }$ is a naturally labeled poset that is obtained from $P_{I_\varepsilon } \oplus Q_{{\overline{I}}_{\varepsilon }}$ by reordering the label and

$$\begin{aligned} f_{P,Q}(x)=\frac{1}{2^{d}}\sum _{\varepsilon \in \{-1,1\}^d}\!\!W^{(\ell )}_{R_{\varepsilon }}(x). \end{aligned}$$

In particular, $h^*({\mathscr {C}}_{P,Q},x)$ is $\gamma$-positive. Moreover, $h^*({\mathscr {C}}_{P,Q},x)$ is real-rooted if and only if $f_{P,Q}(x)$ is real-rooted.

On the other hand, it is known that from $h^*({\mathscr {C}}_{P,Q},x)$ we obtain $h^*$-polynomials of several non-locally anti-blocking lattice polytopes arising from the posets P and Q. The order polytope ${\mathscr {O}}_P$ [37] of P is the (0, 1)-polytope defined by

$$\begin{aligned} {\mathscr {O}}_P:=\{ {\mathbf{x}}\in [0,1]^d : x_i \le x_j\ \text {if}\ i <_P j \}. \end{aligned}$$

Given two lattice polytopes ${\mathscr {P}}, {\mathscr {Q}}\subset {\mathbb R}^d$, we define

$$\begin{aligned} {\mathscr {P}}*{\mathscr {Q}}:={\text {conv}}{ (({\mathscr {P}}\times \{0\}) \cup ({\mathscr {Q}}\times \{1\}) ) }\subset {\mathbb R}^{d+1}, \end{aligned}$$

which is called the Cayley sum of ${\mathscr {P}}$ and ${\mathscr {Q}}$, and define

$$\begin{aligned} \Omega ({\mathscr {P}},{\mathscr {Q}}):={\text {conv}}{(({\mathscr {P}}\times \{1\}) \cup (-{\mathscr {Q}}\times \{-1\}) )} \subset {\mathbb R}^{d+1}. \end{aligned}$$

Proposition 6.4

[16, Thm. 1.1] Let P and Q be two finite posets on [d]. Then

$$\begin{aligned}h^*({\mathscr {C}}_{P,Q},x)=h^*(\Gamma ({\mathscr {O}}_P,{\mathscr {C}}_Q),x).\end{aligned}$$

Furthermore, if P and Q have a common linear extension, then

$$\begin{aligned}h^*({\mathscr {C}}_{P,Q},x)=h^*(\Gamma ({\mathscr {O}}_P,{\mathscr {O}}_Q),x).\end{aligned}$$

Proposition 6.5

[18, Thm. 1.4] Let P and Q be two finite posets on [d]. Then

$$\begin{aligned}(1+x)h^*({\mathscr {C}}_{P,Q},x)=h^*(\Omega ({\mathscr {O}}_P,{\mathscr {C}}_Q),x).\end{aligned}$$

Furthermore, if P and Q have a common linear extension, then

$$\begin{aligned} (1+x)h^*({\mathscr {C}}_{P,Q},x)=h^*(\Omega ({\mathscr {O}}_P,{\mathscr {O}}_Q),x).\end{aligned}$$

Proposition 6.6

[17, Thm. 4.1] Let P and Q be two finite posets on [d]. Then

$$\begin{aligned}h^*({\mathscr {C}}_{P,Q},x)=h^*({\mathscr {O}}_P * {\mathscr {C}}_Q,x).\end{aligned}$$

From these propositions and Theorem 6.3, we obtain the following:

Corollary 6.7

Let P and Q be two finite posets on [d]. Then the $h^*$-polynomials of $\Gamma ({\mathscr {O}}_P,{\mathscr {C}}_Q)$, $\Omega ({\mathscr {O}}_P, {\mathscr {C}}_Q)$, ${\mathscr {O}}_P*{\mathscr {C}}_Q$, and $\Omega ({\mathscr {C}}_P,{\mathscr {C}}_Q)$ are $\gamma$-positive. Furthermore, if P and Q have a common linear extension, then the $h^*$-polynomials of $\Gamma ({\mathscr {O}}_P,{\mathscr {O}}_Q)$ and $\Omega ({\mathscr {O}}_P,{\mathscr {O}}_Q)$ are also $\gamma$-positive.

In the rest of this section, we introduce enriched (P, Q)-partitions and we show that the Ehrhart polynomial of ${\mathscr {C}}_{P,Q}$ coincides with a counting polynomial of enriched (P, Q)-partitions. Assume that P and Q are naturally labeled. We say that a map $f :[d] \rightarrow {\mathbb Z}$ is an enriched (P, Q)-partition if, for all $x, y \in [d]$, it satisfies

• $x <_P y$, $f(x) \ge 0$, and $f(y) \ge 0 \Rightarrow f(x) \le f(y)$;

• $x <_Q y$, $f(x) \le 0$, and $f(y) \le 0 \Rightarrow f(x) \ge f(y)$.

For a map $f :[d] \rightarrow {\mathbb Z}$, we set

$$\begin{aligned} m(f) = \min { \{ \{0\} \cup \{ f(x) : x \in [d] \} \}}\quad \text {and}\quad M(f) = \max {\{ \{0\} \cup f(x) : x \in [d]\} \}}. \end{aligned}$$

For each $0 < m \in {\mathbb Z}$, let $\Omega _{P,Q}^{(e)}(m)$ denote the number of enriched (P, Q)-partitions $f:[d] \rightarrow {\mathbb Z}$ with $M(f) - m(f) \le m$.

Theorem 6.8

Let P and Q be two finite posets on [d]. Then one has

$$\begin{aligned} L_{{\mathscr {C}}_{P,Q}}(m)=\Omega _{P,Q}^{(e)}(m). \end{aligned}$$

Proof

Let F(m) stand for the set of enriched (P, Q)-partitions with $M(f)- m(f) \le m$. We show that there exists a bijection from $m{\mathscr {C}}_{P,Q} \cap {\mathbb Z}^d$ to F(m). Take $f \in F(m)$ and set $m(f) = a$ and $M(f)=b$. We set

$$\begin{aligned} I=\{i \in [d] : f(i) \ge 0 \}. \end{aligned}$$

Let

$$\begin{aligned} x_i={\left\{ \begin{array}{ll} f(i) &{}\quad \text {if }i \in I\text { is minimal in} \ P_I,\\ \min { \{ f(i) -f(j) : i\ \text {covers}\ j\ \text {in}\ P_I\}} &{}\quad \text {if }i \in I\text { is not minimal in }P_I,\\ -|f(i)| &{}\quad \text {if }i \in {\overline{I}}\text { is minimal in }Q_{{\overline{I}}},\\ -\min { \{ |f(i)| -|f(j)| : i\ \text {covers}\ j\ \text {in}\ Q_{{\overline{I}}}\}}&{}\quad \text {if }i\in {\overline{I}}\text { is not minimal in }Q_{{\overline{I}}}. \end{array}\right. } \end{aligned}$$

Assume that $I=\{1,\ldots ,k \}$ and ${\overline{I}}=\{k+1,\ldots ,d\}$. Then we have $(x_1,\ldots ,x_k) \in b {\mathscr {C}}_{P_I}$ and $(x_{k+1},\ldots ,x_d) \in a{\mathscr {C}}_{Q_{{\overline{I}}}}$ by a result of Stanley [37, Thm. 3.2]. Hence one obtains $(x_1,\ldots ,x_d) \in b {\mathscr {C}}_{P_I} \oplus a {\mathscr {C}}_{Q_{{\overline{I}}}} \subset m{\mathscr {C}}_{P,Q}$, where $b {\mathscr {C}}_{P_I} \oplus a {\mathscr {C}}_{Q_{{\overline{I}}}}$ is the free sum of $b {\mathscr {C}}_{P_I}$ and $a {\mathscr {C}}_{Q_{{\overline{I}}}}$. Similarly, in general, it follows that $(x_1,\ldots ,x_d) \in m{\mathscr {C}}_{P,Q}$. Therefore, the map $\varphi :F(m) \rightarrow m {\mathscr {C}}_{P,Q} \cap {\mathbb Z}^d$, $\varphi (f)=(x_1,\ldots ,x_d)$ for each $f \in F(m)$, is well defined.

Take $(x_1,\ldots ,x_d) \in m{\mathscr {C}}_{P,Q} \cap {\mathbb Z}^d$. We set $I= \{ i \in [d] : x_i \ge 0 \}$ and define a map $f:[d] \rightarrow {\mathbb Z}$ by

$$\begin{aligned} f(i) ={\left\{ \begin{array}{ll} \max {\{x_{j_1} + \dots + x_{j_k} : j_1<_{P_I} \cdots<_{P_I} j_k =i \}} &{}\quad \text {if }i \in I,\\ -\max {\{ |x_{j_1}| + \dots + |x_{j_k}| : j_1<_{Q_{{\overline{I}}}} \cdots <_{Q_{{\overline{I}}}} j_k =i \}} &{}\quad \text {if }i \in {\overline{I}}. \end{array}\right. } \end{aligned}$$

Assume that $I=\{1,\ldots ,k \}$ and ${\overline{I}}=\{k+1,\ldots ,d\}$. Then one has $(x_1,\ldots ,x_d) \in m({\mathscr {C}}_{P_I} \oplus (-{\mathscr {C}}_{Q_{{\overline{I}}}})) \cap {\mathbb Z}^d$. Moreover, for some integers a and b with $a \le 0 \le b$ and $b-a \le m$, it follows that $(x_1,\ldots ,x_k) \in b {\mathscr {C}}_{P_I}$ and $(x_{k+1},\ldots ,x_d) \in a {\mathscr {C}}_{Q_{{\overline{I}}}}$. We define $f_1:I \rightarrow {\mathbb Z}$ by $f_1(i)=f(i)$, and $f_2:{\overline{I}} \rightarrow {\mathbb Z}$ by $f_2(i)=-f(i)$. From [37, proof of Thm. 3.2], it follows that $0 \le f_1(i) \le b$ for any $i \in I$ and $f_1(x) \le f_1(y)$ if $x_{<_{P_I}} y$, and $0 \ge f_2(i) \ge a$ for any $i \in {\overline{I}}$ and $f_2(x) \le f_2(y)$ if $x_{<_{Q_{{\overline{I}}}}} y$. Therefore, $f:[d] \rightarrow {\mathbb Z}$ is an enriched (P, Q)-partition with $M(f)-m(f) \le b - a \le m$, namely, $f \in F(m)$. Similarly, in general, it follows that $f \in F(m)$. Thus, the map $\psi :m{\mathscr {C}}_{P,Q} \cap {\mathbb Z}^d \rightarrow F(m)$, $\psi ({\mathbf{x}})(i)=f(i)$ for each ${\mathbf{x}}=(x_1,\ldots ,x_d) \in m{\mathscr {C}}_{P,Q} \cap {\mathbb Z}^d$, is well defined.

Finally, we show that $\varphi$ is a bijection. However, this immediately follows by the above and the argument in [37, proof of Thm. 3.2]. $\square$

Since ${\mathscr {C}}_{P,Q}$ is reflexive, we obtain

Corollary 6.9

Let P and Q be two finite naturally labeled posets on [d]. Then $\Omega ^{(e)}_{P,Q}(m)$ is a polynomial in m of degree d and one has

$$\begin{aligned} \Omega ^{(e)}_{P,Q}(m)=(-1)^d\Omega ^{(e)}_{P,Q}(-m-1). \end{aligned}$$