Smooth Fano Polytopes with Many Vertices

Abstract

The $d$-dimensional simplicial, terminal, and reflexive polytopes with at least $3d-2$ vertices are classified. In particular, it turns out that all of them are smooth Fano polytopes. This improves on previous results of Casagrande (Ann Inst Fourier (Grenoble) 56(1):121–130, 2006) and Øbro (Manuscr Math 125(1): 69–79, 2008). Smooth Fano polytopes play a role in algebraic geometry and mathematical physics.

1 Introduction

A lattice polytope $P$ is a convex polytope whose vertices lie in a lattice $N$ contained in the vector space ${\mathbb {R}}^d$. Fixing a basis of $N$ describes an isomorphism to ${\mathbb {Z}}^d$. Throughout this paper, we restrict our attention to the standard lattice $N={\mathbb {Z}}^d$. A $d$-dimensional lattice polytope $P\subset {\mathbb {R}}^d$ is called reflexive if it contains the origin $\mathbf 0$ as an interior point and its polar polytope is a lattice polytope in the dual lattice $M{:}{=}{{\mathrm{Hom}}}(N,{\mathbb {Z}})\cong {\mathbb {Z}}^d$. A lattice polytope $P$ is terminal if $\mathbf 0$ and the vertices are the only lattice points in $P\cap {\mathbb {Z}}^d$. It is simplicial if each face is a simplex. We say that $P$ is a smooth Fano polytope if $P\subseteq {\mathbb {R}}^d$ is simplicial with $\mathbf 0$ in the interior and the vertices of each facet form a lattice basis of ${\mathbb {Z}}^d$. The fan where every cone is the non-negative linear span over a face is called the face fan. It is dual to the normal fan, which is the collection of all normal cones.

In algebraic geometry, reflexive polytopes correspond to Gorenstein toric Fano varieties. The toric variety $X_P$ of a polytope $P$ is determined by the face fan of $P$, that is, the fan spanned by all faces of $P$; see Ewald [10] or Cox et al. [8] for more details. The toric variety $X_P$ is ${\mathbb {Q}}$ -factorial (some multiple of a Weil divisor is Cartier) if and only if the polytope $P$ is simplicial. In this case the Picard number of $X$ equals $n-d$, where $n$ is the number of vertices of $P$. The polytope $P$ is smooth if and only if the variety $X_P$ is a manifold (that is, it has no singularities). Note that the notions detailed above are not entirely standardized in the literature. For example, our definitions agree with [16], but disagree with [12]. Our main result, Theorem 7, is the following.

Theorem

Any $d$-dimensional simplicial, terminal, and reflexive lattice polytope with at least $3d-2$ vertices is lattice equivalent to a direct sum of del Pezzo polytopes, pseudo del Pezzo polytopes, or a (possibly skew and multiple) bipyramid over (pseudo) del Pezzo polytopes. In particular, such a polytope is necessarily smooth Fano.

This extends results of Casagrande who proved that the number of vertices of $d$-dimensional simplicial, terminal, and reflexive lattice polytopes does not exceed $3d$ and who showed that, up to lattice equivalence, only one type exists which attains this bound (and the dimension $d$ is even) [7]. Moreover, our result extends results of Øbro who classified the polytopes of the named kind with $3d-1$ vertices [20]. Our proof employs techniques similar to those used by Øbro [20] and Nill and Øbro [18], but requires more organization since a greater variety of possibilities occurs. One benefit of our approach is that it suggests a certain general pattern emerging, and we state this as Conjecture 9 below. Translated into the language of toric varieties our main result establishes that any $d$-dimensional terminal ${\mathbb {Q}}$-factorial Gorenstein toric Fano variety with Picard number at least $2d-2$ decomposes as a (possibly trivial) toric fiber bundle with known fiber and base space; the precise statement is Corollary 10.

The interest in such classifications has its origins in applications of algebraic geometry to mathematical physics. For instance, Batyrev [2] uses reflexive polytopes to construct pairs of mirror symmetric Calabi–Yau manifolds; see also Batyrev and Borisov [4]. Up to unimodular equivalence, there exists only a finite number of such polytopes in each dimension, and they have been classified up to dimension $4$, see Batyrev [1], Kreuzer and Skarke [13, 14]. Smooth reflexive polytopes have been classified up to dimension $8$ by Øbro [19]; see [5] for data. By enhancing Øbro ’s implementation within the polymake framework [11] this classification was extended to dimension 9 [15]; from that site the data is available in polymake format.

2 Lattice Polytopes

Let $N\cong {\mathbb {Z}}^d$ be a lattice with associated real vector space $N_{\mathbb {R}}\,{:}{=}\,N\otimes _{\mathbb {Z}}{\mathbb {R}}$ isomorphic to ${\mathbb {R}}^d$. The lattice $M\,{:}{=}\,{{\mathrm{Hom}}}_{\mathbb {Z}}(N,{\mathbb {Z}})\cong {\mathbb {Z}}^d$ is dual to $N$ with dual vector space $M_{\mathbb {R}}=M\otimes _{\mathbb {Z}}{\mathbb {R}}\cong {\mathbb {R}}^d$. A polytope $P\subset {\mathbb {R}}^d$ is a lattice polytope with respect to $N$ if its vertex set $\mathrm{Vert }(P)$ is contained in $N$. If the polytope $P$ is full-dimensional and contains the origin $\mathbf 0$ as an interior point, then the polar

$$\begin{aligned} P^* = \{ w\in {\mathbb {R}}^d | \langle v,w\rangle \le 1 \text { for all } v\in P \} \end{aligned}$$

is a convex $d$-polytope, too, which also contains the origin as an interior point. We always have ${(P^*)}^*=P$. However, in general, the polar of a lattice polytope is not a lattice polytope. If $P$ is a lattice polytope in $M$ and the vertices of $P^*$ are contained in $M$, then the polytopes $P$ and $P^*$ are called reflexive. The lattice polytope $P$ is terminal if $P\cap N=\mathrm{Vert }(P)\cup \{\mathbf 0\}$. More generally, $P$ is canonical if the origin is the only interior lattice point in $P$. Two lattice polytopes are lattice equivalent if one can be mapped to the other by a transformation in $\mathrm GL _{d}{{\mathbb {Z}}}$ followed by a lattice translation. Throughout the paper we assume that our polytopes lie in the standard lattice $N={\mathbb {Z}}^d$.

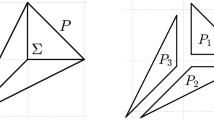
We start out with listing all possible types of $2$-dimensional terminal and reflexive lattice polytopes in Fig. 1. Up to lattice equivalence five cases occur which we denote as $P_6, P_5, P_{4a}, P_{4b}$, and $P_3$, respectively; one hexagon, one pentagon, two quadrangles, and a triangle; see Ewald [10, Thm. 8.2]. All of them are smooth Fano polytopes, that is, the origin lies in the interior and the vertex set of each facet forms a lattice basis. The only $1$-dimensional reflexive polytope is the interval $[-1,1]$. See Cox et al. [8, p. 382] for the classification of all $2$-dimensional reflexive polytopes (of which there are 16 types).

Fig. 1

The $2$-dimensional reflexive and terminal lattice polytopes

Let $P\subset {\mathbb {R}}^d$ and $Q\subset {\mathbb {R}}^e$ be polytopes with the origin in their respective relative interiors. Then the polytope

$$\begin{aligned} P\oplus Q = {{\mathrm{conv}}}(P\cup Q) \quad \subset \ {\mathbb {R}}^{d+e} \end{aligned}$$

is the direct sum of $P$ and $Q$. This construction also goes by the name “linear join” of $P$ and $Q$. Clearly, forming direct sums is commutative and associative. Notice that the polar polytope $(P\oplus Q)^*=P^*\times Q^*$ is the direct product. An important special case is the proper bipyramid $[-1,1]\oplus Q$ over $Q$. More generally, we call a polytope $B$ a (skew) bipyramid over $Q$ if $Q$ is contained in an affine hyperplane $H$ such that there are two vertices $v$ and $w$ of $B$ which lie on either side of $H$ such that $B={{\mathrm{conv}}}(\{v,w\}\cup Q)$ and the line segment $[v,w]$ meets $Q$ in its (relative) interior. The relevance of these constructions for simplicial, terminal, and reflexive polytopes stems from the following three basic facts; see also [10, §V.7.7] and Fig. 2 below. We include a short proof for the sake of completeness.

Fig. 2

The $3$-dimensional smooth Fano polytopes with $3d-1=8$ vertices. Combinatorially, both are bipyramids over $P_6$

Lemma 1

Let $P\subset {\mathbb {R}}^d$ and $Q\subset {\mathbb {R}}^e$ both be lattice polytopes. Then the direct sum $P\oplus Q\subset {\mathbb {R}}^{d+e}$ is simplicial, terminal, or reflexive if and only if $P$ and $Q$ are.

Proof

We check the three properties separately. Faces of a direct sum are convex hulls of faces of the summands, so $P\oplus Q$ is simplicial if and only if $P$ and $Q$ are.

The direct sum $P\oplus Q$ contains $\mathbf 0$ by construction. The direct product $(P\oplus Q)^* = P^*\times Q^*$ is integral if and only if both $P^*$ and $Q^*$ are, so if and only if $P$ and $Q$ are reflexive.

Finally, if $P$ is not terminal, then there is a non-zero lattice point $x$ in $P$ which is not a vertex. By definition of $P\oplus Q$ we have $(x,0)\in P\oplus Q$, and this is not a vertex. So the sum is not terminal. Conversely, if $P\oplus Q$ is not terminal, then there is $y\in (P\oplus Q)\cap Z^{d+e}\setminus \{\mathbf 0\}$ which is not a vertex of $P\oplus Q$. We can write $y=\lambda p+\mu q$ for points $p\in P, q\in Q$ and $\lambda , \mu \ge 0$ with $\lambda +\mu =1$. We can assume that $p,q\ne 0$. But $p$ and $q$ are in orthogonal subspaces, so $\lambda p\in P\cap {\mathbb {Z}}^d$ and $\mu q\in Q\cap {\mathbb {Z}}^e$. So $\lambda =1$ and $\mu =0$, or vice versa. $\square$

Since the interval $[-1,1]$ is simplicial, terminal, and reflexive we arrive at the following direct consequence.

Lemma 2

Let $P=[-1,1]*Q$ be a proper bipyramid over a $(d{-}1)$-dimensional lattice polytope $Q$. Then $P$ is simplicial, terminal or reflexive if and only if $Q$ has the corresponding property.

In our proofs below we will frequently encounter the following situation. Let $Q$ be a $(d{-}1)$-dimensional lattice polytope embedded in $\{\mathbf 0\}\times {\mathbb {R}}^{d-1}\subset {\mathbb {R}}^d$, let $e_1$ be the first standard basis vector of ${\mathbb {R}}^d$, and let $v$ be a vertex of $Q$ such that the line segment ${{\mathrm{conv}}}\{e_1,v-e_1\}$ intersects $Q$ in the relative interior. This is to say that $P{:}{=}{{\mathrm{conv}}}(\{e_1,v-e_1\}\cup Q)\subset {\mathbb {R}}^d$ is a skew bipyramid over $Q$. In this case an argument similar to the proof of Lemma 1 yields a suitable variation of Lemma 2.

Lemma 3

The skew bipyramid $P$ is simplicial, terminal or reflexive if and only if $Q$ has the corresponding property.

Proof

As in the proof of Lemma 1 we check the three properties one by one.

The facets of $P$ are pyramids over facets of $Q$. A pyramid is a simplex if and only if its base is a simplex of one dimension lower. This means that $P$ is simplicial if and only if $Q$ is.

A copy of $Q$ arises as the intersection of $P$ with the coordinate subspace, $H$, spanned by $e_2,e_3,\ldots ,e_d$. Hence the terminality of $P$ implies the terminality of $Q$. Conversely, assume that $Q$ is terminal. Any non-vertex lattice point of $P$ would have to lie outside the hyperplane $H$. Yet, by construction, the only two vertices outside $H$ are at levels $1$ and $-1$; so there is no room for any lattice point in $P$ other than the origin.

Let us assume that the origin is an interior lattice point of $Q$. Then each facet $G$ of $Q$ has a uniquely determined outer facet normal vector $u_G$ such that an inequality which defines $G$ reads $\langle u_G,x\rangle \le 1$. We call this the standard outer facet normal vector of $G$. If $F={{\mathrm{conv}}}(G\cup \{v-e_1\})$ is a facet of $P$ which arises as a pyramid over $G$ then the standard outer facet normal vector $u_F$ satisfies

$$\begin{aligned} \langle u_F,e_1\rangle = \langle u_G,v\rangle - 1 \quad \text {and} \quad \langle u_F,e_j\rangle = \langle u_G,e_j\rangle \text { for all } j\ge 2 \,. \end{aligned}$$

This shows that $u_F$ is integral if and only $u_G$ is. For the remaining facets of $P$, all of which contain $e_1$, the vertex antipodal to $v-e_1$, we have $\langle u_F,e_1\rangle =-1$. Therefore, $P$ is reflexive if and only if $Q$ is. $\square$

Let $e_1,e_2, \ldots , e_d$ be the standard basis of ${\mathbb {Z}}^d$ in ${\mathbb {R}}^d$. The $d$-polytopes

$$\begin{aligned} \mathrm{DP }(d) = {{\mathrm{conv}}}\{\pm e_1,\pm e_2, \ldots , \pm e_d, \pm \mathbf 1\} \quad \subset \ {\mathbb {R}}^d \end{aligned}$$

for $d$ even with $2d+2$ vertices form a $1$-parameter family of smooth Fano polytopes; see Ewald [10, §V.8.3]. They are usually called del Pezzo polytopes. If $-\mathbf 1$ is not a vertex the resulting polytopes are sometimes called pseudo del Pezzo. Here and throughout we abbreviate $\mathbf 1=(1,1,\ldots ,1)$. Notice that the $2$-dimensional del Pezzo polytope $\mathrm{DP }(2)$ is lattice equivalent to the hexagon $P_6$ shown in Fig. 1, and the $2$-dimensional pseudo del Pezzo polytope is the pentagon $P_5$. While the definition of $\mathrm{DP }(d)$ also makes sense in odd dimensions, these polytopes are not simplicial if $d\ge 3$ is odd.

For centrally symmetric smooth Fano polytopes Voskresenskiĭ and Klyachko [21] provide a classification result. They showed that every centrally symmetric smooth Fano polytope can be written as a sum of line segments and del Pezzo polytopes. Later Ewald [9, 10] generalized this classification for pseudo-symmetric polytopes. A polytope is pseudo-symmetric if there exists a facet $F$, such that $-F = \left\{ -v\,\right. \left| \,v\in F\right\}$ is also a facet. Nill [17] extended Ewald’s result to simplicial reflexive polytopes.

Theorem 4

(Nill [17, Thm. 0.1]) Any pseudo-symmetric simplicial and reflexive polytope is lattice equivalent to a direct sum of a centrally symmetric reflexive cross polytope, del Pezzo polytopes, and pseudo del Pezzo polytopes.

A direct sum of $d$ intervals $[-1,1]\oplus [-1,1]\oplus \cdots \oplus [-1,1]$ is the same as the regular cross polytope ${{\mathrm{conv}}}\{\pm e_1,\pm e_2,\ldots ,\pm e_d\}$, which is centrally symmetric and reflexive. The direct sum of several intervals with a polytope $Q$ is the same as an iterated proper bipyramid over $Q$.

Theorem 5

(Casagrande [7, Thm. 3]) A simplicial and reflexive $d$-polytope $P$ has at most $3d$ vertices. If it does have exactly $3d$ vertices then $d$ is even, and $P$ is a centrally symmetric smooth Fano polytope. Thus in this case $P$ is lattice equivalent to a direct sum of $\frac{d}{2}$ copies of $P_6\cong \mathrm{DP }(2)$.

Øbro classified the simplicial, terminal, and reflexive $d$-polytopes with $3d-1$ vertices [20]. We describe the cases which occur, again up to lattice equivalence. To get an idea it is instrumental to look at the low-dimensional cases first. For instance, the interval $[-1,1]$ is of this kind since it has the right number $3\cdot 1-1=2$ vertices. In dimension two we only have the pentagon $P_5$. In dimension three two cases arise which are combinatorially isomorphic but inequivalent as lattice polytopes: the proper bipyramid $[-1,1]\oplus P_6$, which has the vertices

$$\begin{aligned} \pm e_1, \pm e_2, \pm e_3, \pm (e_2-e_3) \end{aligned}$$

and the skew bipyramid over $P_6$ with vertices

$$\begin{aligned} e_1, \pm e_2, \pm e_3,\pm (e_2-e_3), e_3-e_1 ; \end{aligned}$$

see Fig. 2. The apices of the proper bipyramid are $\pm e_1$, and in the skew bipyramid the vertices $e_1$ and $e_3-e_1$ form the apices.

By forming suitable direct sums we can construct more smooth Fano $d$-polytopes with $3d-1$ vertices. For $d$ even the polytope $P_5 \oplus P_6^{\oplus \big (\frac{d}{2}-1\big )}$ is $d$-dimensional, and it has $3d-1$ vertices. Up to a lattice isomorphism these can be chosen as follows.

$$\begin{aligned}&\quad \quad \quad \quad \quad \quad \quad e_1,\pm e_2, \ldots ,\pm e_{d}, \nonumber \\&\pm (e_1-e_2),\ \pm (e_3-e_4),\ldots ,\pm (e_{d-1} - e_{d}) \,. \end{aligned}$$

(1)

For an odd number $d$ we can sum up $\frac{d-1}{2}$ copies of $P_6$ and form the bipyramid. The resulting $d$-dimensional polytope has the vertices

$$\begin{aligned}&\quad \quad \quad \quad \quad \quad \quad \pm e_1,\pm e_2, \ldots ,\pm e_{d}, \nonumber \\&\pm (e_2-e_3),\pm (e_4-e_5),\ldots ,\ \pm (e_{d-1} - e_{d}). \end{aligned}$$

(2)

Notice that the eight vertices $\pm e_1,\pm e_{d-1},\pm e_d,\pm (e_{d-1}-e_d)$ form a 3-dimensional bipyramid $[-1,1]\oplus P_6$. Replacing this summand by a three dimensional skew bipyramid over $P_6$ yields a polytope with vertices

$$\begin{aligned}&\quad \quad \quad \quad \quad \quad \quad \quad \pm e_1, \pm e_2, \ldots ,\pm e_{d-1}, e_{d}, \nonumber \\&\pm (e_1-e_2),\pm (e_3-e_4),\ldots ,\pm (e_{d-2} - e_{d-1}), (e_1 - e_{d}). \end{aligned}$$

(3)

Theorem 6

(Øbro [20, Thm. 1]) A simplicial, terminal, and reflexive lattice $d$-polytope with exactly $3d-1$ is lattice equivalent to the polytope (1) if $d$ is even, and it is lattice equivalent to either (2) or (3) if $d$ is odd.

It turns out that all these polytopes are smooth Fano. Note that there even exists a generalization without the terminality assumption; see Nill and Øbro [18]. From this classification it follows that combinatorially only one case per dimension occurs. This is a consequence of the fact that a proper bipyramid is combinatorially equivalent to a skew bipyramid.

Our main result is the following classification. A double bipyramid is a bipyramid over a bipyramid, and each of these bipyramids can be proper or skew.

Theorem 7

Any $d$-dimensional simplicial, terminal, and reflexive polytope $P$ with exactly $3d-2$ vertices is lattice equivalent to one of the following. If $d$ is even then $P$ is lattice equivalent to

• (i) a double proper or skew bipyramid over $P_6^{\oplus \frac{d-2}{2}}$ or

• (ii) $P_5^{\oplus 2} \oplus P_6^{\oplus \big (\frac{d}{2} - 2\big )}$ or

• (iii) $\mathrm{DP }(4) \oplus P_6^{\oplus \big (\frac{d}{2} - 2\big )}$.

If $d$ is odd then $P$ is lattice equivalent to

• (iv) a proper or skew bipyramid over $P_5 \oplus P_6^{\oplus \frac{d-3}{2}}$.

In particular, if $d$ is even there are three combinatorial types, and the combinatorial type is unique if $d$ is odd. Moreover, $P$ is a smooth Fano polytope in all cases.

Remark 8

The cases above split into several lattice isomorphism classes, which we want to enumerate explicitly. For this, observe that up to lattice equivalence any bipyramid over a simplicial, terminal, and reflexive polytope $Q\subseteq {\mathbb {R}}^{d-1}\times \{0\}$ can be realized as ${{\mathrm{conv}}}(Q\cup \{e_d, -e_d+v\})$, where $v$ is a vertex of $Q$ or zero. Hence, up to lattice equivalence, each proper or skew bipyramid can be described by specifying $v$. The case $v=0$ is the proper bipyramid. A double proper or skew bipyramid is then given by a pair of points.

Suppose first that $d$ is even. Any even-dimensional simplicial, terminal, and reflexive polytope with $3d-2$ vertices is lattice equivalent to $Q\oplus P_6^{\oplus k}$ for a simplicial, terminal, and reflexive polytope $Q$ of (even) dimension at most $6$, and $k=\frac{d-\dim Q}{2}$. Hence, it suffices to classify up to dimension $6$. This will be explained in the following paragraph.

The two planar variants are shown in Fig. 1c, d. For $d=4$ the case (i) splits into eight subtypes, depending on the choice of the two apices of the bipyramid. Let $v_1, v_2, \ldots , v_6$ be the vertices of $P_6$ in cyclic order, and $x,x'$ the apices of the first bipyramid. Then we have the following choices:

$$\begin{aligned} (0,0),\quad (0,x),\quad (0,v_1),\quad (v_1,v_1),\quad (v_1, v_2),\quad (v_1,v_3),\quad (v_1,v_4),\quad \text {and}\quad (v_1,x). \end{aligned}$$

The reason is that the group of lattice automorphisms of $P_6$, which is isomorphic to the dihedral group of order 12, acts sharply transitively on adjacent pairs of vertices. The two types (i) and (ii) don’t split further into lattice isomorphism types. In dimension $d=6$ we have one additional choice for the apices of a double skew bipyramid: We can choose the vertices in distinct hexagons. Summarizing, in even dimensions there are eleven lattice isomorphism types in dimensions $d\ge 6$, ten for $d=4$ and two for $d=2$.

Now let us look at the odd dimensional cases. For $d=1$ we have the segment $[-1,1]$, and for $d=3$ there are the proper and skew bipyramid over $P_5$. Let $w_1, w_2, \ldots , w_5$ be the vertices of $P_5$ in cyclic order, and $w_1$ is the unique vertex such that $-w_1$ is not a vertex of $P_5$. For bipyramids in dimensions $d\ge 5$ we can choose $v$ as $0, w_1, w_2, w_3, v_1$, which gives us all five possible isomorphism types. Summarizing, the odd dimensional types split into one type for $d=1$, two for $d=3$ and five in all higher dimensions.

The possible bases of the bipyramid are (up to lattice equivalence) all precisely the $d{-}1$-dimensional, simplicial, terminal, and reflexive $d$-polytopes with $3d-4=3(d-1)-1$ vertices from Theorem 6; all of these are smooth Fano. We do believe that the list of the classifications obtained so far follows a pattern.

Conjecture 9

Let $P$ be a $d$-dimensional smooth Fano polytope with $n$ vertices such that $n\ge 3d-k$ for $k\le \tfrac{d}{3}$. If $d+k$ is even then $P$ is lattice equivalent to $Q\oplus P_6^{\oplus \big (\frac{d-3k}{2}\big )}$ where $Q$ is a $3k$-dimensional smooth Fano polytope with $n-3d+9k\ge 8k$ vertices. If $d+k$ is odd then $P$ is lattice equivalent to $Q\oplus P_6^{\oplus \big (\frac{d-3k-1}{2}\big )}$ where $Q$ is a $(3k{+}1)$-dimensional smooth Fano polytope with $n-3d+9k-3\ge 8k-3$ vertices.

This conjecture is the best possible in the following sense: The $k$-fold direct sum of skew bipyramids over $P_6$ yields a smooth Fano polytope of dimension $d=3k$ with $8k=3d-k$ vertices which doesn’t admit to split off a single copy of $P_6$ as a direct summand. However, it does contain $P_6^{\oplus k}$ as a subpolytope of dimension $2k=\tfrac{2}{3}d$.

If the conjecture above holds the full classification of the smooth Fano polytopes of dimension at most nine [15] would automatically yield a complete description of all $d$-dimensional smooth Fano polytopes with at least $3d-3$ vertices.

3 Toric Varieties

Regarding a lattice point $a\in {\mathbb {Z}}^d$ as the exponent vector of the monomial $z^a=z_1^{a_1}z_2^{a_2}\ldots z_d^{a_d}$ in the Laurent polynomial ring ${\mathbb {C}}[z_1^{\pm 1},z_2^{\pm 1},\ldots ,z_d^{\pm 1}]$ provides an isomorphism from the additive group of ${\mathbb {Z}}^d$ to the multiplicative group of Laurent monomials. This way the maximal spectrum $X_\sigma$ of a lattice cone $\sigma$ becomes an affine toric variety. If $\Sigma$ is a fan of lattice cones, gluing the duals of the cones along common faces yields a (projective) toric variety $X_\Sigma$. This complex algebraic variety admits a natural action of the embedded dense torus corresponding to (the dual of) the trivial cone $\{\mathbf 0\}$ which is contained in each cone of $\Sigma$. If $P\in {\mathbb {R}}^d$ is a lattice polytope containing the origin, then the face fan

$$\begin{aligned} \Sigma (P) = \left\{ {{\mathrm{pos}}}(F)\,\right. \left| \,F \text { face of } P\right\} \end{aligned}$$

is such a fan of lattice cones. We denote the associated toric variety by $X_P=X_{\Sigma (P)}$. The face fan of a polytope is isomorphic to the normal fan of its polar. Two lattice polytopes $P$ and $Q$ are lattice equivalent if and only if $X_P$ and $X_Q$ are isomorphic as toric varieties.

Let $P$ be a full-dimensional lattice polytope containing the origin as an interior point. Then the toric variety $X_P$ is smooth if and only if $P$ is smooth in the sense of the definition given above, that is, the vertices of each facet of $P$ are required to form a lattice basis. A smooth compact projective toric variety $X_P$ is a toric Fano variety if its anticanonical divisor is very ample. This holds if and only if $P$ is a smooth Fano polytope; see Ewald [10, §VII.8.5].

We now describe the toric varieties arising from the polytopes listed in our Theorem 7. For the list of two-dimensional toric Fano varieties we use the same notation as in Fig. 1; see Ewald [10, §VII.8.7]. The toric variety $X_{P_3}$ is the complex projective plane ${\mathbb {P}}_2$. The toric variety $X_{P_{4a}}$ is isomorphic to a direct product ${\mathbb {P}}_1\times {\mathbb {P}}_1$ of lines, and $X_{P_{4b}}$ is the smooth Hirzebruch surface ${\mathcal {H}}_1$. The toric variety $X_{P_5}$ is a blow-up of ${\mathbb {P}}_2$ at two points or, equivalently, a blow-up of ${\mathbb {P}}_1\times {\mathbb {P}}_1$ at one torus invariant point. The toric varieties associated with the del Pezzo polytopes $\mathrm{DP }(d)$ are called del Pezzo varieties; see Casagrande [6, §3] for a detailed description. As a special case the toric variety $X_{P_6}$ is a del Pezzo surface or, equivalently, a blow-up of ${\mathbb {P}}_2$ at three non-collinear torus invariant points. Notice that in algebraic geometry del Pezzo varieties is an ambiguous term.

Two polytope constructions play a role in our classification, direct sums and (skew) bipyramids. We want to translate them into the language of toric varieties. Let $P\subset {\mathbb {R}}^d$ and $Q\subset {\mathbb {R}}^e$ both be full-dimensional lattice polytopes containing the origin. Then the toric variety $X_{P\oplus Q}$ is isomorphic to the direct product $X_P\times X_Q$. In particular, for $P=[-1,1]$ we have that the toric variety

$$\begin{aligned} X_{[-1,1]\oplus Q} = {\mathbb {P}}_1 \times X_Q \end{aligned}$$

over the regular bipyramid over $Q$ is a direct product with the projective line ${\mathbb {P}}_1\cong X_{[-1,1]}$. More generally, the toric variety of a skew bipyramid over $Q$ is a toric fiber bundle with base space ${\mathbb {P}}_1$ and generic fiber $X_Q$; see Ewald [10, §VI.6.7]. An example is the smooth Hirzebruch surface ${\mathcal {H}}_1\cong X_{P_{4b}}$, which is a (projective) line bundle over ${\mathbb {P}}_1$.

In order to translate Theorem 7 to toric varieties we need a few more definitions. For the sake of brevity we explain these in polytopal terms and refer to Ewald’s monograph [10] for the details. A toric variety $X_P$ associated with a canonical lattice $d$-polytope $P$ is ${\mathbb {Q}}$ -factorial (or quasi-smooth) if $P$ is simplicial; see [10, §VI.3.9]. In this case the Picard number equals $n-d$ where $n$ is the number of vertices of $P$; see [10, §VII.2.17]. We call a toric variety, $X$, a 2-stage fiber bundle with a pair $(Y,Z)$ of base spaces if $X$ is a fiber bundle with base space $Z$ such that the generic fiber itself is a fiber bundle with base space $Y$. We say that $Y$ is the base space of the first stage while $Z$ is the base space of the second stage. That is, in order to construct $X$ one starts out with the generic fiber of the first stage, then forms a fiber product with the first base space $Y$, afterwards takes the resulting space as the new generic fiber to finally form $X$ as a fiber product with the second base space $Z$.

Corollary 10

Let $X$ be a $d$-dimensional terminal ${\mathbb {Q}}$-factorial Gorenstein toric Fano variety with Picard number $2d-2$. We assume $d\ge 4$.

If $d$ is even, then $X$ is isomorphic to

• (i) a $2$-stage toric fiber bundle such that the base spaces of both stages are projective lines and the generic fiber of the first stage is the direct product of $\frac{d-2}{2}$ copies of the del Pezzo surface $X_{P_6}$, or

• (ii) the direct product of two copies of $X_{P_5}$ and $\frac{d}{2}-2$ copies of $X_{P_6}$ or

• (iii) the direct product of the del Pezzo fourfold $X_{\mathrm{DP }(4)}$ and $\frac{d}{2}-2$ copies of $X_{P_6}$. If $d$ is odd then $X$ is isomorphic to

• (iv) a toric fiber bundle over a projective line with generic fiber isomorphic to the direct product of $X_{P_5}$ and $\frac{d-3}{2}$ copies of $X_{P_6}$.

All fiber bundles in the preceding result may or may not be trivial.

Remark 11

As for the polytopes in Theorem 7 we can refine the above cases into equivalence classes up to toric isomorphisms. By Remark 8 there is one type for $d=1$, two types for $d=2, 3$, ten for $d=4$, five for any odd dimension $d\ge 5$ and eleven for even dimensions $d\ge 6$. In dimensions up to $4$ this has been classified previously [1, 3].

4 Terminal, Simplicial, and Reflexive Polytopes

4.1 Special Facets and $\eta$-Vectors

Let $P\subset {\mathbb {R}}^d$ be a reflexive lattice $d$-polytope with vertex set $\mathrm{Vert }(P)$. In particular, the origin $\mathbf 0$ is an interior point. We let

$$\begin{aligned} v_P \,\, {:}{=} \sum _{v\in \mathrm{Vert }(P)} v \end{aligned}$$

be the vertex sum of $P$. As $P$ is a lattice polytope, the vertex sum is a lattice point. Now, a facet $F$ of $P$ is called special if the cone ${{\mathrm{pos}}}F$ in the fan contains the vertex sum $v_P$. Since the fan $\Sigma (P)$ generated by the facet cones is complete, a special facet always exists. However, it is not necessarily unique. For instance, if $P$ is centrally symmetric, we have $v_P=\mathbf 0$, and each facet is special.

Since $P$ is reflexive, for each facet $F$ of $P$ there is a unique (outer) facet normal vector $u_F$ in the dual lattice $M\cong {\mathbb {Z}}^d$ and $\alpha \in {\mathbb {Z}}$ which satisfies the following:

• (i) $u_F$ is primitive, that is, there is no lattice point strictly between 0 and $u_F$,

• (ii) the affine hyperplane spanned by $F$ is the set $\{x\in {\mathbb {R}}^d\,|\,\langle u_F,x\rangle =1\}$,

• (iii) and $\langle u_F,x\rangle \le 1$ for all points $x\in P$.

The vector $u_F$ is called the standard outer normal vector of $F$. We define

$$\begin{aligned}&H(F,k)\,\, {:}{=} \{ x\in {\mathbb {R}}^d | \langle u_F,x\rangle =k \},\\&V(F,k)\,\, {:}{=}\, H(F,k) \cap \mathrm{Vert }(P) \end{aligned}$$

and

$$\begin{aligned} \eta ^F_k\,\, {:}{=} \, |V(F,k)| \end{aligned}$$

for any integer $k\le 1$. We have

$$\begin{aligned} \mathrm{Vert }(P) \,{:}{=}\, \bigcup _{k\le 1} V(F,k) \, \subset \ \bigcup _{k\le 1} H(F,k) \end{aligned}$$

and thus $\eta ^F_{1}+\eta ^F_{0}+\eta ^F_{-1}+\cdots =|\mathrm{Vert }(P)|$ is the number of vertices of $P$. If a vertex $v$ is contained in $V(F,k)$ we call the number $k$ the level of $v$ with respect to $F$. The sequence of numbers $\eta ^F=(\eta ^F_1,\eta ^F_0,\eta ^F_{-1},\ldots )$ is the $\eta$ -vector of $P$ with respect to $F$. If the choice of the facet is obvious from the context we omit the upper index $F$ in our notation. Notice that the following lemma does not need terminality.

Lemma 12

Let $P$ be a simplicial and reflexive polytope. The level of $v_P$ is the same for any special facet of $F$.

Proof

This is obvious if $v_P=0$. So suppose otherwise. Let $F_1, F_2, \ldots , F_m$ be the special facets of $P$. By assumption, $v_P$ is contained in the cone $C\,{:}{=}{{\mathrm{pos}}}(F_1\cap F_2\cap \cdots \cap F_m)$. If $v_1, v_2, \ldots , v_\ell$ are the vertices in the common intersection of the special facets, then there are coefficients $\lambda _1, \lambda _2, \ldots , \lambda _\ell \ge 0$ such that

$$\begin{aligned} v_P\ = \ \sum _{i=0}^{\ell }\lambda _i v_i. \end{aligned}$$

Since $P$ is simplicial the coefficients $\lambda _i$ are unique. We define $k\, {:}{=}\, \sum _{i=1}^{\ell }\lambda _i$. Note that $\langle u_{F_j}, v_i\rangle = 1$ for all $1\le j\le m$ and $1\le i\le \ell$, as $P$ is reflexive. Hence,

$$\begin{aligned} \langle u_{F_j}, v_P \rangle = \Big \langle u_{F_j}, \sum _{i=1}^{\ell }\lambda _i v_i \Big \rangle \ =\ \sum _{i=1}^{\ell }\lambda _i \langle u_{F_j}, v_i \rangle = \sum _{i=1}^{\ell }\lambda _i\ =\ k. \end{aligned}$$

This means $v_P$ is on level $k$ for all special facets. $\square$

Thus, the common level of $v_P$ for all special facets is an invariant of $P$, which we call the eccentricity ${{\mathrm{ecc}}}(P)$.

Example 13

Consider the $3$-dimensional lattice polytope $A$ (shown in Fig. 3) with the seven vertices

$$\begin{aligned}&\qquad \qquad e_1,\ e_2,\ e_3 ;\\&e_1-e_2,\ e_2-e_1,\ e_1-e_3;\\&\qquad \qquad \qquad -e_1 . \end{aligned}$$

The vertex sum equals $e_1+e_2$, and the two facets

$$\begin{aligned} F \,{:}{=} {{\mathrm{conv}}}\{e_1,\,e_2,e_3\} \quad \text {and} \quad G \, {:}{=} \, {{\mathrm{conv}}}\{e_1, e_2, e_1-e_3\} \end{aligned}$$

are special, the remaining eight facets are not. We have $u_F=\mathbf 1$ and $u_G=e_1+e_2=\mathbf 1-e_3$. The vertices are listed by level with respect to the facet $F$. The $\eta$-vectors

$$\begin{aligned} \eta ^F = (3,3,1) \, = \eta ^G \end{aligned}$$

coincide. The polytope $A$ is a skew bipyramid with apices $e_3$ and $e_1-e_3$ over the pentagon $P_5={{\mathrm{conv}}}\{\pm e_1,e_2,\pm (e_1-e_2)\}$. The latter is smooth Fano and so is $A$ due to Lemma 3. The polytope $A$ is the polytope F.3D.0002.poly in the file fano-v3d.tgz provided in [15]. The polytope can also be found in the new polymake database, polydb, with ID F.3D.0002; see www.polymake.org for more details.

Fig. 3

The polytope $A$ from Example 13. Its two special facets are the ones containing $e_1$ and $e_2$

The following example shows that the $\eta$-vector does depend on the choice of the special facet.

Example 14

We also consider the smooth Fano $4$-polytope $B$ which is the convex hull of the ten vertices

$$\begin{aligned}&e_1 ,\ e_2 ,\ e_3 ,\ e_4 ;\\&e_1-e_2 ,\ e_2-e_1 ;\\&-e_1 ,\ -e_2 ;\\&e_1 - e_2 - e_3 , e_2-e_1-e_4 . \end{aligned}$$

Here the vertex sum vanishes, and so all $24$ facets are special. Two examples are

$$\begin{aligned} F \, {:}{=} {{\mathrm{conv}}}\{e_1,\, e_2,\, e_3,\, e_4\} \quad \text {and} \quad H \,{:}{=} {{\mathrm{conv}}}\{e_2,\, e_3,\, e_4,\, e_2-e_1\} . \end{aligned}$$

Again the vertices are listed by level with respect to the facet $F$. We have $u_F=\mathbf 1$ and $u_H=-e_2-e_3-e_4=\mathbf 1-e_1$. This yields

$$\begin{aligned} \eta ^F = (4,2,4) \quad \text {and} \quad \eta ^H = (4,3,2,1) . \end{aligned}$$

The unique vertex at level $-2$ with respect to $H$ is $e_1-e_2-e_3$. This polytope is F.4D.0066.poly in the file fano-v4d.tgz in [15]. The polytope can also be found in the new polymake database, polydb, with ID F.4D.0066; see www.polymake.org for more details.

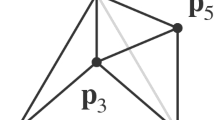
Throughout the paper we will return to these two examples. Let $F$ be a facet of a simplicial $d$-dimensional polytope with $F = {{\mathrm{conv}}}\{ v_1, \ldots , v_d \}$. To every $v_i \in F$ there is a unique ridge $R={{\mathrm{conv}}}(\mathrm{Vert }(F) \setminus \{ v_i \})$ and a unique facet $G \ne F$ such that $G\cap F = R$. We will call this facet the neighboring facet of $F$ with respect to $v_i$, and it will be denoted by $\mathrm{N }(F,v_i)$. There also is a unique vertex $v \in \mathrm{Vert }(P)$ such that $\mathrm{N }(F,v_i) = {{\mathrm{conv}}}( R \cup \{ v \})$. This vertex will be called opposite vertex of $v_i$ with respect to $F$ and will be denoted by ${{\mathrm{opp}}}(F,v_i)$. To make things a little bit clearer see Fig. 4.

Fig. 4

Neighboring facets and opposite vertices

Example 15

Let $B$ be the 4-polytope from Example 14. The two facets $F$ and $H$ are adjacent with $H=\mathrm{N }(F,e_1)$ and ${{\mathrm{opp}}}(F,e_1)=e_2-e_1$.

4.2 Coordinates and Lattice Bases

Throughout let $P\subset {\mathbb {R}}^d$ be a simplicial and reflexive $d$-polytope for $d\ge 2$. Let $v$ be a vertex of $P$ and let $F$ be a facet containing $v$. The vertices of $F$ form a basis of ${\mathbb {R}}^n$, and hence there is a unique vector $u_{F,v}$, the vertex normal of $v$ with respect to $F$, satisfying

$$\begin{aligned} \langle u_{F,v}, v\rangle = 1, \quad \text {and} \quad \langle u_{F,v},w\rangle = 0 \text { for all } w\in \mathrm{Vert }(F)\setminus \{v\}. \end{aligned}$$

That is to say, the set $\{u_{F,v}\,|\,v\in \mathrm{Vert }(F)\}$ is the basis dual to $\mathrm{Vert }(F)$. For the reader’s benefit we explicitly list a few known facts which will be useful in our proofs below. Notice that here we do not assume that the vertices of $F$ form a lattice basis.

Lemma 16

(Øbro [20, Lem. 1 and 2]) Let $F$ be a facet of $P, v$ a vertex of $F$, and $G\,{:}{=}\,\mathrm{N }(F,v)$. If $x\in P$ then

$$\begin{aligned} \langle u_G,x \rangle = \langle u_F, x\rangle + \left( \langle u_G,v \rangle -1 \right) \langle u_{F,v} ,x \rangle . \end{aligned}$$

Moreover $\langle u_{F}, x \rangle -1 \le \langle u_{F,v}, x \rangle$. In case of equality we have $x = {{\mathrm{opp}}}(F,v)$.

Example 17

Let $P$ be a simplicial, terminal, and reflexive $d$-polytope such that the standard basis vectors span a facet $F={{\mathrm{conv}}}\{ e_1, e_2,\ldots , e_d \}$. Further, let $x \in V(F,-1)$ and $z={{\mathrm{opp}}}(F,e_i)$ for some $i\in [d]$, with $x\ne z$. The previous lemma shows that

$$\begin{aligned} x_i = \langle u_{F,e_i}, x \rangle = \frac{\langle u_{\mathrm{N }(F,e_i)}, x \rangle +1}{(\langle \mathbf 1, z \rangle -1 ).} \end{aligned}$$

Moreover, this gives

$$\begin{aligned} \langle u_{\mathrm{N }(F,e_i)}, x \rangle \, < \, 1 -2 \langle \mathbf 1,z \rangle \, . \end{aligned}$$

We say that two lattice points $v,w\in \partial P\cap {\mathbb {Z}}^n$ are distant if they are not contained in a common face. We have the following facts about distant lattice points.

Lemma 18

(Nill [16, Lem. 4.1] ) Consider two lattice points $v,w$ in the boundary of $P$ such that $v\ne -w$. Then $v+w\in \partial P\cap {\mathbb {Z}}^n$ if and only if $v$ and $w$ are distant.

Example 19

The polytope A of Example 13 has four pairs of distant vertices: $(e_1, e_2-e_1), (e_1,-e_2), (e_2,e_1-e_2)$, and $(e_3,e_1-e_3)$.

Proposition 20

(Nill [16, Lem. 5.5]) Let $F$ be a facet of $P$, and let $x\in {\mathbb {Z}}^d$ be any lattice point in $\partial P\cap H(F,0)$. Then

• (i) the point $x$ is contained in a facet adjacent to $F$,

• (ii) for each vertex $v$ of $F$ we have $x\ne {{\mathrm{opp}}}(F,v)$ if and only if $\langle u_{F,v}, x \rangle \ge 0$,

• (iii) if there is a vertex $v$ of $F$ such that $x={{\mathrm{opp}}}(F,v)$ and $x\ne {{\mathrm{opp}}}(F,w)$ for any other vertex $w\ne v$ of $F$, then $v$ and $x$ are distant.

This technical but powerful result has the following consequence. Remember that $P$ is a simplicial polytope.

Corollary 21

Let $F\subseteq P$ be a facet and $x\in V(F,0)$. Then $x$ is opposite to some vertex of $F$.

For the sake of brevity we call a vertex $v$ of the facet $F$ good if ${{\mathrm{opp}}}(F,v)$ is contained in $V(F,0)$ and the equality $\langle u_{F,v},{{\mathrm{opp}}}(F,v) \rangle =-1$ holds.

Example 22

All four vertices of the facet $F$ of the polytope $B$ from Example 14 are good: for instance, $u_{F,e_1}=e_1$ and ${{\mathrm{opp}}}(F,e_1)=e_2-e_1$ such that $\langle u_{F,e_1},{{\mathrm{opp}}}(F,e_1) \rangle =-1$.

Lemma 23

(Nill [16, Lem. 5.5]) If the facet $F$ of $P$ contains at least $d-1$ pairwise distinct good vertices, then the vertices of $F$ form a lattice basis.

A recurring theme in our paper is that the simplicial, terminal, and reflexive polytopes within the class we consider turn out to be smooth. In this the preceding observation is a key ingredient.

4.3 Characterizing Vertices in $V(F,0)$

Throughout this section we assume that $P\subset {\mathbb {R}}^d$ is a $d$-dimensional simplicial, terminal, and reflexive polytope with a fixed facet $F$. The purpose of this section is to investigate the situation where the hyperplane $H(F,0)$ contains “many” vertices. In particular, if there are at least $d-1$ good vertices in $V(F,0)$ then we can apply Lemma 23. In this case, up to a unimodular transformation, we may assume that the standard basis vectors of ${\mathbb {R}}^d$ coincide with the vertices of $F$.

It will be convenient to phrase some of the subsequent results on the vertices in $V(F,0)$ in terms of the function

$$\begin{aligned} \phi : \mathrm{Vert }(F) \rightarrow \mathrm{Vert }(F)\cup \{\mathbf{0}\} \,,\; v\mapsto {\left\{ \begin{array}{ll} w &{} \text {if } w={{\mathrm{opp}}}(F,v)+v\in \mathrm{Vert }(F) \\ \mathbf{0} &{} \text {otherwise }. \end{array}\right. } \end{aligned}$$

(4)

Occasionally, we additionally let $\phi (\mathbf 0)=\mathbf 0$ in which case $\mathbf 0$ becomes the only fixed point. Clearly, like the $\eta$-vector also the function $\phi$ depends on the choice of the facet $F$. If we want to express this dependence we write $\phi ^F$ instead. Vertices that satisfy $\phi (v)\ne \mathbf 0$ are necessarily good, since then ${{\mathrm{opp}}}(F,v)=\phi (v)-v$ and

$$\begin{aligned} \langle u_{F,v},{{\mathrm{opp}}}(F,v)\rangle = \langle u_{F,v},\phi (v)\rangle -\langle u_{F,v},v\rangle = 0-1 = -1 \,. \end{aligned}$$

However the converse is not true. It is possible that $v$ is a good vertex and satisfies $\phi (v) = 0$. It means that the opposite vertex of $v$ is not of the form $\phi (v) - v$ but it could still be in $V(F,0)$.

Example 24

The function $\phi ^F$ for the facet $F$ of the $3$-polytope $A$ from Example 13 reads as follows: $\phi ^F(e_1)=e_2$ and $\phi ^F(e_2)=\phi ^F(e_3)=e_1$. This implies that $e_1, e_2$ and $e_3$ are good, but as said above not every good vertex has $\phi (v)\ne 0$. To see this look at the del Pezzo polytope $\mathrm{DP }(4)$ in dimension $4$. The facet $H={{\mathrm{conv}}}\{ e_1,e_2,-e_3,-e_4 \}$ has outer facet normal vector $u_H = e_1+e_2-e_3-e_4$. In this situation all vertices of $H$ are good as ${{\mathrm{opp}}}(H,e_1) = {{\mathrm{opp}}}(H,e_2) = -\mathbf 1$ and ${{\mathrm{opp}}}(H,-e_3) = {{\mathrm{opp}}}(H,-e_4) = \mathbf 1$ and $\pm \mathbf 1 \in V(H,0)$. But we get $\phi ^H(v)=0$ for every vertex $v$ of $H$ as $\pm \mathbf 1$ cannot be expressed as a sum of only two vertices in $H$.

Notice that $\phi (v)\ne \mathbf 0$ implies that the vertex ${{\mathrm{opp}}}(F,v)=\phi (v)-v$ is contained in the set $V(F,0)$. The following partial converse slightly strengthens [20, Lem. 6], but the proof is essentially the same.

Lemma 25

Let $v$ be a vertex of $F$ such that ${{\mathrm{opp}}}(F,v) \in V(F,0)$. If for every vertex $w\in \mathrm{Vert }(F)$ other than $v$ we have that ${{\mathrm{opp}}}(F,w) \ne {{\mathrm{opp}}}(F,v)$ then $\phi (v)\ne \mathbf 0$.

Proof

The vertices of $F$ form a basis of ${\mathbb {R}}^d$, albeit not necessarily a lattice basis. Using Proposition 20(ii) and our assumption we can write

$$\begin{aligned} v' \, {:}{=} {{\mathrm{opp}}}(F,v) = -\alpha v + \sum _{w \in W} \beta _w w \end{aligned}$$

for some set $W\subset \mathrm{Vert }(F)\setminus \{v\}$ and $\alpha >0$ as well as $\beta _w > 0$ for all $w\in I$. Since $v' \in V(F,0)$ we have $\sum _{w\in W}\beta _w = \alpha$, and the set $W$ is not empty. If there were a facet $G$ containing both $v$ and $v'$ then

$$\begin{aligned} 1+\alpha = \langle u_G, v' + \alpha v \rangle = \Big \langle u_G, \sum _{w\in W} \beta _w w \Big \rangle \ \le \ \sum _{w\in W}\beta _w = \alpha , \end{aligned}$$

which is a contradiction. So $v$ and $v'$ are distant, and by Lemma 18 $v+v'\in \partial P$. The polytope $P$ is terminal by assumption, so $v+v'$ is a vertex. As $v'\in V(F,0)$ we have $v+v' \in V(F,1)$. So there must be a vertex $w$ of $F$ with $w = v+v'$. Hence, $v'=w-v$, or, equivalently, $\phi (v) = w$. $\square$

The following is now a direct consequence of Lemmas 25, 23 and Corollary 21.

Lemma 26

(Øbro [20, Lem. 6]) If $\eta _0=d$ then $V(F,0) = \left\{ \phi (v)-v \,\right. \left| \, v\in \mathrm{Vert }(F) \right\}$. In particular, the vertices of $F$ form a lattice basis.

We can investigate a situation similar to Lemma 25 more closely. It indicates why simplicial, terminal, and reflexive polytopes with many vertices are prone to be smooth.

Proposition 27

Let $P$ be a $d$-dimensional simplicial, terminal, and reflexive polytope such that $F$ is a special facet of $P$ with $\eta ^F_0 \ge d-1$. Then the vertices of $F$ form a lattice basis. Further, for at least $d-2$ vertices of $F$ we have $\phi (v)\ne \mathbf 0$.

Proof

The case $\eta ^F_0=d$ is handled in Lemma 26, so we assume that $\eta _0=d-1$. Since every element in $V(F,0)$ must be opposite to some vertex of $F$ we see that the conditions of Lemma 25 are satisfied for at least $d-2$ vertices of $F$. So we are left with two cases:

• there exists exactly one vertex $v$ of $F$ with ${{\mathrm{opp}}}(F,v) \not \in V(F,0)$, or

• there are exactly two vertices $v$ and $w$ of $F$ with ${{\mathrm{opp}}}(F,v)={{\mathrm{opp}}}(F,w) \in V(F,0)$.

In the first case we have $d-1$ good vertices. This makes the vertices of $F$ a lattice basis according to Lemma 23.

In the second case we look at the vertex $z\, {:}{=} {{\mathrm{opp}}}(F,v)={{\mathrm{opp}}}(F,w) \in V(F,0)$. We express $z=-z_vv-z_ww+\sum _{x\in \mathrm{Vert }(F)\setminus \{v,w\}} z_x x$ in the coordinates given by the basis $\mathrm{Vert }(F)$ of ${\mathbb {R}}^d$. We have $z_v=-\langle u_{F,v}, z \rangle > 0$ and $z_w=-\langle u_{F,w}, z \rangle > 0$. The remaining $d-2$ vertices of $F$ are good. Hence Proposition 20(ii) forces $z_x=\langle u_{F,x}, z \rangle \ge 0$ for all $x\ne v,w$.

Suppose that $z_x$ is not integral for some $x\in \mathrm{Vert }(F)\setminus \{v,w\}$, and let $G\,{:}{=}\,\mathrm{N }(F,x)$. Note that $\langle u_G, x \rangle =\langle u_G, \phi (x) \rangle - \langle u_G, \phi (x) -x \rangle = 1-1 = 0$, since $\phi (x)$ and $\phi (x)-x$ are vertices of $G$. By Lemma 16

$$\begin{aligned} \langle u_G,z \rangle \, = \, \langle u_F, z\rangle + \left( \langle u_G,x \rangle -1 \right) z_x \, = \, - z_x, \end{aligned}$$

so $\langle u_G,z \rangle$ would not be integral, a contradiction. Hence

$$\begin{aligned} z_v + z_w \, = \, \sum _{y\in \mathrm{Vert }(F) \setminus \{ v,w \}} z_y \end{aligned}$$

is an integer. The second part of Lemma 16 also implies that $z_v, z_w \le 1$. Hence, $z_v+z_w\in \{1,2\}$. If $z_v+z_w=2$, then $z_v = z_w = 1$, and the vertices $v$ and $w$ are good. Hence the vertices of $F$ form a lattice basis. If $z_v + z_w = 1$, then $z_vv+z_ww$ is a proper convex combination of $v$ and $w$. We can write this as

$$\begin{aligned} z_vv+z_ww = -z\ +\ \sum _{y\in \mathrm{Vert }(F) \setminus \{ v,w \}} z_y y. \end{aligned}$$

Since both summands on the right hand side are integral this implies that $z_v v + z_w w\in {\mathbb {Z}}^d$. This contradicts the terminality of $P$. $\square$

The next result helps to identify facets.

Lemma 28

Let $v$ and $w$ be distinct vertices of $F$ such that $\phi (v)\ne \mathbf 0$ and $\phi (w)\not \in \{\mathbf 0,v\}$. Then the $(d{-}1)$-simplex

$$\begin{aligned} {{\mathrm{conv}}}( (\mathrm{Vert }(F)\setminus \{v,w\}) \cup \{ \phi (v)-v,\phi (w)-w \} ) \end{aligned}$$

is a facet of $P$.

Proof

As $\phi (v)\ne \mathbf 0$ we know that $v'\,{:}{=}\,\phi (v)-v={{\mathrm{opp}}}(F,v)$, and this means that ${{\mathrm{conv}}}((\mathrm{Vert }(F)\setminus \{v\})\cup \{v'\})=\mathrm{N }(F,v)$ is a facet. For $w' \,{:}{=}\phi (w)-w={{\mathrm{opp}}}(F,w)$ the assumption $\phi (w)\not \in \{\mathbf 0,v\}$ yields

$$\begin{aligned} \langle u_{\mathrm{N }(F,v)},w'\rangle = \langle u_{\mathrm{N }(F,v)},\phi (w)\rangle - \langle u_{\mathrm{N }(F,v)},w \rangle \ = \ 1-1 \ = \ 0\, \end{aligned}$$

as both $\phi (w)$ and $w$ are vertices of $\mathrm{N }(F,v)$, and because $P$ is reflexive the scalar product of those vertices with the facet normal vector evaluates to $1$. Furthermore we get

$$\begin{aligned} \langle u_{\mathrm{N }(F,v),w},w'\rangle = \langle u_{\mathrm{N }(F,v),w},\phi (w)\rangle - \langle u_{\mathrm{N }(F,v),w},w \rangle \ = \ 0-1 \ = \ -1\,. \end{aligned}$$

Now Lemma 16 says that ${{\mathrm{opp}}}(\mathrm{N }(F,v),w)=w'$, and hence, $\mathrm{Vert }(\mathrm{N }(F,v))\setminus \{ w \}) \cup \{ w' \}$ is the set of vertices of the facet $\mathrm{N }(\mathrm{N }(F,v),w)$ of $P$. This is the claim. $\square$

Next we want to extract more information about the function $\phi$ by taking into account vertices at level $-1$ and below. If $d$ is even and $P$ has at least $3d-1$ vertices with $\eta _0=d$ then it follows from Theorem 6 that $\phi$ is an involutory permutation of the vertices of $F$; that is, we have $\phi (\phi (v))=v$ for all $v\in \mathrm{Vert }(F)$. This can be generalized as follows. Recall that $\phi (v)=\mathbf 0$ means that the vertex ${{\mathrm{opp}}}(F,v)$ is not of the form $w-v$ for any vertex $w\in \mathrm{Vert }(F)$.

Lemma 29

Let $v$ be a vertex of $F$ satisfying $\phi (v)\ne \mathbf 0$. If $-v$ is a vertex of $P$ then $\phi (\phi (v)) \in \{ \mathbf 0,v \}$.

Proof

Aiming at a contradiction suppose that $\phi (\phi (v)) =x$ for some vertex $x\ne v$ of $F$. Letting $w=\phi (v)$ the three vertices $v,w,x$ are pairwise distinct. Now Lemma 28 gives us that

$$\begin{aligned} G \, = \, {{\mathrm{conv}}}( (\mathrm{Vert }(F)\setminus \{v,w\}) \, \cup \{ w-v,x-w \} ) \end{aligned}$$

(5)

is a facet. In particular, $G$ contains the three vertices $w-v, x-w$, and $x$. Hence the equation

$$\begin{aligned} 1 \, = \, 1+1-1 \, = \, \langle u_G, w-v \rangle + \langle u_G, x-w \rangle - \langle u_G, x \rangle \, = \, \langle u_G, -v \rangle \end{aligned}$$

shows that $-v$ is contained in $G$, too. However $-v$ is none of the $d$ vertices listed in (5). This is the contradiction desired, as each face of $P$ is a simplex. $\square$

Example 30

The polytope $A$ of Example 13 contains the vertex $-e_1$, which implies that $\phi (\phi (e_1))=\phi (e_2)=e_1$.

The following lemma says how good vertices at level zero restrict the vertices at level $-1$.

Lemma 31

(Øbro [20, Lem. 5]) Let $v$ and $w\ne v$ be good vertices of $F$ with ${{\mathrm{opp}}}(F,v) \ne {{\mathrm{opp}}}(F,w)$. Then there is no vertex $x\in V(F,-1)$ such that $\langle u_{F,v}, x\rangle = \langle u_{F,w}, x\rangle = -1$.

The subsequent lemma is an important clue in the proof of Øbro ’s classification Theorem 6.

Lemma 32

(Øbro [20, Lem. 7]) If $\eta _0=d$ then all vertices in $V(F,-1)$ are of the form $-v$ for some vertex $v\in \mathrm{Vert }(F)$.

We summarize all considerations in the following Proposition. To simplify the notation we let ${{\mathrm{opp}}}(F)\,{:}{=}\{{{\mathrm{opp}}}(F,v)\,|\,v\in \mathrm{Vert }(F)\}$ for any facet $F$ of the polytope $P$. Further, we we abbreviate “pairwise distinct” as “p.d.”.

Proposition 33

Let $P$ be a $d$-dimensional simplicial, terminal, and reflexive polytope such that $F$ is a special facet.

• (i) If $\eta ^F_0=d$, then, up to lattice equivalence, $F={{\mathrm{conv}}}\{e_1,e_2, \ldots , e_d\}$, and

  $$\begin{aligned} V(F,0)&= \{\phi (e_1)-e_1, \phi (e_2)-e_2, \ldots , \phi (e_d)-e_d\},\\ V(F,-1)&\subseteq \{-e_1, -e_2, \ldots , -e_d\}. \end{aligned}$$

• (ii) If $\eta ^F_0=d-1$ and ${{\mathrm{opp}}}(F) = V(F,0)$, then, up to lattice equivalence, $F={{\mathrm{conv}}}\{e_1, e_2, \ldots , e_d\}$, and

  $$\begin{aligned} V(F,0)&= \{-e_1-e_2+e_a+e_b, \phi (e_3)-e_3, \ldots ,\, \phi (e_d)-e_d\},\\ V(F,-1)&\subseteq \{-e_1, -e_2, \ldots , -e_d\} \;\cup \; \left\{ -e_1-e_2 + e_s\,\right. \left| \,s\in [d]\right\} \end{aligned}$$

  for $a, b \in [d] \setminus \{ 1,2 \}$ not necessarily distinct.

• (iii) If $\eta ^F_0=d-1$ and ${{\mathrm{opp}}}(F)\ne V(F,0)$, then, up to lattice equivalence, $F={{\mathrm{conv}}}\{e_1,e_2, \ldots , e_d\}$, and

  $$\begin{aligned} V(F,0)&= \{\phi (e_2)-e_2, \phi (e_3)-e_3, \ldots , \phi (e_d)-e_d\},\\ V(F,-1)&\subseteq \{-e_1, -e_2, \ldots , -e_d\} \;\cup \; \left\{ -2e_1-e_r +e_s+e_t\,\right. \left| \,r,s,t \in [d] \text { p.d.},\, r\ne 1\right\} . \end{aligned}$$

Proof

Assume first that $\eta ^F_0=d$. Then Lemma 26 implies that the vertices of $F$ form a lattice basis, so up to a lattice transformation we can assume that $F={{\mathrm{conv}}}\{e_1, e_2,\ldots , e_d\}$. The same lemma gives $V(F,0) = \{\phi (e_1)-e_1, \ldots , \phi (e_d)-e_d\}$. By Lemma 32 now $V(F,-1)\subseteq \{-e_1, -e_2, \ldots , -e_d\}$. This proves (i).

From now on we assume that $\eta ^F_0=d-1$. We look first at the case ${{\mathrm{opp}}}(F) = V(F,0)$. By Lemma 27 we know that the vertices of $F$ form a lattice basis, so, up to a lattice transformation, $F={{\mathrm{conv}}}\{e_1,e_2, \ldots , e_d\}$. Further, the function $\phi$ does not vanish for at least $d-2$ vertices in $F$. Since any vertex in $V(F,0)$ is opposite to a vertex of $F$ we know that there is a vertex $x\in V(F,0)$ such that $x\,{:}{=}\,{{\mathrm{opp}}}(F,v)={{\mathrm{opp}}}(F,w)$ for precisely two vertices $v,w$ of $F$. Hence, up to relabeling,

$$\begin{aligned} V(F,0)\ = \ \{\phi (e_3)-e_3, \ldots , \phi (e_d)-e_d\} \;\cup \; \{x\} \end{aligned}$$

Let $x=(x_1, \ldots , x_d)$. By Lemma 16 and Proposition 20(ii) we have $-1\le x_1, x_2<0$ and $x_j\ge 0$ for $j\ge 3$. $x\in {\mathbb {Z}}^d$ implies $x_1=x_2=-1$. And since $\sum _{i=1}^d x_i = 0$ we get that there exist not necessarily distinct indices $a,b \in [d]\setminus \{ 1,2 \}$ with $x=-e_1-e_2 +e_a+e_b$. Now we take a look at an arbitrary $y\in V(F,-1)$. Because of Lemma 31 we know that for two distinct indices $i$ and $j$ it is not possible that $y_i = y_j = -1$ except for $i=1$ and $j=2$ (or vice versa). And since every vertex of $F$ is good Lemma 16 gives us that $y_i \ge -1$ for all $i \in [d]$. Putting this together with the fact that $\sum _{i=1}^d y_i = -1$ leaves us with either $y \in \{ -e_1, -e_2,\ldots ,-e_d \}$ or $y=-e_1-e_2+e_s$ for some $s\in [d]$. This proves (ii).

So finally assume that there is some vertex $v$ in $F$ with ${{\mathrm{opp}}}(F,v) \not \in V(F,0)$. Up to relabeling, $v=e_1$. Then

$$\begin{aligned} V(F,0)\, = \, \{\phi (e_2)-e_2, \ldots , \phi (e_d)-e_d\}. \end{aligned}$$

because of the same argument as above. That is, every vertex in $V(F,0)$ must be opposite to a unique vertex in $F$. Hence, by Lemma 25 we know the entire set $V(F,0)$. Now we look at $y\in V(F,-1)$. Because of Lemma 31 we know that for two distinct indices $i,j \in [d] \setminus \{ 1 \}$ it is not possible that $y_i = y_j = -1$, since all vertices are good except $e_1$. Now let $G = \mathrm{N }(F,e_1)$. Lemma 16 now implies several things. Firstly, we get $y_i \ge -1$ for $i \in [d] \setminus \{ 1 \}$. Together with $\langle u_G, y \rangle \le 1$ we get

$$\begin{aligned} 2 \, \ge \, (\langle u_G, e_1 \rangle -1) x_1 \quad \text {if and only if} \quad x_1 \ \ge \ \frac{2}{\langle u_G,e_1 \rangle -1} . \end{aligned}$$

This implies $x_1 \ge -2$ as $\langle u_G, e_1 \rangle \le 0$ holds. So we are left with $y\in \{ -e_1,-e_2,\ldots , -e_d \}$ or $y=-2e_1-e_r +e_s+e_t$ for some $r,s,t$. Now we want to show that $r,s,t$ are pairwise distinct and $r\ne 1$. We look at all the different cases.

• $r=s=t=1$ would imply $y = -e_1$, a case which is already covered, or

• $s=t$ would imply $y = -2e_1 -e_r + 2e_s$, which is impossible since $P$ is terminal and $-e_1+e_s \in {{\mathrm{conv}}}\{ y, e_r \}$, or

• $r=t$ (the case $r=s$ is similar) would imply $y = -2e_1 + e_s$, which is impossible since $P$ is terminal and $-e_1+e_s \in {{\mathrm{conv}}}\{ y, e_s \}$.

So $r,s,t$ are pairwise distinct. From $x_1 \ge -2$ we get that $r\ne 1$. This proves (iii). $\square$

5 Smooth Fano $d$-polytopes with $3d-2$ Vertices

Throughout this section we assume that $P\subset {\mathbb {R}}^d$ is a $d$-dimensional simplicial, terminal, and reflexive polytope with precisely $3d-2$ vertices. It is a consequence of our main result, which we will prove below, that all such polytopes turn out to be smooth Fano. Let $F$ be a special facet $F$ of $P$, that is, the vertex sum $v_P$ is contained in ${{\mathrm{pos}}}(F)$. We explore the possible shapes of the vector $\eta =\eta ^F$. As in Øbro [20, §5] it is useful to expand the expression $\langle u_F,v_P \rangle$. Since $\eta _1=d$ we obtain

$$\begin{aligned} 0 \, \le \, \langle u_F,v_P \rangle \, = \, d + \sum _{k\le -1} k \cdot \eta _k . \end{aligned}$$

(6)

Hence, in particular, $\eta _{-1}+\eta _{-2}+\cdots \le d$. By Corollary 21 any vertex at level zero with respect to $F$ is opposite to a vertex in $F$, and the total number of vertices is $3d-2$. So we have

$$\begin{aligned} d-2&\le \, \eta _0 \ \le d,\end{aligned}$$

(7)

$$\begin{aligned} d-2&\le \, \sum _{k\le -1} \eta _k \ \le \ d . \end{aligned}$$

(8)

The linear restrictions (6), (7), and (8) now leave us with finitely many choices for $\eta$. The resulting six admissible $\eta$-vectors are displayed in Table 1. In particular, $\eta _k=0$ for $k\le -4$. Notice that in Proposition 43 below we will show that the $\eta$-vector $(d,d,d-3,0,1)$ for $v_P=\mathbf 0$ does not occur. The case distinction by the eccentricity ${{\mathrm{ecc}}}(P)$ of the polytope $P$ is the guiding principle for the proof of our main result.

Table 1 List of possible $\eta$-vectors of simplicial, terminal, and reflexive $d$-polytopes with $3d-2$ vertices, where ${{\mathrm{ecc}}}(P)$ denotes the eccentricity of $P$

Example 34

Let us consider the planar case $d=2$ . The classification in Fig. 1 shows that there are two simplicial, terminal, and reflexive polygons with $3\cdot 2-2=4$ vertices. The vertex sum of $P_{4a}$ is zero, and the vertex sum of $P_{4b}$ equals $e_1$. Taking ${{\mathrm{conv}}}\{e_1,e_2\}$ as a special facet in both cases the $\eta$-vector for that facet of $P_{4a}$ reads $(2,0,2)$, corresponding to the last column of Table 1. For $P_{4b}$ the $\eta$-vector of that facet reads $(2,1,1)$, corresponding to the third column.

Let $P$ be a simplicial, terminal, and reflexive $d$-polytope with $3d-1$ vertices, and let $Q$ be an simplicial, terminal, and reflexive $e$-polytope with $3e-1$ vertices, as in Øbro ’s classification Theorem 6. Then $P\oplus Q$ is a simplicial, terminal, and reflexive polytope of dimension $d+e$ with $3(d+e)-2$ vertices. Clearly, the vertex sum is $v_{P\oplus Q}=v_P+v_Q$. If $F$ is a special facet for $P$ and $G$ is a special facet for $Q$ then the joint convex hull ${{\mathrm{conv}}}(F\cup G)$ in ${\mathbb {R}}^{d+e}$ is a special facet for $P\oplus Q$. A direct computation gives

$$\begin{aligned} \eta ^{{{\mathrm{conv}}}(F\cup G)}_\ell \, = \, \eta ^F_\ell +\eta ^G_\ell \, . \end{aligned}$$

It turns out that the only polytopes in dimension ${\ge } 4$ in our classification which are not of this type are $\mathrm{DP }(4)$ and its direct sums with copies of the del Pezzo hexagon $\mathrm{DP }(2)\cong P_6$.

5.1 Polytopes of Eccentricity 2

We consider the situation where $v_P\in H(F,2)$ for any special facet $F$. According to Table 1 we have $\eta =(d,d,d-2)$.

Proposition 35

Let $P$ be a $d$-dimensional simplicial, terminal, and reflexive $d$-polytope with exactly $3d-2$ vertices, where $d\ge 4$.

If ${{\mathrm{ecc}}}(P)=2$ then the polytope $P$ is lattice equivalent to either a skew bipyramid over a $(d{-}1)$-dimensional smooth Fano polytope with $3d-4$ vertices, or to the direct sum $P_5^{\oplus 2} \oplus P_6^{\oplus \frac{d}{2}-2}$. In the latter case $d$ is necessarily even.

Notice that $3d-4=(3d-2)-2=3(d-1)-1$, and therefore the possible bases of the bipyramids are explicitly known from Theorem 6.

Proof

Let $F$ be a special facet and $\phi \,{:}{=}\,\phi ^F$. Since $\eta _0=d$ Proposition 33 shows that $\mathrm{Vert }(F)$ is a lattice basis, and up to a unimodular transformation we may assume that $F={{\mathrm{conv}}}\{e_1,e_2,\ldots ,e_d\}$ and

$$\begin{aligned} V(F,0)&= \, \left\{ \phi (e_i)-e_i\,\right. \left| \,i\in [d]\right\} , \\ V(F,-1)&= \, \{-e_3,\, -e_4,\, \ldots ,\, -e_d\} . \end{aligned}$$

From Lemma 29 we know that $\phi (\phi (e_i))=e_i$ for all $i>2$. We distinguish whether or not $e_1$ or $e_2$ occur in the image of $\phi$.

Assume first that $|\{e_1,e_2\}\cap {{\mathrm{im}}}\phi |\le 1$. Then, up to symmetry, $e_1\not \in {{\mathrm{im}}}\phi$. Browsing our vertex lists above we see that the first coordinate is $0$ for all vertices except $e_1$ and $\phi (e_1)-e_1$. So $P$ is a skew bipyramid with apices $e_1$ and $\phi (e_1)-e_1$ over some $d-1$ dimensional polytope $Q$. By Lemma 3 it is a simplicial, terminal, and reflexive polytope with $3d-4$ vertices, and a smooth Fano polytope by Theorem 6.

It remains to consider the case $\{e_1, e_2\}\subset {{\mathrm{im}}}\phi$. If $\phi (e_r)=e_1$ for some $r\ne 1,2$, then $\phi (\phi (e_r))=e_r$ by Lemma 29. Thus, $\phi (e_1)=e_r$ and similarly for $e_2$. So either $\phi (e_1)=e_2$ and $\phi (e_2)=e_1$, or there are distinct $r, s\not \in \{ 1,2 \}$ with $\phi (e_r)=e_1$ and $\phi (e_s)=e_2$.

Assume first that $\phi (e_1)=e_2$ and $\phi (e_2)=e_1$. Then $\phi (e_i)\not \in \{e_1,e_2\}$ for all $i\ge 3$. The two-dimensional subspace spanned by $e_1$ and $e_2$ contains the four vertices $e_1, e_2, \pm (e_1-e_2)$ of $P$, while the remaining $3d-6=3(d-2)$ vertices of $P$ are contained in the subspace spanned by $e_3,e_4,\ldots ,e_d$. Hence, $P$ decomposes into a direct sum of a quadrangle and a $(d{-}2)$-dimensional polytope. But the quadrangle ${{\mathrm{conv}}}\{e_1, e_2, \pm (e_1-e_2)\}$ has $\mathbf 0$ in the boundary, so $P$ is not reflexive.

Hence, there exist distinct $r, s\not \in \{ 1,2 \}$ with $\phi (e_r)=e_1, \phi (e_s)=e_2, \phi (e_1)=e_r$, and $\phi (e_2)=e_s$. We conclude that $\phi$ is an involutory fixed-point free bijection on the set $\mathrm{Vert }(F)$. Therefore, $d$ must be even. Each linear subspace ${{\mathrm{lin}}}\{ e_i, \phi (e_i) \}$ intersects $P$ in a subspace containing $5$ or $6$ vertices, and all other vertices are in a complementary subspace. Thus, $P$ splits into

$$\begin{aligned} P\, = \ P_5^{\oplus 2}\oplus P_6^{\oplus \big (\frac{d}{2} - 2 \big )}, \end{aligned}$$

where the two copies of $P_5$ are contained in ${{\mathrm{lin}}}\{ e_1, e_r \}$ and ${{\mathrm{lin}}}\{e_2, e_s \}$. $\square$

Example 36

The 3-polytope $A$ from Example 13 satisfies the conditions stated in Proposition 35. The dimension is odd, and $A$ is a skew bipyramid over the lattice pentagon $P_5$.

5.2 Polytopes with Eccentricity 1

If the vertex sum $v_P$ lies on level one with respect to the special facet $F$, then $v_P$ is a vertex of $F$, as $P$ is terminal. By Table 1 we either have $\eta =(d,d,d-3,1)$ or $\eta =(d,d-1,d-1)$. The first case is the easier one; so we will treat it right away.

Proposition 37

Let $P$ be a $d$-dimensional simplicial, terminal, and reflexive polytope with exactly $3d-2$ vertices, where $d\ge 4$.

If the vertex sum $v_P$ is a vertex on a special facet $F$ with $\eta ^F=(d,d,d-3,1)$, then $P$ is lattice equivalent to a skew bipyramid over a $(d{-}1)$-dimensional smooth Fano polytope with $3d-4$ vertices.

Again we have $3d-4=3(d-1)-1$, and the possible bases of the bipyramids are classified in Theorem 6.

Proof

Let $\phi \,{:}{=}\,\phi ^F$. Proposition 33(i) shows that $\mathrm{Vert }(F)$ is a lattice basis, and we may assume that $F={{\mathrm{conv}}}\{e_1, e_2, \ldots , e_d\}$ as well as $v_P=e_1$. Furthermore,

$$\begin{aligned} V(F,0)=\left\{ \phi (e_i)-e_i\,\right. \left| \,i\in [d]\right\} \quad \text { and } \quad V(F,-1)\subseteq \left\{ -e_i\,\right. \left| \,i\in [d]\right\} . \end{aligned}$$

So $\phi (e_i)\ne \mathbf 0$ for all $i$, hence, by Lemma 29, if $-e_i$ is a vertex of $P$, then $\phi (\phi (e_i)) = e_i$. In this case, both $\phi (e_i)-e_i$ and $e_i-\phi (e_i)$ are vertices.

As $\eta _{-2}=1$ there is a unique vertex $z\in V(F,-2)$. Lemma 16 implies that $z_i \ge -1$ for all $i\in [d]$. If $z_j>0$ for some $j\ge 2$, then $z\in V(\mathrm{N }(F,e_j),k)$ for some $k \le -3$, as $\mathrm{N }(F,e_j)$ has normal $\mathbf 1-e_j$. Now $e_1\in \mathrm{N }(F,e_j)$, so $\mathrm{N }(F,e_j)$ is special. However, by Table 1 all possible $\eta$-vectors have $\eta _k=0$ for $k\le -3$, so $z_j\in \{-1,0\}$ for $j\ge 2$. Now consider

$$\begin{aligned} v_P \, = \, e_1 \ = \ z + \sum _{i=1}^{d} e_i + \sum _{i=1}^{d} (\phi (e_i)-e_i) + \sum _{i \in I} -e_i. \end{aligned}$$

for some index set $I\subset [d]$ with $|I|=d-3$. Solving for $z$ yields

$$\begin{aligned} z \ = \ e_1 - \sum _{i=1}^d \phi (e_i) + \sum _{i\in I} e_i. \end{aligned}$$

(9)

If $1\not \in I$ then $z_1\le 1$. If $1\in I$, then $-e_1$ is a vertex of $P$, so we know $\phi (\phi (e_1))=e_1$ by Lemma 29 and $e_1\in {{\mathrm{im}}}\phi$. So $e_1$ appears in both sums, and again $z_1\le 1$. Since $z_i \in \{ 0,-1 \}$ for all $i\ge 2$ we know that $z$ has (up to lattice equivalence) one of the following forms: either $z = -e_i - e_j$ for distinct $i,j \in [d]$ or $z = e_1 - e_2 -e_3 -e_4$.

$\begin{array}{|l|}\hline {\hbox {Let}\;z = -e_i - e_j.}\\ \hline \end{array}$ Assume that $[d]\setminus I=\{a,b,c\}$. If $\phi (e_r)=e_a$ holds for some $r$ then Eq. (9) implies $a \in \{ i,j \}$, and similarly for $b$ and $c$. Since $a, b$, and $c$ are pairwise distinct we have $\{a,b,c\}\not \subseteq \{i,j\}$. So at least one of the indices cannot appear in the image of $\phi$ and we may assume that $e_a\not \in {{\mathrm{im}}}\phi$. So $P$ can be written as a skew bipyramid with apices $e_a$ and $\phi (e_a)-e_a$ over some $(d{-}1)$-dimensional polytope $Q$ with $3d-4$ vertices. The polytope $Q$ is contained in linear hyperplane $x_a=0$. Lemma 2 implies the claim.

$\begin{array}{|l|}\hline {\hbox {Let}\;z = e_1 - e_2 -e_3 -e_4.}\\ \hline \end{array}$ In this case $-e_2,-e_3,-e_4 \notin P$ by Eq. (9). Let $J=\{2,3,4\}$. Then $I=[d]\setminus J$ and $J\subseteq {{\mathrm{im}}}\phi$. We further distinguish two cases.

• Assume first that there are indices $k,\ell \in J$ with $\phi (e_k)=e_\ell$. We may assume $k=3$ and $\ell =4$. By Eq. (9) $\phi$ is bijective, so $\phi (e_2) \ne e_4$. If also $\phi (e_2)\ne e_3$ then the primitive vector

  $$\begin{aligned} u \ = \ \bigl (2,0,-1, 1, 2, \ldots , 2\bigr ) \end{aligned}$$

  defines a valid inequality $\langle u,x\rangle \le 2$ for all $x\in P$. The $d-1$ vertices

  $$\begin{aligned} z , e_1, \phi (e_2)-e_2,\ -e_3 + e_4,\ e_5, \ldots ,\ e_d \end{aligned}$$

  satisfy $\langle u,x\rangle =2$, so $P$ would not be reflexive. If on the other hand $\phi (e_2)=e_3$ then by Lemma 28 the set

  $$\begin{aligned} G \, {:}{=} \, {{\mathrm{conv}}}\left( \left\{ e_k\,\right. \left| \,k\ne 2,3\right\} \;\cup \; \{ (-e_2+e_{3}),\, (-e_3+e_{4}) \} \right) \end{aligned}$$

  is a facet of $P$ with normal $u_G = \mathbf 1 -2e_2 -e_3$. But $\langle u_G, z \rangle = 1$, a contradiction.

• It remains to consider the case that $\phi (e_k)\ne e_\ell$ for all $k,\ell \in J$. The vector

  $$\begin{aligned} u' \, = \, (1,0,0,0,1,\ldots ,1) \end{aligned}$$

  defines a valid inequality $\langle u',x\rangle \le 1$. But then the $d+1$ vertices

  $$\begin{aligned} e_1,\ \phi (e_2)-e_2 ,\ \phi (e_3)-e_3 ,\ \phi (e_4)-e_4 ,\ e_4, \ldots ,\ e_d \end{aligned}$$

  span a facet which is not a simplex. $\square$

The remainder of this section deals with the situation where the $\eta$-vector reads $(d,d-1,d-1)$. By the previous proposition it suffices to consider polytopes whose $\eta$-vectors of all special facets agree.

Lemma 38

Let $P$ be a $d$-dimensional simplicial, terminal, and reflexive polytope with exactly $3d-2$ vertices such that $v_P$ is a vertex and $\eta =(d,d-1,d-1)$ for all special facets of $P$. Then there is a special facet $F$ with ${{\mathrm{opp}}}(F,v)\! \ne {{\mathrm{opp}}}(F,v_P)$ for all $v\in \mathrm{Vert }(F)\setminus \{ v_P \}$.

Proof

Pick any special facet $G$ and let $\phi \, {:}{=}\,\phi ^G$. If there is a vertex $w$ in $G$ with ${{\mathrm{opp}}}(G,w) \in V(G,-1)$ then we may take $F=G$, as no two vertices of $G$ share the same opposite vertex.

So assume that ${{\mathrm{opp}}}(G,w)\in V(G,0)$ for all $w\in \mathrm{Vert }(G)$. Let $w\in \mathrm{Vert }(G)\setminus \{v_P\}$. Then the neighboring facet $H\,{:}{=}\,\mathrm{N }(G,w)$ is special as it contains $v_P$. Suppose that the vertex $w$ is on level $-1$ with respect to $H$. Then, as above, we may take $F=H$.

We will refute all remaining cases. In view of our argument so far we can assume that for all vertices $w\in \mathrm{Vert }(G)\setminus \{v_P\}$ we have $\langle u_{\mathrm{N }(G,w)},w\rangle =0$; other choices for this value are ruled out by our assumption that the $\eta$-vectors of all special facets are equal to $(d,d-1,d-1)$. In this case we can assume by Proposition 33 that $\mathrm{Vert }(G)$ is a lattice basis, and, up to unimodular transformation, $G={{\mathrm{conv}}}\{e_1,e_2,\ldots , e_d \}$ as well as $v_P = e_1$ and, for some indices $a,b\not \in \{1,2\}$,

$$\begin{aligned} x \, {:}{=} \, {{\mathrm{opp}}}(G,e_1) \, = \, {{\mathrm{opp}}}(G,e_2) \, = -e_1 -e_2 +e_a +e_b\,. \end{aligned}$$

If $a=b$, then $x = -e_1 -e_2 +2 e_a$. So $H'\, {:}{=}\,\mathrm{N }(G,e_a)$ is a special facet with standard facet normal $u_{H'} = \mathbf 1 -e_a$. However, this means that $\langle u_{H'} , x\rangle = -2$ in contradiction to $\eta ^{H'}=(d,d-1,d-1)$. So $a\ne b$. In view of Proposition 33 we know

$$\begin{aligned} V(G,-1) \, \subseteq \ \{ -e_1,\, -e_2, \ldots , -e_d \} \;\cup \; \left\{ -e_1-e_2+e_r\,\right. \left| \,r\in [d]\right\} . \end{aligned}$$

Assume that the set $V(G,-1)$ contains a vertex $z=-e_1-e_2+e_r$ for some $r\ne 1,2$. Then, similar to the case above, the neighboring facet $\mathrm{N }(G,e_r)$ has standard facet normal $\mathbf 1-e_r$ implying that $z$ is at level minus two with respect to that facet. Again this is impossible. We conclude that $V(G,-1) \subseteq \left\{ -e_i\,\right. \left| \,i\in [d]\right\}$. Now $v_P=e_1$ requires that $-e_a$ and $-e_b$ both are vertices of $P$ and that $e_a,e_b \notin {{\mathrm{im}}}\phi$. By Lemma 28

$$\begin{aligned} H'' \ {:}{=} \ {{\mathrm{conv}}}\left( \left\{ e_k\,\right. \left| \,k\ne a,b\right\} \;\cup \; \{ \phi (e_a)-e_a,\, \phi (e_b)-e_b \} \right) \end{aligned}$$

is a facet which is also special, since $e_1 \in H$. But $x \in V(H'',-2)$, a contradiction.

Summarizing, this shows that we cannot have $\langle u_{\mathrm{N }(G,w)},w\rangle =0$ for all $w\in \mathrm{Vert }(G)\setminus \{v_P\}$. So there is no vertex $v$ of $G$ with ${{\mathrm{opp}}}(G,v_P) = {{\mathrm{opp}}}(G,v) \in V(G,0)$. We may thus take $F=G$. $\square$

We also need the following variation of the previous lemma.

Lemma 39

Let $P$ be a $d$-dimensional simplicial, terminal, and reflexive polytope with $3d-2$ vertices such that $v_P$ is a vertex and $\eta =(d,d-1,d-1)$ for all special facets of $P$. Then for some special facet $F$ there is $v\in \mathrm{Vert }(F)$ with ${{\mathrm{opp}}}(F,v)\in V(F,-1)$.

Proof

We prove this by contradiction, so assume that ${{\mathrm{opp}}}(G,v)\in V(G,0)$ for all special facets $G$ and vertices $v\in \mathrm{Vert }(G)$. Fix a special facet $G$ according to Lemma 38, so ${{\mathrm{opp}}}(G,v_P)\ne {{\mathrm{opp}}}(G,v)$ for all vertices $v$ of $\mathrm{Vert }(G)\setminus \{v_p\}$. By Proposition 33(iii) we can find a lattice transformation such that $G={{\mathrm{conv}}}\{ e_1,e_2,\ldots , e_d \}$ and with $\phi \,{:}{=}\phi ^G$ we have

$$\begin{aligned} V(G,0)&= \ \left\{ \phi (e_i)-e_i \,\right. \left| \, i\in [d] \setminus \{ 1,2 \} \right\} \;\cup \; \{ -e_1 -e_2 +e_a+e_b\}, \nonumber \\ V(G,-1)&\subseteq \ \{ -e_1,\, -e_2,\ldots , -e_d \} \;\cup \; \left\{ -e_1-e_2+e_r\,\right. \left| \,r\in [d]\right\} \end{aligned}$$

(10)

with $a,b \not \in \{ 1,2 \}$. By our choice of $G$ we know that $v_P$ is distinct from $e_1$ and $e_2$.

Assume first that $a\ne b$. Up to relabeling we can assume $v_P \ne e_a$ and $\phi (e_a)\ne e_1$. So $H {:}{=} \mathrm{N }(G,e_a)$ is still special. Further, $u_{H,e_1} = e_1$ and $u_H = \mathbf 1 - e_a$, so we observe that $e_a\in V(H,0)$. Now the assumption $\eta ^H = (d,d-1,d-1)$ implies $|V(G,0)\cap V(H,-1)|=|V(G,-1)\cap V(H,0)|$. Hence, $V(G,-1)\cap V(H,0)\subseteq \{-e_a\}$ and $-e_1 -e_2 +e_a +e_b \in V(G,0)\cap V(H,-1)$ shows $e_a \notin {{\mathrm{im}}}\phi$. So

$$\begin{aligned} V(H,0) \, = \, \left\{ \phi (e_i)-e_i \,\right. \left| \, i\in [d] \setminus \{ 1,2, a \} \right\} \cup \{e_a, -e_a\}\,. \end{aligned}$$

Therefore, $\langle u_{H,e_1}, y \rangle \ge 0$ for any $y\in V(H,0)$. Hence, ${{\mathrm{opp}}}(H,e_1)\notin V(H,0)$ by Proposition 20(ii) and we can choose $F=H$.

We are left with $a = b$. This implies $v_p = e_a = e_b$ as otherwise $\eta ^H_{-2}\ne 0$ for the special facet $H\,{:}{=}\,\mathrm{N }(G,e_a)$. We may assume that $a=3$. If $x\,{:}{=}\,-e_1-e_2+e_r\in V(G,-1)$ for some $r\ge 4$, then, as $H\,{:}{=}\,\mathrm{N }(G,e_4)$ is special, evaluating $\langle u_H,x\rangle =\langle \mathbf 1-e_r, x\rangle =-2$ contradicts the assumption $\eta ^H=(d,d-1,d-1)$. Further, there neither exists a vertex $x\in V(G,-1)$ with $\langle u_{G,v_p}, x \rangle >0$ since otherwise

$$\begin{aligned} \langle u_{G,v_P},v_P\rangle \ = \ \sum _{v\in \mathrm{Vert }(P)} \langle u_{G,v_P}, v \rangle \ \ge \ 2 \ > \ 1 . \end{aligned}$$

By Eq. (10) we have $V(G,-1) = \{-e_i\,|\,i\in [d] \setminus \{ k \}\}$ for some $k\in [d]$. We may assume that $k\ne 1$. So

$$\begin{aligned} u \, {:}{=} \ (2,-2,1,2,\ldots ,2) \end{aligned}$$

induces an inequality $\langle u,y\rangle \le 2$ valid for all $y\in P$. Furthermore, the vertices $e_1,e_4,e_5,\ldots , e_d, -e_2$, and $-e_1 -e_2 +2e_3$ satisfy this with equality, so $u$ defines a facet, contradicting the reflexivity of $P$. This proves the claim. $\square$

The previous result can now be extended to a characterization.

Proposition 40

Let $P$ be a $d$-dimensional simplicial, terminal, and reflexive polytope with exactly $3d-2$ vertices, where $d\ge 4$, such that $v_P$ is a vertex and $\eta ^G=(d,d-1,d-1)$ for every special facet $G$ of $P$.

Then $P$ is lattice equivalent to a (possibly skew) bipyramid over a $(d{-}1)$ dimensional smooth Fano polytope with $3d-4$ vertices.

Once again we have $3d-4=3(d-1)-1$, and the possible bases of the bipyramids are classified in Theorem 6.

Proof

By Lemma 39 and Proposition 33 we may assume $F={{\mathrm{conv}}}\{e_1,e_2,\ldots ,e_d\}$ is a special facet with (using $\phi \, {:}{=}\,\phi ^F$)

$$\begin{aligned} V(F,0)&= \, \left\{ \phi (e_i) - e_i\,\right. \left| \,i \in [d]\setminus \{ a \}\right\} \\ V(F,-1)&\subseteq \ S\, {:}{=}\, \{ -e_1,\,-e_2,\ldots , -e_d \} \\&\qquad \qquad \;\cup \;\left\{ -2e_a-e_r+e_s+e_t\,\right. \left| \,r,s,t \in [d] \text { p.d.},\, r\ne a\right\} \end{aligned}$$

for some unique index $a\in [d]$. Up to relabeling we can assume $v_P = e_1$. Let $x=-2e_a-e_r+e_s+e_t$ for some pairwise distinct $r,s,t$ with $r\ne a$. If $s\ne 1,a$, then $x$ would lie on level $-2$ for the special facet $\mathrm{N }(F,e_s)$. This is excluded by assumption. The same holds for $t$. So without loss of generality we may assume that $s=1$ and $t=a$, that is, $x = -e_a -e_r +e_1$ for some $r \in [d]$ and $r\ne 1,a$. We distinguish between $a=1$ and $a\ne 1$.

$\begin{array}{|l|}\hline {\hbox {Let}\; a=1.}\\ \hline \end{array}$ Then $V(F,-1) \subseteq S' \,{:}{=} \{ -e_1,-e_2, \ldots , -e_d \}$ and $z\, {:}{=} {{\mathrm{opp}}}(F,e_1) = {{\mathrm{opp}}}(F,e_a) \in V(F,-1)$. This implies that $\langle u_{F,e_1}, z \rangle < 0$. The only vertex in $S'$ that satisfies this is $-e_1$, so $z=-e_1$. Since $\eta _{-1}=d-1$ up to relabeling we have

$$\begin{aligned} V(F,-1) \ = \ \{ -e_1,\, -e_2,\ldots , -e_{d-1} \}. \end{aligned}$$

$v_P=\mathbf 0$ requires that $e_d \notin {{\mathrm{im}}}\phi$, and thus $P$ is a skew bipyramid with apices $e_d$ and $\phi (e_{d}) - e_d$ over some $(d-1)$ dimensional polytope $Q$ with $3d-4$ vertices. By Lemma 2 we know that $Q$ is again simplicial, terminal, and reflexive. This is the claim.

$\begin{array}{|l|}\hline {\hbox {Let}\; a\ne 1.}\\ \hline \end{array}$ Let $z\, {:}{=}{{\mathrm{opp}}}(F,e_a) \in V(F,-1)$. As before we have $\langle u_{F,e_a}, z \rangle <0$. Among the points in $S$ this is only satisfied by $-e_a$ and $-e_a-e_r+e_1$ for some $r\in [d]\setminus \{ 1,a \}$. In either case the facet normal of $F' = \mathrm{N }(F,e_a)$ is $u_{F'} = \mathbf 1 -2e_a$, so only one of those points can be in $V(F,-1)$. Hence, $V(F,-1) \subseteq \{ -e_1,-e_2,\ldots , -e_d \} \cup \{ z \}$. Using $v_P=\mathbf 0$ we see that $e_a \not \in {{\mathrm{im}}}\phi$.

If $z = -e_a$ we conclude that $P$ is a proper bipyramid over a $(d-1)$-dimensional smooth Fano polytope $Q$ with $3d-4$ vertices. The polytope $Q$ is the intersection of $P$ with the hyperplane $x_a = 0$.

If $z = -e_a -e_r +e_1$ for some $r\in [d]\setminus \{ 1,a \}$ and $\phi (e_r)=e_1$ we get a skew bipyramid with apices $e_a$ and $z$ (because the line segment between $e_a$ and $z$ intersects with the hyperplane $x_a = 0$ in the interior of $P$).

We will show that the remaining case $z = -e_a -e_r +e_1$ for some $r\in [d]\setminus \{ 1,a \}$ and $\phi (e_r)\ne e_1$ does not occur. We claim that $-e_r \notin P$. Let $F^{(r)} = \mathrm{N }(F,e_r)$. The facet normal reads $u_{F^{(r)}} = \mathbf 1 - e_r$, so that $z,\, -e_r \in H(F^{(r)}, 0)$. Further, we have $u_{F^{(r)},\phi (e_r)} = \phi (e_r)+e_r$. Lemma 16 together with $\langle u_{F^{(r)},\phi (e_r)}, z \rangle = -1$ show that $z={{\mathrm{opp}}}(F^{(r)},\phi (e_r))$. If $-e_r\in P$, then, by the same argument, ${{\mathrm{opp}}}(F^{(r)},\phi (e_r))=-e_r$. Hence, $-e_r\not \in P$, and

$$\begin{aligned} V(F,-1) \ = \ \left\{ -e_i\,\right. \left| \,i\in [d] \setminus \{a,r\}\right\} \cup \{ z \}. \end{aligned}$$

Now $e_a\not \in {{\mathrm{im}}}\phi , e_r \in {{\mathrm{im}}}\phi$ and Lemma 29 shows that $\phi (\phi (e_i)) = e_i$ for all $i\in [d] \setminus \{ a \}$.

Let $u\, {:}{=}\mathbf 1 -e_1 -3e_r -2\phi (e_{r})$. Inspecting $V(F,0)$ and $V(F,-1)$, we see that the inequality $\langle u, x \rangle \le 1$ is valid for $P$ (recall that $\eta ^F_{k}=0$ for $k\le -2$). $u$ induces a face

$$\begin{aligned} G \ {:}{=} \ {{\mathrm{conv}}}( (\mathrm{Vert }(F)\setminus \{ e_1,\, e_r,\, \phi (e_r) \}) \;\cup \; \{ z,\, -\phi (e_r),\, \phi (e_r)-e_r,\, \phi (e_1)-e_1 \} ) \end{aligned}$$

that is actually a facet. However, it contains $d+1$ vertices, so it is not a simplex. This is the desired contradiction. $\square$

5.3 Polytopes with Eccentricity 0

This is equivalent to $v_P=\mathbf 0$, which makes every facet a special facet. This situation is the most difficult by far. We start out with a general characterization of the centrally symmetric case. For this result we neither make any assumption on the number of vertices nor on the terminality.

Proposition 41

Let $P$ be a simplicial and reflexive polytope. Then $P$ is centrally symmetric if and only if $v_P=\mathbf 0$ and $\eta ^G_\ell = 0$ for every facet $G$ and any $\ell \le -2$. In other words: the polytope $P$ is centrally symmetric if and only if it’s lattice width in each facet direction is equal to $2$.

Proof

Assume first that $v_P=\mathbf 0$ and $\eta ^G_\ell = 0$ for every facet $G$ and any $\ell \le -2$. Let $\langle u, x \rangle \le 1$ be a facet defining inequality. Our assumption on the $\eta$-vectors implies that $\langle -u, x \rangle \le 1$ is a valid inequality. Take a vertex $v$ and look at its antipode $-v$. If $-v\not \in P$ then there is a facet defining inequality which separates $-v$ from $P$. By the above argument there would be a valid inequality separating $v$ from $P$, which is impossible. Therefore, the point $-v$ is contained in $P$. Further, since $-v$ satisfies at least $d$ linearly independent valid inequalities with equality it must be vertex. The converse direction is obvious. $\square$

The centrally symmetric smooth Fano polytopes are listed in Theorem 4 which sums up results of Voskresenskĭ and Klyachko [21], Ewald [9, 10] and Nill [16, 17].

Corollary 42

Let $P$ be a $d$-dimensional polytope simplicial, terminal, and reflexive polytope with exactly $3d-2$ vertices. If $P$ is centrally symmetric then it is lattice equivalent to

• (i) a double proper bipyramid over $P_6^{\oplus \frac{d-2}{2}}$ or

• (ii) $\mathrm{DP }(4) \oplus P_6^{\oplus \frac{d}{2} - 2}$.

Proof

A centrally symmetric, simplicial, and reflexive polytope $P$ is a direct sum of centrally symmetric cross polytopes and del Pezzo polytopes. A $k$-dimensional cross polytope has $2k$ vertices. A $k$-dimensional del Pezzo polytope has $2k+2$ vertices (and $k$ is even by definition of del Pezzo polytopes), while a $k$-dimensional pseudo del Pezzo polytope has $2k+1$ vertices (and again, $k$ must be even). The latter is not centrally symmetric, so no direct sum involving it will be.

We need to find those direct sums of these three types of polytopes that have $3d-2$ vertices in dimension $d$. On average, for each dimension the polytope must have $3-\frac{2}{d}$ vertices. This is only possible if at most 2 of the summands are not $2$-dimensional del Pezzo polytopes. This leaves us with direct sums of $2$-dimensional del Pezzo polytopes with one $2$-dimensional cross polytope, or $\mathrm{DP }(4)$. $\square$

We first establish a further restriction on the $\eta$-vectors. This says that the $\eta$-vector in the fourth column of Table 1 does not occur. Notice that, if $d=2$ in Corollary 42 then $d-2=0$ and $P^{\oplus \frac{d-2}{2}}$ is the origin. In this case the only polytope of type (i) is the regular cross-polytope $P_{4a}$ shown in Fig. 1c; this is centrally symmetric.

Proposition 43

Let $P$ be a simplicial and reflexive $d$-polytope with exactly $3d-2$ vertices satisfying $v_P=\mathbf 0$. Then $\eta ^G_\ell =0$ for all $\ell \le -3$ and for each facet $G$.

Proof

We fix a facet $G$ and abbreviate $\eta =\eta ^G$ and $\phi \, {:}{=}\phi ^G$. Now suppose that $\eta _{-\ell }>0$ for some $\ell \le -3$. According to Table 1 then $\ell =-3$ and $\eta =(d,d,d-3,0,1)$. Let $z$ be the unique vertex in $V(G,-3)$. We are aiming at a contradiction.

By Proposition 33 (i) we may assume that $G={{\mathrm{conv}}}\{ e_1,e_2,\ldots , e_d \}$ and (up to relabeling)

$$\begin{aligned} V(G,0) = \left\{ \phi (e_i)-e_i\,\right. \!\!\left| \,i\in [d]\right\} \quad \text { and } \quad V(G,-1) = \{-e_1, -e_2, \ldots , -e_{d-3}\}. \end{aligned}$$

In this situation Lemma 29 shows $\phi (\phi (e_i))=e_i$ for $1\le i\le d-3$ and hence $\{e_i\,|\,i\in [d-3]\} \subseteq {{\mathrm{im}}}\phi$. The condition $v_P=\mathbf 0$ tells us that

$$\begin{aligned} z\ + \ \sum _{i=1}^d \phi (e_i) \ +\ \sum _{i=1}^{d-3} -e_i \ =\ 0\,. \end{aligned}$$

(11)

Hence, $z = -e_i-e_j-e_k$ for some $i,j,k\in [d]$. Suppose that $j=k$. Then the midpoint

$$\begin{aligned} \frac{1}{2}z + \frac{1}{2}e_i \ = \ \frac{1}{2}(-e_i-2e_j)+\frac{1}{2}e_i \ = \ -e_j \end{aligned}$$

of the line segment between $z$ and $e_i$ is a non-zero lattice point in $P$ that is not a vertex. This contradicts terminality of $P$. We conclude that the indices $i,j,k$ are pairwise distinct. Two cases may occur.

$\begin{array}{|l|}\hline {\hbox {Let}\;z\ne -e_{d-2}-e_{d-1}-e_d.}\\ \hline \end{array}$ Choose $a\in \{d-2,d-1,d\}\setminus \{i,j,k\}$. Then $-e_a\not \in P$. Hence, by Eq. (11) we know ${{\mathrm{im}}}\phi = \{ e_1,e_2,\ldots , e_{d-3} \} \cup \{ e_i,e_j,e_k \}$ and $e_a \notin {{\mathrm{im}}}\phi$. Thus, $x_a=0$ for every vertex $x\in V(G,0) \setminus \{ \phi (e_a)-e_a \}$.

We conclude that $P$ is a skew bipyramid with apices $e_a$ and $\phi (e_a)-e_a$ over $Q= \{x\in P\,|\,x_a=0\}$, and $Q$ is a simplicial, terminal, and reflexive $(d{-}1)$-polytope with $3d-4$ vertices. The face $H\, {:}{=}\,G\cap Q$ is a facet of $Q$. With respect to $H$ the vertex $z\in Q$ is still on level $-3$. However, we can check using Øbro ’s classification given in (1), (2), and (3) that no facet (also the non-special ones) of a simplicial, terminal, and reflexive polytope with $3d-1$ vertices has a vertex on level $-3$. To check this, observe that it suffices to look at each summand of the given representation separately. Those are $P_5, P_6$, and the proper and skew bipyramid over $P_6$. Thus, there is no such polytope $Q$ that could serve as a basis for the skew bipyramid $P$.

$\begin{array}{|l|}\hline {\hbox {Let}\;z=-e_{d-2}-e_{d-1}-e_d.}\\ \hline \end{array}$ In this case Eq. (11) implies that $\phi$ is bijective. We have $\phi (\phi (e_i))=e_i$ for $1\le i\le d-3$ as well as $\phi (e_i)\not \in \{ 0, e_i\}$ for all $i \in [d]$. Up to relabeling we are left with three possibilities:

• $\phi (e_{d-2}),\phi (e_{d-1}),\phi (e_d) \in \{ e_1,e_2,\ldots , e_{d-3} \}$: Then $P$ is the direct sum of two polytopes $Q\subset {\mathbb {R}}^{6}$ and $R \subset {\mathbb {R}}^{d-6}$, where $Q$ is the convex hull of the 16 points

  $$\begin{aligned}&\qquad \qquad \qquad e_1,\ e_2, \ldots , e_6\\&\pm (e_1 - e_4), \pm (e_2 - e_5), \pm (e_3 - e_6)\\&\qquad \qquad \qquad -e_1, -e_2, -e_3\\&\qquad \qquad \qquad -e_4-e_5-e_6 . \end{aligned}$$

  However, $Q$ is not simplicial as the vector $(1,1,-1,0,1,-2)$ induces a facet with seven vertices.

• $\phi (e_{d-2}) \in \{ e_1,e_2,\ldots , e_{d-3} \}, \phi (e_d)=e_{d-1}$, and $\phi (e_{d-1})=e_d$: Then $P$ is the direct sum of two polytopes $Q\subset {\mathbb {R}}^{4}$ and $R \subset {\mathbb {R}}^{d-4}$, where $Q$ is the convex hull of the ten points

  $$\begin{aligned} e_1, e_2, e_3, e_4;\quad \pm (e_1 - e_2), \pm (e_3 - e_4);\quad -e_1;\quad -e_2-e_3-e_4 . \end{aligned}$$

  Again $Q$ is not simplicial as the vector $(-1,-2,0,1)$ induces a facet with four vertices.

• $\phi (e_{d-2})=e_{d-1}, \phi (e_{d-1})=e_d$, and $\phi (e_d)=e_{d-2}$: Then $P$ is the direct sum of two polytopes $Q\subset {\mathbb {R}}^{3}$ and $R \subset {\mathbb {R}}^{d-3}$, where $Q$ is the convex hull of the ten points

  $$\begin{aligned} e_1, e_2, e_3;\quad \pm (e_1 - e_2), \pm (e_2 - e_3), \pm (e_3 - e_1);\quad -e_1-e_2-e_3 . \end{aligned}$$

  For $u=(-1, 2, -4)$ the inequality $\langle u,x\rangle \le 3$ induces a triangular facet of $Q$ with vertices $-e_1+e_2, -e_3+e_1$, and $-e_1-e_2-e_3$. This means that $Q$ is not reflexive. $\square$

In view of Table 1 the preceding result leaves $(d,d,d-4,2), (d,d-1,d-2,1)$ or $(d,d-2,d)$ as choices for the $\eta$-vector of any special facet. As Proposition 41 and Corollary 42 deal with the case that every facet has $\eta$-vector $\eta =(d,d-2,d)$ only two cases remain.

We will look at the situation where $v_P=\mathbf 0$ and there is a special facet $F$ with $\eta =(d,d-1,d-2,1)$. Since $\eta _{0}=d-1$ we know that there is at least one vertex $v\in F$ with $\phi (v)=\mathbf 0$. Otherwise the opposite vertex of $v$ would be $\phi (v) -v \in V(F,0)$ for every choice of $v$ which would imply $\eta _{0}=d$. One technical difficulty in our proof is that we will have to distinguish whether the vertex ${{\mathrm{opp}}}(F,v)$ lies on level $0, -1$ or $-2$ with respect to $F$. If ${{\mathrm{opp}}}(F,v)$ lies on a level below $0$, all the other vertices $w$ of $F$ are good with $\phi (w)\ne \mathbf 0$. These cases are easier, and we will deal with them first. The remaining case where $\eta = (d,d,d-4,2)$ will be reduced to one of the cases above.

Lemma 44

Let $P$ be a simplicial, terminal, and reflexive $d$-polytope with exactly $3d\!-\!2$ vertices such that $v_P=\mathbf 0$ and there is a special facet $F$ with $\eta =(d,d-1,d-2,1)$. If the unique vertex at level $-2$ with respect to $F$ is opposite to some vertex in $F$ then $P$ is lattice equivalent to a skew bipyramid over a $(d-1)$-dimensional smooth Fano polytope with $3d-4$ vertices.

Proof

By Proposition 33(iii) we may assume $F = {{\mathrm{conv}}}\{ e_1, e_2, \ldots , e_d \}$, and, up to relabeling, $z \, {:}{=} {{\mathrm{opp}}}(F,e_1) \in V(F,-2)$ as well as (with $\phi \, {:}{=}\,\phi ^F$)

$$\begin{aligned} V(F,0)&= \ \left\{ \phi (e_i)-e_i\,\right. \left| \,i\in [d]\setminus \{ 1 \}\right\} , \nonumber \\ V(F,-1)&= \ \left\{ -e_i\,\right. \left| \,i\in [d]\right\} \;\cup \; \left\{ -2e_1-e_r+e_s+e_t\,\right. \left| \,r,s,t\in [d] \text { p.d.},\, r\ne 1\right\} \end{aligned}$$

(12)

If $z_i=\langle u_{F,e_i}, z \rangle$ is positive for some $i\ge 2$, then $z\in V(\mathrm{N }(F,e_i),-3)$. But $\mathrm{N }(F,e_i)$ is special, so this contradicts Proposition 43. Moreover, $z={{\mathrm{opp}}}(F,e_1)$ implies $z_1<0$ by Lemma 16. Hence $z=-e_1 -e_k$ for some $k\in [d]$, and $k\ne 1$ as $z$ is primitive. Up to relabeling we may assume that $k=2$. The standard facet normal of the facet $F' \,{:}{=}\,\mathrm{N }(F,e_1)$ is $u_{F'}=(-2,1,\ldots , 1)$. Evaluating this on the right hand side of Eq. (12) shows that $V(F,-1)$ is already contained in the reduced set

$$\begin{aligned} V(F,-1)\ \subseteq \ \{ -e_2, -e_3, \ldots , -e_d \} . \end{aligned}$$

Using the fact that $v_P=0$ we know that, in particular, the first coordinates of all vertices sum to zero. We conclude that the map $\phi$ does not attain the value $e_1$. Thus, $P$ is a skew bipyramid with apices $e_1$ and $z=-e_1-e_2$ over the polytope $Q=\{y\in P\,|\,y_1=0\}$. Those are classified in Theorem 6. $\square$

Example 45

The facet $H={{\mathrm{conv}}}\{e_2, e_3, e_4, e_2-e_1\}$ of the 4-polytope $B$ from Example 14 has facet normal $u_H=-e_2-e_3-e_4=\mathbf 1-e_1$. Hence, it satisfies the conditions of Lemma 44: the unique vertex $e_1-e_2-e_3$ at level $-2$ with respect to $H$ is opposite to $e_3$. As pointed out previously, $B$ is a skew bipyramid over $P_5$.

The following gives a, slightly technical, sufficient condition for the existence of a pair of distant vertices, unless the polytope is a skew bipyramid.

Lemma 46

Let $P$ be a simplicial, terminal, and reflexive $d$-polytope with exactly $3d-2$ vertices such that $v_P=\mathbf 0$ and $F = {{\mathrm{conv}}}\{ e_1, e_2, \ldots , e_d \}$ is a special facet with $\eta = (d, d-1, d-2,1)$. If there exist pairwise distinct indices $r,s,t\in [d]$ with ${{\mathrm{opp}}}(F,e_r) = -e_r-e_s+e_t$ then the vertices $e_r$ and ${{\mathrm{opp}}}(F,e_r)$ are distant, or $P$ is a skew bipyramid over some smooth Fano $(d{-}1)$-polytope with $3d-4$ vertices.

Proof

We fix $\phi \, {:}{=}\,\phi ^F$. Up to relabeling we may assume that $(r,s,t)=(1,2,3)$. Then $\phi (e_1)=\mathbf 0$ as $x\,{:}{=}{{\mathrm{opp}}}(F,e_1)=-e_1-e_2+e_3$ does not lie on level $0$. According to Proposition 33 we get,

$$\begin{aligned} V(F,0)&= \{ \phi (e_2)-e_2, \phi (e_3)-e_3, \ldots , \phi (e_d)-e_d \},\nonumber \\ V(F,-1)&\subseteq \left\{ -e_i\,\right. \left| \,i\in [d]\right\} \cup \{ x \}. \end{aligned}$$

(13)

Let $z$ be the unique vertex at level $-2$. Proposition 43 implies that $z$ only has non-positive coefficients. Otherwise we would look at the special facet $\mathrm{N }(F,e_i)$ with $i$ being the index of the positive coefficient. Lemma 16 tells us that in this case $z$ must lie on a level below $-2$ with respect to $\mathrm{N }(F,e_i)$. So we can assume $z= -e_k - e_\ell$ for some indices $k, \ell$. Terminality and $e_k \in {{\mathrm{conv}}}\{ z, e_\ell -e_k\}$ implies $\phi (e_k)\ne e_\ell$. Similarly, $\phi (e_\ell )\ne e_k$.

We give a brief outline of the proof. By Lemma 18, the vertices $e_1$ and ${{\mathrm{opp}}}(F,e_1)$ are distant if and only if $e_1+{{\mathrm{opp}}}(F,e_1)=-e_2+e_3$ is a vertex of $P$ and $\phi (e_2)=e_3$. So our goal is to show that if $\phi (e_2) \ne e_3$ the polytope $P$ is a skew bipyramid. We start out by reducing the possible choices for $\phi (e_2)$ and $\phi (e_3)$. In particular, we will show that $\phi (e_2) \ne e_1$ and $\phi (e_3) \in \{ e_1, e_2 \}$. Then we will distinguish between the two choices for $\phi (e_3)$. By counting and using that $v_P=\mathbf 0$ we will be able to deduce the precise shapes of $V(F,-1)$ and $z$. This will give a complete description of the polytope $P$. A direct computation will finally show that $P$ is not simplicial, unless it is a skew bipyramid.

Suppose $\phi (e_2)=e_1$. Then $e_1-e_2=\phi (e_2)-e_2$ is a vertex of $P$. If $e_1$ and $x$ are not distant, then there is a facet $G$ that contains $e_1$ and $x$. Its facet normal $u_G$ satisfies $\langle u_G,e_1\rangle =\langle u_G,x\rangle =1$ and $\langle u_G,e_1-e_2\rangle , \langle u_G, e_3\rangle \le 1$, so

$$\begin{aligned} 1\ge \langle u_G, e_1-e_2\rangle \ = \, \langle u_g, e_1\rangle + \langle u_G, x\rangle +\langle u_G, e_1-e_3\rangle \ = \, 1+1+1-\langle u_G, e_3\rangle \ \ge \ 2, \end{aligned}$$

a contradiction. Hence, $\phi (e_2)\ne e_1$.

If $\phi (e_2)=e_3$ then $e_1+x=-e_2+e_3=\phi (e_2)-e_2$, in which case $e_1$ and $x={{\mathrm{opp}}}(F,e_1)$ are distant due to Lemma 18. So we may assume that $\phi (e_2)\ne e_3$, and up to relabeling we can set $\phi (e_2) = e_4$.

Next we will show that $\phi (e_3) \in \{ e_1,e_2 \}$. Consider the facet $F^{(3)}=\mathrm{N }(F,e_3)$. Its vertices are $e_i$ for $i\ne 3$ and $\phi (e_3)-e_3$, so the vertices of $F^{(3)}$ form a lattice basis. Writing $x$ in this basis gives

$$\begin{aligned} x \ = \ -e_1 -e_2 - (\phi (e_3) - e_3) + \phi (e_3). \end{aligned}$$

Since $x \in V(F^{(3)}, -2)$ we know from Proposition 43 that $x$ has no positive coefficient with respect to this basis (as above, we can see that otherwise $x$ is at level $-3$ for any neighboring facet corresponding to a coordinate with positive coefficient). Hence, $\phi (e_3)$ must cancel with one of $-e_1$ or $-e_2$, so $\phi (e_3) \in \{ e_1, e_2 \}$.

We determine the vertices in $V(F,-1)$. The normal vector of $F^{(1)}=\mathrm{N }(F,e_1)={{\mathrm{conv}}}(x,e_2, \ldots , e_d)$ is $u_{F^{(1)}} = \mathbf 1 - 2e_1$. Hence, if $-e_1\in \mathrm{Vert }(P)$, then $-e_1\in F^{(1)}$ and $F^{(1)}$ would contain more than $d$ vertices. So $-e_1\not \in \mathrm{Vert }(P)$. Now consider $F^{(2)}={{\mathrm{conv}}}(e_1, e_4-e_2, e_3, \ldots , e_d)$. Then $u_{F^{(2)}, e_4}=e_2+e_4$, so

$$\begin{aligned} \langle u_{F^{(2)}, e_4}, x\rangle = -1 \qquad \langle u_{F^{(2)}}, x\rangle \ = \, 0. \end{aligned}$$

By Proposition 20(ii) this implies ${{\mathrm{opp}}}(F^{(2)}, e_4)=x$, and

$$\begin{aligned} F^{(2,4)}\, {:}{=}\, \mathrm{N }(\mathrm{N }(F,e_2), e_4) = {{\mathrm{conv}}}\left( \left\{ e_i\,\right. \left| \,i\in [d]\setminus \{ 2,4 \}\right\} \cup \{ (e_4-e_2),\, x\}\right) . \end{aligned}$$

Hence, $u_{F^{(2,4)}} = \mathbf 1 -2e_2 -e_4$. As $\langle u_{F^{(2,4)}}, -e_2 \rangle =1$ and $-e_2\not \in \mathrm{Vert }(F^{(2,4)})$ we know that $-e_2\not \in V(F,-1)$. For the remaining part of our proof we will distinguish between $\phi (e_3)=e_1$ and $\phi (e_3)=e_2$.

$\begin{array}{|l|}\hline {\hbox {Let}\;\phi (e_3)= e_1.}\\ \hline \end{array}$ We list the vertices already known to have a non-vanishing first coordinate:

$$\begin{aligned} e_1 , \quad -e_1 -e_2 + e_3 , \quad e_1-e_3. \end{aligned}$$

From $v_P = \mathbf 0$ we learn that there must exist at least one more vertex with a negative first coordinate. By (13) and $-e_1\not \in P$ the only possibility is $k=1$, which means $z=-e_1 -e_\ell$. This also implies that $\phi (e_i) \ne e_1$ for $i\ne 3$. Now we list the vertices already known to have a non-zero third coordinate:

$$\begin{aligned} e_3 , \quad e_1 -e_3 , \quad -e_1 -e_2 +e_3. \end{aligned}$$

This tells us that there must exist another vertex with a negative third coordinate. There are two possibilities; either $-e_3\in \mathrm{Vert }(P)$ or $\ell =3$, i.e. $z =-e_1 -e_3$. As $-e_3=\tfrac{1}{2}((-e_1-e_3)+(e_1-e_3))$ and $\phi (e_3)=e_1$ the polytope $P$ is not terminal in the latter case. So $k\ne 3, -e_3\in \mathrm{Vert }(P)$, and there is exactly one index $j\ne 1,2,3$ such that

$$\begin{aligned} V(F,-1) \ = \ \left\{ -e_i\,\right. \left| \,i\in [d]\setminus \{ 1,2,j \}\right\} \,\cup \, \{ x \}. \end{aligned}$$

We list all the vertices known to have a non-vanishing $j$-th coordinate:

$$\begin{aligned} e_j , \quad \phi (e_j) - e_j . \end{aligned}$$

If $e_j\not \in {{\mathrm{im}}}\phi$ these are the only two vertices with this property, and hence $P$ is a skew bipyramid with apices $e_j$ and $\phi (e_j)-e_j$. So in the following we may assume that $e_j \in {{\mathrm{im}}}\phi$. Hence, $\ell =j$, that is, $z= -e_1 -e_j$. We will distinguish between $j=4$ and $j\ne 4$. The aim is to write $P$ as a sum of two polytopes $P= Q\oplus R$ where we can show that $Q$ is not simplicial.

Consider first the case $j=4$. By Lemma 29 $\phi (\phi (e_i))\in \{\mathbf 0, e_i\}$ if $-e_1\in \mathrm{Vert }(P)$, so $\phi (e_i)\ne e_2$ for $i\ne 1,2,4$, as $\phi (e_2)=e_4$. As $v_P=\mathbf 0$ implies $e_2\in {{\mathrm{im}}}\phi$ we deduce $\phi (e_4)=e_2$. By the same lemma, and using $\phi (e_i)\ne e_1$ for $i\ne 3$ as well as $-e_i\in \mathrm{Vert }(P)$ for $i\ge 5$ we obtain $\phi (\phi (e_i))=e_i$ for $i\ge 5$. Hence, $\phi (e_i)\not \in \{ e_1,e_2,e_3,e_4 \}$. We can write $P = Q \oplus P_6^{\oplus \frac{d-4}{2}}$ where $Q$ is the convex hull of the ten points:

$$\begin{aligned}&\qquad \quad e_1 , e_2 , e_3 , e_4 ,\\&e_4-e_2 , e_1-e_3, e_2 - e_4 ,\\&\quad \,\, -e_1-e_2+e_3 , -e_3,\\&\quad \quad \qquad \,\, -e_1 -e_4 . \end{aligned}$$

$Q$ is not simplicial as $u = (1,-1,1,-2)$ induces a facet which is not a simplex. Hence, $P$ would not be simplicial.

So we may assume that $j \ne 4$. So, up to relabeling $j=5$. We list the vertices known to have a non-zero fourth coordinate:

$$\begin{aligned} e_4 , \quad \phi (e_4) - e_4 ,\quad e_4 - e_2 , \quad -e_4 . \end{aligned}$$

From Lemma 29 it follows that $\phi (\phi (e_4))=e_4$. So the only possible way to maintain $v_P = \mathbf 0$ is that $\phi (e_4)=e_2$. We have already seen that $\phi (e_j)\ne e_5$ for $j\le 4$. By assumption, $e_5 \in {{\mathrm{im}}}\phi$, so there is some $j\ge 6$ such that $\phi (e_j) = e_5$. Now $-e_j \in \mathrm{Vert }(P)$ implies $\phi (e_5) = e_j$, so $j$ is unique and we can assume that $j=6$. This leaves us with $P= Q \oplus P_6^{\oplus \frac{d-6}{2}}$, where $Q$ is the convex hull of

$$\begin{aligned}&\qquad \qquad \qquad e_1 , e_2 , e_3 , e_4 , e_5 , e_6 ,\\&e_4-e_2 , e_1-e_3 , e_2-e_4 , e_6-e_5 , e_5 - e_6,\\&\qquad -e_1-e_2+e_3 , -e_3 , -e_4 , -e_6 ,\\&\qquad \qquad \qquad \qquad -e_1 -e_5. \end{aligned}$$

The polytope $Q$ is not simplicial as the vector $u = (1,-2,0,-1,-2,-1)$ induces a facet which is not a simplex. This is a contradiction to $P$ being simplicial, and this concludes the case $\phi (e_3)=e_1$.

$\begin{array}{|l|}\hline {\hbox {Let}\; \phi (e_3)= e_2.}\\ \hline \end{array}$ The argument is similar to the other case. Using Lemma 29, $-e_3 \in \mathrm{Vert }(P)$ would imply $\phi (e_2) = \phi (\phi (e_3))= e_3$ which contradicts the assumption $\phi (e_2) = e_4$. Hence,

$$\begin{aligned} V(F,-1) \ = \ \left\{ -e_i\,\right. \left| \,i\in [d]\setminus \{ 1,2,3 \}\right\} \,\cup \, \{ x \}. \end{aligned}$$

We list the vertices known to have a non-vanishing third coordinate:

$$\begin{aligned} e_3 ,\quad e_2 -e_3 ,\quad -e_1 -e_2 +e_3. \end{aligned}$$

Again $v_P=\mathbf 0$ implies that $k=3$, that is, $z = -e_3 -e_\ell$ for some $\ell$ and $e_3 \not \in {{\mathrm{im}}}\phi$. We have seen above that $\phi (e_3) = e_2$ implies $\ell \ne 2$.

If $\phi (e_4) = e_2$, then, using $\ell \ne 2$ and $-e_2\not \in \mathrm{Vert }(P)$, we have the following vertices with a non-zero second coordinate:

$$\begin{aligned} e_2 ,\quad e_4 -e_2 ,\quad e_2 - e_4. \end{aligned}$$

This violates $v_P = \mathbf 0$, so $\phi (e_4)\ne e_2$.

We consider $\phi (e_4) = e_1$ and $\phi (e_4) \ne e_1$ separately. In the former case, by counting all vertices with a non-zero first coordinate

$$\begin{aligned} e_1 ,\quad -e_1 -e_2 +e_3 ,\quad e_1 -e_4 , \end{aligned}$$

we see that $\ell =1$, that is, $z=-e_1 -e_3$. Therefore, $P=Q \oplus P_6^{\oplus \frac{d-4}{2}}$ for the convex hull $Q$ of the points

$$\begin{aligned}&e_1, e_2, e_3, e_4 ,\\&e_4-e_2, e_2-e_3, e_1 - e_4,\\&-e_1-e_2+e_3, -e_4,\\&-e_1 -e_3 . \end{aligned}$$

The polytope $Q$ is not simplicial as $u = (1, -1, 1, 0)$ induces a facet which is not a simplex. Again, this contradicts that $P$ is simplicial.

We are left with $\phi (e_4)\ne e_1$. As argued above $\phi (e_4)\ne e_2$ and as $\phi (\phi (e_4))=e_4$ due to Lemma 29 we have that $\phi (e_4)\ne e_3$. So we may assume $\phi (e_4)=e_5$. Examining all known vertices with a non-zero fourth coordinate, namely,

$$\begin{aligned} e_4 ,\quad e_5 - e_4 ,\quad e_4 -e_5 ,\quad e_4 - e_2 ,\quad -e_4 , \end{aligned}$$

we see that $z=-e_3-e_4$. We can split $P$ into the sum $Q\oplus P_6^{\oplus \frac{d-5}{2} }$, where $Q$ is the convex hull of

$$\begin{aligned}&e_1, e_2, e_3, e_4, e_5,\\&e_4-e_2, e_2-e_3, e_5 - e_4, e_4 -e_5,\\&-e_1-e_2+e_3, -e_4, -e_5,\\&-e_3 -e_4. \end{aligned}$$

The polytope $Q$ is not simplicial as $u = (1,1,0,0,-1,0)$ induces a facet which is not a simplex. Once again, this is a contradiction to $P$ being simplicial. This concludes the case $\phi (e_3) \ne e_1$ and the entire proof. $\square$

The following strengthens Lemma 44 by slightly relaxing the preconditions.

Proposition 47

Let $P$ be a simplicial, terminal, and reflexive $d$-polytope with exactly $3d-2$ vertices such that $v_P=\mathbf 0$. Suppose that $P$ has a (special) facet $F$ with $\eta ^F=(d,d-1,d-2,1)$ and there is a vertex $v$ of $F$ such that ${{\mathrm{opp}}}(F,v) \not \in V(F,0)$. Then $P$ is a (possibly skew) bipyramid over some simplicial, terminal, and reflexive polytope of dimension $d-1$ with $3d-4$ vertices.

Proof

If ${{\mathrm{opp}}}(F,v) \in V(F,-2)$ for some $v\in \mathrm{Vert }(F)$ we can apply Lemma 44 to prove the claim. So we may assume that there exists a vertex $v$ in $F$ with ${{\mathrm{opp}}}(F,v) \in V(F,-1)$. By Proposition 33 we may assume $v=e_1$ and (using $\phi \, {:}{=}\,\phi ^F$)

$$\begin{aligned} V(F,0)&= \, \{\phi (e_2)-e_2,\, \phi (e_3)-e_3,\, \ldots , \phi (e_d)-e_d \},\\ V(F,-1)&\subseteq \, \{-e_1, \ldots , -e_d\}\;\cup \; \left\{ -2e_1-e_r +e_s+e_t\,\right. \left| \,r,s,t \in [d] \text { p.d.},\, r\ne 1\right\} . \end{aligned}$$

By our assumption the vertex $y\,{:}{=} {{\mathrm{opp}}}(F,e_1)$ is at level $-1$ with respect to $F$. We see that it is one of the points

$$\begin{aligned} -e_1, \quad -e_1-e_r+e_s, \quad \text {or} \quad -2e_1 - e_r + e_s + e_t, \end{aligned}$$

(14)

for pairwise distinct $r,s,t$ and $r\ne 1$. So $u_{F^{(1)}}=\mathbf 1-2e_1$ for the first two possibilities, $u_{F^{(1)}}=\mathbf 1-e_1$ for the third, and $u_{F^{(j)}}=\mathbf 1-e_j$ for any $j\ge 2$.

Let $z$ be the unique vertex in $V(F,-2)$. If $z_i=\langle u_{F,e_i}, z \rangle$ is positive for some $i$, then $z\in V(\mathrm{N }(F,e_i),-3)$. But $\mathrm{N }(F,e_i)$ is special, so this contradicts Proposition 43. We know that $z\ne -2e_i$ for all $i$ as the vertices must be primitive lattice vectors. Hence, $z=-e_\alpha -e_\beta$ for distinct $\alpha ,\beta \in [d]$. We consider all possible forms of $y={{\mathrm{opp}}}(F,e_1)$ according to (14) separately.

$\begin{array}{|l|}\hline {\hbox {Let}\; y=-e_1.}\\ \hline \end{array}$ Then we have $u_{F^{(1)}}=\mathbf 1-2e_1$, and this implies that no other vertex in $V(F,-1)$ can have a negative first coefficient. So, up to relabeling, $V(F,-1)=\{-e_1,-e_2,\ldots , -e_{d-2}\}$. Choose $k \in \{ 1,d-1,d \}\setminus \{ \alpha ,\beta \}$. The fact that $v_P=\mathbf 0$ implies that $e_k\not \in {{\mathrm{im}}}\phi$. Hence, $P$ is a (possibly skew) bipyramid with apices $e_k$ and ${{\mathrm{opp}}}(F,e_k)$.

$\begin{array}{|l|}\hline {\hbox {Let} \; y=-e_1-e_r+e_s.}\\ \hline \end{array}$ We may assume that $r=2$ and $s=3$. By Lemma 46 the vertices $e_1$ and $y={{\mathrm{opp}}}(F,e_1)$ are distant, and thus Lemma 18 gives us that $e_1+y=-e_2+e_3$ is a vertex of $P$. This means that $\phi (e_2) = e_3$. $u_{F^{(1)}}=\mathbf 1-2e_1$ implies that no other vertex in $V(F,-1)$ can have a negative first coefficient. Hence, there are distinct $i,j \in [d]\setminus \{ 1 \}$ such that

$$\begin{aligned} V(F,-1)\ = \ \left\{ -e_k \,\right. \left| \, k \in [d] \,\text { with }\, k\ne 1,i,j \right\} \cup \{ y \}. \end{aligned}$$

If $z_1=0$ then $v_P=\mathbf 0$ implies $e_1\not \in {{\mathrm{im}}}\phi$. In this case $P$ is a skew bipyramid over the $(d{-}1)$-polytope $Q=\{x\in P\,|\,x_1=0\}$ with apices $e_1$ and $-e_1-e_2+e_3$.

It remains to consider that case that $\alpha =1$ and $e_1 \in {{\mathrm{im}}}\phi$. This yields $\phi (e_\beta )\ne e_1$ as otherwise $-e_\beta =\frac{1}{2} ( z + (\phi (e_\beta )-e_\beta ) )$ is a non-zero lattice point in $P$ which is not a vertex. This way we obtain

$$\begin{aligned} \mathbf{0}&= v_P \nonumber \\&= \sum _{k=1}^d e_k \, + \, \sum _{k=2}^d(\phi (e_k)-e_k) \, - \, \sum _{k\ne 1,i,j} e_k \, + \, y \, + \, z \nonumber \\&= \sum _{k=2}^d(\phi (e_k)-e_k) \, + \, e_i + e_j - e_\beta - e_1 - e_2 + e_3 \nonumber \\&= \sum _{k=4}^d(\phi (e_k)-e_k) \, + \, \phi (e_3) + e_i + e_j - e_\beta - e_1 - 2e_2 + e_3, \end{aligned}$$

(15)

where the last step uses $\phi (e_2)=e_3$. Now the vanishing of the third coordinate on the right hand side of (15) forces $\beta =3$. This equation then simplifies to

$$\begin{aligned} \mathbf 0 = \sum _{k=3}^d \phi (e_k) \, + \, e_i + e_j \,-\, \sum _{k\ne 3}e_k \,-\, e_2. \end{aligned}$$

(16)

Note that it is not possible for $i$ or $j$ to be equal to $3$, otherwise the third coordinate of the right hand side is strictly positive. Vanishing of the $i$-th coordinate on the right hand side of (16) implies the following: If $i \ne 2$ then $i\not \in {{\mathrm{im}}}\phi$. In this case $P$ is a skew bipyramid with apices $e_i$ and $\phi (e_i)-e_i$. The same reasoning holds for $j$. Since $i$ and $j$ are distinct at least one of them must differ from $2$. So this case leads to a skew bipyramid.

$\begin{array}{|l|}\hline {\hbox {Let} \; y=-2e_1-e_r+e_s+e_t.}\\ \hline \end{array}$ We will show that this case cannot occur. The situation is sketched in Fig. 5. The facet $F^{(1)}\,{:}{=}\,\mathrm{N }(F,e_1)$ has standard facet normal $u_{F^{(1)}} = \mathbf 1 -e_1$.

Fig. 5

Facet $F$ and neighboring facets for $y=-2e_1-e_r+e_s+e_t$

Assume first that $\phi (e_r)\ne e_1$. Then ${{\mathrm{opp}}}(F,e_r)=e_i-e_r$ for some $i\ne 1,r$, and

$$\begin{aligned} \langle u_{F^{(1)}}, {{\mathrm{opp}}}(F,e_r) \rangle \ = \ \langle \mathbf 1 - e_1, e_i-e_r \rangle \ = \ 1-1 \ = \ 0 . \end{aligned}$$

(17)

Furthermore, $u_{F^{(1)},e_r} = e_r - \frac{1}{2} e_1$, and so

$$\begin{aligned} \langle u_{F^{(1)},e_r}, {{\mathrm{opp}}}(F,e_r) \rangle \ = \ \big \langle e_r-\frac{1}{2}e_1,e_i-e_r \big \rangle \ = \ -1 . \end{aligned}$$

Since $\langle u_{F^{(1)},e_r}, {{\mathrm{opp}}}(F,e_r) \rangle$ is negative, Proposition 20(ii) tells us that ${{\mathrm{opp}}}(F,e_r)$ is the opposite vertex of $e_r$ with respect to $F^{(1)}$, so ${{\mathrm{opp}}}(F^{(1)},e_r) = {{\mathrm{opp}}}(F,e_r)$. Using this we conclude that $\langle 2\cdot \mathbf 1 - e_1-2e_r, x\rangle \le 2$ defines the facet of $\mathrm{N }(F^{(1)},e_r)$. This contradicts the assumption that $P$ is reflexive. Hence, in the following we can assume that $\phi (e_r)=e_1$.

The facet $F^{(r)}\, {:}{=}\mathrm{N }(F,e_r)$ has vertices $\{e_i\,|\,i\ne r\}$ and $e_1-e_r$, and facet normal $u_{F^{(r)}} = \mathbf 1 - e_r$. We want to show that for all vertices $x\ne e_1$ on $F^{(r)}$ the opposite vertex ${{\mathrm{opp}}}(F^{(r)},x)$ does not coincide with $y$. Trivially we have ${{\mathrm{opp}}}(F^{(r)},{{\mathrm{opp}}}(F,e_r)) = e_r\ne y$. It remains to check the vertices $e_i$ for $i\ne r$. The dual basis is

$$\begin{aligned} u_{F^{(r)},{{\mathrm{opp}}}(F,e_r)}\, = \ -e_r\,, u_{F^{(r)},e_1}\ =\ e_1+e_r\,, u_{F^{(r)},e_i}\ =\ e_i\quad \text { for } i\ne 1,r. \end{aligned}$$

so $\langle u_{F^{(r)},e_i}, -2e_1-e_r+e_s+e_t \rangle$ is negative if and only if $i=1$. Observe that $y$ is on level $0$ with respect to $F^{(r)}$. In view of Proposition 20(ii) we obtain that ${{\mathrm{opp}}}(F^{(r)},e_i)\ne y$ for $i\ne 1,r$.

Now we can apply Proposition 20(iii) which tells us that the vertices $e_1$ and ${{\mathrm{opp}}}(F,e_1)$ are distant, and according to Lemma 18 the point $x\, {:}{=}e_1+{{\mathrm{opp}}}(F,e_1)=-e_1 -e_r + e_s + e_t$ is a vertex of $P$. Clearly, $x$ lies on level $0$ with respect to $F$ which forces $1\in \{s,t\}$ or $r\in \{s,t\}$. However, both cases are excluded due to our initial assumption on $y$ in this case. Hence, this last case does not occur. $\square$

Example 48

As discussed in Example 45 the facet $H$ of the polytope $B$ from Example 14 has $\eta$-vector $(4,3,2,1)$, and the opposite vertex of $e_3$ is on level $-2$ with respect to the facet $H$. Hence, $B$ is a bipyramid.

The following result is dealing with $\eta ^{F}=(d,d,d-4,2)$ and reduces it to one case we already dealt with so far.

Lemma 49

Let $P$ be a $d$-dimensional simplicial, terminal, and reflexive polytope with exactly $3d-2$ vertices and some special facet $F$ with $\eta ^F = (d,d, d-4, 2)$. Then $P$ is lattice equivalent to a skew bipyramid over a $(d{-}1)$-dimensional smooth Fano polytope with $3d-4$ vertices, or there exists another facet $G$ with $\eta ^G = (d,d-1,d-2, 1)$ and one vertex $w\in G$ with ${{\mathrm{opp}}}(G,w) \not \in V(G,0)$.

The two cases in the conclusion are not necessarily mutually exclusive.

Proof

Let $\phi \, {:}{=}\,\phi ^F$. Since $\eta ^F_0 = d$ we can assume $F = {{\mathrm{conv}}}\{ e_1,e_2,\ldots , e_d \}$ by Proposition 33. Moreover, $V(F,0)=\{\phi (e_i)-e_i\,|\,i\in [d]\}$ and up to relabeling we can assume that $V(F,-1)=\{-e_5,-e_6, \ldots , -e_d\}$. Further, if $-e_i$ is a vertex then $\phi (\phi (e_i))=e_i$, which implies that ${{\mathrm{im}}}(\phi )$ contains the vertices $\{e_5,e_6,\ldots ,e_d\}$.

Let $x$ and $y$ be the two vertices in $V(F,-2)$. Then

$$\begin{aligned} 0\ = \ v_P\ = \ x+y \,+\, \sum _{i=1}^d \phi (e_i) \,-\, \sum _{i=5}^d e_i\,, \end{aligned}$$

and hence $x+y=-e_h-e_i-e_j-e_k$ for some not necessarily distinct $h,i,j,k\in [d]$. The equation above also shows that ${{\mathrm{im}}}\phi = \{ e_h, e_i,e_j,e_k \} \cup \{ e_5, e_6,\ldots , e_d \}$.

We want to show that all coordinates of $x$ and $y$ are non-positive. Suppose that $x_a>0$ for some $a\in [d]$. Consider the neighboring facet $F'\, {:}{=}\,\mathrm{N }(F,e_a)$. Then $x$ lies on level $-3$ or below with respect to $F'$. However, as $v_P=\mathbf 0$, the facet $F'$ is special, too, and the case $\eta ^{F'}_\ell >0$ for $\ell \le -3$ is excluded by Proposition 43. The same argument works for the vertex $y$. Once more we distinguish two cases.

$\begin{array}{|l|}\hline {\hbox {Let} \;\{ h,i,j,k \}\ne \{1,2,3,4\}.}\\ \hline \end{array}$ Without loss of generality we may assume that $h,i,j,k$ are all distinct from $1$. We see that $e_1$ is not contained in ${{\mathrm{im}}}(\phi )$. This means that $P$ is a skew bipyramid with apices $e_1$ and $\phi (e_1)-e_1$.

$\begin{array}{|l|}\hline {\hbox {Let} \;\{ h,i,j,k \}=\{1,2,3,4\}.}\\ \hline \end{array}$ Without loss of generality, $x=-e_1-e_2$ and $y=-e_3-e_4$. In this case the map $\phi$ is bijective since ${{\mathrm{im}}}\phi = \{ e_1, e_2, \ldots , e_d \}$. We will reduce this to another case that we will have to look into anyway. This way we save a further distinction of cases. We look at the facet $G\, {:}{=}\,\mathrm{N }(F,e_1)$ with facet normal vector $u_{G} = \mathbf 1-e_1$. Let $e_r$ be the inverse image of $e_1$ with respect to the bijection $\phi$. We obtain

$$\begin{aligned} V(G, 1)&= \left\{ e_i\,\right. \left| \,2\le i \le d\right\} \cup \{ \phi (e_1)-e_1 \},\\ V(G, 0)&= \left\{ \phi (e_i)-e_i\,\right. \left| \,i\in [d]\setminus \{ 1,r \}\right\} \cup \{ e_1 \},\\ V(G, -1)&= \left\{ -e_i\,\right. \left| \,\,\right\} {5\le i \le d} \cup \{ \phi (e_r)-e_r, -e_1-e_2 \},\\ V(G, -2)&= \{ -e_3-e_4 \}. \end{aligned}$$

Therefore $\eta ^{G} = (d,d-1,d-2,1)$. For the vertex $z\, {:}{=}\,{{\mathrm{opp}}}(G,e_r)$ we have the inequality $\langle u_{G,e_r},z\rangle <0$ by Proposition 20(ii). We will show that $z$ is not contained in $V(G,0)$. To this end we compute

$$\begin{aligned} u_{G,e_r} \ = \ {\left\{ \begin{array}{ll} e_1 + e_r &{} \text {if } \phi (e_1)=e_r,\\ e_r &{} \text {otherwise}. \end{array}\right. } \end{aligned}$$

Either way, from looking at the above list of vertices of $P$ we see that every vertex $v\in V(G,0)$ satisfies $\langle u_{G,e_r}, v\rangle \ge 0$. We conclude that $z$ is not on level zero with respect to $G$, and we may take $w\, {:}{=}\, e_r$ to prove our claim. $\square$

Lemma 50

Let $P$ be a simplicial, terminal, and reflexive $d$-polytope with exactly $3d-2$ vertices such that $v_P=\mathbf 0$. Suppose that $P$ has a (special) facet $F$ with $\eta ^F=(d,d-1,d-2,1)$ and for every vertex $v$ of $F$ we have ${{\mathrm{opp}}}(F,v) \in V(F,0)$. Then $P$ is a (possibly skew) bipyramid over some simplicial, terminal, and reflexive polytope of dimension $d-1$ with $3d-4$ vertices.

Proof

By Proposition 33(ii) we may assume that $F={{\mathrm{conv}}}\{e_1,e_2, \ldots , e_d\}$ and

$$\begin{aligned} V(F,0)&= \, \{-e_1-e_2+e_a+e_b,\, \phi (e_3)-e_3,\, \ldots ,\, \phi (e_d)-e_d\}, \nonumber \\ V(F,-1)&\subseteq \, \{-e_1,\, -e_2,\, \ldots ,\, -e_d\} \;\cup \; \left\{ -e_1-e_2 + e_k\,\right. \left| \,k\in [d]\right\} \end{aligned}$$

(18)

for $a, b \in [d] \setminus \{ 1,2 \}$ not necessarily distinct.

Let $z=\sum _{i\ge 1}\mu _ie_i$ be the unique vertex at level $-2$ with respect to $F$. If $\mu _i=\langle u_{F,e_i}, z \rangle$ is positive for some $i$, then $z\in V(\mathrm{N }(F,e_i),-3)$. But $\mathrm{N }(F,e_i)$ is special, so this contradicts Proposition 43. Hence, $\mu _i\le 0$ for all $i$ and $z=-e_r-e_s$ for some indices $r\ne s$. Furthermore, if $-e_1-e_2+e_k\in P$ for some $k\ne r,s$ we get that this vertex as well as $z$ would lie on level $-2$ with respect to the facet $\mathrm{N }(F,e_k)$. So this adjacent facet must have $\eta$-vector $(d,d,d-4,2)$ which is already dealt with Lemma 49. This implies

$$\begin{aligned} V(F,-1) \ \subset \ \{-e_1,-e_2, \ldots , -e_d\}\;\cup \;\{-e_1-e_2+e_r, -e_1-e_2+e_s\}. \end{aligned}$$

(19)

Let $H\, {:}{=}\,\mathrm{N }(F,e_a)$. The vertex $e_a$ is good due to our assumption every vertex of $F$ is good, and so $u_{H}=\mathbf 1-e_a$. We distinguish between $a=b$ and $a\ne b$.

$\begin{array}{|l|}\hline {\hbox {Let} \;a=b.}\\ \hline \end{array}$ Then $x={{\mathrm{opp}}}(F,e_1)={{\mathrm{opp}}}(F,e_2)=-e_1-e_2+2e_a$ and we compute $\langle u_H,x\rangle =\langle \mathbf 1-e_a,x\rangle =-2$. Either $x$ is the only vertex in $V(H,-2)$ and hence $\eta ^H = (d,d-1,d-2,1)$ or there is another vertex in $V(H,-2)$ besides $x$ which would result in $\eta ^H = (d,d,d-4,2)$, but this case is already captured in Lemma 49. So we can assume that $x$ is the only vertex in $V(H,-2)$.

Up to exchanging $e_1$ and $e_2$, we can assume that $\phi (e_a)\ne e_1$. We consider the vertex $y\,{:}{=}\,{{\mathrm{opp}}}(H,e_1)$. The case $y \not \in V(H,0)$ is already covered in Proposition 47. So we can assume $y$ is in $V(H,0)$. As $u_{H,e_1}=e_1$, this implies that $\langle u_{H,e_1}, y\rangle < 0$, that is, in the basis defined by $H$, the $e_1$-coordinate of $y$ must be negative. As $\phi (e_a)\ne e_1$ the $e_1$-coordinate of $y$ in the basis of $H$ coincides with $y_1$, which is the $e_1$-coordinate in the basis of $F$. We can check which vertices or vertex candidates have a negative first coordinate. These turn out to be $x$, and $-e_1, -e_1-e_2+e_r$, and $-e_1-e_2+e_s$, if they exist. However, none of these lies on level zero. Hence, a vertex $y$ with these properties does not exist in $V(F,0)$. This finishes the case that $a=b$.

$\begin{array}{|l|}\hline {\hbox {Let} \;a\ne b.}\\ \hline \end{array}$ Then our case distinction has a further ramification.

• (i) Let $\{ a,b \} \ne \{ r,s \}$. Without loss of generality we can assume that $a \not \in \{ r,s \}$. We define $F^{(a)}\, {:}{=}\, \mathrm{N }(F,e_a)$. Since $\langle u_{F,e_a}, -e_r-e_s \rangle = 0$ we know that $-e_r-e_s$ is contained in $V(F^{(a)}, -2)$. In particular, $\eta ^{F^{(a)}}_{-2}$ does not vanish and hence the $\eta$-vector of $F^{(a)}$ reads $(d,d-1,d-2,1)$ or $(d,d,d-4,2)$. The latter being already discussed in Lemma 49 so we are left with the first $\eta$-vector. This further implies that $\langle u_{F,e_a}, x \rangle \le 0$ for all $x\in V(F,-1)$. All vertices in $F$ are good, so Lemma 31 tells us that there can only be one vertex $x\in V(F,-1)$ with $\langle u_{F,e_a}, x \rangle = -1$. Due to the bounds obtained from Lemma 16 the only possible vertex in $V(F,-1)$ which has a non-positive scalar product with $u_{F,e_a}$ is $-e_a$. Summing up all vertices $y$ of $P$ with $\langle u_{F,e_a}, y \rangle \ne 0$ implies that $e_a$ cannot be contained in the image of $\phi$. Hence,

  $$\begin{aligned} V(F^{(a)},0) = \ \left\{ \phi (e_i)-e_i\,\right. \left| \,i \in [d] \setminus \{ 1,2,a \}\right\} \cup \{ \pm e_a \} . \end{aligned}$$

  Up to exchanging $e_1$ and $e_2$ we may assume that $\phi (e_a)\ne e_1$. Thus $u_{F^{(a)}, e_1} = e_1$, which implies $\langle u_{F^{(a)}, e_1}, x \rangle \ge 0$ for all $x\in V(F^{(a)},0)$. However, this excludes that ${{\mathrm{opp}}}(F^{(a)},e_1)$ is contained in $V(F^{(a)},0)$. Which is the case already considered in Proposition 47.

• (ii) Let $\{ a,b \} = \{r,s\}$. Then $x=-e_1-e_2 +e_r+e_s$ is the vertex which is opposite both to $e_1$ and $e_2$ with respect to $F$. From the argument in the case $a=b$ we learn that if $-e_1-e_2 +e_r$ or $-e_1-e_2 +e_s$ were vertices of $P$ then the facet $F^{(r)}\, {:}{=}\,\mathrm{N }(F,e_r)$ or the facet $F^{(s)}\,{:}{=}\,\mathrm{N }(F,e_s)$ would contain a vertex such that its opposite does not lie on level zero with respect to $F^{(r)}$ or $F^{(s)}$. This vertex would either be $e_1$ or $e_2$. Again this case is already captured in Proposition 47. Therefore, neither $-e_1-e_2 +e_r$ nor $-e_1-e_2 +e_s$ is a vertex of $P$. By (19) we have that $V(F,-1)\subset \left\{ -e_i\,\right. \left| \,i\in [d]\right\}$. Using the generic forms of all vertices given in (18) and (19) we conclude that there is no $v\in \mathrm{Vert }(P)$ such that $x+v$ is again a vertex. Hence, by Lemma 18, no vertex of $P$ is distant to $x$. In particular, there is a facet $G$ which contains both $x=-e_1-e_2+e_r+e_s$ and $z=-e_r -e_s$. This implies

  $$\begin{aligned} 2 = \ \langle u_G, -e_1-e_2+e_r+e_s \rangle + \langle u_G, -e_r-e_s \rangle \ = \ \langle u_G, -e_1 -e_2 \rangle . \end{aligned}$$

  However, this inequality says that if $-e_1$ and $-e_2$ are vertices of $P$ then they, too, are contained in $G$. The four points $-e_1,-e_2,x,z$ are linearly dependent, hence the facet $G$ cannot be a simplex. This is impossible. We may thus assume that $-e_1$ is not a vertex of $P$. The vertices of $P$ with a non-vanishing first coordinate comprise $e_1, -e_1-e_2+e_r+e_s$ and possibly $e_1-e_i$ for some $i\ge 3$. Since, however, the vertex sum $v_P$ vanishes the sum of the first coordinates of all vertices vanishes. This excludes that $e_1-e_i$ is a vertex of $P$ for any $i\ge 3$; this is to say that $e_1$ is not contained in the image of $\phi$. Suppose that $\phi (e_r)=e_s$. Then we have

  $$\begin{aligned} \frac{1}{2}(\phi (e_r)-e_r+z) \ = \ \frac{1}{2}(e_s - e_r - e_r - e_s) \ = \ -e_r . \end{aligned}$$

  In view of the fact, however, that both $\phi (e_r)-e_r$ and $z$ are vertices of $P$ this is a contradiction to the terminality of $P$. So $\phi (e_r)\ne e_s$ and, by symmetry, also $\phi (e_s)\ne e_r$. The standard normal vector of the facet $F^{(r)}$ reads $\mathbf 1-e_r$, and thus the vertex $\phi (e_s)-e_s$ lies on level zero with respect to $F^{(r)}$. Each such vertex is opposite to some vertex in $F^{(r)}$, and we infer that ${{\mathrm{opp}}}(F^{(r)},e_s)={{\mathrm{opp}}}(F,e_s)=\phi (e_s)-e_s$. This is to say that the vertex $e_s$ is good with respect to $F^{(r)}$. Up to exchanging $e_r$ and $e_s$ we may assume that $e_2 \ne \phi (e_r)$. We claim that $\phi (e_r)$ is also good with respect to $F^{(r)}$. To see this we consider two cases. Either $\phi (\phi (e_r)) = e_r$ or $\phi (\phi (e_r)) \ne e_r$. In the first case, $-e_r$ must be a vertex of $P$, and $-e_r = (\phi (e_r) - e_r) - \phi (e_r)$ lies on level zero with respect to $F^{(r)}$. This yields ${{\mathrm{opp}}}(F^{(r)},\phi (e_r))=-e_r$, and $\phi (e_r)$ is good with respect to $F^{(r)}$. It remains to consider the case where $\phi (\phi (e_r))\ne e_r$. Then ${{\mathrm{opp}}}(F,\phi (e_r)) = {{\mathrm{opp}}}(F^{(r)},\phi (e_r))\in V(F,0)$ which makes $\phi (e_r)$ good with respect to $F^{(r)}$. The vertex $-e_r-e_s = (\phi (e_r)-e_r) - \phi (e_r) -e_s$ now satisfies

  $$\begin{aligned} \langle u_{F^{(r)}, \phi (e_r)}, -e_r-e_s \rangle \ = \ -1 \ = \ \langle u_{F^{(r)}, e_s}, -e_r-e_s \rangle . \end{aligned}$$

  The final contradiction now comes from Lemma 31 since we showed that both $e_s$ and $\phi (e_r)$ are good with respect to $F^{(r)}$ and ${{\mathrm{opp}}}(F^{(r)},e_s) = \phi (e_s)-e_s \ne {{\mathrm{opp}}}(F^{(r)},\phi (e_r))$. $\square$

The following compiles the results of this section into one concise statement.

Theorem 51

Let $P$ be a $d$-dimensional simplicial, terminal, and reflexive polytope with exactly $3d-2$ vertices and $v_P=\mathbf 0$. Then $P$ is lattice equivalent to one of the following:

• (i) a (possibly skew) bipyramid over

  • either $P_5 \oplus P_6^{\oplus \frac{d-3}{2}}$

  • or a (possibly skew) bipyramid over $P_6^{\oplus \frac{d-2}{2}}$,

• (ii) $\mathrm{DP }(4) \oplus P_6^{\oplus \frac{d}{2} - 2}$.

Proof

According to Table 1 the a priori feasible $\eta$-vectors are $(d,d,d-3,0,1), (d,d-2,d), (d,d,d-4,2)$, or $(d,d-1,d-2,1)$.

The first case is actually excluded by Proposition 43. If the $\eta$-vector of each facet of $P$ equals $(d,d-2,d)$, then $P$ is centrally symmetric by Proposition 41 and thus classified by Corollary 42. This, in particular, comprises the polytope $\mathrm{DP }(4) \oplus P_6^{\oplus \frac{d}{2} - 2}$. Therefore, our goal is to show that in all remaining cases $P$ is a possibly skew bipyramid over a suitable base polytope.

We may assume that $P$ has at least one facet, $F$, with $\eta ^F=(d,d,d-4,2)$ or $\eta ^F=(d,d-1,d-2,1)$. Recall that all facets are special as $v_P=\mathbf 0$.

Let us consider the case where $\eta ^F=(d,d-1,d-2,1)$. Then our case distinction further ramifies depending on where the vertices opposite to the vertices of $F$ are located. Let

$$\begin{aligned} S \ = \ \left\{ {{\mathrm{opp}}}(F,v)\,\right. \left| \,v\in F\right\} \,. \end{aligned}$$

Either there is a vertex in $S$ which lies at level $-1$ or $-2$ with respect to $F$. Then we call $F$ of type A, and Proposition 47 tells us that $P$ is a proper or skew bipyramid. Or all vertices in $S$ are at level zero. We will postpone the latter case, which we call type B.

Suppose now that $\eta ^F=(d,d,d-4,2)$. Then Lemma 49 shows that either $P$ is possibly skew bipyramid, or there is another facet whose $\eta$-vector reads $(d,d-1,d-2,1)$, and which is of type A. So this is already resolved.

It remains to consider $\eta ^F=(d,d-1,d-2,1)$ of type B. Then Lemma 50 finally shows that $P$ again must be a proper or skew bipyramid. Our argument is based on the previous cases. $\square$